1. Introduction
The formalism of quantum physics has been developed during the first decades of the 20th century. It describes a physical system as an element 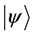 of some appropriate Hilbert space
of some appropriate Hilbert space 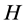 and physical, observable quantities as eigenvalues
and physical, observable quantities as eigenvalues  in the spectrum
in the spectrum 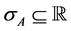 of self-adjoint operators
of self-adjoint operators 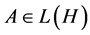 on that Hilbert space. The eigenvalue-eigenstate postulate says that, whenever a system is found to have a value
on that Hilbert space. The eigenvalue-eigenstate postulate says that, whenever a system is found to have a value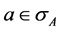 , then it is in the corresponding eigenstate
, then it is in the corresponding eigenstate 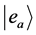 of
of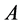 . Inversely, if a system
. Inversely, if a system 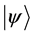 is represented in the eigenbasis,
is represented in the eigenbasis, 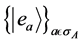 , of
, of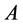 ,
,  , then the system is experimentally found to have eigenvalue
, then the system is experimentally found to have eigenvalue 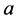 with probability
with probability
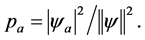 (1)
(1)
This is the Born-rule [1] . The Born-rule together with the eigenvalue-eigens- tate link constitutes the measurement postulate. No violation of the Born-rule has ever been discovered experimentally. The measurement postulate is incompatible with a further postulate of quantum mechanics, namely the unitary evolution of the quantum state. Ever since the establishment of the theory there have been different interpretations and extensions of quantum physics in order to solve this incompatibility, known as the “measurement problem”.
2. Some Formalism
Given the resolution of a state  in the eigenbasis
in the eigenbasis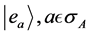 , of an operator
, of an operator ,
, ![]() , we can form the corresponding density matrix
, we can form the corresponding density matrix ![]() with matrix-entries
with matrix-entries![]() . This matrix is a self-adjoint operator, a projection operator in this case, satisfying
. This matrix is a self-adjoint operator, a projection operator in this case, satisfying![]() . If
. If ![]() is normalized,
is normalized, ![]() , then so is the trace of
, then so is the trace of![]() ,
, ![]() , and the diagonal matrix-elements of
, and the diagonal matrix-elements of ![]() happen to correspond to the numerical values in the Born probabilities
happen to correspond to the numerical values in the Born probabilities![]() . By the correspondence,
. By the correspondence, ![]() , there is an alternative formulation of the postulates of traditional quantum physics in terms of density operators. If a density operator satisfies
, there is an alternative formulation of the postulates of traditional quantum physics in terms of density operators. If a density operator satisfies![]() , i.e. is a projector, we say that
, i.e. is a projector, we say that ![]() is pure. Density operators can be thought to incorporate the known information about a state and this allows a generalization. Given a set
is pure. Density operators can be thought to incorporate the known information about a state and this allows a generalization. Given a set ![]() of pure density operators and a set of probability weights
of pure density operators and a set of probability weights![]() ,
, ![]() , we can form a new density operator
, we can form a new density operator
![]() (2)
(2)
We say that the operator ![]() in (2) is a mixed state. Mixed states
in (2) is a mixed state. Mixed states ![]() are formally self-adjoint operators with
are formally self-adjoint operators with ![]() but no projectors, so
but no projectors, so![]() . The interpretation of mixed states is entirely classical in the sense that the probabilities
. The interpretation of mixed states is entirely classical in the sense that the probabilities ![]() reflect a lack of knowledge and hence belief in the likelihood of elements of a set of possible preparations, done in a lab for instance. There is a theorem due to Gleason [8] , which basically says that the trace-function
reflect a lack of knowledge and hence belief in the likelihood of elements of a set of possible preparations, done in a lab for instance. There is a theorem due to Gleason [8] , which basically says that the trace-function
![]() is the unique probability measure, which is faithful to the postulates of quantum physics on Hilbert space1. Gleason’s theorem tells us that we are looking at the right probabilities. But it is per se not helpful to better understand the nature of the Born-probabilities.
is the unique probability measure, which is faithful to the postulates of quantum physics on Hilbert space1. Gleason’s theorem tells us that we are looking at the right probabilities. But it is per se not helpful to better understand the nature of the Born-probabilities.
Measurement
Assume there is a density matrix ![]() and basis (eigen)-states
and basis (eigen)-states![]() , corresponding to some self-adjoint operator
, corresponding to some self-adjoint operator![]() . Assume in addition that there is an additional system
. Assume in addition that there is an additional system ![]() with orthonormal basis states
with orthonormal basis states![]() , which we assume originally to be in the base state
, which we assume originally to be in the base state![]() . A measurement of
. A measurement of ![]() by the probe
by the probe ![]() is an operation
is an operation ![]() on the joint system
on the joint system ![]()
![]() (3)
(3)
where ![]() is unitary
is unitary ![]() 2. A general unitary transformation on a tensor-product, expressed in the respective bases, can be written as a matrix
2. A general unitary transformation on a tensor-product, expressed in the respective bases, can be written as a matrix
![]() (4)
(4)
where the operators ![]() are given by
are given by![]() . We denote the diagonal sub-block
. We denote the diagonal sub-block ![]() simply by
simply by![]() . Since
. Since ![]() is unitary, we have
is unitary, we have
![]() (5)
(5)
Conversely, we can choose any set of operators ![]() satisfying the resolution of the identity-condition (5) to define a measurement on an initial joint state
satisfying the resolution of the identity-condition (5) to define a measurement on an initial joint state![]() . We now have the necessary elements in place to give the main argument.
. We now have the necessary elements in place to give the main argument.
3. The Born-Rule
Assume there is a quantum system ![]() in a, not necessarily normalized, pure state
in a, not necessarily normalized, pure state ![]() with representation
with representation![]() , and corresponding density matrix
, and corresponding density matrix ![]() with matrix elements
with matrix elements
![]() . We further assume all the postulates of traditional quantum physics as above, except the Born-rule, and ask ourselves where the probabilities come from.
. We further assume all the postulates of traditional quantum physics as above, except the Born-rule, and ask ourselves where the probabilities come from.
Assume there is a second system ![]() with basis
with basis ![]() and an observer who would like to know in what state
and an observer who would like to know in what state ![]() the system
the system ![]() is in, by making an appropriate measurement
is in, by making an appropriate measurement ![]() on the joint system
on the joint system![]() . If that is possible in the first place, then, having no additional knowledge, the observer does a priori not know in what state
. If that is possible in the first place, then, having no additional knowledge, the observer does a priori not know in what state![]() , the probe will be after the measurement and before observation.
, the probe will be after the measurement and before observation.
![]() 3. The probe
3. The probe ![]() can be chosen appropriately coarse- grained4 such that
can be chosen appropriately coarse- grained4 such that ![]() We now introduce probabilities by Laplace’s principle of indifference. The observer is after the measurement and before observation in a situation where, by lack of further information, she will a priori attribute to each outcome
We now introduce probabilities by Laplace’s principle of indifference. The observer is after the measurement and before observation in a situation where, by lack of further information, she will a priori attribute to each outcome ![]() equal probability
equal probability
![]() . This attribution is equivalent to maximizing the entropy function
. This attribution is equivalent to maximizing the entropy function![]() . The observer can therefore write down in the spirit of (2) an average of outcomes
. The observer can therefore write down in the spirit of (2) an average of outcomes
![]() (6)
(6)
For our purpose we now chose the operators ![]() to be the scaled projectors
to be the scaled projectors ![]() to the basis-states
to the basis-states![]() . Note that we have replaced the simple-index
. Note that we have replaced the simple-index ![]() by the double-index
by the double-index![]() . This choice is consistent with the demands of a measurement, since the
. This choice is consistent with the demands of a measurement, since the ![]() satisfy (5)
satisfy (5)
![]() (7)
(7)
Therefore we can write (6) in the following form
![]() (8)
(8)
Comparing Equation (8) with Equation (2), we see that ![]() can be viewed as a mixed state with probabilities
can be viewed as a mixed state with probabilities
![]() (9)
(9)
which is the Born-rule.
4. Conclusions
We have in the above derivation not made use of any specific interpretation of quantum mechanics, but relied on two basic assumptions only. The first one is the formalism of density operators and generalized measurement with classical or epistemic probabilities arising in mixed states (2). The second one is Laplace’s principle of indifference in order to introduce the concept of probabilities and to assign concrete probability-values![]() , to the mixed state in (6). This is the important step, which helps to avoid the kind of tautological argument based on the reduced density matrix and Gleason’s theorem. It bases on a kind of symmetry of the probe states
, to the mixed state in (6). This is the important step, which helps to avoid the kind of tautological argument based on the reduced density matrix and Gleason’s theorem. It bases on a kind of symmetry of the probe states![]() , due to a lack of knowledge before observation.
, due to a lack of knowledge before observation.
We have found that, given any not necessarily normalized pure state, it is possible to define an observer with an appropriately coarse-grained probe-system5 who, by lack of further knowledge, will assign exactly the Born-probabilities, as classical probabilities in the sense of (2), to finding the system in one of the basis-states, after the measurement and before observation. In other words, there is the possibility to interpret the normalized amplitudes of an arbitrary state ![]() as epistemic probabilities for different possible measurement outcomes.
as epistemic probabilities for different possible measurement outcomes.
If a quantum state ![]() is given to us a priori, then it seems that the Born- probabilities are objectively given with it and there might be a reluctance to embrace Laplace’s principle as fundamental [9] . It seems to us that we can accept the principle as deeply rooted in our intuition and therefore to be a first principle. Authors, concerned with the many worlds interpretation in [6] [7] for instance, try to give more objective physical justifications for Laplace’s principle, mainly by describing the symmetry, which it bases on, in more physical terms. We are not sure that these ideas are really more fundamental or whether they are not the same intuition vested in different garments. We should in all this always remember that quantum states are practically given to us by making preparations, i.e. by correlating them with other systems in laboratories. It is a wonderful fact, however, that the Born-probabilities are confirmed by the corresponding frequencies, if repeated experiments are being done. This would probably not be further impressive, if quantum states would just be results of gathering measurement information. But they can also arise from an initial state by Schrödinger evolution. We at least can say that nature seems to “play the game”.
is given to us a priori, then it seems that the Born- probabilities are objectively given with it and there might be a reluctance to embrace Laplace’s principle as fundamental [9] . It seems to us that we can accept the principle as deeply rooted in our intuition and therefore to be a first principle. Authors, concerned with the many worlds interpretation in [6] [7] for instance, try to give more objective physical justifications for Laplace’s principle, mainly by describing the symmetry, which it bases on, in more physical terms. We are not sure that these ideas are really more fundamental or whether they are not the same intuition vested in different garments. We should in all this always remember that quantum states are practically given to us by making preparations, i.e. by correlating them with other systems in laboratories. It is a wonderful fact, however, that the Born-probabilities are confirmed by the corresponding frequencies, if repeated experiments are being done. This would probably not be further impressive, if quantum states would just be results of gathering measurement information. But they can also arise from an initial state by Schrödinger evolution. We at least can say that nature seems to “play the game”.
NOTES
![]()
1Under condition that the dimension of the Hilbert space is at least three.
2This follows from the fact that a general interaction evolution ![]() is unitary.
is unitary.
3Since the rational numbers ![]() are dense in
are dense in![]() , the choice of
, the choice of ![]() is general enough.
is general enough.
4This coarse-graining is used first by [6] and then by [7] in the context of many-worlds.
Let the underlying pure state ![]() have coefficients
have coefficients
![]()
5The environment could serve as a probe-system for instance.