Research on the Stability Control Strategy of Four-Wheel Independent Driving Electric Vehicle ()
1. Introduction
Four-wheel independent driving electric vehicle removes parts such as engines, clutches, gearboxes. Its structure is simpler than traditional vehicle. Because each wheel has a hub motor, it is more precise and convenient to control the torque on each wheel [1] [2] [3] . With the development of technology, consumers’ expectations for vehicle safety are also increasing. Controlling the torque on each wheel to improve the stability of the vehicle has become increasingly valuable [4] [5] [6] .
In the stability of 4WID electric vehicle research, there are four-wheel steering system and direct yaw moment control method to improve vehicle stability. However, the four-wheel steering system cannot meet the stability requirements under extreme driving condition, and the direct yaw moment control also has the accuracy problem [7] . Therefore, many researchers have focused on the use of optimized torque distribution to improve the stability of the vehicle. Yu et al. simulated the longitudinal force control assignment of the wheel drive electric vehicle, and show the effectiveness of the distribution control algorithm [8] . Ding et al. used the simple average distribution method that is one side increases the torque and the other side reduces the torque by the same amount. The control method does not take into account the vehicle’s constraint condition and the different states, and cannot accurately control the vehicle [9] . Miao used the weighted least squares method to calculate the torque distribution [10] . The weighted least squares method has the advantages in calculating the speed and iterative accuracy, but there is no solution to the case where the yaw moment is large. This paper proposes a torque distribution strategy based on longitudinal force optimization, combined with the designed layered controller and tire constraints. This strategy optimizes the torque distribution and combines with the advantages of 4WID electric vehicle chassis to achieve the stability of the vehicle control. This paper simulates 4WID electric vehicle on a double lane change and slalom. The simulation results show that the proposed control strategy can improve vehicle stability.
2. Control Strategy
2.1. Torque Distribution Control
When the vehicle is running at high speed and suddenly turns, it will cause the yaw rate to be too large and cause the vehicle to be unstable. Comparing the accelerator pedal signal and the steering wheel signal actually entered with the ideal linear two-degree-of-freedom model, the strategy calculates the additional yaw moment required and allocated torque rationally to the hub motor and the brakes on the wheels to correct the excessive yaw moment.
According to [11] , it can be seen that increasing the torque of the inner wheels of the 4WID electric vehicle and reducing the torque of the outer wheels can reduce the yaw moment of the vehicle. According to the Tang [12] , in the traditional vehicle, the front wheel brake to correct the excessive yaw moment is most effective.
This paper combines the above two methods to design a control strategy. The strategy is divided into two stages. The first stage is reducing the torque on the motor on the outer wheel when the vehicle’s yaw rate is too large and unstable. The second stage is braking the vehicle outside wheels when the torque on the outer wheels cannot guarantee the stability of the vehicle after the reduction of torque (The flow chart of control strategy is shown in Figure 1).
2.2. Torque Distribution Control Structure
The structure designed is showed in Figure 2, including drive torque controller,
![]()
Figure 1. Flow chart of control strategy.
![]()
Figure 2. Torque distribution control structure.
actuator and vehicle model. The drive torque controller is divided into an upper controller and a lower controller. The upper controller includes a speed controller, a yaw velocity controller, and a sideslip angle controller. The lower controller is the torque distributor. The upper controller calculates the desired additional yaw moment according to the state of the vehicle input and passes the torque to the lower controller. The lower controller reasonably assigns the additional yaw moment transmitted by the upper controller to the actuator according to the constraints. In Figure 2, 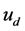 and
and 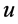 represent the target speed and actual speed of the vehicle respectively;
represent the target speed and actual speed of the vehicle respectively; 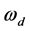 and
and 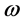 represent the ideal yaw rate and actual yaw rate of the vehicle respectively;
represent the ideal yaw rate and actual yaw rate of the vehicle respectively; 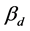 and
and 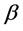 represent the ideal sideslip angle and the actual sideslip angle.
represent the ideal sideslip angle and the actual sideslip angle.
3. Controller
3.1. Speed Controller
According to the speed controller provided in [13] , the total torque 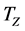 required for the vehicle is related to the front wheel angle
required for the vehicle is related to the front wheel angle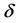 , which can be express as:
, which can be express as:
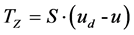 (1)
(1)
where  is proportional coefficient.
is proportional coefficient.
Since , the total torque is coordinated to the motor on each wheel. Since
, the total torque is coordinated to the motor on each wheel. Since , each wheel shares the motor torque of
, each wheel shares the motor torque of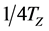 . Although the steering wheel has a large input in a short time and the speed of the vehicle is very high, but the front wheel angle is very small, this time can be considered the average torque distribution. In addition, because it is uniform speed, the difference between
. Although the steering wheel has a large input in a short time and the speed of the vehicle is very high, but the front wheel angle is very small, this time can be considered the average torque distribution. In addition, because it is uniform speed, the difference between 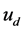 and
and 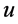 is very small, then
is very small, then 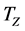 is also very small.
is also very small.
3.2. Yaw Moment Controller
The linear two-degree-of-freedom model in [14] is showed in Figure 3. The equation of motion can be expressed as:
![]() (2)
(2)
where ![]() and
and ![]() are the lateral stiffness of the front and rear wheels;
are the lateral stiffness of the front and rear wheels; ![]() and
and ![]() are the distances from the vehicle center of mass to the front and rear axle wheelbase; m is the vehicle mass;
are the distances from the vehicle center of mass to the front and rear axle wheelbase; m is the vehicle mass; ![]() is the moment of inertia of the vehicle around the Z axis. The equation of motion is rewritten in the state equation form:
is the moment of inertia of the vehicle around the Z axis. The equation of motion is rewritten in the state equation form:
![]() (3)
(3)
The approximate ideal yaw rate can be expressed by Equation (4):
![]() (4)
(4)
where ![]() is approximate ideal yaw rate;
is approximate ideal yaw rate; ![]() is wheelbase;
is wheelbase; ![]() is stability coef-
is stability coef-
ficient,![]() .
.
However, under the ground attachment limit, the lateral acceleration ![]() of the vehicle is affected by the formula (5):
of the vehicle is affected by the formula (5):
![]() (5)
(5)
where ![]() is adhesion coefficient;
is adhesion coefficient; ![]() is gravitational acceleration.
is gravitational acceleration.
When the sideslip angle is small, ignore the influence of the side angle, ![]() can be expressed by (6):
can be expressed by (6):
![]() (6)
(6)
Combining Equations (5) and (6), it can be corrected to the ideal yaw rate![]() :
:
![]() (7)
(7)
The yaw moment controller uses the PID control method to track the yaw rate and find the additional yaw moment required to maintain the vehicle’s handling stability. The difference between the actual yaw rate ![]() and the ideal yaw rate
and the ideal yaw rate ![]() is defined as
is defined as![]() :
:
![]() (8)
(8)
According to the PID control of the mathematical model can be obtained additional yaw moment![]() :
:
![]() (9)
(9)
where ![]() is the scale factor;
is the scale factor; ![]() is the integral time constant;
is the integral time constant; ![]() is the differential time constant.
is the differential time constant.
3.3. Torque Distributor
The role of the torque distributor is reasonably generalized force assigned to an actuator. For 4IWD electric vehicles, the force of each actuator refers to the wheel motor/brake applied to the tire on the longitudinal force.
1) First stage: torque distribution
Taking the left-turn condition as an example, the actual yaw moment ![]() of the vehicle and the additional yaw moment required
of the vehicle and the additional yaw moment required ![]() for the first stage can be expressed as:
for the first stage can be expressed as:
![]() (10)
(10)
![]() (11)
(11)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are longitudinal force for the left front wheel, right front wheel, left rear wheel, right rear wheel.
are longitudinal force for the left front wheel, right front wheel, left rear wheel, right rear wheel. ![]() is the distance between the wheels.
is the distance between the wheels.
As the vehicle in the uniform phase, the torque on each wheel is the same, then![]() . This stage does not control the inner wheels, and ultimately the longitudinal force on each wheel and the required torque:
. This stage does not control the inner wheels, and ultimately the longitudinal force on each wheel and the required torque:
![]() (12)
(12)
![]() (13)
(13)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are the torque for left front wheel, the right front wheel, the left rear wheel, the right rear wheel.
are the torque for left front wheel, the right front wheel, the left rear wheel, the right rear wheel.
2) Torque distribution second stage
In the first stage, when the outside wheels torque is reduced to 0, it is possible to provide the maximum additional yaw moment for the stage![]() :
:
![]() (14)
(14)
However, due to the actual yaw rate being too large, ![]() cannot meet the stability requirements. Then the second stage increases the torque of inner wheels and brakes outside wheels. The second stage requires yaw moment
cannot meet the stability requirements. Then the second stage increases the torque of inner wheels and brakes outside wheels. The second stage requires yaw moment![]() :
:
![]() (15)
(15)
The main consideration of this stage is the torque on the inner wheel and the outer wheel braking torque distribution. The expression for the objective function is:
![]() (16)
(16)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are the vertical load on each wheel,
are the vertical load on each wheel, ![]() is weight coefficient;
is weight coefficient;![]() ,
,![]() .
.
In the process of optimizing the distribution, the longitudinal force and yaw moment required for the vehicle are as follows:
![]() (17)
(17)
where![]() ,
, ![]() are brake forces on right front wheel and right rear wheel;
are brake forces on right front wheel and right rear wheel; ![]() is the force along the X axis.
is the force along the X axis.
The limits of the motor torque and ground adhesion to the wheels are as follows:
![]() (18)
(18)
![]() (19)
(19)
where ![]() is motor peak torque;
is motor peak torque; ![]() is Rolling radius.
is Rolling radius.
Substituting Equation (17) into the optimal objective function formula (16):
![]() (20)
(20)
The new objective function (20) is used to derive the ![]() and
and![]() :
:
![]() (21)
(21)
![]() (22)
(22)
Under the constraints of (21) and (22), the final solution is:
![]() (23)
(23)
![]() (24)
(24)
According to Equations (17), (23), and (24), the torque of the second stage can be calculated as:
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
4. Simulation and Analysis
This paper used Carsim and MATLAB/SIMULINK platform to build a vehicle dynamics model, a double lane change model, and a slalom model. The simulation includes double lane change maneuver and Slalom maneuver. The parameters of the simulation vehicle are shown in the following Table 1.
4.1. Double Lane Change Maneuver
To simulate the extreme driving conditions, we take the road friction coefficient of 0.2, equivalent to compaction of the snow road. The simulation is based on the comparison between without control and torque control. The simulation results are shown in Figures 4-8.
4.2. Slalom Maneuver
Simulation vehicle in situ start, accelerated to 80 km/h and road friction coefficient is 0.8. The simulation results are shown in Figures 9-13.
Figure 5 and Figure 10 show the speed curve, in the absence of control, the
![]()
Table 1. Geometric parameters of simulation vehicle.
![]()
Figure 6. Curves of lateral acceleration.
speed curve changes greatly from the original straight line instability for the lateral sliding. With torque control, the speed fluctuates slightly, but only fluctuates in a very small range. From Figure 6 and Figure 11, the lateral acceleration
curve shows that the vehicle has slipped and lost the ability to return to the normal route. With control, the situation is noticeably improved and can be returned to the normal route and the lateral acceleration which is maintained near 0 (m/s2). Figure 7 and Figure 12 show that if vehicle is out of control, the yaw rate increased rapidly with instability. In the case of control, the yaw rate is fluctuating within the range of 10 (deg/s) and tends to zero after the end of the lane to keep the vehicle stable. Figure 8 and Figure 13 show that the torque distribution control can effectively control the size of the sideslip angle, so that it is always in the vicinity of 0 (˚).
5. Conclusions
This paper has presented a control strategy to improve stability applied to a 2-DOF vehicle model. The first conclusion is that lateral acceleration, yaw rate and sideslip angle are important parameters of vehicle stability. If the value of these parameters is too large, the vehicle will be unstable.
The second conclusion is that the presented control strategy can make lateral acceleration, yaw rate and sideslip angle within a reasonable range by controlling the torque of each wheel to improve stability.
Acknowledgements
The authors are grateful to Professor Zhang Huanhuan of this research. She gives me many advices about theoretical knowledge and simulation.