Origin of Magnetic Fields of Stellar Objects in the Universe Based on the 5D Projection Theory ()
1. Introduction-Understanding Our Universe by Expanding the 4D Lorentz Manifold to the 5D Homogeneous Manifold and Project Back to the 4D Space-Time Structure via Two Projection Procedures
It is a very important step in physics to unify gravity with electrodynamics. Despite many trials, the past endeavors were unsuccessful. It is not correct to think that by adding another dimension to the Lorentz space-time, one can readily bridge gravity and electrodynamics. A unified theory along this line of thought therefore is not one that can be applied separately to a domain with masses in motion, and to another domain pertaining to dynamics of massless photons. The unified theory has to embrace both gravity and electrodynamics in an “inherent” manner. The general method we use is to analyze the physical properties of the universe via projection/mapping between the 4D and 5D space-time, with an analysis of the boundary conditions between the two domains.
In our model, after the absolute time , the universe is to be observed/ perceived. Since observation/measurement is realized after this absolute time instant, based on the uncertainty principle, the uncertainty of energy observed at
, the universe is to be observed/ perceived. Since observation/measurement is realized after this absolute time instant, based on the uncertainty principle, the uncertainty of energy observed at
this time is specified by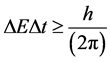 . Thus there is an infinite amount of
. Thus there is an infinite amount of
energy generated at this instant in the 5D manifold. The 5D manifold has to be homogeneous the reasons of which have been discussed in [1] . There is another reason: no physical laws have yet to be enforced. Some laws appear when the energy is perceived to be associated with e-trinos (conservation of spin, etc.).Other laws are realized when matter is being generated in the 4D Lorentz manifold. This time instant may be considered to be corresponding to the time when a Big Bang occurs in a Big Bang model discussed in literature. The term “Big Bang” in this paper therefore refers to the definition above according to the 5D theory. Starting with the above defined Big Bang concept, energy is flowing “out” along the radial direction in 4D space, and due to the Maxwell 4D boundary imposed, and any radial vector direction can become the Ricci Flow axis and generate beyond a finite 5D void core with a 4D Lorentz doughnut manifold. Since the choice of the Ricci Flow axis is arbitrary, hence many such doughnut Lorentz manifolds can be simultaneously created, thus completing the Big Bang picture of universe creation in the context of the 5D projection theory.
We assume the universe began with a homogeneous 5D space-time structure described by the above metric equation. From the homogeneous 5D manifold, we can apply projection operations [1] back onto the 4D Lorentz manifold, and requiring all the basic laws of physics to satisfy the known gauge invariance properties, so that there is consistency of mathematical logic steps linking variables in the 5D and 4D domains. We can then analyze and interpret the mathematically -deduced consequence and compare some aspects when appropriate measurable data are available.
The above projection reduction approach was presented in [1] , leading to the topological reduction of the homogenous 5D into the group representation of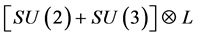 , where the L group represents the Lorentz 4D domain. It was emphasized that the resulting Poincare sphere, a “product” in projection, encloses an inhomogeneous 5D void in the center. Based on parity analysis, it has been remarked that massless spinors with equal amount of opposite charges must be present in such a void. In addition, vector potential, which gives rise to photons, must also exist inside the 5D void.
, where the L group represents the Lorentz 4D domain. It was emphasized that the resulting Poincare sphere, a “product” in projection, encloses an inhomogeneous 5D void in the center. Based on parity analysis, it has been remarked that massless spinors with equal amount of opposite charges must be present in such a void. In addition, vector potential, which gives rise to photons, must also exist inside the 5D void.
On the other hand, via the rigorous Perelman-Ricci Flow mapping [10] [11] , a homogeneous 5D is mapped into an inhomogeneous 4D doughnut structure. The consequence carries the important implication that there is a Beginning of space-time from absolute Nothing, and time is unidirectional, i.e. irreversible and the law of causality follows. This mapping procedure is then followed by Perelman’s entropy mapping [12] , via which the doughnut structure becomes a matter sphere satisfying the Lorentz manifold, thus proving Poincare’s conjecture [13] .
It is our intention to show the mathematical connections between these two mapping/projection procedures, as well as to investigate the physical outcome from such investigation in this paper, with special focus on the origin of magnetic field in the universe. Note that whatever method we employ to analyze the space-time structure of the universe, we always come up with a boundary separating the 5D and 4D domains. We start with the Fermat’s Last Theorem to analyze the space structure in the void and 4D-5D boundary in Section (2).In particular, we show that that breaking of the homogeneity of the 5D space-time, due to the imposition of the lower dimension 4D boundary, would lead to a time-frozen, 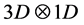 space domain, with concurrent matter formation surrounding the void. The 1D space structure is interpreted, due to parity, as an entangled state of two loops at the void-4D boundary. The generation of matter is restricted by charge parity. When the lightest lepton is generated, there must be equal amount of positive charge generated also. The generation of neutron does not violate such parity. Modification of the size of the current loop when neutrons are generated is analyzed in Section (2.3), putting forth the notion that generation of heavy elements can achieved in a similar way.
space domain, with concurrent matter formation surrounding the void. The 1D space structure is interpreted, due to parity, as an entangled state of two loops at the void-4D boundary. The generation of matter is restricted by charge parity. When the lightest lepton is generated, there must be equal amount of positive charge generated also. The generation of neutron does not violate such parity. Modification of the size of the current loop when neutrons are generated is analyzed in Section (2.3), putting forth the notion that generation of heavy elements can achieved in a similar way.
We pay special attention to the meaning and mathematical representation of homogeneity. Since other theories relating to transformation between a 5D domain and 4D domain have been published, we give a very shot review on the Kaluza-Klein (K.K.) [4] theory in Section (3). Also, we shall pay a revisit to the issue of gravitational singularity there. Note that Einstein’s unified theory [3] also followed the consequence of the K.K theory. One crucial difference between the K.K. theory, hence Einstein’s, and the present one here is that the 5D manifold of these theories are not homogenous, and the 4th space coordinate in the 5D domain is compacted to reduce dimension. We need to review this issue also because the 4th space variable in our theory is rotated to the radial direction during dimension reduction, together with the emergence of a current loop, (as a consequence of the space-space transformation) in the 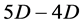 boundary where Maxwell equations must satisfy. It is precisely the existence of this non- zero space variable, as a result of the Perelman entropy mapping (leading to a
boundary where Maxwell equations must satisfy. It is precisely the existence of this non- zero space variable, as a result of the Perelman entropy mapping (leading to a  space structure) that provides the current loops that generate the intrinsic dipolar magnetic field in spherical stellar objects of the universe. Our analysis of the
space structure) that provides the current loops that generate the intrinsic dipolar magnetic field in spherical stellar objects of the universe. Our analysis of the  transformation leads us to conclude that there is no gravitational singularity in the universe.
transformation leads us to conclude that there is no gravitational singularity in the universe.
Explicit expression for the dipolar magnetic field of a general stellar object is derived in Section (4). Though the classical Biot-Savart law is employed, the quantum signature of the charge current is incorporated. The Three Laws of Dipolar Magnetic Fields of stellar objects, similar to the three laws of Stellar Angular Momentum discovered in [2] are also presented with numerical illustration in the same section there. Moreover, we have derived the ratio of the dipolar magnetic field strengths when the matter shell is composed of either (i) pure hydrogen ions, or (ii) purely Helium ions as two examples based on quark mass analysis during the generation of matter based on the dimension projection theory. As the mass density within the shell increases, the 3D space homogeneity of a shell near the surface is broken into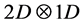 . The variation of gravity is approximately only along a direction perpendicular to the local plane on the surface. It is this broken space that leads to the atomic binding from Bohr to Chern-Simons hydrogen solution. In the relativistic limit, the Chern-Simons solution is given by the Semion state in which the electron collapses into the proton environment, bringing with it the pinned magnetic flux. We explain in Section (5) how the consequence, qualitatively, of the formation of such Semion state could lead to the generation of huge sporadic magnetic field from the stellar surface when the 2D state changes back to the 3D state, as part of the stellar evolution process. To test the general validity of the dipolar field equation we have derived, we introduce in Section (6) a new method of graphical analysis using measured values of the basic set of data (mass, radius, rotation period), and compare the power indices of the relevant variables. Very satisfactory results has been obtained for 8 different star groups: (6.1) the pre-main-sequence stars in the Orion Nebula; (6.2) the NGC 6819 stars; (6.3) the mid-to-low mass stars of the main sequence; (6.4) the pre-dwarf M34 stars; (6.5) the NGC 2516 stars; (6.6) brown dwarfs; (6.7) white dwarfs and (6.8) magnetic white dwarfs. There are two features in astronomy related to stellar magnetic field which are like mysteries. One is the linear relation between surface magnetic field
. The variation of gravity is approximately only along a direction perpendicular to the local plane on the surface. It is this broken space that leads to the atomic binding from Bohr to Chern-Simons hydrogen solution. In the relativistic limit, the Chern-Simons solution is given by the Semion state in which the electron collapses into the proton environment, bringing with it the pinned magnetic flux. We explain in Section (5) how the consequence, qualitatively, of the formation of such Semion state could lead to the generation of huge sporadic magnetic field from the stellar surface when the 2D state changes back to the 3D state, as part of the stellar evolution process. To test the general validity of the dipolar field equation we have derived, we introduce in Section (6) a new method of graphical analysis using measured values of the basic set of data (mass, radius, rotation period), and compare the power indices of the relevant variables. Very satisfactory results has been obtained for 8 different star groups: (6.1) the pre-main-sequence stars in the Orion Nebula; (6.2) the NGC 6819 stars; (6.3) the mid-to-low mass stars of the main sequence; (6.4) the pre-dwarf M34 stars; (6.5) the NGC 2516 stars; (6.6) brown dwarfs; (6.7) white dwarfs and (6.8) magnetic white dwarfs. There are two features in astronomy related to stellar magnetic field which are like mysteries. One is the linear relation between surface magnetic field 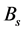 and equatorial rotation speed v in the log-log graph, and the other is the so-called “Magnetic Bode’s Law” which simply states that the parameter BsR3 and Iω relation is also linear in a log-log plot, particular for cool stars; here
and equatorial rotation speed v in the log-log graph, and the other is the so-called “Magnetic Bode’s Law” which simply states that the parameter BsR3 and Iω relation is also linear in a log-log plot, particular for cool stars; here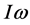 is the angular momentum. Though we have carried out a very detailed analysis of the B-v relation in Section (6) for many star groups, no suitable complete measured data sets
is the angular momentum. Though we have carried out a very detailed analysis of the B-v relation in Section (6) for many star groups, no suitable complete measured data sets 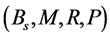 have been obtained for every star in these star groups in Section (6). Such a set of four variables for each individual star in the sun-like group with over 100 members have been published. We apply that in Section (7) to analyze the stated two mysteries. The study there is important because on face value, no parameters related to electric current are involved in the stated two relations. Where are the Maxwell equations “hidden” behind such Laws? Whereas other scientists have attempted to explain these features using various forms of dynamo theories, we find that our derived expression for the dipolar field can automatically explain such phenomena, implying that based on the 5D-4D projection theory, the co-existence of in-phase and anti-phase spinor pairs circulating in the stellar void can automatically explain the origin of angular momentum and the origin of dipolar magnetic field in stellar objects at the same time. Section (7.5) is devoted to compare the difference of the theoretical prediction and measured values of the dipole fields of some members of our planets. Section (7.6) is a summary of the laws and issues discovered in this paper. Section (7.7) concludes our endeavor. The numerical values of the relevant variables/parameters to be applied in our numerical study in this paper are all based on the fundamental well-established constants, such as electron mass, quark mass, electronic charge, the Planck constant, plus data measured only―there is no other input parameter and no parameterization process involved.
have been obtained for every star in these star groups in Section (6). Such a set of four variables for each individual star in the sun-like group with over 100 members have been published. We apply that in Section (7) to analyze the stated two mysteries. The study there is important because on face value, no parameters related to electric current are involved in the stated two relations. Where are the Maxwell equations “hidden” behind such Laws? Whereas other scientists have attempted to explain these features using various forms of dynamo theories, we find that our derived expression for the dipolar field can automatically explain such phenomena, implying that based on the 5D-4D projection theory, the co-existence of in-phase and anti-phase spinor pairs circulating in the stellar void can automatically explain the origin of angular momentum and the origin of dipolar magnetic field in stellar objects at the same time. Section (7.5) is devoted to compare the difference of the theoretical prediction and measured values of the dipole fields of some members of our planets. Section (7.6) is a summary of the laws and issues discovered in this paper. Section (7.7) concludes our endeavor. The numerical values of the relevant variables/parameters to be applied in our numerical study in this paper are all based on the fundamental well-established constants, such as electron mass, quark mass, electronic charge, the Planck constant, plus data measured only―there is no other input parameter and no parameterization process involved.
2. The Meaning of Spatial Homogeneity & Application of the Fermat’s Last Theorem to the Boundary of the 5D-4D Domains
2.1. Basics of the Special Properties of the 5D, 4D Domains and the 5D-4D Boundary
As we proceed through the paper, the physical properties of the 5D-4D boundary are of crucial importance; we therefore need to high-light some basics, which are consequence of the projection theory and fundamental physics.
a) From the 5D homogeneous metric, one can obtain a 5D second order energy-momentum differential operator without a term pertaining to mass. Solutions of such metric equation represent 5 vector potential fields (including charge-source terms, thus existence of e-trinos) traveling with speed c, similar to the fields associated with the Maxwell potentials in the 4D Lorentz manifold. In the 5D domain, a term pertaining to magnetic monopole exists. In 4D domain, the electric, magnetic symmetry is broken, so that there is no magnetic-mono- pole term in Maxwell equations.
b) In a 5D domain, a Dirac linearization process does not lead to mass creation via projection/mapping, implying the e-trinos must be massless, but charged. These spinor states are equivalent to magnetic monopole states in 5D. In 4D domain, a Dirac linearization process leads to solutions representing the state of massless, charge-neutral neutrino and the state of massive charged lepton (described by the SU(2) group) in pair form.
c) Based on (a) & (b), the states of e-trinos and 4D Maxwell potentials must form the boundary between the 5D & 4D homogeneous manifolds, implying that both classical and quantum representations are allowed in the boundary. A satisfactory quantum theory should also have such representations.
d) The void space is expressed as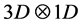 , with time frozen, meaning that the pair spinor states in 3D are orthogonal to those in 1D structure. When a pair is charge neutral, it must be in 3D space, as the product
, with time frozen, meaning that the pair spinor states in 3D are orthogonal to those in 1D structure. When a pair is charge neutral, it must be in 3D space, as the product 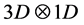 gives the Maxwell potential after a Dirac linearization process; hence such spinor pairs generate a net angular momentum
gives the Maxwell potential after a Dirac linearization process; hence such spinor pairs generate a net angular momentum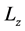 . The remaining 1D space, being orthogonal to the 3D space, then must contain no net momentum. However, similar to the appearance of the monopole term in 5D Maxwell equations, the 1D space carries a current of magnitude 2ec, which results from
. The remaining 1D space, being orthogonal to the 3D space, then must contain no net momentum. However, similar to the appearance of the monopole term in 5D Maxwell equations, the 1D space carries a current of magnitude 2ec, which results from . If such a current forms a ring or loop, with a single frequency
. If such a current forms a ring or loop, with a single frequency , then these charges will produce a magnetic dipole field, but could annihilate, and cannot remain in a perpetual state. Because the 3D space is symmetric, such a current pair loop must be split into 2 parity states in two different magnetic latitudes, one in each hemisphere. Since the 2 parity loops produces the same in line magnetic field, they will give a pure dipolar field similar to a bar magnet. The general charge neutrality within the 1D domain implies that it is possible to break the neutral charge condition between hemispheres, as long as their sum neutrality is maintained. A more detail discussion later in relation to the conformal projection P1 of these spinor states on the creation of quarks and thus hadrons will be given.
, then these charges will produce a magnetic dipole field, but could annihilate, and cannot remain in a perpetual state. Because the 3D space is symmetric, such a current pair loop must be split into 2 parity states in two different magnetic latitudes, one in each hemisphere. Since the 2 parity loops produces the same in line magnetic field, they will give a pure dipolar field similar to a bar magnet. The general charge neutrality within the 1D domain implies that it is possible to break the neutral charge condition between hemispheres, as long as their sum neutrality is maintained. A more detail discussion later in relation to the conformal projection P1 of these spinor states on the creation of quarks and thus hadrons will be given.
e) According to the P1 projection, the 4th space coordinate of e-trinos in the 5D manifold is conformally mapped into quarks of fractional charges. In order to produce a proton (composed of (u, u, d) quarks) and a neutron (composed of (u, d, d) quarks), as an example, we need 3 up and 3 down quarks. Since the 3 up quarks have a total charge of 2e, they are projected via the P1 process from 2 e-trino loop states of one loop. As the 3 down quarks have a total net charge of -e, they can be produced by P1 from just 1 anti-e-trino state from the other loop. To balance the + e charge resulting from the stated P1 projection, the Po projection on an in-phase pair (on the void surface) gives a lepton, such as an electron (exists in Lorentz space L), due to SU(2) symmetry and the unidirectional nature of time in the 5D metric. Effectively, we say that the consequence of Po is specified by the group product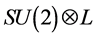 . We have overall charge neutrality in the universe all the time.
. We have overall charge neutrality in the universe all the time.
f) After the entropy mapping, or equivalently the combined Po and P1 mapping, we have a spherically shaped mass stellar object model enclosing a ![]() void filled with charged massless spinors satisfying the Fermi-Dirac distribution. We can connect the physical quantities of the thermal bath of the Fermions in the void and the physical quantities of the matter shell, leading to the discovery of the 1st and 2nd Laws regions for these spinors stated in [2] . It has been shown that under the time independent situation, eigen states of massless spinors with opposite charges, together with vector potential exist inside the void. In fact, there are eight such eigen states:
void filled with charged massless spinors satisfying the Fermi-Dirac distribution. We can connect the physical quantities of the thermal bath of the Fermions in the void and the physical quantities of the matter shell, leading to the discovery of the 1st and 2nd Laws regions for these spinors stated in [2] . It has been shown that under the time independent situation, eigen states of massless spinors with opposite charges, together with vector potential exist inside the void. In fact, there are eight such eigen states:
![]()
where p, e ,s represent the momentum, charge, and spin respectively. The in phase circulation of the oppositely charged massless spinors (with spin degeneracy![]() ) gives rise a net total angular momentum
) gives rise a net total angular momentum ![]() in the void. This angular momentum must be counter-balanced by an opposite angular momentum-
in the void. This angular momentum must be counter-balanced by an opposite angular momentum-![]() generated in the Lorentz spherical mass shell, in order to preserve total zero angular momentum value. Thus, spherical stellar objects are found to be “self-ro- tating”. In the astronomical scale for stars, this
generated in the Lorentz spherical mass shell, in order to preserve total zero angular momentum value. Thus, spherical stellar objects are found to be “self-ro- tating”. In the astronomical scale for stars, this ![]() leads to a repulsive potential within such a void, leading to the elimination of the gravitational singularity, similar to the action of the gluon repulsive potential within hadrons [14] . This aspect will be discussed in more details in Section (3).
leads to a repulsive potential within such a void, leading to the elimination of the gravitational singularity, similar to the action of the gluon repulsive potential within hadrons [14] . This aspect will be discussed in more details in Section (3).
g) In this paper, we analyze the consequence of the out of phase rotating of the spinor pairs specified by the following four state groups:
![]()
In the calculation of current, these four states lead to the spin degeneracy factor ![]() occurring in Section (4). These out of phase rotation states would generate a current of 2ec. For the 1D state to remain actually perpetual, such a 1D (pair) current state must be split into two loops, one near each magnetic pole, each carrying a current of e c (see (d) above).
occurring in Section (4). These out of phase rotation states would generate a current of 2ec. For the 1D state to remain actually perpetual, such a 1D (pair) current state must be split into two loops, one near each magnetic pole, each carrying a current of e c (see (d) above).
2.2. The Fermat’s Last Theorem and Space Time Metric
Detail of the 4D Maxwell boundary can be explicitly analyzed through Fermat's theorem, in terms of Abelian angles. The Fermat’s sum of quadratic coordinate components has been proved to be rigorous for any number of coordinate dimensions [5] .
Leonhard Euler in 1770 [15] was the first to prove that for all non-zero ![]() and
and![]() , where
, where ![]() is the set of all positive integers, the equation
is the set of all positive integers, the equation ![]() admits no solutions for n = 3. Fermat was the first to provide a proof that there is no solution for the case n = 4 (see [16] and also [17] ). It has been proved recently that
admits no solutions for n = 3. Fermat was the first to provide a proof that there is no solution for the case n = 4 (see [16] and also [17] ). It has been proved recently that ![]() has solution, a result which is referred to as the Fermat’s Last Theorem for order 2.
has solution, a result which is referred to as the Fermat’s Last Theorem for order 2.
In fact, we put forth the notion that n = 2 is the only condition that ![]() has a solution. It is not surprising, therefore, to see that in relativity, manifold representation, equations of the form
has a solution. It is not surprising, therefore, to see that in relativity, manifold representation, equations of the form ![]() repeatedly appear.
repeatedly appear.
By expanding the Lorentz manifold to the 5 space-time, we learn that the universe has a homogenous 5D space-time structure described by the metric
![]() (2.2.1)
(2.2.1)
where ![]() are the spatial vector variables; in the usual representation,
are the spatial vector variables; in the usual representation,![]() .
.
In the homogeneous 5D space-time, all 4 orthogonal space axes are exactly equivalent. Thus each axis has a measure r' as represented in the complex phase angle O(1) group [18] . This group has three elements specified by angles ![]() for the 4D orthogonal coordinates, reducing the Fermat's sum to
for the 4D orthogonal coordinates, reducing the Fermat's sum to![]() , together with the specification of angle elements in the O(1). For a 4D Maxwell space-time, this O(1) group has 2 angles:
, together with the specification of angle elements in the O(1). For a 4D Maxwell space-time, this O(1) group has 2 angles:![]() , and the transformation is specified by the Euler angles, where
, and the transformation is specified by the Euler angles, where![]() , is between 0 and
, is between 0 and![]() ;
; ![]() is between 0 and
is between 0 and![]() . It is then easy to see that for a 3D space structure, the Little group O(1) is specified by the parameter
. It is then easy to see that for a 3D space structure, the Little group O(1) is specified by the parameter![]() . For a 4D space, n has three values:
. For a 4D space, n has three values:![]() . When we fix the third angle
. When we fix the third angle ![]() to be a constant, the 5D homogeneous space-time splits into two Maxwell 4D of opposite parities. It is this explicit split that is revealed as 2 spherical gamma ray bubbles, one above and one below the Center of the Milky Way galactic core observed by NASA [19] . By this parity split, the vector potential field solutions of the 5D homogeneous metric equation with 2nd order operator breaks the 5D symmetry in the Maxwell sub-space-time, eliminating the magnetic mono-pole solution. It is also due precisely to this split, in the 5D Dirac linearized representation of the metric equation, that we have a set of e, and -e massless spinors. When these spinor fields couple to the Maxwell vector potentials, gauge transformation is satisfied. Such spinors exist only within a 5D manifold (see detailed discussion in [1] on this point). Application of projection Po on the
to be a constant, the 5D homogeneous space-time splits into two Maxwell 4D of opposite parities. It is this explicit split that is revealed as 2 spherical gamma ray bubbles, one above and one below the Center of the Milky Way galactic core observed by NASA [19] . By this parity split, the vector potential field solutions of the 5D homogeneous metric equation with 2nd order operator breaks the 5D symmetry in the Maxwell sub-space-time, eliminating the magnetic mono-pole solution. It is also due precisely to this split, in the 5D Dirac linearized representation of the metric equation, that we have a set of e, and -e massless spinors. When these spinor fields couple to the Maxwell vector potentials, gauge transformation is satisfied. Such spinors exist only within a 5D manifold (see detailed discussion in [1] on this point). Application of projection Po on the ![]() variable in the 4D Lorentz boundary creates a set of lepton masses (accompanied by neutrinos) described by the SU(2) group. We then arrive at a spinor differential operator which splits into two standard
variable in the 4D Lorentz boundary creates a set of lepton masses (accompanied by neutrinos) described by the SU(2) group. We then arrive at a spinor differential operator which splits into two standard ![]() Dirac Gamma representations. On the other hand, the 5D spinor field equation also contains a set of
Dirac Gamma representations. On the other hand, the 5D spinor field equation also contains a set of ![]() gamma matrices (Equation (7.9) of [1] ). The superposition of these 2 sets of gamma matrices in the Dirac equations in the Maxwell space-time description leads to Parity violation in weak interaction as discovered in Bethe decay. [20] .
gamma matrices (Equation (7.9) of [1] ). The superposition of these 2 sets of gamma matrices in the Dirac equations in the Maxwell space-time description leads to Parity violation in weak interaction as discovered in Bethe decay. [20] .
Since the solutions of a differential equation is totally governed by the boundary conditions that are imposed, the vector and massless charged spinor solutions to the 5D homogeneous metric operator equation are dictated by the 4D Maxwell space-time boundary which forms the enclosure to (or embracing) the 5D manifold. At the absolute time t, the space volume of the homogeneous ND manifold must have a boundary enclosure of![]() , where N is an integer. Thus the homogeneous 5D manifold boundary is the Maxwell 4D. When the Fermat's sum is expressed in term of the rotation angles and the radius magnitude, it follows that the boundary condition must reduce the 3 independent angles in 5D by fixing any one as a constant, thus reducing this set to 2 independent angles in the Maxwell 4D domain. The result is that there is imposition in alignment between
, where N is an integer. Thus the homogeneous 5D manifold boundary is the Maxwell 4D. When the Fermat's sum is expressed in term of the rotation angles and the radius magnitude, it follows that the boundary condition must reduce the 3 independent angles in 5D by fixing any one as a constant, thus reducing this set to 2 independent angles in the Maxwell 4D domain. The result is that there is imposition in alignment between ![]() of the Fermat's sum in 5D, and r that of the Fermat's sum in 4D. This boundary continuity leads to the manifestation of a Ricci Flow direction, which will convert the homogeneous Maxwell 4D boundary through the two projections (Po & P1) of the already broken symmetric property of the 4 space coordinates further into a 4D Lorentz manifold containing masses. In terms of topological mapping, this 4D Lorentz boundary manifold is precisely the doughnut structure proved by Perelman’s Ricci Flow mapping [10] [11] . In terms of the reduced 5D domain, the space structure must still have a finite region, with a center core containing the axis z(in 3D space representation) perpendicular to the doughnut plane, which is an entangled coordinate composed of the 3D coordinate z and the 4th space dimension
of the Fermat's sum in 5D, and r that of the Fermat's sum in 4D. This boundary continuity leads to the manifestation of a Ricci Flow direction, which will convert the homogeneous Maxwell 4D boundary through the two projections (Po & P1) of the already broken symmetric property of the 4 space coordinates further into a 4D Lorentz manifold containing masses. In terms of topological mapping, this 4D Lorentz boundary manifold is precisely the doughnut structure proved by Perelman’s Ricci Flow mapping [10] [11] . In terms of the reduced 5D domain, the space structure must still have a finite region, with a center core containing the axis z(in 3D space representation) perpendicular to the doughnut plane, which is an entangled coordinate composed of the 3D coordinate z and the 4th space dimension ![]() variable. The planer domain boundary in which 5D space structure still remains is then described by the Po projection of
variable. The planer domain boundary in which 5D space structure still remains is then described by the Po projection of ![]() to a 2D circle of radius
to a 2D circle of radius![]() . On the other hand, the 3D space volume of the Lorentz domain must be mapped by the remaining space variable
. On the other hand, the 3D space volume of the Lorentz domain must be mapped by the remaining space variable ![]() to 3D space via the conformal P1 (space to space) projection. This mapping in turn would give us the created leptons and the Gell-Mann quarks enclosed in this covering Lorentz boundary. It is through these projection-mapping processes imposed by the boundary condition, and the gauge invariance property, on all the massive quantum field states in the Lorentz boundary manifold, that we have created a model for the formation of a Galaxy.
to 3D space via the conformal P1 (space to space) projection. This mapping in turn would give us the created leptons and the Gell-Mann quarks enclosed in this covering Lorentz boundary. It is through these projection-mapping processes imposed by the boundary condition, and the gauge invariance property, on all the massive quantum field states in the Lorentz boundary manifold, that we have created a model for the formation of a Galaxy.
Since the determination of the Ricci Flow direction for the ![]() vector such that we obtain an entangled 3D, the z axis has infinite multiple choices from the O(1) angle between 0 and
vector such that we obtain an entangled 3D, the z axis has infinite multiple choices from the O(1) angle between 0 and![]() , it is then possible to simultaneously create many Lorentz doughnut 4D structures during the very beginning of the 5D space-time, when the absolute time is near 0, and through uncertainty, the initial energy is near infinite. In short the creation of many galaxies, near the beginning of the universe, according to the 5D projection theory, is a picture consistent with the general Big Bang theory in the literature. Furthermore, since the 5D metric of space-time implies the universe will expand continuously, in time course, expansion pushes all these created galaxies apart.
, it is then possible to simultaneously create many Lorentz doughnut 4D structures during the very beginning of the 5D space-time, when the absolute time is near 0, and through uncertainty, the initial energy is near infinite. In short the creation of many galaxies, near the beginning of the universe, according to the 5D projection theory, is a picture consistent with the general Big Bang theory in the literature. Furthermore, since the 5D metric of space-time implies the universe will expand continuously, in time course, expansion pushes all these created galaxies apart.
Our remaining problem is the general spherical shape of the massive stellar objects observed within each galaxy satisfying the Poincare Conjecture. To illustrate this topological mapping process, Perelman introduced an entropy mapping [12] , which basically closes the doughnut 5D core, into a void that contains a 3D spherical volume plus a 1D closed loop that is orthogonal to the 3D radius; this 1D loop must be on the surface of the spherical volume. Comparing projection theory and Perelman’s theory, the 3D radius of the void, is defined by the Po projection of the 4th space coordinate. This consequence is similar to that of the Ricci Flow mapping, except the matter domain totally encloses the 5D manifold. The physical state of this void is time frozen at![]() , a value specific to each stellar object. Electrons are thus created through Po outside of this void. However, overall charge neutrality must be maintained both within and outside the void in the mass shell of the stellar object. As such the measure of the 1D closed loop (hence the current density) on the spherical void surface cannot be 0, in opposition to that postulated by the KK and Einstein's theories. The measure of this 1D loop depends on the hadrons created through P1 in the Lorentz mass shell domain.
, a value specific to each stellar object. Electrons are thus created through Po outside of this void. However, overall charge neutrality must be maintained both within and outside the void in the mass shell of the stellar object. As such the measure of the 1D closed loop (hence the current density) on the spherical void surface cannot be 0, in opposition to that postulated by the KK and Einstein's theories. The measure of this 1D loop depends on the hadrons created through P1 in the Lorentz mass shell domain.
2.3. Modification of the Size of the Current Loop When Neutrons Are Generated
We note again that in the 5D manifold, there are 5 vector potential components (instead of 4 in the Maxwell domain), and 2 massless spinors with charges e and -e. [Section 2.1]. In order that these solutions satisfy the boundary conditions imposed by the Maxwell domain, we need to transform the 5 component symmetric vector potentials into the 4 Maxwell vector potentials by breaking the symmetry of solution as carefully illustrated by Maxwell in his thesis, with the emergence of a magnetic mono-pole potential, which corresponds to the 5th component vector potential in the 5D manifold. [21] [22] [23] .
We will find an explicit expression for![]() . Now the Poincare void is given by
. Now the Poincare void is given by![]() . According to Fermat's theorem, the 3D orthogonal representation is given by
. According to Fermat's theorem, the 3D orthogonal representation is given by![]() ; while
; while ![]() is orthogonal to the 1D which must form a closed loop on the spherical surface. The quantum representations are given by photons along
is orthogonal to the 1D which must form a closed loop on the spherical surface. The quantum representations are given by photons along![]() , thus the diameter 2r must satisfy integer multiple of the photon wave-length. The charged massless spinor pairs, is specified by the 1D space structure. As stated before, the current loop states, being perpetual, are split by parity into an upper and a lower hemisphere loops. The loops are therefore of radius <
, thus the diameter 2r must satisfy integer multiple of the photon wave-length. The charged massless spinor pairs, is specified by the 1D space structure. As stated before, the current loop states, being perpetual, are split by parity into an upper and a lower hemisphere loops. The loops are therefore of radius <![]() .There exists 2 parity representations all together. Thus according to the projection theory for the spinor states, the radius r, must be produced by Po, the time projection. Hence from the metric (2.2.1), with time frozen, we must have
.There exists 2 parity representations all together. Thus according to the projection theory for the spinor states, the radius r, must be produced by Po, the time projection. Hence from the metric (2.2.1), with time frozen, we must have
![]() (2.3.1a)
(2.3.1a)
While the current loop![]() , split by north and south is given by
, split by north and south is given by
![]() , where
, where ![]() (2.3.1b)
(2.3.1b)
Combining these two representations, & letting![]() , with
, with![]() , we arrive at
, we arrive at
![]() (2.3.1c)
(2.3.1c)
which determines the geometry of void boundary.
The rotation of ![]() to the radial direction is governed by the Projection Po, which takes time
to the radial direction is governed by the Projection Po, which takes time ![]() to complete. At time
to complete. At time![]() , the lightest lepton, with rest mass
, the lightest lepton, with rest mass![]() , begins to be generated, and the void radius attains the perpetual value
, begins to be generated, and the void radius attains the perpetual value![]() . We interpret P1 as the conformal projection where the residue of the variable
. We interpret P1 as the conformal projection where the residue of the variable![]() , i.e.
, i.e. ![]() (represented by c lτl, where τ is a three dimensional vector) is to be rotated to form the other orthogonal component (a ring with perimeter
(represented by c lτl, where τ is a three dimensional vector) is to be rotated to form the other orthogonal component (a ring with perimeter![]() in (2.3.1)), with gauge confinement imposed, so that a 5D domain can become a 4D domain, accompanying the generation of three quarks with total charge of + e to conserve the charge of the lightest lepton. Thus we can interpret lτl as the time at which these quarks are generated. Since the generation of these massive particles starts from nothing to reach a stationary state, we can apply the uncertainty principle with the energy-time conjugate pair. In other words, we can write
in (2.3.1)), with gauge confinement imposed, so that a 5D domain can become a 4D domain, accompanying the generation of three quarks with total charge of + e to conserve the charge of the lightest lepton. Thus we can interpret lτl as the time at which these quarks are generated. Since the generation of these massive particles starts from nothing to reach a stationary state, we can apply the uncertainty principle with the energy-time conjugate pair. In other words, we can write![]() , where n is a quantum number greater or equal to 1, with t representing the time of the stated generation of the masses, and E the total rest mass generated in each case. Note that the conformal projection of
, where n is a quantum number greater or equal to 1, with t representing the time of the stated generation of the masses, and E the total rest mass generated in each case. Note that the conformal projection of ![]() gives the SU(3) quarks, with proton as its lightest positive charged spinor particle, composed of a set of u, u, d quarks, due to gauge confinement. The bare total mass of these three quarks is precisely
gives the SU(3) quarks, with proton as its lightest positive charged spinor particle, composed of a set of u, u, d quarks, due to gauge confinement. The bare total mass of these three quarks is precisely![]() .
.
Therefore, ![]() and
and![]() . From the above two equations pertaining to uncertainty, we have the ratio
. From the above two equations pertaining to uncertainty, we have the ratio![]() . As
. As![]() , and
, and![]() , stated above, we arrive at
, stated above, we arrive at
![]() (2.3.2)
(2.3.2)
This is the size of the current loop if a pair of electron and proton is generated simultaneously; in other words, hydrogen atom is generated.
Note that charge, linear momentum, angular momentum, and energy must each be conserved during the generation of matter. We have only the lightest lepton and quarks generated initially, before the gluon potential is in action to produce proton and neutron. A set of (u, u, d) of quarks must be generated (to build up eventually a proton) together with the generation of an electron, according to the 5D projection theory. The gauge requirement for the solution on quark spinors is the charge to mass ratio![]() , a constant [24] , where j specifies the quark and its charge, we have
, a constant [24] , where j specifies the quark and its charge, we have![]() , leading to
, leading to
![]() (2.3.3)
(2.3.3)
where ![]() and
and ![]() are respectively the masses of the up and down quarks , and
are respectively the masses of the up and down quarks , and ![]() is the bare quark mass of 34 MeV. Now the sum of the bare quark masses building the proton (u, u, d) satisfies the Lorentz sum rule. Therefore we can write
is the bare quark mass of 34 MeV. Now the sum of the bare quark masses building the proton (u, u, d) satisfies the Lorentz sum rule. Therefore we can write
![]() (2.3.4)
(2.3.4)
Since mass is generated from nothing, the uncertainty principle requires that
![]() (2.3.5a)
(2.3.5a)
(as a minimum); where ![]() measures the time taken to generate the set (u,u,d) of quarks for proton. Likewise, another similar equation can be written for neutron which is composed of the set (udd):
measures the time taken to generate the set (u,u,d) of quarks for proton. Likewise, another similar equation can be written for neutron which is composed of the set (udd):
![]() (2.3.5b)
(2.3.5b)
where ![]() is the total bare quark mass building up a neutron.
is the total bare quark mass building up a neutron.
Using the data for![]() ,
, ![]() ,
, ![]() ,
, ![]() , Equation (2.3.5a) & Equation (2.3.5b) give,
, Equation (2.3.5a) & Equation (2.3.5b) give,
![]() (2.3.5c)
(2.3.5c)
However, there is also the factor due to the reduced-mass effect of the proton-neutron pair, and the reduced mass ![]() becomes (chapter 8, [1] ):
becomes (chapter 8, [1] ):
![]() (2.3.6a)
(2.3.6a)
![]() (2.3.6b)
(2.3.6b)
Hence, effectively, the time to generate a proton-neutron pair is longer than generating two protons by a factor of 2.225. Now many electrons and protons are generated simultaneously, while the 5D void is expanding until the mass shell is generated. Thus, the void radius ![]() would be larger if the mass shell is built of proton-neutron pairs, or alpha particles, namely, helium nuclei. The size of
would be larger if the mass shell is built of proton-neutron pairs, or alpha particles, namely, helium nuclei. The size of ![]() is reflected in the calculation of angular momentum as report in [2] , leading to a larger absolute value of loop size measured by
is reflected in the calculation of angular momentum as report in [2] , leading to a larger absolute value of loop size measured by ![]() in (2.3.2). In other words, the current element integral in calculating the current density generating the dipolar magnetic field in Equation (4.1.6) and hence (4.2.2a) should be multiplied by factor of
in (2.3.2). In other words, the current element integral in calculating the current density generating the dipolar magnetic field in Equation (4.1.6) and hence (4.2.2a) should be multiplied by factor of
![]() (2.3.7)
(2.3.7)
if the mass shell is composed of helium four. If the matter crust is composed of hydrogen and Helium 4, the factor b would be![]() . For more heavy elements, such as iron, the correction factor b will be different accordingly.
. For more heavy elements, such as iron, the correction factor b will be different accordingly.
With expressions (2.3.2) & (2.3.7), we can apply the magnitude of the current loop to calculate the magnetic field generated by such a loop. Before we do the application, we have to derive an explicit representation of the magnetic field generated such a current, one near each magnetic pole, when the particular element(s) is considered to be existing at the Lorentz space-time and void boundary. Such derivation will be carried out in Section (4). At the meantime, we need to analyze in the next Section about the origin of the “key” variable ![]() in the conformation mapping, which is also effectively involved in previous unified theories.
in the conformation mapping, which is also effectively involved in previous unified theories.
3. Proof of Non-Existence of Gravitational Singularity in the Universe
3.1. The Crucial Difference between the Kaluza-Klein 5D Theory, Einstein’s Unification Field Equation and Consequence of Perelman’s Two Mappings
The original Kaluza-Klein theory (KK theory, see e.g. review in [4] ) was an attempt to develop a field theory which could unify all the forces under one fundamental law. In the framework of the theory, distance squared between the two neighboring space points ![]() and
and![]() , the line element, in reference frame
, the line element, in reference frame![]() , is expressed as
, is expressed as
![]() (3.1.1)
(3.1.1)
where the usual summation rule is understood, and ![]() is the metric tensor. The space-time is uniform so far. Since the interval between P and Q is independent of the choice of reference frame, the line element (3.1.1) is invariant under the transformation between reference frames (such as from
is the metric tensor. The space-time is uniform so far. Since the interval between P and Q is independent of the choice of reference frame, the line element (3.1.1) is invariant under the transformation between reference frames (such as from ![]() to
to![]() ), so that
), so that
![]() (3.1.2)
(3.1.2)
Equating (3.1.1) to (3.1.2) gives
![]() (3.1.3a)
(3.1.3a)
where
![]() (3.1.3b)
(3.1.3b)
is called the vielbein. For a non-uniform gravitational field, the KK theory introduces the notion that “At every point in a reference frame with an arbitrary gravitational field it is possible to choose a locally inertial (freely falling) reference frame.” In other words, like carrying operation using the concept of calculus, the flat Minkowski metric can be transformed into a curved space-time metric. However, we would remark that in Equations (3.1.3a) & (3.1.3b), it was already assumed that a gravitational field is present due to the presence of the Riemannian tensor. This assumption implies that in the domain considered, mass exists. Thus the 4D is a Lorentz manifold, and by an extension to 5D space- time, such a 5D structure would not be a homogeneous 5D. Hence the Ricci- Flow mapping does not reduce this 5D back to 4D, except simply by closing the extra 4th space dimension into a closed loop.
Without going into further details, we would remark that both the KK theory and Einstein generalized field equations have difficulties to explain experimental data and interpret mathematical singularity: (i) In order to exclude the singularities in the equation set, both K.K. and Einstein introduced the method of compactness. Such an assumption leads to the models of black hole, and dark matter, which to us, are not necessary.; (ii) The electron charge e and mass me are included in a certain constant κ in K.K. theory which bridges the electromagnetic potentials and some metric tensor components including the 5th dimension. The values of both e & me deduced based on the KK theory (or Einstein’s field equations) were not consistent with the well-established experimental values then (see comments in [4] ); (iii) The KK theory (and Einstein unified field equations, [3] ) did not contain any of the nuclear forces; during that time there was lack of experimental data from accelerators and the corresponding concept in particle physics.
Concerning the key difference between their theories and projection theory developed in this series, we need to note that in KK theory, as well as Einstein's 5D metric, the proper time τ is not connected to the 4th space dimension variable. Therefore, the KK 5D is not homogeneous, neither is mass a result of space projection.
3.2. Absence of Gravitational Singularity
As analyzed in Section (2), the 1D space within the Poincare matter sphere is a set of two closed loops that includes the ![]() variable, one in each stellar hemisphere. This loop expression was employed by Einstein in his unified electrodynamic and gravity equation, as a compactization of the
variable, one in each stellar hemisphere. This loop expression was employed by Einstein in his unified electrodynamic and gravity equation, as a compactization of the ![]() variable. In his gravity solution, he then further assumed that the loop can be reduced to a structure with zero measure, and ignored the 5D space-time domain external to the doughnut domain by simply changing it to a simple Maxwell 4D space-time without the
variable. In his gravity solution, he then further assumed that the loop can be reduced to a structure with zero measure, and ignored the 5D space-time domain external to the doughnut domain by simply changing it to a simple Maxwell 4D space-time without the ![]() variable. This definitely is an error, which would lead to singularities for the gravity field both within the doughnut domain as well as outside it. It is such mathematical errors that led to the appearance of singularities in the unified theory, and the suggestion of the existence of black holes in the universe. When
variable. This definitely is an error, which would lead to singularities for the gravity field both within the doughnut domain as well as outside it. It is such mathematical errors that led to the appearance of singularities in the unified theory, and the suggestion of the existence of black holes in the universe. When ![]() is carefully retained in the space-time structure, black holes do not appear in the theory (see Wheeler’s early work [25] and a recent paper on the classical solutions of Maxwell equations [26] ). In fact, the mathematical/logical exclusion of the gravitation singularity based on simple classical physics can be realized by the following analysis. The important issue on the solutions of Maxwell equations in the 5D-4D boundary will be followed in the next section.
is carefully retained in the space-time structure, black holes do not appear in the theory (see Wheeler’s early work [25] and a recent paper on the classical solutions of Maxwell equations [26] ). In fact, the mathematical/logical exclusion of the gravitation singularity based on simple classical physics can be realized by the following analysis. The important issue on the solutions of Maxwell equations in the 5D-4D boundary will be followed in the next section.
Assuming a uniform mass distribution in a plane with the 2D void region bounded by![]() . Then the gravitation force f in the region
. Then the gravitation force f in the region ![]() must vanish. However, for the region
must vanish. However, for the region
![]()
where![]() , with D representing the 2D mass density. If
, with D representing the 2D mass density. If ![]() vanishes, according to Einstein, then f diverges as r goes to 0.This f divergence disappears when
vanishes, according to Einstein, then f diverges as r goes to 0.This f divergence disappears when![]() , or equivalently
, or equivalently![]() . From another angle, we would remark that energy flow must be conserved into the Maxwell 4D boundary. Therefore the r of the Maxwell 4D as related to the
. From another angle, we would remark that energy flow must be conserved into the Maxwell 4D boundary. Therefore the r of the Maxwell 4D as related to the ![]() of that from the 5D, is scaled by
of that from the 5D, is scaled by ![]() (see deduction leading to Equation (2.3.1b)). In quantum phase space representation, a spinor pair along r is an entangled state, and carries energy outward. It is precisely this physics that makes the doughnut core center of a galaxy, which remains in 5D, is not a black hole, since energy is radiating outward, not flowing into the center as suggested by some [27] . This is an absolutely clear reason against Einstein’s compacting
(see deduction leading to Equation (2.3.1b)). In quantum phase space representation, a spinor pair along r is an entangled state, and carries energy outward. It is precisely this physics that makes the doughnut core center of a galaxy, which remains in 5D, is not a black hole, since energy is radiating outward, not flowing into the center as suggested by some [27] . This is an absolutely clear reason against Einstein’s compacting![]() .. If we follow the analysis of the metric equation pertaining to the 5D manifold and the 5D-4D boundary as above, the 4D Maxwell space-time does not allow outward flow of e, -e massless spinor pairs that carry outward energy of 2 hν. Then at the origin of the center of the universe, or the center of the galaxy, if a black hole should exist according to those theories, mathematical logic does not indicate there is any outward flow of energy and then becomes a black hole, as we transform 4D Lorentz space-time with mass into the covariant Riemannian curvature space-time to obtain the gravity equation, since energy density seeks for uniformity. On the contrary, according to the 5D projection picture, energy seeks for uniformity by flowing outward to fill the universe at all t. Hence the singularity in the gravity field solution due to mass distribution does not appear. The above statement is both mathematical precise as well as philosophical subtle. Recently, stars of huge masses have been detected by telescopes expositions. For examples, R13601 (M = 365
.. If we follow the analysis of the metric equation pertaining to the 5D manifold and the 5D-4D boundary as above, the 4D Maxwell space-time does not allow outward flow of e, -e massless spinor pairs that carry outward energy of 2 hν. Then at the origin of the center of the universe, or the center of the galaxy, if a black hole should exist according to those theories, mathematical logic does not indicate there is any outward flow of energy and then becomes a black hole, as we transform 4D Lorentz space-time with mass into the covariant Riemannian curvature space-time to obtain the gravity equation, since energy density seeks for uniformity. On the contrary, according to the 5D projection picture, energy seeks for uniformity by flowing outward to fill the universe at all t. Hence the singularity in the gravity field solution due to mass distribution does not appear. The above statement is both mathematical precise as well as philosophical subtle. Recently, stars of huge masses have been detected by telescopes expositions. For examples, R13601 (M = 365![]() ), BAT99-98 (226
), BAT99-98 (226![]() ), R136c (230
), R136c (230![]() ), R136a2 (195
), R136a2 (195![]() ), Melnick42 (189
), Melnick42 (189![]() ), WR101c (150
), WR101c (150![]() ), LBV 1806-20 (130 to 200
), LBV 1806-20 (130 to 200![]() ) plus a long list have been detected with masses > 100 solar mass (see e.g., [6] , [7] , [8] ). If gravitational singularity were to exist, they would long have become black holes already. Such undebatable experimental results give the strongest support to our proof sketched above.
) plus a long list have been detected with masses > 100 solar mass (see e.g., [6] , [7] , [8] ). If gravitational singularity were to exist, they would long have become black holes already. Such undebatable experimental results give the strongest support to our proof sketched above.
Moreover, the finding of a ![]() two photon emission, together with neutrino obtained from the p-p collision experiment [28] and associated theoretical explanation [29] indicates that the generation of the lepton is accompanied by (neutral) neutrino. More precisely, it is shown in [29] that the spinor solution contains an oscillating phase, and the
two photon emission, together with neutrino obtained from the p-p collision experiment [28] and associated theoretical explanation [29] indicates that the generation of the lepton is accompanied by (neutral) neutrino. More precisely, it is shown in [29] that the spinor solution contains an oscillating phase, and the ![]() resonance is shown to be predictable, without the necessity to introduce a Higgs vacuum. Since no anti-neutrinos have been detected so far, such negative result supports the notion that there is no anti-matter universe, and hence no black hole. Recently, a small distinctive X-ray signal (Photon~
resonance is shown to be predictable, without the necessity to introduce a Higgs vacuum. Since no anti-neutrinos have been detected so far, such negative result supports the notion that there is no anti-matter universe, and hence no black hole. Recently, a small distinctive X-ray signal (Photon~![]() ) from the Milky Way was observed by the Nasa’s chamber satellite and the result has been interpreted as indicative of the existence of dark matter [30] . According to the 5D theory, Perelman entropy mapping process on the creation of stellar objects necessarily will lead to a short period of gamma radiation (similar to gamma radiation out of a galactic center discussed in Section (2.2)) as the object becomes a Poincare sphere. That is our model of the birth of a pulsar [2] . Therefore we do not agree to the interpretation of [30] because there are many pulsars in the region of the signal source.
) from the Milky Way was observed by the Nasa’s chamber satellite and the result has been interpreted as indicative of the existence of dark matter [30] . According to the 5D theory, Perelman entropy mapping process on the creation of stellar objects necessarily will lead to a short period of gamma radiation (similar to gamma radiation out of a galactic center discussed in Section (2.2)) as the object becomes a Poincare sphere. That is our model of the birth of a pulsar [2] . Therefore we do not agree to the interpretation of [30] because there are many pulsars in the region of the signal source.
Having analyzed the concrete role played by the space variable ![]() in the conformal mapping, we can now proceed to derive the expression of the intrinsic dipolar magnetic fields appearing in stellar objects.
in the conformal mapping, we can now proceed to derive the expression of the intrinsic dipolar magnetic fields appearing in stellar objects.
4. Explicit Expression of the Intrinsic Dipole Magnetic Field Generated by Current with Quantum Signature at the 5D-4D Interphase
4.1. Quantum Current Density of the Ring Current in the Void Boundary
During the deduction of the three laws of angular momentum in [2] , we have not included those spinor pairs circulating out of phase. They do not produce a net angular momentum, but they produce a net electric current generated by the (e, p; -e, -p) massless spinor pairs within the ![]() time frozen void.
time frozen void.
As these charges build up a stationary/perpetual current state, the wave function of a spinor pair represented by the symbol ![]() can be written as a plane wave state,
can be written as a plane wave state,
![]() (4.1.1)
(4.1.1)
where ![]() is a normalization constant, the dimension of which will be analyzed later in this section. The wave function squared gives the probability density. If there are N numbers of charges e, the charge density is defined simply as
is a normalization constant, the dimension of which will be analyzed later in this section. The wave function squared gives the probability density. If there are N numbers of charges e, the charge density is defined simply as![]() . One can get the current density J (unit to be determined by
. One can get the current density J (unit to be determined by ![]() in (4.1.1)) via
in (4.1.1)) via![]() :
:
![]() (4.1.2)
(4.1.2)
Now for non-relativistic particle with mass m moving along a circular orbit so that differentiation with respect to space variable is one-dimensional, we use the symbol ![]() to represent the momentum &v is the velocity. It is elementary to show that
to represent the momentum &v is the velocity. It is elementary to show that
![]() (4.1.3)
(4.1.3)
Since the spinor e and spinor?e are two distinguishable particles, in carrying the thermal averaging process later on, we need to calculate the number N for either type of spinors. The electric current, however, is doubled, because they are circulating out of phase in the classical sense. Therefore the overall current density in one ring is finally
![]() (4.1.4a)
(4.1.4a)
We have left our sign convention in deciding the magnetic polarity, as the sign convention is very simple. We have fixed the “classical current” to be one dimensional, ![]() , which is the track length of the current; namely,
, which is the track length of the current; namely, ![]() and , where
and , where ![]() is the void radius as defined in [2] , whereas
is the void radius as defined in [2] , whereas![]() , is a proportionality constant which is determined in Section (2). There is another factor b to be multiplied to the current ring length to include the effects of presence of various elements (hydrogen, helium) at the 5D-4D boundary. This factor will be specified if we apply our theory to find the magnetic field of specific planet or star with fuel heavier than hydrogen. Therefore, before such specification,
, is a proportionality constant which is determined in Section (2). There is another factor b to be multiplied to the current ring length to include the effects of presence of various elements (hydrogen, helium) at the 5D-4D boundary. This factor will be specified if we apply our theory to find the magnetic field of specific planet or star with fuel heavier than hydrogen. Therefore, before such specification,
![]() (4.1.4b)
(4.1.4b)
Remark again that the subscript 2 signifies that the 1D space structure has an entangled structure of two loops, composed of both e & -e spinors as explained in Section (2). Note that ![]() is the probability of finding the spinor pair in a certain region of space. Within the space allowed to be traveled by the plane wave expressed in (4.1.1), the normalization of constant should take on a value such that
is the probability of finding the spinor pair in a certain region of space. Within the space allowed to be traveled by the plane wave expressed in (4.1.1), the normalization of constant should take on a value such that ![]() in this “normalized space”. If a material wire is present, the current can only circulate around this wire and
in this “normalized space”. If a material wire is present, the current can only circulate around this wire and ![]() in (4.1.1) is the one D length l as stated above. But in quantum mechanics, a classical 1D current has a spread in space variable due to the uncertainty principle so that
in (4.1.1) is the one D length l as stated above. But in quantum mechanics, a classical 1D current has a spread in space variable due to the uncertainty principle so that ![]()
![]() where d is the spatial spread. The dimension of J is then ampere per meter, which is a physically realizable and a calculable quantity.
where d is the spatial spread. The dimension of J is then ampere per meter, which is a physically realizable and a calculable quantity.
The electrodynamics of charged massless particles moving with velocity c is not at all explored much within the frame work of Maxwell equations and the frame work of quantum field theory. An insightful investigation of the exact solution of such particles in Maxwell equations has recently been published [26] . Explicit expressions for the vector potential and the electromagnetic field were derived under the following conditions of motion of the charged massless particles: (a) linear, (b) accelerated unbounded, (c) accelerated bounded. However, unless the model charge is attached to a string (as in string theory), usually there are singularities in those solutions.
First, we would emphasize that we proposed that the existence of the massless charged spinors are represented by solution(s) of the 5D metric, rather than the 4D Maxwell potentials generated from classical massless charged particle. In fact, if the spinor solution is obtained from the massless 4D Dirac equation, with the introduction of charge, such solution must be coupled to the Maxwell potentials, and the coupled equation(s) cannot satisfy the Lorentz gauge transformation without a string attachment. Yet when this hypothetical string is reduced to zero, singularities appear in the Maxwell solutions.
It might be simple to analyze the gauge invariance property for charged massless spinor in 4D by applying the projection of the metric from 4D onto 3D (as explained in [1] ). In this case the Lorentz gauge is changed to the Chern-Simons gauge [31] . To investigate whether a massless spinor moving with c can exist in the 4D metric, let us consider the hydrogen system, where the electron is assumed to be massless. This system has a Semion ground state [32] with binding energy equal to the reduced mass, which is then zero, implying such a ground state does not exist. In general, massless charged spinors cannot be bounded in 4D Maxwell space-time. The solutions found in [26] by attaching a string, is precisely found by addition of the 4th space dimension (making the system a 5D manifold), so that a finite confinement can occur in the (added) 4th space dimension. Hence if we extend the Maxwell 4D to![]() , then a confined state of such massless charged spinors within the Maxwell 4D, due to the entangled representation between the 1D string and the 4D manifold, could exist. One can proceed and follow step by step, with the same arguments in [26] but by introducing a finite string as the 5th dimension, then we expect none of the singularities would appear if only the scalar potential is involved. On the other hand, if the stated extra dimension also includes the vector potentials, then in place of the vanished Coulomb potential (a problem stated by the authors in that stated paper), a magnetic monopole potential is then created. This monopole can be removed only if we impose that such massless charged spinors can only exist in charge neutral pairs, and not in single entity. In fact, this is one reason for us to hypothesize that one system of the charge pairs is the origin of the angular momentum of the universe [2] , and another system of charged pairs is proposed in this paper to be the origin of the magnetic field in stellar, perhaps also in other objects. We would endorse particular credit to that paper for laying stone for researchers to stand on and think deeply about the inclusion of charge massless entities traveling with c in Maxwell’s equations. Under the updated research in quantum electrodynamics, we must admit that we cannot offer analytical solution to the magnetic field generated by the charged current composed by oppositely circulating spinors pairs strictly under the regime of quantum field theory. We could proceed with our analysis, however, based on the fact that the boundary condition of the 5D manifold is the 4D Lorentz space. We propose that Maxwell’s equations are satisfied at the 5D-4D interphase. We therefore propose to generalize the solution of charged current J2 in (4.1.4b) to the relativistic case by simply replacing v by c, obtaining an estimation of the current density:
, then a confined state of such massless charged spinors within the Maxwell 4D, due to the entangled representation between the 1D string and the 4D manifold, could exist. One can proceed and follow step by step, with the same arguments in [26] but by introducing a finite string as the 5th dimension, then we expect none of the singularities would appear if only the scalar potential is involved. On the other hand, if the stated extra dimension also includes the vector potentials, then in place of the vanished Coulomb potential (a problem stated by the authors in that stated paper), a magnetic monopole potential is then created. This monopole can be removed only if we impose that such massless charged spinors can only exist in charge neutral pairs, and not in single entity. In fact, this is one reason for us to hypothesize that one system of the charge pairs is the origin of the angular momentum of the universe [2] , and another system of charged pairs is proposed in this paper to be the origin of the magnetic field in stellar, perhaps also in other objects. We would endorse particular credit to that paper for laying stone for researchers to stand on and think deeply about the inclusion of charge massless entities traveling with c in Maxwell’s equations. Under the updated research in quantum electrodynamics, we must admit that we cannot offer analytical solution to the magnetic field generated by the charged current composed by oppositely circulating spinors pairs strictly under the regime of quantum field theory. We could proceed with our analysis, however, based on the fact that the boundary condition of the 5D manifold is the 4D Lorentz space. We propose that Maxwell’s equations are satisfied at the 5D-4D interphase. We therefore propose to generalize the solution of charged current J2 in (4.1.4b) to the relativistic case by simply replacing v by c, obtaining an estimation of the current density:
![]() (4.1.5)
(4.1.5)
And the current over the ring is
![]() (4.1.6)
(4.1.6)
In passing, we would note that even if there were e & -e charges circulating in opposite directions along the 1D classical current ring, the chance of annihilation is non-zero. In general, the interaction cross-section of massive particles is larger than those of massless particles, such as photons. In fact, the strength of interaction of photons with massive particles depends strongly on the masses of the interacting particles. The cross-section area of a charge-neutral neutrino is well known to be extremely small, so that equipment to detect neutrinos is set in gold mine deep down underground. It has been estimated that there is only an upper limit on the mass of neutrino![]() , but it has not been verified that
, but it has not been verified that ![]() is zero. As in our model, the spinors are massless, we assume that their interaction cross-sections are extremely small, so that the annihilation rate of the oppositely circulating charges is practically zero, or extremely small over the life time of an stellar object. Moreover, we would remark that the interaction cross-section increases as the wavelengths of the spinor pairs are large; namely, those spinors with very low energy has a larger chance of annihilation. At temperature close to 0 K, the Fermi particles are confined mainly in the energy range of 0 to
is zero. As in our model, the spinors are massless, we assume that their interaction cross-sections are extremely small, so that the annihilation rate of the oppositely circulating charges is practically zero, or extremely small over the life time of an stellar object. Moreover, we would remark that the interaction cross-section increases as the wavelengths of the spinor pairs are large; namely, those spinors with very low energy has a larger chance of annihilation. At temperature close to 0 K, the Fermi particles are confined mainly in the energy range of 0 to![]() . The result of [2] demonstrates that those spinor particles contributing to the total angular momentum have energies
. The result of [2] demonstrates that those spinor particles contributing to the total angular momentum have energies ![]() even under the Second Law condition
even under the Second Law condition![]() .
.
4.2. Simple Representation of the Magnetic Dipolar Field Generated by the Classical Ring Current Model with Quantum Signature Incorporated
A charge current generates magnetic field in space. The Biot-Savart Law expresses the magnetic field in terms of the magnitude, spatial length, direction, and the distance from a reference point (such as the center of a ring current) of a current. According to this law, the magnetic induction field generated by a charge current density J at the space point x is
![]() (4.2.1a)
(4.2.1a)
Using elementary vector analysis,
![]() (4.2.1b)
(4.2.1b)
When the distance between the coordinate origin and the point of observation is much greater the radius of the model ring current, i.e. ![]() in (4.2.1b),
in (4.2.1b),
![]() (4.2.2a)
(4.2.2a)
![]() (4.2.2b)
(4.2.2b)
Here ![]() is the current in units of Ampere, given by expression (4.1.6) above and θ is the polar angle in the usual polar coordinate system. We need to find the number of spinors in the loop, which is
is the current in units of Ampere, given by expression (4.1.6) above and θ is the polar angle in the usual polar coordinate system. We need to find the number of spinors in the loop, which is
![]() (4.2.3a)
(4.2.3a)
where ![]() is the spin degeneracy, energy
is the spin degeneracy, energy![]() , F is the Fermi-Dirac distribution, &
, F is the Fermi-Dirac distribution, &![]() . Since
. Since ![]() , and
, and
the statistically averaged energy is![]() , so that from (4.2.3a)
, so that from (4.2.3a)
![]() ;
(4.2.3b)
;
(4.2.3b)
From (4.1.6),
![]() (4.2.4)
(4.2.4)
In view of the derivation in Appendix A, we obtain
![]() (4.2.5)
(4.2.5)
Then from (4.2.2b), the magnetic filed measured at the equator of the matter star ![]() becomes
becomes
![]() (4.2.6)
(4.2.6)
This equation may be called the Law of Intrinsic Dipole Magnetic Field for Stellar Objects.
Before we proceed to obtain numerical values to illustrate the laws we discover related to the origin of the intrinsic dipolar magnetic field of stellar objects, we need to find explicit expression of![]() . The derivation of the analytical form of this integral is given in Appendix B:
. The derivation of the analytical form of this integral is given in Appendix B:
![]() (4.2.7)
(4.2.7)
Through computer program, using Simpson’s rule of integration, the integral ![]() at
at![]() . The approximate form in Equation (4.2.7) is
. The approximate form in Equation (4.2.7) is![]() . So the approximation is very good for our estimation. Multiplied the area (as calculated via Simpson’s rule) by
. So the approximation is very good for our estimation. Multiplied the area (as calculated via Simpson’s rule) by![]() , the energy squared of spinors as weighted by the Fermi distribution =
, the energy squared of spinors as weighted by the Fermi distribution = ![]() . At
. At![]() , integration using Simpson’s rule, is 18.643. Multiplied 18.643 by
, integration using Simpson’s rule, is 18.643. Multiplied 18.643 by![]() , the energy squared of spinors as weighted by the Fermi distribution =
, the energy squared of spinors as weighted by the Fermi distribution =![]() , not much different from the case with
, not much different from the case with![]() . At
. At![]() , integration via Simpson’s rule, is 0.86332. The energy of spinors as weighted by the Fermi distribution
, integration via Simpson’s rule, is 0.86332. The energy of spinors as weighted by the Fermi distribution ![]() , which is over two orders of magnitude higher than the case with
, which is over two orders of magnitude higher than the case with![]() . Since the integral is directly proportional to the magnetic field, it means that there must be a sudden change in the integral
. Since the integral is directly proportional to the magnetic field, it means that there must be a sudden change in the integral ![]() over
over![]() , similar to the Laws reported in [2] .
, similar to the Laws reported in [2] .
We now plot the I versus T graph, since ![]() Joule is a universal constant, considering it as the rest mass of the lightest lepton created. Figure 1 shows such a graph, indicating clearly that there is a rather sharp transition, in line with our numerical analysis just stated. The graph representing Equation (4.2.7) is composed of the green straight line, and the red horizontal line, plus the blue transition curve. In fact, let us consider the situation at very high temperature
Joule is a universal constant, considering it as the rest mass of the lightest lepton created. Figure 1 shows such a graph, indicating clearly that there is a rather sharp transition, in line with our numerical analysis just stated. The graph representing Equation (4.2.7) is composed of the green straight line, and the red horizontal line, plus the blue transition curve. In fact, let us consider the situation at very high temperature
Such that![]() . Take
. Take![]() ,
, ![]() , the two summations in (4.2.7) cancel, so that
, the two summations in (4.2.7) cancel, so that ![]() is approximated by
is approximated by
![]() (4.2.8a)
(4.2.8a)
For even greater temperature such as![]() ,
,
![]() (4.2.8b)
(4.2.8b)
to good approximation. The straight green line in Figure 1 with a constant positive slope represents such a line.
On the other hand, if the temperature is relatively low, such that![]() , the integral in (4.2.7) takes on a constant value of
, the integral in (4.2.7) takes on a constant value of
![]() (4.2.9)
(4.2.9)
In Figure 1, the integral in this region is represented approximately by a redhorizontal line. The intersection of the above two straight lines cross at the
![]()
Figure 1. The integrand, as depicted in expression (4.2.7), is a function of temperature T (K). The straight green line with a constant positive slope represents the approximate solution given by Equation (4.2.8b). The red horizontal line represents the approximate solution indicated by Equation (4.2.9). The two straight lines intersect at. T = 3.2 ´ 109 K. We observe that the stated approximated solutions in the “low/cold” and “high/hot” temperature ranges are very good.
temperature![]() . This is the transition temperature, which is > Bethe temperature of fusion.
. This is the transition temperature, which is > Bethe temperature of fusion.
We would emphasize that integral ![]() is not the only function that could be T-dependent in calculating magnetic field. In Equation (4.2.6),
is not the only function that could be T-dependent in calculating magnetic field. In Equation (4.2.6),
![]()
can also be separated into two regions in temperature. Under the First Law of the angular momentum, i.e.![]() ,
,
![]() (4.2.10)
(4.2.10)
In view of Equations (4.2.8b) & (4.2.10), we obtain the Law of Intrinsic Dipole Magnetic Field for Hot Stars below:
![]() (4.2.11)
(4.2.11)
As P&R are dependent implicitly on T, when T is large, P is small, and one has to carry out detailed numerical analysis before one can learn how B(eq) varies with T in realistic samples. Moreover, all the equations for B(eq) hold under the condition of![]() . In case the matter shell is thin, a more complicated procedure is needed to study the angular momentum (and hence B) as demonstrated in [2] on the analysis of Pulsar angular momentum. Due to limitation in space, we shall not study stars at very high temperature in this paper as it will be
. In case the matter shell is thin, a more complicated procedure is needed to study the angular momentum (and hence B) as demonstrated in [2] on the analysis of Pulsar angular momentum. Due to limitation in space, we shall not study stars at very high temperature in this paper as it will be
equally complicated. Here we want to emphasize that ![]()
can be separated into two regions in T. At small T and large T, the asymptotic lines are respectively two straight lines (one horizontal, and one with positive slope) intersecting at ![]() several times of
several times of![]() , as demonstrated in [2] . The above integral is in the denominator of (4.2.11). The analysis of the property of
, as demonstrated in [2] . The above integral is in the denominator of (4.2.11). The analysis of the property of ![]() above, which is in the numerator, together with the result of [2] tells us
above, which is in the numerator, together with the result of [2] tells us
right away that ![]() is a constant for a wide
is a constant for a wide
cool region. Inspection of (4.2.11) reveals that therefore B(eq) depends explicitly only on the mechanical variables in front of the quotient of the state two integrals. This is a very crucial aspect of our discovery.
Under the regime of the Second Law of angular momentum, we present in Appendix B, the approximate expression of statistically weighted over![]() :
:
![]()
and Equation (4.2.9) already gives the approximate expression for the integral![]() . The equatorial magnetic field as depicted in (4.2.6) becomes
. The equatorial magnetic field as depicted in (4.2.6) becomes
![]() (4.2.12)
(4.2.12)
where
![]() (4.2.13)
(4.2.13)
Recalling that![]() . For convenience of computation,
. For convenience of computation,
![]() (4.2.14)
(4.2.14)
We may call Equation (4.2.12) as the Law of Intrinsic Dipole Magnetic Field for Cool Stellar Objects. This equation will be used throughout the numerical analysis in this paper.
We have deduced the magnetic expression understand the Second Law condition because we are interested in finding the dipole field when the matter shell has been formed and the temperature of the void-matter boundary is not too high ![]() in this paper. The huge magnetic field generated by quark current has been treated qualitatively in [2] . The intrinsic dipole field of pulsars where T is very high, will be treated elsewhere. It is important to note that according our theory, the dipole field intensity can be calculated if we know the “mechanical variables” (M, R, P). The very large magnetic field of stars near their end stage of evolution will be discussed in a later section.
in this paper. The huge magnetic field generated by quark current has been treated qualitatively in [2] . The intrinsic dipole field of pulsars where T is very high, will be treated elsewhere. It is important to note that according our theory, the dipole field intensity can be calculated if we know the “mechanical variables” (M, R, P). The very large magnetic field of stars near their end stage of evolution will be discussed in a later section.
5. On the Plausible Origin of Huge Non-Dipolar Strong Magnetic Fields of Many Stars, Including the Old/Dying Ones
It has been shown that the Maxwell and Chern-Simon gauge theories are coupled/compatible and the charge flux pinning phenomenon can be realized by the Maxwell-Chern-Simons gauge theory in a 2D system [31] [32] [33] .
Now the confinement of a 3D hydrogen to a 2D state is supported by the fact that exact analytical solutions for 2D hydrogen can be derived for the non-relati- vistic and the relativistic H-atom model [34] [35] . From the view point of the Bohr’s model, the exact solutions for the relativistic ground state of the 2D-hy- drogen atom gives a binding energy as large as the reduced mass of the composite system [34] . The consequence is that the binding energy plus the rest energy of the system can become zero if the positive charge (the center of attraction) is much more massive than the electron. In other words, a 2D or collapsed hydrogen atom hydrogen atom can approach a Semion state, with magnetic flux attached to every electron [33] .
When a star has a large mass (such as the sun) and a small radius (such as the terrestrial radius), a large gravitation gradient exists along the radial direction, confining the motion of electrons from a 3D space to a ![]() space structure, considering the stellar surface to be a plane in a local region.
space structure, considering the stellar surface to be a plane in a local region.
From the symmetry point of view, we say that the 3D space homogeneity is broken into![]() , with gravity field along the 1D. It is this broken space homogeneity that leads to the atomic binding from Bohr to Chern-Simons hydrogen solution. In the relativistic limit, the Chern-Simons solution is given by the Semion state, where the electron collapses into the proton environment, bringing with it the pinned magnetic flux. Since the Semion state is applicable to all elements, and not just for the hydrogen, massive neutral objects including atomic structures, can be considered in such
, with gravity field along the 1D. It is this broken space homogeneity that leads to the atomic binding from Bohr to Chern-Simons hydrogen solution. In the relativistic limit, the Chern-Simons solution is given by the Semion state, where the electron collapses into the proton environment, bringing with it the pinned magnetic flux. Since the Semion state is applicable to all elements, and not just for the hydrogen, massive neutral objects including atomic structures, can be considered in such ![]() space manifold near the stellar surface. The atomic Coulomb binding between a nucleus and its outermost electron is no longer described by the homogeneous Coulomb potential alone, but must also include a difference in energy between the gravitation potential at the nucleus
space manifold near the stellar surface. The atomic Coulomb binding between a nucleus and its outermost electron is no longer described by the homogeneous Coulomb potential alone, but must also include a difference in energy between the gravitation potential at the nucleus![]() , and that of the electron
, and that of the electron![]() ; where
; where ![]() &
& ![]() are respectively the nucleus& electron masses;
are respectively the nucleus& electron masses; ![]() are the (radial) distances between the center of the star to the nucleus and electron respectively. From the 5D theory
are the (radial) distances between the center of the star to the nucleus and electron respectively. From the 5D theory ![]() are both greater than void radius
are both greater than void radius![]() . Setting
. Setting![]() ,
,
![]() (5.1)
(5.1)
via simple expansion of![]() . Now
. Now ![]() if the nucleus is proton. The ratio
if the nucleus is proton. The ratio ![]() is of different scale and must be much smaller than that. Therefore
is of different scale and must be much smaller than that. Therefore
![]() .
.
Hence for non- zero h values, the gravitational potential difference ![]() is mainly modified by the (positive)factor
is mainly modified by the (positive)factor![]() and has a bigger absolute value; this modification effect is larger for larger h(which is atomic size), so far as
and has a bigger absolute value; this modification effect is larger for larger h(which is atomic size), so far as![]() , a condition always satisfied . The physical consequence is that if the gravitation potential is mainly on the radial direction, the electrons tend to escape from the stellar surface, and away from the nucleus. Let us include the effect of the binding energy of a Semion state and Coulomb potential also. Now the exact binding energy of the Semion ground state energy is
, a condition always satisfied . The physical consequence is that if the gravitation potential is mainly on the radial direction, the electrons tend to escape from the stellar surface, and away from the nucleus. Let us include the effect of the binding energy of a Semion state and Coulomb potential also. Now the exact binding energy of the Semion ground state energy is ![]() [35] , which is equal to?(kinetic energy + Coulombic potential energy+
[35] , which is equal to?(kinetic energy + Coulombic potential energy+![]() ).Here the relativistic kinetic energy is
).Here the relativistic kinetic energy is![]() , and the Coulombic potential energy is
, and the Coulombic potential energy is![]() , where
, where ![]() is the distance between the nucleus and the associated electron. In other words,
is the distance between the nucleus and the associated electron. In other words,![]() . On the stellar surface,
. On the stellar surface, ![]() is small compared to V in magnitude. We can say that effectively the Coulomb potential under (Semionic) gauge constrain gives rise to the relativistic electron mass. Due to pressure fluctuation, and the fact that surface temperature is at least several thousand K, some of the Semions readily have enough kinetic energy to escape the Coulombic &gravitation pull, and the pinned magnetic flux is released, together with relativistic electrons.
is small compared to V in magnitude. We can say that effectively the Coulomb potential under (Semionic) gauge constrain gives rise to the relativistic electron mass. Due to pressure fluctuation, and the fact that surface temperature is at least several thousand K, some of the Semions readily have enough kinetic energy to escape the Coulombic &gravitation pull, and the pinned magnetic flux is released, together with relativistic electrons.
Let us take some concrete examples. It is well-known that magnetic storms are found to be periodic on the solar surface. We anticipate that the solar motion participates in the occurrence of periodicity. Thus if the gravitational potential difference (as a matter pressure) is the cause of Semion states formation, such states are likely to be formed slightly below the photosphere. Cyclic plasma turbulence could bring the Semion states to the surface, and the ![]() structure could change back to a 3D structure, releasing magnetic flux in a cyclic manner, as explained in [36] . The consequence is the occurrence of flares and radio wave storms (emitted by the maser effect of relativistic electrons via cyclotron radiation). In fact, close to 100% circular polarized radio waves have been reported from Brown Dwarfs and the sun [37] [38] [39] . Based on the frequency of the emission, the magnetic field at the source is calculated, as will be discussed further in Section (7).
structure could change back to a 3D structure, releasing magnetic flux in a cyclic manner, as explained in [36] . The consequence is the occurrence of flares and radio wave storms (emitted by the maser effect of relativistic electrons via cyclotron radiation). In fact, close to 100% circular polarized radio waves have been reported from Brown Dwarfs and the sun [37] [38] [39] . Based on the frequency of the emission, the magnetic field at the source is calculated, as will be discussed further in Section (7).
We would note also that the star will be positively charged and would attract negatively charged particles with low kinetic energy. Note for small stars such as Magnetic White Dwarfs![]() , when gravity is strong enough to provide the necessary condition for Semion states to exist, but at relative higher temperature, Semions can escape, releasing huge magnetic field as stated. Electrons leave the star, leading to reduction of stellar mass. As the star further collapses, its gravity becomes far too strong for Semions to escape, and the surface magnetic storms cease. Many White Dwarfs have masses between
, when gravity is strong enough to provide the necessary condition for Semion states to exist, but at relative higher temperature, Semions can escape, releasing huge magnetic field as stated. Electrons leave the star, leading to reduction of stellar mass. As the star further collapses, its gravity becomes far too strong for Semions to escape, and the surface magnetic storms cease. Many White Dwarfs have masses between![]() , showing irregular or weak magnetic field. We speculate that White Dwarfs could well be the “older stage” of Magnetic White Dwarfs which have larger masses.
, showing irregular or weak magnetic field. We speculate that White Dwarfs could well be the “older stage” of Magnetic White Dwarfs which have larger masses.
Let us “borrow” some result in condensed matter physics to estimate the magnitude of magnetic field generated by a group of Semions. The 2D number density of composite fermion system σ is related to the magnetic field B by (see e.g. [31] )
![]() (5.2)
(5.2)
where n is the “level” of quantum flux and ![]() is the unit quantum flux given by h/e. We should note that the magnetic field is pinned in the Semion layer. We propose during the evolution, a star could go through first the change in matter density leading to a situation that would favor the formation of 2D Semion state near its surface as sketched above.
is the unit quantum flux given by h/e. We should note that the magnetic field is pinned in the Semion layer. We propose during the evolution, a star could go through first the change in matter density leading to a situation that would favor the formation of 2D Semion state near its surface as sketched above.
Suppose for rough estimation, let us take a magnetic white dwarf WD0011134 associated with the set of data![]() , giving mass density of
, giving mass density of ![]() [40] . Whereas helium plus other heavier elements are formed near the matter center region, suppose there are still Semion layers whose total area amounts to the whole surface area of
[40] . Whereas helium plus other heavier elements are formed near the matter center region, suppose there are still Semion layers whose total area amounts to the whole surface area of![]() , as an upper limit estimation. Recalling the diameter of a hydrogen atom is 120 pm, mass of proton is
, as an upper limit estimation. Recalling the diameter of a hydrogen atom is 120 pm, mass of proton is![]() , the total number of hypothetical Semions there is
, the total number of hypothetical Semions there is
![]() (5.3)
(5.3)
taking the level n = 1 as the upper limit of the magnetic field B estimation. The 2D density of Semion, from Equation (5.2), is therefore
![]() (5.4)
(5.4)
If Semions in the whole surface layer have enough energy to overcome gravitational and Coulomb attractions, the average magnetic field (which is radial in directions) over the whole stellar surface, being hypothetical released is then
![]() (5.5)
(5.5)
It is known that the magnetic fields of Magnetic White Dwarfs are non-dipo- lar and distributed irregularly [40] . Thus to produce a magnetic field of ![]() in certain surface areas for the particular MWD as observed, it is necessary that only a small region of the hypothetical Semion layer with area
in certain surface areas for the particular MWD as observed, it is necessary that only a small region of the hypothetical Semion layer with area ![]() of the stellar surface forms the Semion state. When those Semions covering only
of the stellar surface forms the Semion state. When those Semions covering only ![]() of the surface area change from 2D back to 3D structure, a magnetic field ~
of the surface area change from 2D back to 3D structure, a magnetic field ~ ![]() will be released. Note that it is the flux that can be taken as the “absolute measure”, because when the magnetic flux lines are released and spread out to a certain area A, say, the magnetic field is flux/A. Without more observable information, we cannot compare the theoretical result and the detected magnitude of the sporadic magnetic field. The above rough order of magnitude estimation points to the fact that it is feasible that pressure wave oscillations in our model could explain qualitatively the huge magnetic field detected in MWD and other old stars.
will be released. Note that it is the flux that can be taken as the “absolute measure”, because when the magnetic flux lines are released and spread out to a certain area A, say, the magnetic field is flux/A. Without more observable information, we cannot compare the theoretical result and the detected magnitude of the sporadic magnetic field. The above rough order of magnitude estimation points to the fact that it is feasible that pressure wave oscillations in our model could explain qualitatively the huge magnetic field detected in MWD and other old stars.
Note that this final stage of the star still possess the ![]() void center, which might or might not have enough massless charged spinors to maintain a self-rotation or dipolar magnetic field. In fact, according to our theory, the void radius
void center, which might or might not have enough massless charged spinors to maintain a self-rotation or dipolar magnetic field. In fact, according to our theory, the void radius ![]() for cool stars. As the radius of the stars becomes smaller, even though the mass can increase, the increase in P due to loss of energy from the void as the star cools down, can cause a reduction in
for cool stars. As the radius of the stars becomes smaller, even though the mass can increase, the increase in P due to loss of energy from the void as the star cools down, can cause a reduction in![]() of stars can vary in very complicated ways as shown by many examples in Section (6) later. In the limit when Ro approaches zero, the explicit expression of B (equatorial) shows that it becomes zero, together with
of stars can vary in very complicated ways as shown by many examples in Section (6) later. In the limit when Ro approaches zero, the explicit expression of B (equatorial) shows that it becomes zero, together with ![]() too― this is how a star “dies” in our theory.
too― this is how a star “dies” in our theory.
6. Analysis of the Variation of the Theoretically Derived Dipole Magnetic Field with Respect to Change of the Basic Features of a Star
6.1. Introduction with a Set of Data of the Halo Stars in the Orion Nebula
We have derived the equatorial magnetic surface field in terms of the basic/“raw” data set (M, R, P):
![]() (6.1.1)
(6.1.1)
We define the set of variables (M, R, P) as the basics/raw data variables. In some stars, all the three variables can be measured, but the number of such stars is small, and the accuracy of measurement is left with some high degree of uncertainty. In some star groups, the radius can only be theoretically deduced; a typical example is the application of the Hamada-Salpeter equation [41] to obtain the radii of (cool) dwarf stars with values of mass as input data. The above expression is valid only when the angular momentum is equal to that of a solid sphere with the same mass density, as a zero-order approximation. In stars, the matter sphere is built of magnetized plasma while fusion processes proceed to build up heavier elements. Eventually, we have neutron stars as briefly sketched in [2] . Essentially, therefore the three basic variables are inter-connected. We will leave the more detailed discussion on the laws we discover in the next section. As the rotation periods of pulsars have been observed to be slowed down continuously, and such an aspect is intuitively true from the consideration of energy conservation, obviously the B-P relation of different star groups would bring us useful information in stellar structure and stellar evolution. Therefore, we focus on the variation of the equatorial/polar field with respect to changing period of rotation first. We remark that the normalized void radius ![]() is a function of mass density, as analyzed in our previous paper [2] . In this paper, we have found theoretically that the surface dipole field is proportional to
is a function of mass density, as analyzed in our previous paper [2] . In this paper, we have found theoretically that the surface dipole field is proportional to![]() . Therefore, we have to take data for stars within a relatively close range of density as a subgroup in our investigation. We will introduce the methodology of our analysis as we follow a number of star groups.
. Therefore, we have to take data for stars within a relatively close range of density as a subgroup in our investigation. We will introduce the methodology of our analysis as we follow a number of star groups.
So we begin with the pre-main ?sequence or hollow stars of the Orion Nebula. Data of these stars in the Milky Way are taken from [42] . Here the mass![]() , radius
, radius![]() , period of rotation P(days)are “basic data”. Only stars with density D greater than
, period of rotation P(days)are “basic data”. Only stars with density D greater than ![]() are included. This number is arbitrary, but the choice is based on the idea that we analyze objects with a rather concrete spherical-like structure. Inclusion of the lower density ones does not affect the result. The surface equatorial magnetic field B (eq, theory, Gauss) has been derived in Section (4) to be expressible as a function of the basic parameters only. Under the condition of the Second Law of angular momentum
are included. This number is arbitrary, but the choice is based on the idea that we analyze objects with a rather concrete spherical-like structure. Inclusion of the lower density ones does not affect the result. The surface equatorial magnetic field B (eq, theory, Gauss) has been derived in Section (4) to be expressible as a function of the basic parameters only. Under the condition of the Second Law of angular momentum ![]() with Fermi energy
with Fermi energy ![]() (rest mass of electron), we calculate this B, the void radius Ro, the magnetic parameter
(rest mass of electron), we calculate this B, the void radius Ro, the magnetic parameter![]() , the angular momentum
, the angular momentum![]() , density and enter these values for each star in Table 1.
, density and enter these values for each star in Table 1.
Figure 2(a) and Figure 2(b) show the B(equatorial)-P graphs for the density ranges of 48 - 100, and 100 - 160 ![]() respectively. The average den-
respectively. The average den-
![]() (a)
(a)![]() (b)
(b)
Figure 2. (a) The surface equatorial magnetic field B (eq, Gauss) vs the period of rotation P(s) for stars in the Orion of the Milky Way with mass density between about 48 to 100 kg/m3. The one off star is reported to have a radius of 3.23 solar radii, and consider that is out of the group. The correlation is over 0.9 if we take off this “off-line” sample. We keep it there to show that when the density is too low, the B-P relation is deviated from linear in the log-log plot. The maximum of horizontal axis is 106 s. See data in Table 1; (b) The surface equatorial magnetic field B(eq, Gauss) vs the period of rotation P(s) for stars in the Orion of the Milky Way with mass density between about 100 to 160 kg/m3, using data in Table 1. The correlation is good and power index is −0.69. Though the correlation is good, further analysis as shown in the text indicates that the comparison between theory and experimental data is not simple, and several steps are needed, and the methodology becomes clearer as we go through the other sub-sections following.
![]()
![]()
Table 1. Data of the pre-main-sequence stars in the Orion Nebula in the Milky Way are taken from [42] . Here the mass![]() , radius
, radius![]() , period of rotation P(days)are “basic data”. Stars with density D greater than
, period of rotation P(days)are “basic data”. Stars with density D greater than ![]() are included. This number is arbitrary, but the choice is based on the idea that we analyze objects with a rather concrete spherical-like structure. Inclusion of the lower density ones does not affect the result. The surface equatorial magnetic field B (eq, theory, Gauss) has been derived in Section (5) to be expressible as a function of the basic parameters only. Under the condition of the Second Law of angular momentum
are included. This number is arbitrary, but the choice is based on the idea that we analyze objects with a rather concrete spherical-like structure. Inclusion of the lower density ones does not affect the result. The surface equatorial magnetic field B (eq, theory, Gauss) has been derived in Section (5) to be expressible as a function of the basic parameters only. Under the condition of the Second Law of angular momentum ![]() with Fermi energy
with Fermi energy ![]() (rest mass of electron), we calculate this B, the void radius
(rest mass of electron), we calculate this B, the void radius![]() , the magnetic parameter
, the magnetic parameter![]() , the angular momentum
, the angular momentum![]() , density and enter these values for each star in the table.
, density and enter these values for each star in the table.
sity of the stars in Figure 2(a) is very low, and we neglect the mathematical analysis. The B-P plot in Figure 2(b) for stars with density in the range of about 1.0 - 1.6 ![]() gives an expression
gives an expression
![]() (6.1.2)
(6.1.2)
Substituting (6.1.2) into (6.1.1), we arrive at
![]() ,
,
Or
![]() (6.1.3)
(6.1.3)
Further analysis shows that there is no clear mathematical relation of the P-R plot, nor the P-M plot, using the raw data. In other words, we cannot compare the theoretical prediction and experimental relations for this group of stars. Such a result is to be expected, because they are halo stars and the theory assumes that the angular momentum expression to be represented by![]() . The average density of this pre-main sequence stars is one order smaller than the sun, which is a lump of plasma, and is several hundred times smaller than that of the earth. As we proceed to analyze different groups with greater density, the comparison between theory and raw data becomes valid.
. The average density of this pre-main sequence stars is one order smaller than the sun, which is a lump of plasma, and is several hundred times smaller than that of the earth. As we proceed to analyze different groups with greater density, the comparison between theory and raw data becomes valid.
6.2. NGC 6819 Stars
We proceed with another group of stars with larger density, since the magnitude of B is sensitive to density values. Parameters include mass M in units of solar mass![]() , radius R (in units of solar radius
, radius R (in units of solar radius![]() ), the period of rotation
), the period of rotation ![]() of 30 stars in NGC 6819 according to [43] . The masses are read approximately from the data points of the
of 30 stars in NGC 6819 according to [43] . The masses are read approximately from the data points of the ![]() graph of [43] . The radius is deduced according to the following equation:
graph of [43] . The radius is deduced according to the following equation:![]() , for
, for ![]() as in reference [44] . The other variables are calculated and entered into Table 2, with the same setting of Table 1.
as in reference [44] . The other variables are calculated and entered into Table 2, with the same setting of Table 1.
First, we plot the B − P graph in log scale using the measured basic variables (established expression like mass-radius relation for dwarfs). Figure 3 gives such a graph with a negative slope of −0.584. Equation (6.1.1) can then be written as
![]() (6.2.1)
(6.2.1)
Since the correlation is very good, we can assume that
![]() (6.2.2)
(6.2.2)
is valid, and Equation (6.2.1) becomes
![]() (6.2.3)
(6.2.3)
Since the stars are associated with various values of the sets (M, R, P), if Equation (6.2.2) is to be approximately true, these variables must vary in such a way that the function F1 is approximately a constant. We plot in Figure 4 the values of F1 for these 30 stars using the raw data from Table 2. There are some fluctuations, but in a rough way, we can proceed to analyze Equation (6.2.3), taking F1 as a constant.
![]()
Figure 3. The variation of the theoretical surface magnetic fields B (eq, theory, Gauss) of NGC 6819 stars with changing period of rotation P(s), according to the 5D theory. The data are taken from numbers entered into Table 2. The slope of the log-log plot is about minus 0.584.
![]()
Figure 4. Values of the function F1 for 30 stars in NGC 6819. The upper horizontal line represents the value 3.0 ´ 108. The average of these 30 numbers is about 2.5 ´ 108 (SI units).
Equation (6.2.2) can then be approximated by:
![]() (6.2.4a)
(6.2.4a)
Or
![]() (6.2.4b)
(6.2.4b)
Employing raw data from Table 2 for different star members of the NGC 6819 group, the graph of log P against log R is linear with a slope of -3.76 (see Figure 5), so that Equation (6.2.4b) can be expressed as
![]() (6.2.5)
(6.2.5)
Or
![]() (6.2.6)
(6.2.6)
Or
![]() (6.2.7)
(6.2.7)
Note that the above equation is the consequence of the theoretically derived Equation (6.2.1), with the use of the P-R relation from measured data. To test the validity of the theory, we now use the raw data sets (M, R) from Table 2, and plot their relation in Figure 6 below. This graph gives a power index of 1.0612. Observing that there are variations of data of this group of stars with density several hundred of![]() , the comparison can be considered to give satisfactory result. Recollecting no such comparison is possible for pre-main sequence stars with mass density up to 160
, the comparison can be considered to give satisfactory result. Recollecting no such comparison is possible for pre-main sequence stars with mass density up to 160![]() , we observe that we might arrive at better results with other star groups with larger mass density (and/or more accurate data) in later sub-sections.
, we observe that we might arrive at better results with other star groups with larger mass density (and/or more accurate data) in later sub-sections.
Following, Figure 7 shows the variation of the theoretical surface magnetic fields B (eq, theory, G) of NGC 6819 stars with changing values of the void radius![]() . The result indicates that for larger void size, the surface magnetic field is larger because the effective number of spinor pairs rotating in opposite direction is also larger. The variation of
. The result indicates that for larger void size, the surface magnetic field is larger because the effective number of spinor pairs rotating in opposite direction is also larger. The variation of ![]() vs density
vs density ![]() is shown in Figure 8, giving slope of −0.867. Such a result suggests that those
is shown in Figure 8, giving slope of −0.867. Such a result suggests that those
![]()
Figure 5. Employing raw data values in Table 2, this graph shows the variation of the period P with different values of the radius R for different star members. The slope of the above graph is −3.761. The maximum of horizontal axis is 2 ´ 109 m.
![]()
Figure 6. The Mass?radius relation using raw data from Table 2. The slope of the power relation is 1.0612. As a very rough estimation, we predict from theory that the slope of the log M-log R plot is 1.168. The maximum value on the horizontal axis is 2.0 ´ 109 m.
![]()
Figure 7. The variation of the theoretical surface magnetic fields B (eq, Gauss) of NGC 6819 stars with changing void radius ![]() indicates that for larger void size, the surface magnetic field is larger because the effective number of spinor pairs rotating in opposite direction is also larger. For other basic parameters and calculated variables, refer to Table 2. The slope of this log-log plot is about 1.3. The maximum of the horizontal axis is 2.0 ´ 106 m.
indicates that for larger void size, the surface magnetic field is larger because the effective number of spinor pairs rotating in opposite direction is also larger. For other basic parameters and calculated variables, refer to Table 2. The slope of this log-log plot is about 1.3. The maximum of the horizontal axis is 2.0 ´ 106 m.
stars have larger void radius Ro when the mass density is low, suggesting that gravity contraction causes the void size to decrease, but at a very slow rate because the value of the slope is not far from unity. We would investigate whether such effect is similar to other star groups, and the power index should in principle, indicative of the mass of the stars involved. As suggested by the crowing of data points in Figure 3 and Figure 8, we could have divided these 30 stars into two sub-groups according to density. Since the NGC 6819 stars have density up to ![]() as a maximum value, we will not do such sub-divi- sion analysis, but would proceed to analyze other groups with different densities in the following sub-sections. Using the “raw data” in Table 2, we show the M- R relation in a log-log plot, giving a power index of 1.0612. The deduction is not very accurate, as expected, since the model is rather crude; however the analysis provides a modality to analyze stellar properties.
as a maximum value, we will not do such sub-divi- sion analysis, but would proceed to analyze other groups with different densities in the following sub-sections. Using the “raw data” in Table 2, we show the M- R relation in a log-log plot, giving a power index of 1.0612. The deduction is not very accurate, as expected, since the model is rather crude; however the analysis provides a modality to analyze stellar properties.
6.3. Low to-Mid Mass Main Sequence Stars
We follow up to study the B - P graph for Low-to-Mid mass main sequence stars. Parameters mass![]() , period of rotation P are obtained from the data published in [45] [46] , with radius deduced using the equation in [44] . Other relevant data calculated are entered into Table 3. Figure 9 gives us the power index is
, period of rotation P are obtained from the data published in [45] [46] , with radius deduced using the equation in [44] . Other relevant data calculated are entered into Table 3. Figure 9 gives us the power index is![]() , and Equation (6.1.1) for this group becomes
, and Equation (6.1.1) for this group becomes
![]() (6.3.1)
(6.3.1)
Following the argument of the previous sub-section, we can take that the function
![]() (6.3.2)
(6.3.2)
is approximately constant, and the above equation gives ![]() , resulting
, resulting
![]() (6.3.3a)
(6.3.3a)
![]() (6.3.3b)
(6.3.3b)
Since the M vs R plot is a good straight line with positive slope β = 1.0985(Figure 10), we can write (6.3.3b) as
![]() (6.3.4)
(6.3.4)
We require
![]()
Or
![]() (6.3.5)
(6.3.5)
If one plots the P-R graph (not shown here), the line of best fit has a very large positive slope(specified by angle![]() ), in line with our theoretical result of tan
), in line with our theoretical result of tan ![]() in our text above. We calculate, using experimental raw data from Table 3, the quantity A of (6.3.5) and plot it against the number of stars in this
in our text above. We calculate, using experimental raw data from Table 3, the quantity A of (6.3.5) and plot it against the number of stars in this
![]()
Figure 9. Employing values in Table 3, theoretically deduced equatorial dipolar magnetic field B (eq, Gauss) against rotation period ![]() of twelve Low-to-Mid Mass main sequence stars. The power index is
of twelve Low-to-Mid Mass main sequence stars. The power index is![]() .
.
![]()
Figure 10. The measured variation of mass M (kg) with respect to change of radius R of some members of the Low-to-Mid Mass main sequence stars (see Table 3). The power index is about 1.0985 here, as compared to the theoretical prediction value of 1.1; see details in Section (5). The maximum of the horizontal axis is![]() .
.
group in the following Figure 11. The constant A for 12 stars with ![]() . Thus, with the power index having the units of s/m, we have deduced an explicit relation between R and P for the Low-to-Mid mass main sequence stars:
. Thus, with the power index having the units of s/m, we have deduced an explicit relation between R and P for the Low-to-Mid mass main sequence stars:
![]() (6.3.6)
(6.3.6)
With the establishment of (6.3.6), we also deduce that
![]() (6.3.7)
(6.3.7)
Likewise, we obtain
![]() (6.3.8)
(6.3.8)
![]() (6.3.9)
(6.3.9)
The result of Equation (6.3.9) is shown in Figure 12. Note that as explained in Section (2.3), the void radius Ro and hence current loop size depends also the type of elements generated in the matter shell at the time of observation.
![]()
Figure 12. Employing values in Table 3, theoretically deduced equatorial dipolar magnetic field B (Gauss) against void radius ![]() of twelve Low-to-Mid Mass main sequence stars, with relatively good correlation.
of twelve Low-to-Mid Mass main sequence stars, with relatively good correlation.
Among this group of stars, we cannot expect all the star samples are built of hydrogen only. Thus the correlation of 0.83 in Figure 12 refelects the stated variation, and in our opinion, such correlation is already high in astronomy studies.
6.4. M34 Stars
M34 stars are pre-dwarfs having mass density slightly greater than that discussed in the last sub-section. Basic data are taken from [47] and other relevant variables are calculated and listed in Table 4. Taking M34 stars within a mass density range of ![]() from Table 4, we plot the B-P graph in Figure 13. The slope is −0.915. Putting the equation
from Table 4, we plot the B-P graph in Figure 13. The slope is −0.915. Putting the equation ![]() into Equation (6.1.1), we arrive at
into Equation (6.1.1), we arrive at
![]() (6.4.1)
(6.4.1)
Using raw data from Table 4, the M-R relation is shown in Figure 14, giving a slope of 0.9169. Substituting equation ![]() into Equation (6.4.1), we get
into Equation (6.4.1), we get
![]() (6.4.2)
(6.4.2)
So far, we can say that Equation (6.4.2) is a consequence of the derived Equation (6.1.1) with input of raw data. The P-R plot in log scale (Figure not shown) from raw data shows a slope of ~5, supporting Equation (6.4.2) though the
*this datum was observed under poor condition.
![]()
Figure 13. The equatorial magnetic field B (eq, Gauss) vs ![]() for 12 examples of M34 stars (within the density range of
for 12 examples of M34 stars (within the density range of![]() ) using data in Table 4 [47] . The slope is-0.915 for these pre-dwarf stars.
) using data in Table 4 [47] . The slope is-0.915 for these pre-dwarf stars.
![]()
Figure 14. Mass vs radius of 12 pre-Dwarfs of the M34 group within a rather wide mass density of![]() . The slope is 0.9169. The limit of the horizontal axis is
. The slope is 0.9169. The limit of the horizontal axis is![]() .
.
points are relatively scattered, due to large variation of the mass density among these samples. Just as that demonstrated in the last sub-section, if we have enough samples of narrow density range, the agreement between theory and measured result would be much better. Following, we plot the D-R graph in Figure 15. The negative slope indicates that the smaller the star, the higher the density, implying that in the star group more elements are formed in smaller sized stars, increasing the gravity force which leads to a smaller radius. This feature is characteristic of pre-Dwarfs and Dwarfs.
6.5. Averages of 254 Stars in the NGC 2516 Group
NGC 2516 is an open star cluster in the southern sky, also called Southern Beehive [48] . Following the same method as in other groups, basic data are taken from [49] and other variables are calculated, listed in Table 5. The B-P graph indicated in Figure 16 can be represented by the equation
![]() (6.5.1)
(6.5.1)
Substituting Equation (6.5.1) into (6.1.1), we have,
![]() (6.5.2)
(6.5.2)
This function F5 has been found numerically to be ![]() (SI units) for the five sets of averages of totally 254 stars, and we assume F5 to be a constant in our rough estimation, so that
(SI units) for the five sets of averages of totally 254 stars, and we assume F5 to be a constant in our rough estimation, so that
![]() (6.5.3)
(6.5.3)
which becomes
![]()
Or
![]() (6.5.4)
(6.5.4)
From (6.5.3) & (6.5.4), we obtain an equation relating M and P resulting from theory (with information from basic data only):
![]() (6.5.5)
(6.5.5)
![]()
Figure 15. Mass density vs radius of the same 12 pre-dwarfs M34 (as in Figure 14) within a wide range of density. The maximum of the horizontal axis is![]() .
.
![]()
Figure 16. 254 Low massstars in NGC 2516. The equatorial magnetic fields B (eq, Gauss) is plotted against the period of rotation ![]() using the data in Table 5 (from [49] ). The slope is minus 0.89.
using the data in Table 5 (from [49] ). The slope is minus 0.89.
We use the basic data from Table 5 to plot the P-R graph &M-R relation in Figure 17 and Figure 18 respectively; these graphs have power indices of 3.3721 &1.349 respectively. The agreement of the M-R relation between theory and experiment (1.37 vs 1.349) is amazingly close, noting that only three significant figures have been used in computation.
In the following Figure 19, we show the dependence of B (eq, theory, Gauss) on void radius![]() , showing a slope of 3.718 in the log-log plot. In Figure 20 we show the
, showing a slope of 3.718 in the log-log plot. In Figure 20 we show the ![]() graph. Note that within this D range, when D increases
graph. Note that within this D range, when D increases ![]() still increases with it, implying that gravity contraction has not been effective in these 254 stars. We also see that the power index in the M-R plot in
still increases with it, implying that gravity contraction has not been effective in these 254 stars. We also see that the power index in the M-R plot in
Figure 18 is relatively large, being 1.3487, suggesting material is being added on the star with M& R increasing at the same time. It is interesting to note that the power index is only 0.4123. We expect for Dwarfs, such an index in the ![]() would turn over to negative values.
would turn over to negative values.
6.6. Brown Dwarfs with Effectively 1353 Star Data
Nine sets of raw data, each representing an average of 150 stars are entered into Table 6. Effectively we have averages of 1350 brown dwarfs. In addition, we add another three sets of data for three brown dwarfs with relative fast rotation speeds according to ref [50] [51] [52] and [36] .
As shown in Figure 21, the power index ![]() is −0.96, and following the same procedure in analysis, we arrive at an equation for these brown dwarf samples:
is −0.96, and following the same procedure in analysis, we arrive at an equation for these brown dwarf samples:
![]() (6.6.1)
(6.6.1)
This constant F is found to be about ![]() (SI units).Similarly, we write (6.6.1) as
(SI units).Similarly, we write (6.6.1) as
![]() (6.6.2)
(6.6.2)
which becomes
![]()
Figure 18. Mass ![]() versus Radius
versus Radius ![]() of 254 low mass stars in the NGC 2516 based on “raw data” listed in Table 5. The slope is 1.3487 with excellent correlation. The theoretically predicted value is 1.37 (see Equation (6.5.5)).
of 254 low mass stars in the NGC 2516 based on “raw data” listed in Table 5. The slope is 1.3487 with excellent correlation. The theoretically predicted value is 1.37 (see Equation (6.5.5)).
![]()
Figure 19. 254 Low massstars in NGC 2516. The equatorial magnetic fields B (eq, Gauss) is plotted against the void radius ![]() using the data in Table 5 (from [49] ). The slope is about 3.72. The maximum of the horizontal axis is 2 ´ 106 m.
using the data in Table 5 (from [49] ). The slope is about 3.72. The maximum of the horizontal axis is 2 ´ 106 m.
![]()
Figure 20. The void radius Ro is plotted against the mass density D for the 254 stars in NGC 2516, represented by five averaged sets. Note that within this D range, when D increases Ro still increases with it, implying that gravity contraction has not been effective in these 254 stars. It is interesting to note that the power index is only 0.4123. We expect for Dwarfs, such an index in the![]() would turn over to negative values. The maximum of the horizontal axis is
would turn over to negative values. The maximum of the horizontal axis is![]() .
.
![]()
Figure 21. Employing values in Table 6, theoretically deduced equatorial dipolar magnetic field B (Gauss) against rotation period ![]() of 1350 Brown Dwarfs. Each of the set of 9 data points labelled BDL in Table 6 represents the average of 150 stars. The last three members in the same table, i.e. TVLM, J0036, J1835 are individual dwarfs as reported in [36] . B = 3.0 × 106 P−0.96…
of 1350 Brown Dwarfs. Each of the set of 9 data points labelled BDL in Table 6 represents the average of 150 stars. The last three members in the same table, i.e. TVLM, J0036, J1835 are individual dwarfs as reported in [36] . B = 3.0 × 106 P−0.96…
![]() (6.6.3a)
(6.6.3a)
Or
![]() (6.6.3b)
(6.6.3b)
Since the graph of log P against log R is linear with a slope of +2.4462 (see Figure 22), Equation (6.6.3b) can be expressed as
![]() (6.6.4)
(6.6.4)
under the constrain
![]() (6.6.5)
(6.6.5)
Or
![]() (6.6.6)
(6.6.6)
The log M versus log R plot in Figure 23 shows a slope of 1.185. The discrepancy is rather expected as the data points in the ![]() graphs are rather scattered, with only moderate correlation
graphs are rather scattered, with only moderate correlation![]() , implying the functional dependence among (M, R, P) is rather complicated. A relatively slight increase of the slope from 2.4462 to 2.91125 in the P―R graph would bring out a theoretical prediction of
, implying the functional dependence among (M, R, P) is rather complicated. A relatively slight increase of the slope from 2.4462 to 2.91125 in the P―R graph would bring out a theoretical prediction of![]() , identical to that obtained from basic data. The B (eq, theory, G) vs Ro/R graph is shown in Figure 24, as an illustration of the Law of Intrinsic Dipole Magnetic Field for Cool Stellar Objects, namely, expression (4.2.14). Note also that the theoretical pole field is twice the equatorial field, so the maximum surface field of Brown Dwarfs is within the kGauss range, as observed.
, identical to that obtained from basic data. The B (eq, theory, G) vs Ro/R graph is shown in Figure 24, as an illustration of the Law of Intrinsic Dipole Magnetic Field for Cool Stellar Objects, namely, expression (4.2.14). Note also that the theoretical pole field is twice the equatorial field, so the maximum surface field of Brown Dwarfs is within the kGauss range, as observed.
![]()
Figure 23. Using data in Table 6, we show the ![]() relation for 1350 Brown Dwarfs (represented by averages of 9 groups) plus three other individual ones. The slope is 1.1849.
relation for 1350 Brown Dwarfs (represented by averages of 9 groups) plus three other individual ones. The slope is 1.1849.
![]()
Figure 24. Surface equatorial field B (eq, theory, Gauss) vs the normalized void radius Ro/R for averages of 1353 Brown Dwarfs thin a rather wide range mass density as specified. This is an illustration of the Law of Intrinsic Dipole Magnetic Field for Cool Stellar Objects. The maximum value on the horizontal axis is 10−2. The slope is 3.0 as depicted in expression (4.2.14).
6.7. White Dwarfs
Basic data for a number of White Dwarfs are obtained from [53] [54] [55] . Other variables are calculated and entered into Table 7. Using sets of (B, P) values, we show in the usual way the B-P graph in Figure 25, finding the slope to be by![]() , and expression (6.1.1) becomes
, and expression (6.1.1) becomes
![]() (6.7.1)
(6.7.1)
We have found that numerically, as in other star groups the LHS of the following equation is an approximate constant:
![]() (6.7.2a)
(6.7.2a)
leading to
![]() (6.7.2b)
(6.7.2b)
Equation (6.7.2b) indicates that our theory predicts a large negative slope
![]()
Figure 25. Employing values in Table 7, theoretically deduced surface equatorial dipolar magnetic field B (eq, theory, Gauss) against rotation period ![]() of nine white dwarfs is shown above. The slope of this log-log plot is −0.705, with excellent correlation.
of nine white dwarfs is shown above. The slope of this log-log plot is −0.705, with excellent correlation.
![]() . Referring to Figure 26, the P-R plot based on “raw observational data” gives a very large magnitude of negative slope around −35. We have emphasized previously that the slopes of the P-R plot of some other star groups are positive. This “turning over” result is important in the stellar evolution process. When the mass density is high (in White dwarfs,
. Referring to Figure 26, the P-R plot based on “raw observational data” gives a very large magnitude of negative slope around −35. We have emphasized previously that the slopes of the P-R plot of some other star groups are positive. This “turning over” result is important in the stellar evolution process. When the mass density is high (in White dwarfs,![]() ), and the gravity force is much larger than those stars in all the groups discussed in Sections (6.1 - 6.6). Fusion proceeds slowly and the radius shrinks while rotation slows down with P increasing at a fast rate, like an aging organism, leading to a large negative slope in the P-R plot, as observed. Due to the inaccuracy of the measured values of R, the radius of a dwarf is usually calculated via the Hamada-
), and the gravity force is much larger than those stars in all the groups discussed in Sections (6.1 - 6.6). Fusion proceeds slowly and the radius shrinks while rotation slows down with P increasing at a fast rate, like an aging organism, leading to a large negative slope in the P-R plot, as observed. Due to the inaccuracy of the measured values of R, the radius of a dwarf is usually calculated via the Hamada-
![]()
Figure 26. Refer to Table 7. The period of rotation ![]() versus the radius
versus the radius ![]() in the log-log plot gives a very large magnitude of negative slope using the data for the 9 members collected. Note that the slopes of the P-R plot of some other star groups are positive. This “turning over” result is important in the stellar evolution process. When the mass density is high (such as in the White dwarfs,
in the log-log plot gives a very large magnitude of negative slope using the data for the 9 members collected. Note that the slopes of the P-R plot of some other star groups are positive. This “turning over” result is important in the stellar evolution process. When the mass density is high (such as in the White dwarfs, ![]() , and the gravity force is much larger than those stars in all the groups discussed in Sections (6.1 - 6.6)). Fusion proceeds slowly and the radius shrinks while rotation slows down with P increasing at a fast rate, like an aging organism, leading to a large negative slope in the P-R plot, as observed. Due to the inaccuracy of the measured values of R, it is difficult at this stage to obtain well defined power law relation. For stars at younger age, fusion processes bring in heavier elements, but the density is low so that the gravitation contraction cannot overcome centrifugal force, and positive slopes should result in the P-R plots, as observed experimentally. More detailed discussion requires the analysis of the variation of mass density mathematically as a function of R.
, and the gravity force is much larger than those stars in all the groups discussed in Sections (6.1 - 6.6)). Fusion proceeds slowly and the radius shrinks while rotation slows down with P increasing at a fast rate, like an aging organism, leading to a large negative slope in the P-R plot, as observed. Due to the inaccuracy of the measured values of R, it is difficult at this stage to obtain well defined power law relation. For stars at younger age, fusion processes bring in heavier elements, but the density is low so that the gravitation contraction cannot overcome centrifugal force, and positive slopes should result in the P-R plots, as observed experimentally. More detailed discussion requires the analysis of the variation of mass density mathematically as a function of R.
Salpeter relation for dwarfs for decades [41] . It is difficult at this stage to obtain well defined power law relation for the P-R relation with sample masses within a narrow range of![]() . Equation (6.7.2b) gives the rough estimation that
. Equation (6.7.2b) gives the rough estimation that ![]() constant, which is quite true approximately (see Table 7).
constant, which is quite true approximately (see Table 7).
In other words, expression (6.7.2b) becomes
![]() (6.7.2c)
(6.7.2c)
For stars at younger age, fusion processes bring in heavier elements, but the density is low so that the gravitation contraction cannot overcome centrifugal force, and positive slopes should result in the P-R plots, as observed experimentally. More detailed discussion requires the analysis of the variation of mass density mathematically as a function of R.
Employing data values in Table 7, theoretically deduced equatorial dipolar magnetic field B (eq, theory, G) vs the void radius ![]() under conditions governed by the Second law of Angular Momentum is shown in Figure 27. The slope is 2.81, with excellent correlation.
under conditions governed by the Second law of Angular Momentum is shown in Figure 27. The slope is 2.81, with excellent correlation. ![]() values are within a very narrow range. The magnetic dipole fields are within
values are within a very narrow range. The magnetic dipole fields are within ![]() Gauss. The order of magnitude of white dwarfs’ surface field is much of a debate even up to
Gauss. The order of magnitude of white dwarfs’ surface field is much of a debate even up to
![]()
Figure 27.Employing data values in Table 7, theoretically deduced equatorial dipolar magnetic field B (Gauss) against the void radius ![]() under conditions governed by the Second law of Angular Momentum. The slope is 2.81, with excellent correlation. We consider that the measured magnetic fields of white dwarfs are affected by the change in dynamics of the spinors inside the void during stellar evolution. The maximum of the horizontal axis is
under conditions governed by the Second law of Angular Momentum. The slope is 2.81, with excellent correlation. We consider that the measured magnetic fields of white dwarfs are affected by the change in dynamics of the spinors inside the void during stellar evolution. The maximum of the horizontal axis is![]() .
.
now. Some detect field~Tesla or more, and some measurements lead to the suggestion that while there are two types of White Dwarfs-one with negligible magnetic field and another type with huge magnetic field. We have devoted one short section on the plausible origin of the sporadic fields, explained in terms of Chern-Simon potential in Secction (5) already. Equations 6.7.2(a) & 6.7.2 (c) might be considered to be the two laws consequential to the new Equation (6.7.1) for White Dwarfs of low masses as stated.
6.8. Magnetic White Dwarfs
Taking 7 Magnetic Whit Dwarf (MWD) samples [40] [55] [56] with close mass density values, we plot the B-P graph in Figure 28, using data in Table 8. Now the slope of Figure 28 is![]() , and expression (6.1.1) becomes
, and expression (6.1.1) becomes
![]() (6.8.1)
(6.8.1)
Leading to;
![]() (6.8.2)
(6.8.2)
The function C1 for the seven members are respectively 319.864, 318.5664, 319.917, 318.75, 319.635, 319.16, 319.40. The average K1 is about 319.33 (see Figure 29).
Therefore (6.8.2) becomes
![]() (6.8.3a)
(6.8.3a)
Or
![]() (6.8.3b)
(6.8.3b)
Now the relation between Mass and radius is assumed to follow the model of Hamada and Salpeter. Using data in Table 8, we show the M-R graph in Figure 30 giving a slope of −1.159. Substituting therefore the following equation
![]() (6.8.4)
(6.8.4)
![]()
Figure 28. Employing values in Table 8, theoretically deduced equatorial dipolar magnetic field B (eq, theory, Gauss) against rotation period ![]() of seven magnetic white dwarfs of close mass density values. The slope of this log-log plot is −0.712, with excellent correlation.
of seven magnetic white dwarfs of close mass density values. The slope of this log-log plot is −0.712, with excellent correlation.
![]()
Figure 29. The values of the function C1 in Equation (6.8.2) are very close to a constant with a mean of 319.33 (SI units).
Into Equation (6.8.3b), we arrive at
![]() (6.8.5)
(6.8.5)
So far, we can consider that the theoretical Equation (6.8.1) leads to (6.8.5) using only the stated M-R relation, with input of “raw data”. When we plot ![]() vs
vs ![]() based on measured data (Figure not shown), the slope is negative and the magnitude is rather large, within a range −58 to −62, being consistent to Equation (6.8.5), though the data points are rather scattered.
based on measured data (Figure not shown), the slope is negative and the magnitude is rather large, within a range −58 to −62, being consistent to Equation (6.8.5), though the data points are rather scattered.
We show the relation between the void radius ![]() and mass density D in Figure 31. Clearly, we theorize that if the mass densities of some MWD are larger, the gravitation forces are larger in these stars, leading to smaller void sizes.
and mass density D in Figure 31. Clearly, we theorize that if the mass densities of some MWD are larger, the gravitation forces are larger in these stars, leading to smaller void sizes.
![]()
Figure 30. Mass ![]() vs radius
vs radius ![]() for 7 magnetic white dwarfs. Linear scaling gives a better presentation, giving a power index of −1.159.
for 7 magnetic white dwarfs. Linear scaling gives a better presentation, giving a power index of −1.159.
![]()
Figure 31. The relation between the void radius ![]() and mass density D. We theorize that if the mass densities of some MWD are larger, the gravitation forces are larger in these stars, leading to smaller void sizes. The slope of the graph is −3.547. The maximum of the horizontal axis is
and mass density D. We theorize that if the mass densities of some MWD are larger, the gravitation forces are larger in these stars, leading to smaller void sizes. The slope of the graph is −3.547. The maximum of the horizontal axis is![]() .
.
7. General Discussion and Summary
7.1. The Mystery of the Relationship between Surface Magnetic Field and Equatorial Rotational Speed of Stars
It is well known that the three groups of Zeeman components, ![]() , and
, and ![]() of spectral lines (such as a Calcium line), are characterized by different magnetic moments, leading to three distinctive polarization states of these components. The polarization states of electromagnetic waves can be determined by measuring all the four Stokes parameters I, Q, U, V of these waves received. Here Stokes parameter I represents the integrated light intensity (unpolarized light), Stokes parameters Q and U measure the two orthogonal directions of li- near polarization, and Stokes parameter V measures circular polarization(for practical detection of polarization of radio waves from a star, see [57] ). The “longitudinal magnetic field
of spectral lines (such as a Calcium line), are characterized by different magnetic moments, leading to three distinctive polarization states of these components. The polarization states of electromagnetic waves can be determined by measuring all the four Stokes parameters I, Q, U, V of these waves received. Here Stokes parameter I represents the integrated light intensity (unpolarized light), Stokes parameters Q and U measure the two orthogonal directions of li- near polarization, and Stokes parameter V measures circular polarization(for practical detection of polarization of radio waves from a star, see [57] ). The “longitudinal magnetic field![]() ”or the “mean line-of-sight magnetic field” is a line intensity weighted average (over the visible hemisphere of a star) of the magnetic field component directed along the line of-sight. In practice, it is obtained from measuring the separation between the positions of the spectral line profiles in the detected left and right circularly polarized light. However, the angle i between the line of sight and the magnetic axis of a star is usually unknown unless under very special circumstances (see e.g. Techniques for stellar magnetic field measurements, [58] and [59] ). Moreover, the polarization states (or the Stokes parameters) are transferred and are changed during the passage of the waves through the intervening plasma between the star and the point of observation [60] [61] [62] . The characteristics of the plasma are generally not known for a distant star and another source of errors can be introduced in the interpretation.
”or the “mean line-of-sight magnetic field” is a line intensity weighted average (over the visible hemisphere of a star) of the magnetic field component directed along the line of-sight. In practice, it is obtained from measuring the separation between the positions of the spectral line profiles in the detected left and right circularly polarized light. However, the angle i between the line of sight and the magnetic axis of a star is usually unknown unless under very special circumstances (see e.g. Techniques for stellar magnetic field measurements, [58] and [59] ). Moreover, the polarization states (or the Stokes parameters) are transferred and are changed during the passage of the waves through the intervening plasma between the star and the point of observation [60] [61] [62] . The characteristics of the plasma are generally not known for a distant star and another source of errors can be introduced in the interpretation.
On the other hand, measuring directly the features of Zeeman splitting in stellar spectral lines offers another method of detection of surface magnetic field strength of a star. However, such method, which in principle, should give more accurate surface magnetic fields, is limited to field strength greater than ![]() kG, and rotation period smaller than
kG, and rotation period smaller than ![]() based on discussion in [63] and our estimation. We would also remark that in addition to a dipole field, stars (such as the sun) could have flares which carry magnetic fields much stronger than the “intrinsic” dipole field, though the total area of the flare regions in the photosphere is much smaller than the surface of the visible disc. Thus during the quiescent time period, or in older stars,
based on discussion in [63] and our estimation. We would also remark that in addition to a dipole field, stars (such as the sun) could have flares which carry magnetic fields much stronger than the “intrinsic” dipole field, though the total area of the flare regions in the photosphere is much smaller than the surface of the visible disc. Thus during the quiescent time period, or in older stars, ![]() or mean surface B has a value close to the equatorial dipole field of a star. During the magnetically active periods, or in younger stars which might have less magnetic activities, the measured average field might fall between the equatorial and the polar field (which is simply twice the equatorial field)or close to the polar field. Moreover, If cyclotron radiation is observed in the emission from a target star/stellar object (see e.g. application of such radiation mechanism, including the maser effect, to explain the radio emissions from the sun and planet Jupiter already half a century ago [64] [65] ), and if the polarization is close to circular, one can calculate the magnetic field at the source readily. Such a method has been applied to estimate the surface magnetic field of some Brown Dwarfs recently [36] . However, the maser effect of such emissions does not tell us which harmonic(s) carries the dominant radiative power and there could be a difference of factor
or mean surface B has a value close to the equatorial dipole field of a star. During the magnetically active periods, or in younger stars which might have less magnetic activities, the measured average field might fall between the equatorial and the polar field (which is simply twice the equatorial field)or close to the polar field. Moreover, If cyclotron radiation is observed in the emission from a target star/stellar object (see e.g. application of such radiation mechanism, including the maser effect, to explain the radio emissions from the sun and planet Jupiter already half a century ago [64] [65] ), and if the polarization is close to circular, one can calculate the magnetic field at the source readily. Such a method has been applied to estimate the surface magnetic field of some Brown Dwarfs recently [36] . However, the maser effect of such emissions does not tell us which harmonic(s) carries the dominant radiative power and there could be a difference of factor ![]() in the estimation. Since the star is moving with respect to the observer, in general, there is error due to Doppler broadening. Therefore the “measured
in the estimation. Since the star is moving with respect to the observer, in general, there is error due to Doppler broadening. Therefore the “measured ![]() value” or mean surface magnetic field can only be taken to be an order of magnetic field estimation when compared with the theory. In general, the measured field is larger than the predicted dipole field. Nevertheless, the measured magnetic fields reported in literature provide certain trends, relative variation among star groups which are important for our understanding of stellar evolution. Note that the rotational period of a star is commonly taken to be represented by
value” or mean surface magnetic field can only be taken to be an order of magnetic field estimation when compared with the theory. In general, the measured field is larger than the predicted dipole field. Nevertheless, the measured magnetic fields reported in literature provide certain trends, relative variation among star groups which are important for our understanding of stellar evolution. Note that the rotational period of a star is commonly taken to be represented by![]() .
.
We have analyzed the B (equatorial, theory) ?P relation for 8 groups of stars in the last section. Experimentally, it has long been discovered that the mean projected rotational velocity ![]() of main-sequence stars increases slowly with type, reaching a maximum of about
of main-sequence stars increases slowly with type, reaching a maximum of about ![]() in the late-B star class (see [66] or earlier works of Abt & Hunter). Reiners [67] found out that there was a linear relation between the averaged magnetic field and rotation speed in log scale (see Figure 21 of that paper). A rough estimation shows the slope to be around
in the late-B star class (see [66] or earlier works of Abt & Hunter). Reiners [67] found out that there was a linear relation between the averaged magnetic field and rotation speed in log scale (see Figure 21 of that paper). A rough estimation shows the slope to be around ![]() Note that the inverse of the rotational speed v is proportional to the rotational period P. As demonstrated there, such a B-P relation is sensitive to change of mass density. We therefore attempt to compare the theoretical consequence and the measured magnetic field in one group of stars with relative larger star number (than we have employed in Section (6) for various stellar groups), particularly when age information is available. Before we do that, let us introduce some relevant background for further analysis.
Note that the inverse of the rotational speed v is proportional to the rotational period P. As demonstrated there, such a B-P relation is sensitive to change of mass density. We therefore attempt to compare the theoretical consequence and the measured magnetic field in one group of stars with relative larger star number (than we have employed in Section (6) for various stellar groups), particularly when age information is available. Before we do that, let us introduce some relevant background for further analysis.
Blackett found a positive correlation between the magnetic moment ![]() and angular momentum of the Earth, Sun and an A2p star 78 Virgins, and proposed that such a relation might be a fundamental a law (see discussion in [68] ). Later studies coined this correlation as the “Magnetic Bode’s Law” (see e.g. [69] ). This law can be stated as log (magnetic moment as represented by
and angular momentum of the Earth, Sun and an A2p star 78 Virgins, and proposed that such a relation might be a fundamental a law (see discussion in [68] ). Later studies coined this correlation as the “Magnetic Bode’s Law” (see e.g. [69] ). This law can be stated as log (magnetic moment as represented by![]() ) vs log (angular momentum
) vs log (angular momentum![]() ) has an approximate linear relation for many stars; here B is the equatorial magnetic. Though we consider the application of this law to planets is unconvincing, such investigation opens up an interesting and important issue. First we would note that a magnet experiences a torque
) has an approximate linear relation for many stars; here B is the equatorial magnetic. Though we consider the application of this law to planets is unconvincing, such investigation opens up an interesting and important issue. First we would note that a magnet experiences a torque ![]() in the presence of a magnetic field B and the magnetic moment
in the presence of a magnetic field B and the magnetic moment ![]() is defined as the maximum torque
is defined as the maximum torque ![]() experienced by the magnet, satisfying
experienced by the magnet, satisfying![]() . The SI unit is
. The SI unit is![]() . When a current I flows around a plane coil of (vector) area A, this coil also experiences a torque
. When a current I flows around a plane coil of (vector) area A, this coil also experiences a torque![]() . The unit is Ampere
. The unit is Ampere![]() . In the study of stellar magnetism, consider the magnetic field to be produced by a current loop. Measured at a far distance r, as in our case, the magnetic moment of the star is related to the magnetic field by
. In the study of stellar magnetism, consider the magnetic field to be produced by a current loop. Measured at a far distance r, as in our case, the magnetic moment of the star is related to the magnetic field by![]() . Thus the magnetic moment is
. Thus the magnetic moment is![]() . Hence,
. Hence, ![]() with a unit of
with a unit of ![]() or
or ![]() does not have the right unit as magnetic moment and might be mis-interpreted when physical concept is involved in our series of works. We would therefore call “
does not have the right unit as magnetic moment and might be mis-interpreted when physical concept is involved in our series of works. We would therefore call “![]() ” as a magnetic parameter in our analysis to follow.
” as a magnetic parameter in our analysis to follow.
Now if the “magnetic Bode’s Law” is established, two important issues emerge: (i) Since an electric current or permanent magnet must exist to generate a magnetic field, it is of fundamental interest in physics to know how the Maxwell equations are “hidden behind”/within the magnetic Bode’s law; (ii) On the application side, variables in magnetism (magnetic field, flux) can be calculated from variables of mechanics (period of rotation, radius, mass) and vice versa if only one is unknown; (iii) Various models of dynamo theories have been proposed to explain the source of dipolar field and sporadic fields of stars. We note that long ago, using over ten thousand spot samples, it has been shown, using rather stringent statistics (the Maximum-likelihood analysis) that there is no statistical evidence that sunspots in the northern hemisphere and southern hemisphere are correlated [70] . This result supports the theory that the solar flare phenomenon is more likely to be associated with local variations.
In 1996, Baliunas, et al. reported the values of measured magnetic fields of 112 low main sequence stars (type F to late K with one M) [71] by analyzing features of the spectral lines arising from Zeeman splitting mentioned earlier, carried over 25 years at Mount Wilson Observatory. The rotation periods of 80 stars were inferred from periodic fluctuations with the stated Ca II records; for the other 32 stars, rotation was computed from the close relation between Ca II flux and the Rossby number (see details of Rossby number in [72] ) in order to reduce the errors due to the unknown values of the angle i between the magnetic axis of rotation and the line of sight. The authors employ a quantity RHK’ (called magnetic heating parameter) to approximate the magnetic moment µm and presented the ![]() graph, indicating a linear relation with a slope of about 0.6 (see Figure 1 of [66] ) with rather narrow spread in astronomical sale. Among the 112 stars under studied, the surface magnetic fields
graph, indicating a linear relation with a slope of about 0.6 (see Figure 1 of [66] ) with rather narrow spread in astronomical sale. Among the 112 stars under studied, the surface magnetic fields ![]() of 13 members were published in [73] . Defining
of 13 members were published in [73] . Defining ![]() as magnetic moment of a star, it was reported that the
as magnetic moment of a star, it was reported that the ![]() graph also shows a linear relationship with a slope of 0.54.The above review and analysis indicates that in order to explain the Magnetic Bode’s Law, one has to assume that there is no need to have information about the current in the matter star; in that case one has to look for the “missing electric current” (or the hidden Maxwell equations) which generates the magnetic field. If one assumes dynamo models do exist in reality to explain the emergence of magnetic field, it is hard to believe that with so many variable conditions occurring in the matter structures of different stars, a rather general
graph also shows a linear relationship with a slope of 0.54.The above review and analysis indicates that in order to explain the Magnetic Bode’s Law, one has to assume that there is no need to have information about the current in the matter star; in that case one has to look for the “missing electric current” (or the hidden Maxwell equations) which generates the magnetic field. If one assumes dynamo models do exist in reality to explain the emergence of magnetic field, it is hard to believe that with so many variable conditions occurring in the matter structures of different stars, a rather general ![]() and B-P relations in the log-log plot occurs for a large number of cool stars. In this paper, we have already derived an explicit expression for the dipolar magnetic field of stellar objects in terms of only the basic data set (M, R, P).
and B-P relations in the log-log plot occurs for a large number of cool stars. In this paper, we have already derived an explicit expression for the dipolar magnetic field of stellar objects in terms of only the basic data set (M, R, P).
It is therefore fruitful to compare our theoretical prediction with measured data within one main star type with more samples than in the last section.
Incidentally, more recently, Marsden et al. [74] compiled a rather comprehensive survey of the data of 170 sun-like stars, providing the measured “longitudinal surface magnetic field![]() ” as defined above, mass, radius,
” as defined above, mass, radius, ![]() , age of these stars. Though limited by the methodology of measurement as mentioned above in Stokes parameter analysis and the error involved in the angle of sight i (and hence the period of rotation P), so that the uncertainties of B(we will use the symbol B to replace
, age of these stars. Though limited by the methodology of measurement as mentioned above in Stokes parameter analysis and the error involved in the angle of sight i (and hence the period of rotation P), so that the uncertainties of B(we will use the symbol B to replace![]() ) field and P can be 100 % or more in practical cases, yet we can still take these data to investigate the
) field and P can be 100 % or more in practical cases, yet we can still take these data to investigate the ![]() relation based on our 5D theory and compared with the measured data, as a beginning step for comparison of theoretical result and experimental data. In Table 9, we list the data relevant to this study with examples taken from [74] . The mass density is calculated based on the simple model of
relation based on our 5D theory and compared with the measured data, as a beginning step for comparison of theoretical result and experimental data. In Table 9, we list the data relevant to this study with examples taken from [74] . The mass density is calculated based on the simple model of![]() . This is a rough estimation because in a sun-like star, most of the matter is in a plasma state, and at different depth, the rotation rates are different for any single star, so that the D is the average, and the angular momentum thus calculated, based on the “solid” model will inevitably introduce significant errors in magnitudes in the next step of our analysis.
. This is a rough estimation because in a sun-like star, most of the matter is in a plasma state, and at different depth, the rotation rates are different for any single star, so that the D is the average, and the angular momentum thus calculated, based on the “solid” model will inevitably introduce significant errors in magnitudes in the next step of our analysis.
7.2. Comparison between Theoretical Deduced Surface Magnetic Fields and Measured Values for Sun-Like Stars with Age Smaller Than about 3 Gyr
Since the magnetic field measured is the average surface “longitudinal” field, we use the polar magnetic field derived from our theory in Section (5), which is simply twice the equatorial field, and plot the dependent variable B (polar, theory, G) in Gauss against the measured ![]() for two ranges of density (points in red are within the density range of
for two ranges of density (points in red are within the density range of![]() ; points in light red are within the density range of 900 to ~
; points in light red are within the density range of 900 to ~![]() ) in Figure 32 below. We used polar rather than equatorial fields because we expect more extra-dipole magnetic activity in younger stars, as explained above in this section. The power indices are respectively 0.5506 & 0.5563 in this graph. Note that in Figure 21 of [74] the power index is around 1.0; the magnetic fields of those stars are in general one order of magnitude higher. We anticipate that those stars have higher mass densities than the ones in this diagram, and conclude that the slope of the log-log lot gradual increases as the mass density enlarges. Putting the measured data (represented by triangles points in Table 9(a)) into Figure 32, we have Figure 33, demonstrating that the experimental and theoretical results are consistent within an order of magnitude.
) in Figure 32 below. We used polar rather than equatorial fields because we expect more extra-dipole magnetic activity in younger stars, as explained above in this section. The power indices are respectively 0.5506 & 0.5563 in this graph. Note that in Figure 21 of [74] the power index is around 1.0; the magnetic fields of those stars are in general one order of magnitude higher. We anticipate that those stars have higher mass densities than the ones in this diagram, and conclude that the slope of the log-log lot gradual increases as the mass density enlarges. Putting the measured data (represented by triangles points in Table 9(a)) into Figure 32, we have Figure 33, demonstrating that the experimental and theoretical results are consistent within an order of magnitude.
One can use the “raw data” and plot the mass vs radius graph, for sun-like stars with density in the range ![]() (deep blue) and in the range
(deep blue) and in the range ![]() (light blue). These stars are young ones with ages
(light blue). These stars are young ones with ages![]() . The relation is not simple- roughly power law for the higher density ones and a polynomial for the lower density stars. We do not show this graph but note that with changing density, the M-R relation varies.
. The relation is not simple- roughly power law for the higher density ones and a polynomial for the lower density stars. We do not show this graph but note that with changing density, the M-R relation varies.
In Figure 34, the theoretically derived polar magnetic field is plotted against the period of rotation ![]() for a group of sun-like stars within the density range of
for a group of sun-like stars within the density range of![]() , in red color. The other sub-group in light red represents those within the density range of
, in red color. The other sub-group in light red represents those within the density range of![]() . The power indices are respectively −0.741 and −0.716, close to the values deduced in
. The power indices are respectively −0.741 and −0.716, close to the values deduced in
(a) ![]() (b)
(b) ![]()
Table 9. (a) Young Sun-like stars. Entry numbers in columns 1, 2, 3, 4, 5, 7 are taken directly from [74] and entries of other columns are deduced or calculated based on the present theory. When the age information is not available (N), raw data are still used if ![]() is greater than or around
is greater than or around![]() ; (b) Old sun-like stars. Entry numbers in columns 1, 2, 3, 4, 5, 7 are taken directly from [74] and entries of other columns are deduced or calculated based on the present theory. If the age information is not available (N), raw data are still used (as transition stars) if
; (b) Old sun-like stars. Entry numbers in columns 1, 2, 3, 4, 5, 7 are taken directly from [74] and entries of other columns are deduced or calculated based on the present theory. If the age information is not available (N), raw data are still used (as transition stars) if ![]() is smaller than or around
is smaller than or around![]() .
. ![]() about equals to
about equals to ![]() is taken as the boundary between young and old sun-like stars.
is taken as the boundary between young and old sun-like stars.
![]()
Figure 33. Putting the measured data based on Table 9(a) into Figure 32, we have Figure 33 above, showing that the experimental result (triangles; the deep/light blue ones pertain to the higher/lower density groups respective) and theoretical prediction (circles) are rather close in astronomical estimation. The power indices of the two straight lines are respectively 0.5506(deep reed) & 0.5563 (light red). The correlation coefficients are already specified in Figure 32.
the last section for other star groups. Putting the measured data listed in Table 9(a) into Figure 34, we arrive at Figure 35, and we observe that both the measured (triangles) and theoretical (circles) magnetic fields decrease with increasing P with the same general trend.
The only parameter value we have assumed, based on the argument explained twice before, is the Fermi energy of the spinor to be equal to the rest mass of electron. The cool stars considered in this sub-section and the next is similar to the regime of the Second Law of angular momentum we derived in [2] and this paper.
Now we proceed to analyze the relation between the magnetic parameter ![]() and the angular momentum. In Figure 36 we present the graph with the magnetic parameter
and the angular momentum. In Figure 36 we present the graph with the magnetic parameter ![]() vs the angular momentum of a group of sun-like stars with age around and below 3 Gyr. The triangles are the measured values (deeper blue for density greater than
vs the angular momentum of a group of sun-like stars with age around and below 3 Gyr. The triangles are the measured values (deeper blue for density greater than![]() , and light blue ones pertain to density below
, and light blue ones pertain to density below![]() . The circles represent points that are derived and calculated from the theory of Section (4), using the measured values of (M, R, P). Deep red ones have densities in the range
. The circles represent points that are derived and calculated from the theory of Section (4), using the measured values of (M, R, P). Deep red ones have densities in the range ![]() and the light red ones have densities between
and the light red ones have densities between![]() , as in other figures. The straight line threads through the theoretical equatorial field “calculated points”, and the upper circular points pertain to the polar fields of the same stars. From the graph, the average of the measured data falls in between these two trends, having about the same slope of 0.75.
, as in other figures. The straight line threads through the theoretical equatorial field “calculated points”, and the upper circular points pertain to the polar fields of the same stars. From the graph, the average of the measured data falls in between these two trends, having about the same slope of 0.75.
![]()
Figure 35. Putting the measured data as listed in Table 9(a) into Figure 34, we obtain the above graph, showing that both the measured (triangles; the deep/light blue ones pertain to the higher/lower density groups respective) and theoretical polar magnetic fields (circles) decrease with increasing P. The power indices of the two straight lines are respectively-0.741 (deep reed) &−0.716 (light red). The correlation coefficients are already specified in Figure 34.
7.3. Comparison between Theoretical Deduced Surface Magnetic Fields and Measured Values for Old Sun-Like Stars with Age Greater Than about 3 Gyr
We will not take too much space to indicate all graphs above for the older sun- like stars, because there is high similarity in some. Based on data listed in Table 9(b), in Figure 37, we present the relevant graphs that are related to our discussion--Mass vs radius of sun-like stars with age between ~3 and 13 Gyr. The red triangles represent those with mass density between 1.0 to 2.5 times ![]() and the purple ones have densities below
and the purple ones have densities below![]() . The definition of young and old is arbitrary; therefore there is one star appearing both the old and young graphs for the transition. The data are all experimentally measured with various methodologies for different variables of the data set (M,R,P).The power index is 0.4649 for the high density ones, where it is 0.3391 for the low density ones; the correlation is not excellent, but good enough to show an important natural aspect in stellar evolution: as this group of stars ages, the mass does not decrease, implying that matter is being continuously generated, with increase in size of the star, but keeping a lower mass density. Note that the sun has been predicted to become a red giant.
. The definition of young and old is arbitrary; therefore there is one star appearing both the old and young graphs for the transition. The data are all experimentally measured with various methodologies for different variables of the data set (M,R,P).The power index is 0.4649 for the high density ones, where it is 0.3391 for the low density ones; the correlation is not excellent, but good enough to show an important natural aspect in stellar evolution: as this group of stars ages, the mass does not decrease, implying that matter is being continuously generated, with increase in size of the star, but keeping a lower mass density. Note that the sun has been predicted to become a red giant.
![]()
Figure 37. Mass vs radius of sun-like stars with age between ~3 and 13 Gyr. The red triangles represent those with mass density between 1.0 to 2.5 times ![]() and the purple ones have densities below
and the purple ones have densities below![]() . The definition of young and old is arbitrary; therefore there is one star appearing in both the old and young graphs for the transition. The data are all experimental measured with various methodologies for different variables of the data set (M, R, P). The power index is 0.4649 for the high density ones, where it is 0.3391 for the low density ones; the correlation is not excellent, but good enough to show an important natural aspect in stellar evolution: as this group of stars ages, the mass does not decrease, implying matter is being continuously generated, with increase in size of star, but keeping a lower mass density. We cannot follow the stellar evolution as the data are associated with different groups in location. There are forty star samples there, but many are overlapping in the middle. The trend is obvious from Physics, because the mass is around one solar mass, below the Chandrasekhar limit, and the gravitational attraction cannot overcome the centrifugal force, though the rotation speed is slowing down. The upper limit of the vertical axis is
. The definition of young and old is arbitrary; therefore there is one star appearing in both the old and young graphs for the transition. The data are all experimental measured with various methodologies for different variables of the data set (M, R, P). The power index is 0.4649 for the high density ones, where it is 0.3391 for the low density ones; the correlation is not excellent, but good enough to show an important natural aspect in stellar evolution: as this group of stars ages, the mass does not decrease, implying matter is being continuously generated, with increase in size of star, but keeping a lower mass density. We cannot follow the stellar evolution as the data are associated with different groups in location. There are forty star samples there, but many are overlapping in the middle. The trend is obvious from Physics, because the mass is around one solar mass, below the Chandrasekhar limit, and the gravitational attraction cannot overcome the centrifugal force, though the rotation speed is slowing down. The upper limit of the vertical axis is![]() .
.
The variation of the theoretical equatorial fields of old sun-like stars with changing P is demonstrated in Figure 38(a). The red circles represent those stars with mass density in the range ![]() and
and![]() . The pink ones pertain to density in the range from several hundred
. The pink ones pertain to density in the range from several hundred ![]() to
to![]() . Notice that for the young star group, the slopes are very close, but the slopes for the old stars are sensitive to change in density. This is expected as there is a significant change in star radius as a star evolves in its old age, in this sun-like group. Having identified the slopes for the relatively high and low density subgroups of the old stars, we can put the theoretical equatorial fields together in Figure 38(b). The pink circles now represent the old stars with mass density in the whole range from several hundred
. Notice that for the young star group, the slopes are very close, but the slopes for the old stars are sensitive to change in density. This is expected as there is a significant change in star radius as a star evolves in its old age, in this sun-like group. Having identified the slopes for the relatively high and low density subgroups of the old stars, we can put the theoretical equatorial fields together in Figure 38(b). The pink circles now represent the old stars with mass density in the whole range from several hundred ![]() to
to![]() . The averaged slope obtained here is in line with the B-P plots of other groups such as NGC 6819, low-to-mid mass main sequence stars plus others, showing slopes around −0.75, as analyzed earlier in the previous section.
. The averaged slope obtained here is in line with the B-P plots of other groups such as NGC 6819, low-to-mid mass main sequence stars plus others, showing slopes around −0.75, as analyzed earlier in the previous section.
Using raw data in [74] , the magnetic parameter ![]() and angular momentum relations of the old star samples are shown in Figure 39, with triangle representing the measured values and the circles representing the theoretical equatorial magnetic fields, with no distinction between density ranges here.
and angular momentum relations of the old star samples are shown in Figure 39, with triangle representing the measured values and the circles representing the theoretical equatorial magnetic fields, with no distinction between density ranges here.
7.4. Explanation of the Magnetic Bode’s Law and the Law of Intrinsic Dipolar Field for Stellar Objects
We have provided names “young” & “old” for sun-like stars. The separation is not arbitrary. If we go through the data in Table 9(a) and Table 9(b), we will notice that most of the young stars have masses and radii satisfying roughly![]() . The reverse is true for old stars. In other words, we may roughly take a critical value of
. The reverse is true for old stars. In other words, we may roughly take a critical value of ![]() (i.e. the value
(i.e. the value![]() ) as an age boundary, which is gradual. The magnetic fields of the young ones are larger by almost an order of magnitude. Before we explain the magnetic Bode’s Law, let us put the measured surface fields for the young and old stars together in the
) as an age boundary, which is gradual. The magnetic fields of the young ones are larger by almost an order of magnitude. Before we explain the magnetic Bode’s Law, let us put the measured surface fields for the young and old stars together in the ![]() graph, covering a mass density range of several hundred to
graph, covering a mass density range of several hundred to ![]() (Figure 40). Triangles (darker ones are young, and the lighter blue ones are young) are data reported by measurement.
(Figure 40). Triangles (darker ones are young, and the lighter blue ones are young) are data reported by measurement.
Now let us recollect that we have derived an explicit expression for the equatorial field, represented by
![]() (7.1)
(7.1)
And the magnetic parameter is
![]() (7.2a)
(7.2a)
![]() (7.2b)
(7.2b)
![]()
Figure 39. The magnetic parameter ![]() vs angular momentum of the solid star model for sun-like stars with age between around 3 Gyr and 13 Gyr, as density ranging from several hundred to about 2.5 × 103 kg/m3.. Triangles are the measured data, and circles are equatorial dipolar fields predicted from the theory of Section (4) using raw data in [74] . The line of best fit for the measured points is roughly estimated to be between the lines pertaining to the equatorial and polar fields respectively.
vs angular momentum of the solid star model for sun-like stars with age between around 3 Gyr and 13 Gyr, as density ranging from several hundred to about 2.5 × 103 kg/m3.. Triangles are the measured data, and circles are equatorial dipolar fields predicted from the theory of Section (4) using raw data in [74] . The line of best fit for the measured points is roughly estimated to be between the lines pertaining to the equatorial and polar fields respectively.
where C1, C2 are constants. So our theoretical derivation tells us that if we plot ![]() against
against![]() , we should see a straight line with slope 0.75. The red & pink circles are points using the “raw data” from [74] , as listed in Table 9(a) and Table 9(b). The line of best does give a slope of 0.75 with perfect correlation. Many pink-red ones overlap. In fact, the red/pink circles represent the result of proving one is equal to one, because the linear relationship of the above two variables satisfy an equation which precisely state such relation. Note that Maxwell equation does not explicitly appear in our equation. According to the 5D projection theory, it is the structure of the spinors inside the void core that provides the origin (i.e. the electric current) of the magnetic field. Therefore, the mystery of the “hidden Maxwell equation” or the Magnetic Bode’s Relation/Law in astronomy can be explained by this model. We would remark also that such a law is satisfied by cool stars only-- precisely the condition of our Second Law of angular momentum [2] . The solid sphere model is very rough for a lump of plasma, as explained before. Therefore, we should expect there are some deviations in the slope of 0.75 in experimental findings.
, we should see a straight line with slope 0.75. The red & pink circles are points using the “raw data” from [74] , as listed in Table 9(a) and Table 9(b). The line of best does give a slope of 0.75 with perfect correlation. Many pink-red ones overlap. In fact, the red/pink circles represent the result of proving one is equal to one, because the linear relationship of the above two variables satisfy an equation which precisely state such relation. Note that Maxwell equation does not explicitly appear in our equation. According to the 5D projection theory, it is the structure of the spinors inside the void core that provides the origin (i.e. the electric current) of the magnetic field. Therefore, the mystery of the “hidden Maxwell equation” or the Magnetic Bode’s Relation/Law in astronomy can be explained by this model. We would remark also that such a law is satisfied by cool stars only-- precisely the condition of our Second Law of angular momentum [2] . The solid sphere model is very rough for a lump of plasma, as explained before. Therefore, we should expect there are some deviations in the slope of 0.75 in experimental findings.
Let us finally proceed to obtain demonstration of the Law of Intrinsic Dipolar Magnetic Field for Stellar Objects. When the equatorial field ![]() is plotted against
is plotted against![]() , the relation is strictly linear in the log-log plot, as demonstrated by the track of the pink circles for old stars in Figure 41. The power index is about 3.0 according to our theory. In other words, this general Law of Intrinsic Magnetic Dipole Field for stellar objects derived in this paper can simply be stated as
, the relation is strictly linear in the log-log plot, as demonstrated by the track of the pink circles for old stars in Figure 41. The power index is about 3.0 according to our theory. In other words, this general Law of Intrinsic Magnetic Dipole Field for stellar objects derived in this paper can simply be stated as
![]() (7.3)
(7.3)
For comparison, the measured surface magnetic fields published in [74] are plotted against ![]() also in the same figure, with blue triangles as data points.
also in the same figure, with blue triangles as data points.
We have shown only samples of one star group as an illustration. Other measured data points of the young stars behave in the same way. This law has been applied to analyze all the 8 star groups in Sections (6) & (7). We shall not repeat to show such similar graphs for other star groups. The reader can test this law readily. Such results show that once the “mechanical” data set (M, R, P) is obtained, the magnetic field can be calculated, without the explicit use of the Maxwell equations. This law is in line with the Law specified in Equation (7.2b) and the linear relation of ![]() studied in details in Section (6). Incidentally, there are 40 (circles) stars along the linear line in Figure 41, with lots of overlapping of star points. As in other graphs, the theoretical line goes through the midst of the experimental data; in this case,
studied in details in Section (6). Incidentally, there are 40 (circles) stars along the linear line in Figure 41, with lots of overlapping of star points. As in other graphs, the theoretical line goes through the midst of the experimental data; in this case, ![]() is deduced from theory and the range of
is deduced from theory and the range of ![]() for each star group is rather narrow. The upper limit of the vertical scale is 20 Gauss. The measured surface fields of the old sun-like stars fall into the range of a fraction of a Gauss to about ten Gauss.
for each star group is rather narrow. The upper limit of the vertical scale is 20 Gauss. The measured surface fields of the old sun-like stars fall into the range of a fraction of a Gauss to about ten Gauss.
7.5. On Dipolar Magnetic Fields of the Solar Planets and the Planets of the Trappist-1 System
There are some mysteries in the properties of the magnetic fields of our planets. Before we analyze them, let us list the relevant data/variables in Table 10 based on data from [75] [76] [77] . We plot the ![]() graph, treating them like stars. The densities of the 9 planets known have averaged densities ranging from
graph, treating them like stars. The densities of the 9 planets known have averaged densities ranging from ![]() (Saturn) to
(Saturn) to ![]() (Earth), not too wide a range, and we show the B-P relation (dark green circles) as one group in Figure 42. The power index is −0.871. The circle in the middle of the figure indicates the B-P data set of the Pluto-binary.
(Earth), not too wide a range, and we show the B-P relation (dark green circles) as one group in Figure 42. The power index is −0.871. The circle in the middle of the figure indicates the B-P data set of the Pluto-binary.
The reported measured equatorial fields of 7 planets are indicated by the orange triangles. According to rotation periods and their distances from the sun, it appears that five pairs appear-(i) Mercury (![]() , large;
, large;![]() ) & Venus
) & Venus![]() ; (ii) Earth
; (ii) Earth ![]() & Mars
& Mars![]() ; (iii) Jupiter
; (iii) Jupiter ![]() & Saturn
& Saturn![]() ; (iv) Uranus
; (iv) Uranus ![]() & Neptune
& Neptune ![]() ; (v) Pluto as a binary system
; (v) Pluto as a binary system ![]() .
.
In our model, the conformal projection of ![]() generates the SU (3) quarks. A proton is composed of a set of u, u, d quarks, due to gauge confinement. The bare total mass of these three quarks is
generates the SU (3) quarks. A proton is composed of a set of u, u, d quarks, due to gauge confinement. The bare total mass of these three quarks is![]() . Upon complete generation of electrons, we have a certain void radius
. Upon complete generation of electrons, we have a certain void radius![]() . We have derived, based on the uncertainty principle, when equal number of electrons and protons (i.e. hydrogen atoms) are generated, the size of the current loop in the 5D void is fixed:
. We have derived, based on the uncertainty principle, when equal number of electrons and protons (i.e. hydrogen atoms) are generated, the size of the current loop in the 5D void is fixed:![]() . The types and number of the quarks generated by P1 are determined by the principle of charge conservation and uni-direction nature of time. Since negative charges are generated by Po, only massive particles with positive or zero charges (forming hadrons), which satisfy gauge invariance in Lorentz space-time, can come to exist from this conformal projection P1. The lowest
. The types and number of the quarks generated by P1 are determined by the principle of charge conservation and uni-direction nature of time. Since negative charges are generated by Po, only massive particles with positive or zero charges (forming hadrons), which satisfy gauge invariance in Lorentz space-time, can come to exist from this conformal projection P1. The lowest
![]()
Figure 42. Theoretical equatorial magnetic fields of the 9 planets, treating them as stars, are indicated by the deep green circles. Taking into the consideration of the planets being appearing as 5 pairs and theoretically from Perelman entropy mapping as discussed in Section (7.5), B (eq, theory, G)/5 for the 9 planets are represented by the bright green circles―the B-P plot shows good correlation with a power index of −0.871. The reported measured fields are represented by orange triangles, and appear to be much closer to the bright green circles.
energy and thus rest mass of hadrons are the protons (composed of (u, u, d) quarks) and neutrons (composed of (u, d, d) quarks), meaning that the Lorentz mass shell contains only u and d quarks of charges (2/3)e, and -(1.3)e. To create a proton (u, u, d) and a neutron (u, d, d) from P1, it requires 2 e massless spinors states, but just 1-e massless spinor state. When all the possible electron-proton pairs are created, the system can only generate neutrons, or the sets of (u, d, d) quarks. The quark mass for neutron is![]() . Hence, the reduced quark mass for a (p, n) pair is
. Hence, the reduced quark mass for a (p, n) pair is![]() , and the loop radius
, and the loop radius ![]() increases by about 10%. As more matter is effectively “deposited” on the matter surface, R increases essentially, and there is a decrease of
increases by about 10%. As more matter is effectively “deposited” on the matter surface, R increases essentially, and there is a decrease of![]() . Thus, according to Equations (4.2.5) & (4.2.6),
. Thus, according to Equations (4.2.5) & (4.2.6), ![]() and it could decrease, despite there is increase of
and it could decrease, despite there is increase of![]() .
.
We plot the average surface temperature against distance from the sun in log- log scale (Figure 43), showing a straight line with power index of −0.593. If the planets were “materials” thrown out from the sun whose age is 4.6 Gyr, the heat energy of the planets would have been dissipated as thermal radiation, and the slope would be much steeper. We speculate that the solar system evolved from a Perelman entropy mapping. The angular momenta of the planets and the sun
![]()
Figure 43. Average surface temperature ![]() vs distance from the sun for the planets starting with mercury on the left, ending with Pluto on the right.
vs distance from the sun for the planets starting with mercury on the left, ending with Pluto on the right.
contribute to the total angular momentum of the Milky Way during the initial epoch. The rotation rate could have been deduced from the temperature if one were to observe these objects passed through a wide temperature range. Now these objects are already in the “cool range”, i.e. under the Second Law regime. Due to different processes of evolution and the fact that these stellar objects have very small masses as compared to the sun, the cooling process is very effective (so that the core temperature of the sun is >> than of the planets), and the mass density is in general much larger than that of the sun for the inner two pairs of planets.
In deriving the angular momentum of the e-trinos states in [2] , the normalized void radius ![]() is a function of T and even on cooling down to the Second Law region with
is a function of T and even on cooling down to the Second Law region with![]() , we have assumed that the temperature of the core is much greater than that on the surface, so that a large T gradient is established. Hence, the spinor state energy of the in-phase e-trinos depends on the core temperature and these spin states generate a certain amount of angular momentum. Such angular momentum is balanced by the angular momentum of the stellar object as we observe it. This balance is true for stars and most planets. However, the said T gradient is greatly reduced in Mercury and Venus because they are close to the solar surface, and their surface temperatures are high on receiving photons from the sun. Thus the spin state energies of the voids of Mercury and Venus are much lower than those of other planets. Moreover, there is coupling between the planet’s spin and its orbital angular momentum around the Sun. These two factors lead to the observed large P values of the Mercury and Venus (the same argument applies to the moon).If there were a planet existing almost on the solar surface, that planet would have practically zero spin (i.e.
, we have assumed that the temperature of the core is much greater than that on the surface, so that a large T gradient is established. Hence, the spinor state energy of the in-phase e-trinos depends on the core temperature and these spin states generate a certain amount of angular momentum. Such angular momentum is balanced by the angular momentum of the stellar object as we observe it. This balance is true for stars and most planets. However, the said T gradient is greatly reduced in Mercury and Venus because they are close to the solar surface, and their surface temperatures are high on receiving photons from the sun. Thus the spin state energies of the voids of Mercury and Venus are much lower than those of other planets. Moreover, there is coupling between the planet’s spin and its orbital angular momentum around the Sun. These two factors lead to the observed large P values of the Mercury and Venus (the same argument applies to the moon).If there were a planet existing almost on the solar surface, that planet would have practically zero spin (i.e.![]() ) and an observer on the Sun sees only one half of the surface.
) and an observer on the Sun sees only one half of the surface.
Thus, we consider that the generation of planets via the existence of the star sun is represented by the same group symmetry, and the 9 planets can be counted as 5 twins (with Pluto with its binary as a pair, but lying in the asteroid zone of the solar system). The arrangement of these planets shows Lie Group symmetry, due to SU(3) symmetry. There are two parity of choices in each element of the five (pairs) representation. In other words, there is a(p, n) duplet at the mass level, and the stellar object would split into two in view of, effectively, the SU(3) symmetry. Since the observed data suggests there are 5 pairs, similar to correct for spin multiplicity in a Fermi gas, the possible quantum states need to be divided by 5 when we do the averaging process for the loop current in calculating the dipole magnetic field. Thus we divide the dipole field strength by 5, and show the B-P graph in Figure 42 also (bright green circles). It is interesting to note that the measured values are then close to the theorized ones; the theoretical and measured values of the Earth overlap. Field of Mars is far off. We will provide an explanation of this abnormality below.
Let us first come back to the process of generation of mass in an individual planet, after splitting into pairs. Normally the ec current states of different energy E, and opposite charge and velocity signs, are statistically random, and therefore the parity bias in surface mass creation by P1, is not favored, but non-zero. If such abnormal distribution occurs, the equal number of states within each hemisphere can then be broken. Let us propose a simple scenario for P1 projection in Mars. Suppose the 2 e states came from Northern hemisphere, while the -e state, came from 1 loop in the Southern hemisphere. If that had happened, then the remaining e spinors in the north loop was less than the remaining -e spinors in the south. Such a repeated P1 projection, during Mars cooling (note that there are many volcanoes detected), will result in the magnetic field strength at the South Pole much greater than that at the North Pole [78] . For a similar reason but to a less degree in the stated parity bias property during the P1 projection, Venus could have a very weak magnetic field.
The dipolar planetary magnetic field shields the stellar particles radiation from impacting the planet’s surface without much energy lost; the magnetic field also serves to sustain the planetary atmosphere and to reduce possible material ejection from the planet’s surface. Thus Mars with an uneven dipole field and a thin atmosphere is known to have sent rocks that hit the earth.
In passing, we would remark that projection Po of the in-phase spinor states on the 3D surface of the void generate electrons in the Lorentz manifold, but leaving behind net positive massless spinor states on the void surface. A net current resulting from such states would generate magnetic field. Similarly, projection P1 of the out- of-phase spinor states in the 1D loops of the void generate quarks in the Lorentz manifold, but leaving behind net negative massless spinor states in the current loops of the void surface. Both events would lead to variation of the surface magnetic fields. Whether this model could explain the reversal of dipole polarity is outside the scope of this paper. We would also emphasize that most quarks and electrons were created when Perelman mappings were being implemented. The number of in-phase and anti-phase spinor states left over within the ![]() structure represents only a very small amount of the original number at the initial instant when there is infinite amount of energy in the universe.
structure represents only a very small amount of the original number at the initial instant when there is infinite amount of energy in the universe.
According to [79] , the basic data sets of the six planets nearest to the newly discovered Trappist-1 system are
![]()
![]()
![]()
![]()
![]()
![]()
where ![]() are respectively the mass and radius of the Earth. The equatorial dipole magnetic fields of these planets according to Equation (4.2.12) are respectively 0.925 Gauss; 0.974 Gauss; 0.43 Gauss; 0.33 Gauss; 0.216 Gauss; 0.255 Gauss, and the Trappist-1 star has a equatorial field of 59.8 Gauss. These planets have dipole fields of the same order of magnitude as that of Earth, while the star’s dipole field is many times that of the Sun. In our solar system, the solar wind, magnetic fields associated with sun’s spots are however much greater than the dipole field and causes deformation of the field line patterns creating the radiation belts in the magneto-spheres of the earth. As the planets in the Trappist-1 system are closer to their star than earth to the Sun, we need to know more about the sporadic fields, if any, from Trappist-1 before we can tell whether the dipole fields of these 6/7 planets can provide enough shielding from the star high energy particles radiation (for living organisms to survive). If oceans are present on these planets, at least deep water living organisms may have chance to survive even if the stated shielding is not strong enough, because the radiation energy released from this cool dwarf star is much weaker than that of the Sun. Thus knowledge of the magnetic fields is one decisive factor for us to consider in our search for living organisms there, and in what form. Before we get more information on such research, we show the B-P relation in Figure 44. Moreover, the magnetic parameter B-R3 is plotted vs angular momentum
are respectively the mass and radius of the Earth. The equatorial dipole magnetic fields of these planets according to Equation (4.2.12) are respectively 0.925 Gauss; 0.974 Gauss; 0.43 Gauss; 0.33 Gauss; 0.216 Gauss; 0.255 Gauss, and the Trappist-1 star has a equatorial field of 59.8 Gauss. These planets have dipole fields of the same order of magnitude as that of Earth, while the star’s dipole field is many times that of the Sun. In our solar system, the solar wind, magnetic fields associated with sun’s spots are however much greater than the dipole field and causes deformation of the field line patterns creating the radiation belts in the magneto-spheres of the earth. As the planets in the Trappist-1 system are closer to their star than earth to the Sun, we need to know more about the sporadic fields, if any, from Trappist-1 before we can tell whether the dipole fields of these 6/7 planets can provide enough shielding from the star high energy particles radiation (for living organisms to survive). If oceans are present on these planets, at least deep water living organisms may have chance to survive even if the stated shielding is not strong enough, because the radiation energy released from this cool dwarf star is much weaker than that of the Sun. Thus knowledge of the magnetic fields is one decisive factor for us to consider in our search for living organisms there, and in what form. Before we get more information on such research, we show the B-P relation in Figure 44. Moreover, the magnetic parameter B-R3 is plotted vs angular momentum ![]() in Figure 45. The good correlations indicate that these planets, like cool stars satisfy the linear B-P relation (log-log plot) and the Magnetic Bode’s law.
in Figure 45. The good correlations indicate that these planets, like cool stars satisfy the linear B-P relation (log-log plot) and the Magnetic Bode’s law.
7.6. Summary of the Discoveries Reported in This Paper
We have sketched the steps that during the mapping from 5D to 4D manifold, the 4th spatial variable in the 5D space-time structure would become the (non- zero) current loop with radius x’ at the 5D-4D boundary (one around each magnetic pole). In the unified 5D theories of Kaluza-Klein and Einstein, this space variable is compacted to zero, leading to gravitational singularity and hence black holes. Our deduction shows that such gravitational singularity does not exist, and the conclusion is well sup-
![]()
Figure 44. The theoretical equatorial dipole magnetic field of the six planets nearest to the newly discovered Trappist-1 system against the period of rotation![]() . The slope is ?0.764; values of the magnetic fields are stated in the text.
. The slope is ?0.764; values of the magnetic fields are stated in the text.
![]()
Figure 45. Change of ![]() with respect to variation of angular momentum is indicated, giving a power index of 0.86 for the 6 planets of the Trappist-1 system.
with respect to variation of angular momentum is indicated, giving a power index of 0.86 for the 6 planets of the Trappist-1 system.
ported by the numerous detections of stars with masses > 100 M⊙ (the largest one reported so far has a mass of![]() ) during the past two years.
) during the past two years.
Comparing the time intervals after the Big Bang when the lightest lepton (electron) is generated and that when the three quarks (building up a proton) join to form a proton, we obtain the radius of the loop current x’ in terms of the void radius Ro:
![]() (7.6.1)
(7.6.1)
for all stellar objects with hydrogen as fuel. The modification on x’ when the next heavier element (Helium) becomes the fuel of the star is also derived.
Analyzing the early stage of formation of a galaxy based on the 5D projection theory, we have provided an answer to the detection of unexpected gamma ray bubbles, one above, and one below a galaxy.
Since Maxwell equations are classical and valid in both the 5D and 4D manifolds, we have derived an explicit expression of the number density of the spinor pairs (which satisfies the Fermi-Dirac distribution but also form the current loop with radius x’ in the classical sense) at the 4D-5D boundary, with quantum signature based on (i) the uncertainty principle & (ii) quantum statistics. Viewed in a 4D Lorentz manifold, this current loop must produce a magnetic field in the classical sense. Therefore we simply apply the Biot-Savart law, with quantum nature incorporated in the number density of the e-trinos, to derive the expression of a distant magnetic field as observed on the matter surface of a stellar object. The surface magnetic field is found to be
![]() (7.6.2)
(7.6.2)
The variables are only M, R, P as the Fermi energy ![]() is taken to be the rest mass of electron because it is the lightest lepton generated, as explained in details in [2] and this paper. We call (7.6.2) as the Law of Intrinsic Dipole Magnetic Field (for stellar objects).
is taken to be the rest mass of electron because it is the lightest lepton generated, as explained in details in [2] and this paper. We call (7.6.2) as the Law of Intrinsic Dipole Magnetic Field (for stellar objects).
Expanding ![]() and
and ![]()
as convergent series, we discover that the approximate expression for B can be separated into three regions in temperature domain. In the high temperature domain where![]() ,
,
![]() (7.6.3)
(7.6.3)
We call Equation (7.6.3) the Law of Intrinsic Dipole Magnetic Field for Hot Stars. This law is applicable to fast rotating pulsars at very high temperature.
On the other hand, if![]() , Equation (7.6.2) becomes approximately
, Equation (7.6.2) becomes approximately
![]() (7.6.4)
(7.6.4)
Thus under the low temperature domain, B is independent of T. We call Equation (7.6.4) as the Law of Intrinsic Dipole Magnetic Field for Cool Stellar Objects. Such an interesting result is obvious because the angular momentum of the object is a function of the void radius Ro and the amount of current generated (hence the dipole field strength) near the magnetic poles in the 4D-5D boundary is also a function of Ro. The current density, which usually appears in Maxwell equations, is illuminated, giving the “un-ex- pected result” as specified in Equation (7.6.4). The transition temperature between the two domains is![]() , which is > the Bethe fusion temperature as discovered for angular momentum in [2] . We call such a temperature domain as the Law of Transition between Hot and Cool Stars.
, which is > the Bethe fusion temperature as discovered for angular momentum in [2] . We call such a temperature domain as the Law of Transition between Hot and Cool Stars.
Taking a cool star as a solid sphere as an approximation, it is elementary to show from Equation (7.6.4) that
![]() (7.6.5)
(7.6.5)
which is simply the “mysterious Magnetic Bode’s Law” found experimentally for cool stars.
We have found that for samples within a range of mass density, the ![]() plot is a straight line. Since for a star, P is inversely proportional to the rotation speed of the equator v, our analysis of nine star groups in Sections (6) & (7) explains why experimentally the relation between log (B) and log (v) (or log P) is found to be linear for many stars. Such a graph for all the star samples involved in this paper is presented in Figure 46.
plot is a straight line. Since for a star, P is inversely proportional to the rotation speed of the equator v, our analysis of nine star groups in Sections (6) & (7) explains why experimentally the relation between log (B) and log (v) (or log P) is found to be linear for many stars. Such a graph for all the star samples involved in this paper is presented in Figure 46.
Moreover, based on the numerical analysis in Sections (6) & (7) for nine star groups, we have found that once the power index of the ![]() for a number of samples is determined in graphing, we can write down explicit expression relating the variables (M, R, P) of this star group. We can use that expression to find out other crucial properties of that star group theoretically (such as M-R relation); such properties can be compared with experimental data directly. This (novel) method is useful to study stellar evolution, as experienced in our study on the young and old sun-like stars in Section (7.2) & (7.3).
for a number of samples is determined in graphing, we can write down explicit expression relating the variables (M, R, P) of this star group. We can use that expression to find out other crucial properties of that star group theoretically (such as M-R relation); such properties can be compared with experimental data directly. This (novel) method is useful to study stellar evolution, as experienced in our study on the young and old sun-like stars in Section (7.2) & (7.3).
We have proposed that electrons of the elements (atoms), starting with hydrogen could form 2D Semion states, with pinning of magnetic flux. Due to pressure wave or, in fact fluctuations during the natural cooling process, Semion state can be formed on/near the stellar surface when the gravitational force is
![]()
Figure 46. Predicted equatorial magnetic fields against period of rotation P for the following star groups: (1) Pre-main sequences stars of the Orion (light purple); (2) NGC 6819(orange); (3) Low-to Mid-Mass main sequence stars (bright red); (4) Sun-like young stars (red slightly deeper than that of group (3)) & sun-like old stars (deep red). Notice that the young ones are close to groups (2) & (3), whereas the old ones are close group (1) instead.(5) Pre-dwarfs M34 (bright green); (6) NGC 2516 (pink); (7) Brown Dwarfs (brown); (8) White Dwarfs (blue); (9) Magnetic White Dwarfs (light bright blue). Note that the line of best fit is drawn through each group except the sun-like group (4). Since each group covers a relatively wide mass density, the slopes of the 8 lines above are slightly different from the values analyzed in Section (6). Many points of stars are overlapping. As data for some stars are averaged over a much larger number of stars, the total effective number of stars analyzed is well over 2000. Power indices and correlation coefficients have already been specified in the analysis of each star group.
very large and the void radius ![]() is relatively small. The Semion quasi-particles could get back to the 3D states due to fluctuation in thermo dynamical balance, releasing huge magnetic field, such as that observed in slowly rotating, high density White Dwarfs. Thus, we have provided a plausible explanation for the emergence of huge magnetic field in many stars, including very old ones.
is relatively small. The Semion quasi-particles could get back to the 3D states due to fluctuation in thermo dynamical balance, releasing huge magnetic field, such as that observed in slowly rotating, high density White Dwarfs. Thus, we have provided a plausible explanation for the emergence of huge magnetic field in many stars, including very old ones.
We have provided an explanation of the asymmetry of magnetic field on the Martian surface and compared the measured and theoretically deduced dipolar magnetic fields of the planets. For the different star groups we studied in Section (6), we cannot compare directly the theoretical magnetic field values with all the stars because we it is difficult to find the published complete set of data for most of these stars. Group comparison (such as Brown Dwarfs group) indicates that our predicted results are in line, in fact, within the same order of magnitude, with observational data and in general trends. For the sun-like group where the whole set of data (B, M, R, P) are available, theoretical predicted values agrees quite well with data (within an order of magnitude), considering the uncertainty and limitation in measurements discussed in details in Section (7.1).
We predict the equatorial fields B of the newly discovered Trappist-1 star and the 6 nearest planets. The B − P graph, and the B R3 ? Iω graph in the log-log plots for the 6 planets are both linear.
7.7. Conclusion
Based on the homogeneous 5D model of the universe, we have developed explicit expressions to explain quite a number of unanswered queries or mysteries in astrophysics, as outlined in Section (7.6). One step further, we hope that similar study can serve someway in building a part of the bridge to embrace Maxwell electro-magnetism and quantum mechanics in the future.
Acknowledgements
We wish to express our gratitude to the various types of assistance of Mr. Benjamin Fung and Dr. Junling Gao, Mr. Vincent Wan during the preparation of this manuscript. We appreciate Mr. Cressidy Fan for plotting Figure 1. We would also wish to express our thanks to Dr. Gisela Dreschhoff, and Dr. Hogne Jungner for their critically reading of the manuscript, plus Dr. Wilson Wong for discussion on issues related to this paper. Last but not least, we thank Professor W. K. Chow for his help when in need for this long project. Both authors declare that there is no conflict of interests in this academic project.
Appendix A: Explicit Expression of the Void Radius
To calculate the void radius![]() , we need to review a few steps of angular momentum of the in-phase spinor pairs inside the void
, we need to review a few steps of angular momentum of the in-phase spinor pairs inside the void
![]() (A.1)
(A.1)
where![]() ,
, ![]() is the spin degeneracy, p the momentum,
is the spin degeneracy, p the momentum, ![]() is the Fermi-Dirac distribution and the other symbols are standard polar coordinate variables.
is the Fermi-Dirac distribution and the other symbols are standard polar coordinate variables.
If we treat s pair of in-phase spinors of opposite charge as a bound state, the energy is taken to be the additive energy in the pair. We have already noted in [6] that e,-e are two different types of Fermi particles, and the total angular momentum is then twice of that pertains to either one type―the above expression is then multiplied by a factor of two. The resulting total angular momentum deduced from these two types of treatment different by a numerical constant of several times only. For astronomical estimation, we have considered the loop current based on the Biot-Savart Law to be the additive sum of two currents due to oppositely rotating spinor charges in section (4). Here we also take that the total angular momentum of the system to be twice that in the above equation. Integrating over![]() , with the spin degeneracy to be 4, the total angular momentum
, with the spin degeneracy to be 4, the total angular momentum
![]() (A.2)
(A.2)
![]()
The constant D is found to be:
![]() (A.3)
(A.3)
Under the region satisfied by the Second Law of Angular Momentum, it has been shown in [2] that
![]() approximately. (A.4)
approximately. (A.4)
Considering a stellar object to be a solid sphere with mass M, radius R, period of rotation P, conservation of angular momentum among the 5D void and the 4D matter shell requires that
![]()
Giving
![]() (A.5)
(A.5)
Numerically,
![]() .
.
![]()
The dimension of![]() , thus the dimension of R.H.S. of (A.5) is m. Therefore,
, thus the dimension of R.H.S. of (A.5) is m. Therefore,
![]() (A.6)
(A.6)
Appendix B: Converging Series of the Integral ![]()
![]() (B1)
(B1)
where
![]() (B.2)
(B.2)
![]() (B.3)
(B.3)
With![]() , and
, and ![]() , k = Boltzmann constant and T is the temperature. In
, k = Boltzmann constant and T is the temperature. In![]() , the Fermi-Dirac distribution function
, the Fermi-Dirac distribution function
![]()
is bounded for a wide range of ![]() in our study, and F varies between ⋍ 1/2 and 1.0. We can therefore expand
in our study, and F varies between ⋍ 1/2 and 1.0. We can therefore expand ![]() as a series:
as a series:
![]() (B.4)
(B.4)
Now ![]() (B.5)
(B.5)
Integration by parts gives,
![]() (B.6)
(B.6)
![]() (B.7)
(B.7)
![]() (B.8)
(B.8)
![]() (B.9)
(B.9)
![]() (B.10)
(B.10)
![]() (B.11)
(B.11)
Summing all the series, we arrive at
![]() (B.12)
(B.12)
Transforming![]() , Equation (B.3) becomes the sum of two definite integrals with explicit forms:
, Equation (B.3) becomes the sum of two definite integrals with explicit forms:
![]() (B.13)
(B.13)
From (B.1), (B.12),(B.13),
![]() (B.14)
(B.14)
When![]() , the two converging series cancel, and
, the two converging series cancel, and
![]() (B.15)
(B.15)
When![]() ,
,
![]() (B.16)
(B.16)
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org