1. Introduction
Developing a quantum model of gravity has been an important conceptual goal in physics [1] - [6] . Uniting cosmologic physics and quantum physics is a continuing incomplete process. Many different models have been proposed, but none have seamlessly united quantum, classical and cosmologic phenomena [7] . Neutron, n0, neutron stars, NS, and black holes, BH, are ideal conceptual, computational, and observational settings to interrogate gravitational properties at the extremes of short and long distances, and high gravitational binding energies, GBEs [8] - [14] . Many new observations are being acquired that lend themselves to interpretations of the basic properties and scaling of gravitational systems. Recent gravity wave measurements are dependent upon a robust gravity model [15] [16] .
A NS is related to the transformation of atomic matter, in the simplest case hydrogen, H, to a degenerate n0 state driven by gravity. NSs can be characterized by a few physical factors since they are composed predominately of neutrons, and these are referred to as equations of state [17] [18] . Some theoretical studies consider NSs as pure n0 matter [19] . Some models describe the core as superfluid neutron-degenerate matter (mostly neutrons, with some protons and electrons). About 5% of all known NSs are in binary systems [20] . In some theories of binary evolution it is expected that NSs also exist in binary systems with a BH. It has been proposed that coalescence of binaries consisting of two NSs may be responsible for producing short gamma-ray bursts [21] .
A BH is a mathematically defined region of spacetime exhibiting such a powerful gravitational force that no particle or electromagnetic radiation can escape. The classic Schwarzschild radius equation states that a BH arises when the annihilation energy of the total mass with a Schwarzschild radius of rs, (massBH_rs)c2 in joules, equals two times GBE in joules for any BH horizon measuring rs (see Equation (1) and Equation (2)). From a quantum perspective of a pure binary NS system transformation to a BH, Equation (2) is a mathematical imperative expressing the equivalence between the integer number of neutrons defining the annihilation mass and the paired masses defining the GBE [22] [23] .
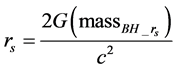 (1a)
(1a)
or
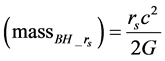 (1b)
(1b)
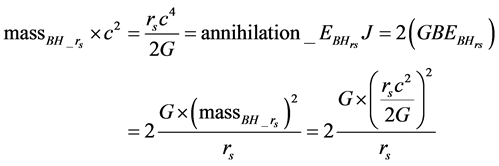 (2)
(2)
This is a specialized physical/mathematical setting where two entities, annihilation energy of a mass and a different form of energy, two times of the binding energy in this case, must be identically scaled in a paired relationship. It leads to a dimensionless quantum number of neutrons relationship defining both simultaneously. Another similar physical single and paired example would be related to matter/anti-matter pair production which is also important in the properties of BHs [24] . In pair product there are photon and two anti-particles in which the total energies are scaled equally. In anti-matter matter annihilation there are two matter entities and two photons. The number 2 reflects the paired physical state relationship. Both are associated with physical transformation settings where the velocity of matter is related to the speed of light, c, and the annihilation energy of the rest mass, mc2. In the transformation of a binary system of NSs to a BH, the GBE scaling can be defined equivalently and solely in integer multiples of the energy of n0, equaling 1.5053 × 10−10 J, which is a natural energy unit. This energy unit could be also expressed in term of its equivalent in frequency, 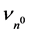 , (by dividing the energy by Planck’s constant h) or in terms of n0 Compton wavelength,
, (by dividing the energy by Planck’s constant h) or in terms of n0 Compton wavelength, . Therefore gravity can be scaled as a single natural unit system that is inter-related by integer multiples or integer fractions of n0 units.
. Therefore gravity can be scaled as a single natural unit system that is inter-related by integer multiples or integer fractions of n0 units.
The goal of this paper is to evaluate the specific units from a quantum integer perspective of a natural scaling based solely on the neutron, which define a system of gravity that is conceptually and computationally consistent with standard gravitation models and methods for NSs and BHs.
2. Virtual Neutron Gravity Energy Unit, GBEn0_unit
We define the simplest virtual n0 based natural unit gravitational system, GBEn0_unit, as the GBE of virtual paired n0 masses separated by , a distance that is equal to the speed of light divided by the annihilation frequency of the neutron,
, a distance that is equal to the speed of light divided by the annihilation frequency of the neutron,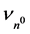 . The GBE in Joules of this system, GBE n0_unit J, 1.4188 × 10−49 J, is described in Equation (3).
. The GBE in Joules of this system, GBE n0_unit J, 1.4188 × 10−49 J, is described in Equation (3).
 (3)
(3)
Here, 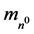 denotes the mass of the neutron, 1.6749 × 10−27 kg, G, the universal Newtonian gravitational constant, and c the speed of light. vn0 represents the frequency equivalent of the neutron, 2.2719 × 1023 Hz,
denotes the mass of the neutron, 1.6749 × 10−27 kg, G, the universal Newtonian gravitational constant, and c the speed of light. vn0 represents the frequency equivalent of the neutron, 2.2719 × 1023 Hz,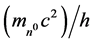 .
. 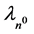 is the n0 Compton wavelength 1.3196 × 10−15 m.
is the n0 Compton wavelength 1.3196 × 10−15 m. 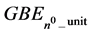 values in other physical unit equivalents include frequency 2.1413 × 10−16 Hz (
values in other physical unit equivalents include frequency 2.1413 × 10−16 Hz (![]() ), Compton wavelength 1.4001 × 1024 m, and mass 1.5787 × 10−66 kg.
), Compton wavelength 1.4001 × 1024 m, and mass 1.5787 × 10−66 kg.
3. Virtual Neutron Gravity Dimensionless Coupling Proportionality Constant Unit, kn0_unit
GBEn0_unit J is related to a proposed dimensionless coupling proportionality constant ratio with the n0_unit in J, with ![]() equaling 9.4252 × 10−40 from Equation (4) in multiple physical units. Here n0 J represents the Joule equivalent of n0, 1.5053 × 10−10 J. This proportionality constant is referred to as
equaling 9.4252 × 10−40 from Equation (4) in multiple physical units. Here n0 J represents the Joule equivalent of n0, 1.5053 × 10−10 J. This proportionality constant is referred to as![]() , where
, where ![]() times any physical unit value of the neutron equals
times any physical unit value of the neutron equals ![]() in the corresponding unit.
in the corresponding unit.
![]() (4)
(4)
4. kn0_unit, Planck Time, and Hydrogen
Our proportionality constant, kn0_unit is also defined by several equivalent relationships involving GBEn0_unit; Planck’s constant, h; Planck time, tP; and the frequency equivalents of the neutron, proton (p+), electron (e−), Bohr radius (a0), and GBE of the electron in hydrogen; respectively vn0, vp+, ve−, ![]() , vGBE_e in Equation (5). The vGBE_e is derived and valid identical to the Bohr radius derivation. These are also natural unit constants. One is defined by the degenerate neutron state and the other equivalently by the hydrogen state that is non-degenerate. Additionally, the negative n0 beta decay products represent the closest natural gravitational system to the virtual pure n0 system. Thus we find that the n0 serves as a fundamental unit for the origin of all of the hydrogen products as well. The product of
, vGBE_e in Equation (5). The vGBE_e is derived and valid identical to the Bohr radius derivation. These are also natural unit constants. One is defined by the degenerate neutron state and the other equivalently by the hydrogen state that is non-degenerate. Additionally, the negative n0 beta decay products represent the closest natural gravitational system to the virtual pure n0 system. Thus we find that the n0 serves as a fundamental unit for the origin of all of the hydrogen products as well. The product of![]() , the frequency of one mass, the frequency of the other mass, the frequency of the distance equals the GBE in Hz. In the neutron unit setting the kn0_unit is related to the product of
, the frequency of one mass, the frequency of the other mass, the frequency of the distance equals the GBE in Hz. In the neutron unit setting the kn0_unit is related to the product of ![]() and
and![]() , divided by vn0, therefore the product of
, divided by vn0, therefore the product of ![]() and
and![]() , Equation (5).
, Equation (5).
![]() (5)
(5)
From Equation (5) the ratio of vGBE_n0_unit divided by vGBE_e− is related to the ratio of quantum entities of ![]() cubed divided by the product of vp+, ve−, and
cubed divided by the product of vp+, ve−, and![]() , 7.3836 × 107, Equation (6).
, 7.3836 × 107, Equation (6).
![]() (6)
(6)
5. Proposal of a Gravitational Constant Analogous of the Fine Structure Constant, αG
We also find interest in computing the square root of![]() , 4.3417 × 10−20, a dimensionless constant similar to the fine structure constant, α, in both concept and computation, but for gravitational, non-electromagnetic physical systems. It is described herein as αG, Equation (7). The fine structure constant α is related to the electromagnetic binding energy of the electron in H, and involves p+, e−, and a0. Additionally αG represents the ratio of a velocity divided by c that is also a β value from Special Relativity. This is described as βG for this specific setting, just as α represents a specific β for hydrogen. The mass of the electron times the product of
, 4.3417 × 10−20, a dimensionless constant similar to the fine structure constant, α, in both concept and computation, but for gravitational, non-electromagnetic physical systems. It is described herein as αG, Equation (7). The fine structure constant α is related to the electromagnetic binding energy of the electron in H, and involves p+, e−, and a0. Additionally αG represents the ratio of a velocity divided by c that is also a β value from Special Relativity. This is described as βG for this specific setting, just as α represents a specific β for hydrogen. The mass of the electron times the product of ![]() squared divided by two is equal to the ionization binding energy of hydrogen, which is the Rydberg constant equivalent. The kinetic energy and the binding energy are similar in concept to the transformation point to a BH in Equation (2). An identical gravitational mathematical property will be shown later in Equation (8).
squared divided by two is equal to the ionization binding energy of hydrogen, which is the Rydberg constant equivalent. The kinetic energy and the binding energy are similar in concept to the transformation point to a BH in Equation (2). An identical gravitational mathematical property will be shown later in Equation (8).
![]() (7)
(7)
The kinetic energy of this virtual n0-system is the mass of n0 times the product of (αG × c) squared divided by 2. This equals![]() , Equation (8). Thus we find the Gravitational Binding energy neutron unit exactly equals the kinetic energy of the binary neutron pair identical to the pattern seen with one definition of α. This pure n0-based unit gravitational system is a virtual system because it does not have a significantly long lifetime. Our derived constant αG equals the square root of the product of 2 and
, Equation (8). Thus we find the Gravitational Binding energy neutron unit exactly equals the kinetic energy of the binary neutron pair identical to the pattern seen with one definition of α. This pure n0-based unit gravitational system is a virtual system because it does not have a significantly long lifetime. Our derived constant αG equals the square root of the product of 2 and ![]() squared times the frequency equivalent of the GBE of the electron in hydrogen, vGBE_e− divided by the product of vp+, ve−, and
squared times the frequency equivalent of the GBE of the electron in hydrogen, vGBE_e− divided by the product of vp+, ve−, and ![]() from Equation (7). This unites gravitational scaling and multiple other fundamental quantum entities.
from Equation (7). This unites gravitational scaling and multiple other fundamental quantum entities.
![]() (8)
(8)
The mathematical connection with the closest natural atomic system, which represents hydrogen, shows that vGBE_e is a fundamental constant with similar importance to quantum gravity, and is analogous to the significance of the electromagnetic binding energy of the electron in H to photon and electromagnetic systems. This constant cannot be measured, but it does not diminish its physical significant. In fact, the Bohr radius, rest mass of the electron, and the Rydberg constant that define the hydrogen quanta cannot be experimentally measured either. This fundamental frequency vGBE_e− equals, 2.9000 × 10−24 Hz; equivalently 2.1381 × 10−74 kg; 1.0337 × 1032 m; or 1.9216 × 10−57 J. The product of ![]() and vGBE_e− equals 0.65885 Hz2 so vGBE_e− is closely scaled by the mathematical scalar reciprocal of
and vGBE_e− equals 0.65885 Hz2 so vGBE_e− is closely scaled by the mathematical scalar reciprocal of![]() . Whence vGBE_e− divided by the product of vp+, ve−, and
. Whence vGBE_e− divided by the product of vp+, ve−, and ![]() also equals the fundamental gravitational, quantum, and relativistic constant Planck time squared,
also equals the fundamental gravitational, quantum, and relativistic constant Planck time squared,![]() . Planck time
. Planck time ![]() (h not the reduced Planck’s constant, ħ) equals 1.35141(08) × 10−43 s. All frequency equivalent gravitational systems fulfill the relationship of the
(h not the reduced Planck’s constant, ħ) equals 1.35141(08) × 10−43 s. All frequency equivalent gravitational systems fulfill the relationship of the ![]() ratio including that of hydrogen and vGBE_n0_unit, Equation (7).
ratio including that of hydrogen and vGBE_n0_unit, Equation (7).
The value of αG equals the product of square root of 2, ![]() , and tP as derived in Equation (7). Thus αG is inter-related with the quantum gravitational property of H in an analogous fashion as α is inter-related to both the quantum and electromagnetic properties of H. Now GBEn0_unit can be calculated from ratio/product relationships of
, and tP as derived in Equation (7). Thus αG is inter-related with the quantum gravitational property of H in an analogous fashion as α is inter-related to both the quantum and electromagnetic properties of H. Now GBEn0_unit can be calculated from ratio/product relationships of ![]() as seen in Equation (8).
as seen in Equation (8).
6. Definition of the Newtonian Gravitation Constant in Neutron Units
As an added and quite surprising result the Newtonian gravitational constant G can be completely defined in the defined units of the n0 mass, its Compton wavelength, its unit GBE; or with c and neutron frequency equivalent as in Equation (9).
![]() (9)
(9)
Equivalently, the Newtonian gravitational constant G can also be defined in units of n0, c, h, tP, vp+, ve−, va0, vGBE_e−,and neutron beta decay products in H as shown in Equation (10). This is analogous to the inter-relationship of multiple fundamental quantum constants that can define a0 or α.
![]() (10)
(10)
7. Gravitational Binding Energy of Any System from an Integer Neutron Perspective
The GBE can be calculated for any system using the integer unit n0 perspective by Equation (11). ![]() is the integer number of equivalent neutrons of one mass, #1n0. Also
is the integer number of equivalent neutrons of one mass, #1n0. Also ![]() equals the integer number of neutron equivalences of the second mass, #2n0. We define #λn0 as the integer number of n0 Compton wavelengths of the masses separation distance, λ. All of the # values are dimensionless integers.
equals the integer number of neutron equivalences of the second mass, #2n0. We define #λn0 as the integer number of n0 Compton wavelengths of the masses separation distance, λ. All of the # values are dimensionless integers.
![]() (11)
(11)
8. An Example of the Transition of a Symmetric Binary Pure Neutron NS System to a BH
Consequently we have just established the transformation of binary symmetric NSs of identical mass, merging into a BH as in Figure 1. rs is arbitrarily chosen to be c × s for mathematical simplicity, and it is a fundamental unit distance linked to all of the other constants. A Schwarzschild radius, rs, of c × s equals 299,792,458 m is utilized to demonstrate a relevant cosmological dimension in the Schwarzschild ratios shown in Equation (12). The mass of such a BH equals the product of c2 times c × s divided by the product of 2 times the gravitational
![]()
Figure 1. Transformation of a symmetric binary neutron star system to a black hole. Figure 1 is a plot showing the transformation of the binary symmetric neutron system to a black hole with a Schwarzschild radius of c × s. The X-axis is log10 # of n0. The Y-axis is in log10 Joules of the annihilation energy of the # of n0, the upper blue line; and 2 times the gravitational binding energy, GBE, of a system with # of n0 separated at a distance of c × s, the lower green line, Equation (2). The far left side of the plot begins at a binary single n0 system. To the right the integer number of n0 of each component of the pair increases towards 1.2051 × 1062 neutrons. At that specific # of n0, red circle, 2 times the GBE and the annihilation energy of the mass are equal leading to the transformation to a BH.
constant G, which computes to a total mass of 2.0186 × 1035 kg from Equation (12). This is described as![]() . Other unit equivalents of
. Other unit equivalents of ![]() are: 1.8141 × 1052 J; frequency of 2.7379 × 1085 Hz; Compton wavelength of 1.0950 × 10−77 m; and integer number of neutrons 1.2051 × 1062n0. We evaluate the GBE of a paired neutron system starting with 1 n0 to 1.2051 × 1062 n0, or 2.0186 × 1035 kg for the mass. The product of 2, the mass squared and G divided by c × s equals twice the GBE of each individual incremental pair neutron systems, Equation (13).
are: 1.8141 × 1052 J; frequency of 2.7379 × 1085 Hz; Compton wavelength of 1.0950 × 10−77 m; and integer number of neutrons 1.2051 × 1062n0. We evaluate the GBE of a paired neutron system starting with 1 n0 to 1.2051 × 1062 n0, or 2.0186 × 1035 kg for the mass. The product of 2, the mass squared and G divided by c × s equals twice the GBE of each individual incremental pair neutron systems, Equation (13).
![]() (12)
(12)
![]() (13)
(13)
The factor 2 is taken into account in these calculations to define the point of transition of the binary n0 masses to a BH. Since the GBE increases with the square of the number of n0 there is a point where the two lines and energy values converge, Figure 1. This is the transformation point to a BH. At neutron star pairing with a mass of 2.0185 × 1035 kg 2 times the GBE equals the annihilation energy of the mass fulfilling the mathematical definition of a BH, Equations ((2), (13)). This demonstrates that binary gravitational systems from any pairing of two neutrons, two stars, and two NS, and one BH can be described by a quantum n0-based system.
9. Discussion
These results show how gravitation systems, indeed the Newtonian Gravitational constant itself, can be completely scaled by a quantum or n0-unit system (see Equations ((9)-(11)).) This is an imperative of the mathematical definitions of pure NSs transforming to simplest non-rotating BHs. The GBE of any system represents dimensionless integer fractional values of the neutron as the base unit, which provides dimensionless ratio coupling constants defined by kn0_unit and αG. Surprisingly, these are related to quantum subatomic constants derived from the frequency equivalents of the neutron, hydrogen, and tP, (Equation (10)). This demonstrates a system that bridges from quantum to gravitational. Similarly both α and αG represent conceptually and computational parallel β values, but are relegated to widely divergent physical settings. The fine structure constant α relates to electromagnetic relationships of hydrogen, whereas αG is for neutron gravitational relationships. The electromagnetic binding energy of the electron in hydrogen, related to the Rydberg constant, is a fundamental scaling factor for all electromagnetic relationships including α. The GBE of the electron in hydrogen plays an identical role for neutron quantum gravity. Though our derived GBE_e-value is not directly observable it still represents an important fundamental inter-relational constant identical in concept to the other hydrogen quanta.
The time and distance units of gravity may also be defined by n0-equivalents. The time unit is one second divided by![]() , 4.4017 × 10−24 s. The distance unit is λn0,
, 4.4017 × 10−24 s. The distance unit is λn0, ![]() equals 1.3196 × 10−15 m. Any gravitational system can be interrogated where time, distance, matter, and energy can all be evaluated as one of these quantum states. Likewise in quantum physics, where there are only specific quantum states possible, the only possible gravitational states are related to integral numbers of neutrons for the masses and
equals 1.3196 × 10−15 m. Any gravitational system can be interrogated where time, distance, matter, and energy can all be evaluated as one of these quantum states. Likewise in quantum physics, where there are only specific quantum states possible, the only possible gravitational states are related to integral numbers of neutrons for the masses and ![]() for the distances in a purely n0-unit gravitational system, Equation (11). Clearly, all possible GBEs are also only integer or integer fraction values of
for the distances in a purely n0-unit gravitational system, Equation (11). Clearly, all possible GBEs are also only integer or integer fraction values of![]() . Perhaps the quantization of the gravitational field may be discovered in our approach.
. Perhaps the quantization of the gravitational field may be discovered in our approach.
10. Conclusions
In conclusion, mathematical definitions of pure Neutron Stars and Black Holes define an imperative that the scaling of the gravitational binding energy must be defined in quantum unit equivalents of the neutron. The dimensionless ratios, kn0_unit and αG, of a pure neutron gravitational system, are defined by four quantum entities, and the n0, the speed of light, the products of negative n0 beta decay, p+, e−, a0, vGBE_e−, as in Equations ((5), (7)). Newton’s Gravitational constant G, can be defined solely in n0-units and/or the speed of light, tP, and hydrogen quantum values as in Equations ((9), (10)). Therefore gravity can be viewed as being scaled by the neutron which is an imperative in the NS BH transition. Time (chronon), matter (second quantization), distance (Planck scales), and energy (Rydberg spacing) also must be quantum integer based on n0. Since all of the dimensions of a gravitational system are scaled by a single natural unit, the neutron, the system can be computationally analyzed as dimensionless inter-re- lationships just as electromagnetic systems are with the fine structure constant as in Equation (11).
Acknowledgements
We would like to thank Richard Vento, Columbus State Community College― retired for his help in the preparation of the paper.