The Barrier Properties of Flake-Filled Composites with Precise Control of Flake Orientation ()
1. Introduction
Additive manufacturing, especially in the form of 3D printing, offers the exciting possibility of generating articles with precisely controlled internal microstructure. One area in which this feature can be of significant advantage is in diffusion control, specifically in the design and fabrication of microstructures which allow for minimization of the transport of a solute to/from a contained fluid. Flake-filled polymeric composites, incorporating mica, glass or metallic flakes have found many uses in this direction, as they offer significant processing and property advantages, namely high dimensional stability and low warpage in molding, uniform in-plane mechanical properties, corrosion protection, sound insulation as well as appearance and color control [3] [4] [5] [6] [7] . Micron-sized flakes of inorganic materials such as mica, nano-scale platelets of clay minerals such as hectrite, saponite and montmorillonite and more recently graphene-oxide platelets of aspect ratios well over 1000, have been used for this purpose [8] . It has been demonstrated that incorporation of such fillers aligned perpendicular to the direction of macroscopic diffusion can be very effective in increasing the tortuosity of the diffusion path of the diffusing species. When the flakes are randomly placed, as would be the case in a flake composite manufactured from the melt, the predicted improvement in barrier efficiency ranges from being ~( ) in dilute systems, where (
) in dilute systems, where ( ) is the aspect ratio and (
) is the aspect ratio and ( ) the volume fraction of the flakes, to being ~
) the volume fraction of the flakes, to being ~ in more concentrated dispersions [1] [9] - [16] .
in more concentrated dispersions [1] [9] - [16] .
One notable disadvantage of traditional processing methods vis-à-vis flake- filled composites is the fact that flake orientation cannot be precisely controlled. In such operations (extrusion, compression or injection molding, thermoforming and others) flake orientation is achieved due to the propensity of the flakes to orient in accordance to the prevailing flow field―either in the main direction of flow when the flow is shear or transverse to it when the flow is extensional [17] . An additional shortcoming of traditional flow-processing routes is the inability to utilize high flake loadings since, in that case, the viscosity of the resulting melt becomes prohibitively high. Given the capability afforded by 3D printing to fully control flake orientation as well as generate articles with flake loadings approaching those at maximum packing, it is desirable to predict the effective diffusion coefficient (or its inverse, the barrier improvement factor, BIF) as an explicit function of the flake orientation angle and for very high, previously untenable, concentrations.
The two main approaches which have been used in the literature to-date for this purpose are (i) an ad-hoc incorporation of orientation metrics in existing models for the BIF [8] [18] and (ii) derivation of BIF models from diffusion path calculations [19] [20] [21] . In both cases, the proposed models have been derived for low or very-low flake concentrations and have not been extensively tested in the moderate to high-concentration regime, which will be of importance in any 3D printing application. In addition, by not respecting the rotational properties of the diffusivity tensor, these models are not grounded on a sound theoretical footing. This paper addresses the above issues both computationally and theoretically, by proposing a model based on the two principal diffusivities of a flake composite. We also show that the implications of our theoretical model are fully supported by extensive computational results.
2. Computational
We carry out steady-state diffusion computations in doubly-periodic unit cells containing up to 3000 individual flake cross-sections. These are added in the domain sequentially, using a Random Sequential Addition (RSA) procedure. Specifically, at each flake placement attempt, two random numbers are used to assign the coordinates of the flake center while its orientation angle (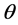 ) is fixed and the same for all flakes. If, after placement, no overlap with other flakes is detected, the process continues with the next flake, until the desired number of flakes has been placed, or, until no flake can be placed after 50,000 attempts; in this case no geometry is generated. In order to enable subsequent meshing of the computational domain, a minimum allowable distance between flakes is imposed; this is (
) is fixed and the same for all flakes. If, after placement, no overlap with other flakes is detected, the process continues with the next flake, until the desired number of flakes has been placed, or, until no flake can be placed after 50,000 attempts; in this case no geometry is generated. In order to enable subsequent meshing of the computational domain, a minimum allowable distance between flakes is imposed; this is (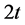 ) where (
) where (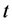 ) is the thickness of the flake. Since in this work we have dealt with flakes of high aspect ratio (
) is the thickness of the flake. Since in this work we have dealt with flakes of high aspect ratio (![]() and
and![]() ), this minimum distance requirement is deemed reasonable so as to not result in excessive local mesh refinement. In a rectangular unit cell of dimensions (H) and (L) containing (N) flakes of dimensions (
), this minimum distance requirement is deemed reasonable so as to not result in excessive local mesh refinement. In a rectangular unit cell of dimensions (H) and (L) containing (N) flakes of dimensions (![]() ), the flake area fraction (
), the flake area fraction (![]() ) is
) is ![]() and the length (l) of each flake
and the length (l) of each flake![]() . We have looked at systems in which
. We have looked at systems in which![]() . At higher values of (
. At higher values of (![]() ) it becomes impossible to fill the space with non-overlapping flake crossections. This not-withstanding, the present study is to our knowledge the first to investigate systems of such large concentration.
) it becomes impossible to fill the space with non-overlapping flake crossections. This not-withstanding, the present study is to our knowledge the first to investigate systems of such large concentration.
In multi-particle simulations, use of doubly-periodic cells is essential when dealing with elongated particles so as to eliminate artifacts of oriented (or, depleted) layers which would otherwise appear adjacent to cell boundaries [11] [16] . The effect of the RVE dimensions on the computed effective diffusivity is also eliminated when using periodic unit cells. A sample unit cell, showing flakes oriented at an angle θ = 0.8 rad with respect to the horizontal (x) axis (extended slightly outside the limits of the unit cell to show the doubly-periodic geometry) is shown in Figure 1.
The boundary conditions are cyclic on the right and left boundaries, namely![]() . On the top and bottom boundaries, fixed values of concentration are prescribed. On the surface of each flake we impose
. On the top and bottom boundaries, fixed values of concentration are prescribed. On the surface of each flake we impose ![]() indicating that the flakes are impermeable. At each level of (
indicating that the flakes are impermeable. At each level of (![]() ) and (
) and (![]() ) we generate ~10 different realizations, each containing up to 3000 randomly
) we generate ~10 different realizations, each containing up to 3000 randomly
placed flakes. The computational meshes are created by the mesh generating program Salome through an in-house automated procedure and contain ~106 triangular elements.
These meshes are then used by Open Foam to solve the steady-state diffusion equation![]() , (C) being the solute concentration, and provide its distribution in the domain of interest. The assumption of an isotropic matrix material is also made. The solution also supplies the value of
, (C) being the solute concentration, and provide its distribution in the domain of interest. The assumption of an isotropic matrix material is also made. The solution also supplies the value of ![]() at each point on the upper (or lower) boundary. As a result, the mass flux along this boundary can be calculated as
at each point on the upper (or lower) boundary. As a result, the mass flux along this boundary can be calculated as
![]()
where the subscript (n) indicates numerically computed value, n is the outward unit vector and (L) is the width of the unit cell. Because of impermeable flakes crossing boundaries, which results in sudden local changes of the flux, care must be taken in performing this integration. In this work, we used adaptive intervals and only accepted values of the integral when these were convergent with refinement. Equating this flux with the one obtained from Fick’s law in a macroscopic equivalent cell (whose diffusivity is Deff) we obtain
![]()
where ![]() is the macroscopically imposed concentration difference and (H) the height of the unit cell. These effective diffusivities will be presented and discussed for various values of (
is the macroscopically imposed concentration difference and (H) the height of the unit cell. These effective diffusivities will be presented and discussed for various values of (![]() ), (
), (![]() ) and (
) and (![]() ) in the following sections.
) in the following sections.
3. Results and Discussion
In the following we present the results of a comprehensive computational study of diffusion across doubly-periodic unit cells, each containing up to N = 3000 randomly placed impermeable flakes of rectangular cross-section. In such a system, the orientation of each flake is defined by the orientation angle (θ) formed between the vertical axis (y), which is taken to be the direction of macroscopic diffusion, and the outward normal vector on the flake surface. The horizontal axis is indicated as (![]() ). Parametric studies have shown that for N > 200 the obtained Deff were practically indistinguishable; this conclusion extended for (
). Parametric studies have shown that for N > 200 the obtained Deff were practically indistinguishable; this conclusion extended for (![]() ) as large as 40; therefore most of our computations have been carried out in RVEs containing 500 flake cross sections. We look at systems ranging from dilute to concentrated and in which the fiber orientation (θ) changes between zero (flake orientation perpendicular to the direction of diffusion) to
) as large as 40; therefore most of our computations have been carried out in RVEs containing 500 flake cross sections. We look at systems ranging from dilute to concentrated and in which the fiber orientation (θ) changes between zero (flake orientation perpendicular to the direction of diffusion) to ![]() (fibers oriented along the direction of macroscopic diffusion). We have carried out computations in unit cells similar to those of Figure 1 for
(fibers oriented along the direction of macroscopic diffusion). We have carried out computations in unit cells similar to those of Figure 1 for ![]() and
and ![]() and
and![]() , as well as for
, as well as for ![]() and
and![]() .
.
3.1. Effect of Flake Misalignment on Effective Diffusivity
Representative results of the distribution of (C), also showing the corresponding flake distributions, are shown in Figure 2 and Figure 3.
We define as D11 the diffusivity of such a system when q = 0˚ (all flakes oriented perpendicular to the direction of macroscopic diffusion) and D22 the diffusivity when q = 90˚ (all flakes oriented parallel to the direction of diffusion). D11 and D22 are the principal values of the two-dimensional diffusivity tensor, D. The diffusivity tensor ![]() corresponding to a system in which the flakes assume an orientation angle q (counterclockwise with respect to the x-axis) can be determined according to the relation
corresponding to a system in which the flakes assume an orientation angle q (counterclockwise with respect to the x-axis) can be determined according to the relation ![]() , where
, where ![]() is the rotation tensor (
is the rotation tensor (![]() ,
, ![]() ,
, ![]() ,
,![]() ).
).
Hence
![]() (1)
(1)
Therefore, the effective diffusivity of this system in the direction (y) forming
an angle (![]() ) with the axis of the flakes will be
) with the axis of the flakes will be
![]() (2)
(2)
We will investigate the use of Equation (2) to determine![]() , provided the principal permeabilities D11 and D22 are known. By comparing its predictions to our computational results we will identify which models for D11 and D22 give the best agreement with computation.
, provided the principal permeabilities D11 and D22 are known. By comparing its predictions to our computational results we will identify which models for D11 and D22 give the best agreement with computation.
In the first instance we have compared the computational results for dilute cases (![]() and
and![]() ) with the predictions of Equation (2), in which
) with the predictions of Equation (2), in which
Nielsen’s [2] , model has been used for D11 and D22, namely ![]() and
and![]() .
.
Extensive comparisons have shown that predictions of Equation (2) based on Nielsen’s model for D11 and D22 are close to the computational results only for the very dilute regime (![]() ). For progressively higher of (
). For progressively higher of (![]() ) there is a growing discrepancy.
) there is a growing discrepancy.
It is of course possible to use diffusivity models for D11 and D22 more suitable for concentrated suspensions. A review and evaluation of available models has been carried out by Chen and Papathanasiou [11] . Of the models discussed there, we single out those of Cussler and co-workers [1] [9] mainly because of their relevance to the systems modeled here (randomly placed flakes) as well as due to the small number of adjustable parameters needed in their implementation and their extensive use in the literature. Lape et al. [1] proposed that for diffusion across arrays of unidirectional randomly placed flakes it is
![]()
In deriving this model, the tortuosity factor was taken to be 1 + αφ/3 and it was further assumed that the ratio of the areas available for diffusion is
![]()
Implicit in the above derivation is the assumption that the diffusion paths around a flake form straight lines; therefore it is not unreasonable to treat the factor “3” in the expression above as a geometrical parameter that may be adjusted if so suggested by the data. Since that was found to be the case in analyzing our data, we use the model of Lape et al. [1] in the form:
![]() (3)
(3)
in which (![]() ) is an adjustable geometrical parameter. Another model suitable for concentrated aligned flake systems [9] reads
) is an adjustable geometrical parameter. Another model suitable for concentrated aligned flake systems [9] reads
![]() (4)
(4)
where (![]() ) is also an adjustable geometric factor. The following Figure 4 gives a
) is also an adjustable geometric factor. The following Figure 4 gives a
comparison between the computational results, for flakes with ![]() and for
and for ![]() and
and![]() , in unit cells similar to those of Figure 3 and the predictions of Equation (2), in which D11 is taken from [1] [9] and D22 from [2] . It is evident that use of models for D11 more suitable for concentrated systems results in significantly improved predictions of Deff for all (θ). The model of Lape et al. [1] gives an excellent agreement with the computational results for
, in unit cells similar to those of Figure 3 and the predictions of Equation (2), in which D11 is taken from [1] [9] and D22 from [2] . It is evident that use of models for D11 more suitable for concentrated systems results in significantly improved predictions of Deff for all (θ). The model of Lape et al. [1] gives an excellent agreement with the computational results for ![]() even for
even for ![]() as low as 0.01 (especially away from
as low as 0.01 (especially away from![]() ) with a slight adjustment of
) with a slight adjustment of ![]() to 2.7 at
to 2.7 at![]() , while the model of Cussler et al. [1] gave a very good fit with
, while the model of Cussler et al. [1] gave a very good fit with ![]() at
at![]() . The latter model Equation (4) can also be used at lower (
. The latter model Equation (4) can also be used at lower (![]() ) values with proper adjustment of the parameter (
) values with proper adjustment of the parameter (![]() ); at
); at ![]() best agreement was obtained for
best agreement was obtained for ![]() and at
and at ![]() best agreement was obtained for
best agreement was obtained for![]() . Finally, it is noteworthy that near
. Finally, it is noteworthy that near ![]() (flakes oriented almost parallel to the direction of diffusion) the numerical results are in very close agreement with Equation (2) for all concentrations. Since at
(flakes oriented almost parallel to the direction of diffusion) the numerical results are in very close agreement with Equation (2) for all concentrations. Since at ![]() the term containing D22 dominates, this shows that Nielsen’s model for diffusion parallel to the flakes is a reliable one, even for (αφ) as high as 10.
the term containing D22 dominates, this shows that Nielsen’s model for diffusion parallel to the flakes is a reliable one, even for (αφ) as high as 10.
Additional comparisons for ![]() and higher values of (
and higher values of (![]() ) are shown in Figure 5, in terms of the BIF. There are 50 computational data-points at each value of (
) are shown in Figure 5, in terms of the BIF. There are 50 computational data-points at each value of (![]() ) and those at the same (
) and those at the same (![]() ) almost completely overlap. This has been shown before [11] , namely that spatial randomness has a very small effect on the diffusivity of such systems.
) almost completely overlap. This has been shown before [11] , namely that spatial randomness has a very small effect on the diffusivity of such systems.
In summary, our computational results and the comparisons presented above have shown that the effective diffusivity Deff of a system of randomly placed flakes oriented at an angle (![]() ) with the direction of macroscopic diffusion can be predicted by
) with the direction of macroscopic diffusion can be predicted by
![]() (5)
(5)
where![]() . As explained above, this model is in excellent agreement with the computational data for the entire range of (
. As explained above, this model is in excellent agreement with the computational data for the entire range of (![]() ) and (θ) studied. In addition, we compare the predictions of our model to an experimental result [22] [23] , namely that for small values of the misalignment angle (θ) it is
) and (θ) studied. In addition, we compare the predictions of our model to an experimental result [22] [23] , namely that for small values of the misalignment angle (θ) it is
![]()
in which ![]() corresponds to a composite fully aligned normal to the direction of diffusion. If D11 is the diffusivity of the fully-aligned system, the BIF implied by the above statement will be
corresponds to a composite fully aligned normal to the direction of diffusion. If D11 is the diffusivity of the fully-aligned system, the BIF implied by the above statement will be
![]() (6)
(6)
From Equation (2) it can be seen that the BIF implied by our model, (setting, without loss of generality or relevance, D22~D0~1) is
![]() (7)
(7)
As shown in Figure 6, at each value of (![]() ) the predictions of Equation (7) approach asymptotically those of Equation (6) albeit at progressively higher values of D11 (that is, for more dilute systems) as (
) the predictions of Equation (7) approach asymptotically those of Equation (6) albeit at progressively higher values of D11 (that is, for more dilute systems) as (![]() ) increases. However, the limiting behavior of Equation (7) in the concentrated regime (small D11) suggests a qualitatively different behavior for the BIF. Our computational results support this prediction, as will be elaborated upon in the following section. With reference to Figure 6, if the model of Lape et al. [1] is adopted for D11, a value of
) increases. However, the limiting behavior of Equation (7) in the concentrated regime (small D11) suggests a qualitatively different behavior for the BIF. Our computational results support this prediction, as will be elaborated upon in the following section. With reference to Figure 6, if the model of Lape et al. [1] is adopted for D11, a value of ![]() corresponds to
corresponds to ![]() while a value
while a value ![]() will give
will give![]() . Therefore, our model is consistent with Equation (6) well into the semi-concen- trated regime, for small misalignment angles.
. Therefore, our model is consistent with Equation (6) well into the semi-concen- trated regime, for small misalignment angles.
3.2. The Effect of Flake Concentration
In aligned systems, it is known [1] [9] [10] that the BIF scales with ![]() at higher concentrations, and linearly with
at higher concentrations, and linearly with ![]() in the dilute regime. No such definitive information is available when deviations from perfect alignment occur. Figure 7 shows all our computational results for
in the dilute regime. No such definitive information is available when deviations from perfect alignment occur. Figure 7 shows all our computational results for![]() . It is clear that while the quadratic rise with (
. It is clear that while the quadratic rise with (![]() ) is indeed observed in aligned systems (
) is indeed observed in aligned systems (![]() ), this asymptotic behavior is lost as (θ) increase and the BIF approaches a
), this asymptotic behavior is lost as (θ) increase and the BIF approaches a
![]()
Figure 6. Predictions of Equation (7) (broken lines) showing its asymptotic approach to the experimental result represented by Equation (6) (solid line). Larger values of D11 correspond to more dilute systems.
plateau value; this plateau is lower the larger the misalignment angle (θ) is. The implication of this result is that for the full potential of large-![]() flake systems as diffusion barriers to be realized, good alignment is essential. Also shown in Figure 7 are the predictions of Equation (5); as in Figure 4 and Figure 5 the agreement between the two is excellent.
flake systems as diffusion barriers to be realized, good alignment is essential. Also shown in Figure 7 are the predictions of Equation (5); as in Figure 4 and Figure 5 the agreement between the two is excellent.
3.3. Limiting Behavior of the BIF at Very High (αφ).
In light of the excellent agreement between computational results and Equation (5) it is possible to use the latter to obtain analytical estimates of the leveling-off values of the BIF at each (θ), by observing that the first term of Equation (5) becomes negligible at high (![]() ), leaving
), leaving
![]() (8)
(8)
Figure 8 compares our computational results to the predictions of Equation (8) as well as the approach to that limit based on Equation (5). A conclusion is obvious―the quadratic rise of the BIF with (![]() ) is lost when
) is lost when![]() . For a misalignment as small as 5.7˚ (0.1 rad) the upper limit on the achievable BIF from Equation (13) is 104―a three-fold decrease from the theoretical BIF of a perfectly aligned composite with
. For a misalignment as small as 5.7˚ (0.1 rad) the upper limit on the achievable BIF from Equation (13) is 104―a three-fold decrease from the theoretical BIF of a perfectly aligned composite with ![]() and a multi-fold decrease from an aligned composite of even higher (
and a multi-fold decrease from an aligned composite of even higher (![]() ). In fact, for such concentrated systems the departure from the theoretical BIF can be very rapid at small misalignment angles, as can be inferred from Equation (8). This we show in Figure 9 in which we plot the predictions of Equation (8) along with our computational results for
). In fact, for such concentrated systems the departure from the theoretical BIF can be very rapid at small misalignment angles, as can be inferred from Equation (8). This we show in Figure 9 in which we plot the predictions of Equation (8) along with our computational results for ![]() and
and![]() .
.
The above comments and results are particularly pertinent to high aspect ratio
![]()
Figure 8. The approach to the BIF limit (as predicted by Equation (8), dotted lines) for θ = 0.1, 0.2 and 0.4 (in rad) as well as the predictions of Equation (5) (solid lines). Points are computational results. α = 1000.
![]()
Figure 9. Computed BIF at ![]() as a function of the misalignment angle (θ). With a solid line are shown the predictions of Equation (8). The rate of decline in barrier performance with even a slight misalignment is very significant at small (θ), when (αφ) is large.
as a function of the misalignment angle (θ). With a solid line are shown the predictions of Equation (8). The rate of decline in barrier performance with even a slight misalignment is very significant at small (θ), when (αφ) is large.
flakes, such as found in exfoliated nanoclay or graphene composites, for which even at low (![]() ) a high (
) a high (![]() ) value can be achieved; in our simulations in which
) value can be achieved; in our simulations in which![]() , the maximum
, the maximum ![]() of 40 translates into
of 40 translates into![]() . Evidently, Εquation (8) in that case says that the limiting BIF is only a function of the misalignment angle―and our computations are in complete agreement with this prediction. At higher loadings, Equation (8) predicts that the limiting BIF will increase for larger values of (
. Evidently, Εquation (8) in that case says that the limiting BIF is only a function of the misalignment angle―and our computations are in complete agreement with this prediction. At higher loadings, Equation (8) predicts that the limiting BIF will increase for larger values of (![]() ).
).
4. Conclusion
In this study we proposed a model for the Barrier Improvement Factor (BIF) of misaligned flake composites which is valid up to very high flake concentrations, as could be found in composites fabricated by 3D printing. The model requires as inputs the two principal diffusivities of the composite, normal and parallel to the flake axis. In this respect, we find that the models of Lape et al. [1] and Nielsen [2] form an excellent combination. The simple algebraic form of the proposed model makes it usable without recourse to special computing facilities. This model was tested exhaustively by comparing to predictions of 2D computer simulations which included up to 3000 randomly placed but uniformly oriented flake cross-sections in each RVE. Each cross-section forms an angle (![]() ) with the direction of macroscopic diffusion. Over 1500 simulations were carried out and upon comparison the model was found in agreement with computational results for all misalignment angles and for values of (
) with the direction of macroscopic diffusion. Over 1500 simulations were carried out and upon comparison the model was found in agreement with computational results for all misalignment angles and for values of (![]() ) up to 40. Both our model and our computational data predict that at
) up to 40. Both our model and our computational data predict that at ![]() the quadratic dependence of the BIF on (
the quadratic dependence of the BIF on (![]() ) is lost, with the BIF approaching a plateau at higher values of (
) is lost, with the BIF approaching a plateau at higher values of (![]() ). This plateau is lower as (θ) increases. We derive analytical estimates of this maximum achievable BIF at each level of misalignment; these are also shown to be in excellent agreement with the computational results. Finally we show that our computational results and model are in agreement with experimental evidence at small values of (θ). Future work involves extension to even higher values of (
). This plateau is lower as (θ) increases. We derive analytical estimates of this maximum achievable BIF at each level of misalignment; these are also shown to be in excellent agreement with the computational results. Finally we show that our computational results and model are in agreement with experimental evidence at small values of (θ). Future work involves extension to even higher values of (![]() ) as well as comparison with 3D computations.
) as well as comparison with 3D computations.