An Alternative Approach to the Solution of Multi-Objective Geometric Programming Problems

Ersoy Öz, Nuran Güzel, Selçuk Alp

Yildiz Technical University, Istanbul, Turkey.

DOI: 10.4236/ojop.2017.61002                

Abstract

The aim of this study is to present an alternative approach for solving the multi-objective posynomial geometric programming problems. The proposed approach minimizes the weighted objective function comes from multi-objective geometric programming problem subject to constraints which constructed by using Kuhn-Tucker Conditions. A new nonlinear problem formed by this approach is solved iteratively. The solution of this approach gives the Pareto optimal solution for the multi-objective posynomial geometric programming problem. To demonstrate the performance of this approach, a problem which was solved with a weighted mean method by Ojha and Biswal (2010) is used. The comparison of solutions between two methods shows that similar results are obtained. In this manner, the proposed approach can be used as an alternative of weighted mean method.

Keywords

Multi Objective Geometric Programming, Kuhn-Tucker Conditions, Taylor Series Expansion, Numerical Method, Weighted Mean Method

1. Introduction

Geometric Programming Problem (GPP) is a special type of nonlinear programming that often used in the applications for production planning, personal allocation, distribution, risk managements, chemical process designs and other engineer design situations. GPP is a special technique that is developed in order to find the optimum values of posynomial and signomial functions. In the classical optimization technique, a system of nonlinear equations is generally faced after taking partial derivatives for each variable and equalizing them to zero. Since the objective function and the constraints in the GPPs will be in posynomial or signomial structures, the solution of the system of nonlinear equations obtained by the classic optimization technique will be very difficult. The solution to the GPP follows the opposite method with respect to the classical optimization technique and it depends on the technique of first finding the weight values and calculating the optimum value for the objective function, then finding the values of the decision variables.

GPP has been known and used in various fields since 1960. GPP started to be modeling as part of nonlinear optimization by Zener [1] in 1961 and Duffin, Peterson and Zener [2] in 1967 and particular algorithms were used when trying to solve GPP. After that many important studies were done in various fields: communication systems [3] , engineering design [4] [5] [6] , resource allocation [7] , circuit design [8] , project management [9] and inventory management [10] .

When there are multiple objectives in the GPP, the problem is defined as the Multi-Objective Geometric Programming Problem (MOGPP). In general, there are two types (namely fuzzy GPP and weighted mean method) of solving approaches are exist in the literature. The studies deal with fuzzy GPP method can be given as Nasseri and Alizadeh [11] , Islam [12] , Liu [5] , Biswal [13] , Verma [14] and Yousef [23] . Besides, to solve the multi-objective optimization problem, another and the simplest way is using the weighted mean method. The weighted mean method is also used and applied for the solution of the MOGPP by Ojha and Biswall [15] .

Numerical approximations are widely used to solve the Multi-objective programming problems. One of the numerical approximations is the Taylor series expansion which is also given as a solution method in this study. Toksarı [16] and Güzel and Sivri [17] have used Taylor series to solve the multi-objective linear fractional programming problem and have given examples.

In this study, a numerical approach to solve the multi-objective posynomial geometric programming problems is proposed. This numerical approach minimizes the weighted objective function subject to Kuhn-Tucker Conditions expanded the first order Taylor series expansion about any arbitrary initial feasible solution. The same process is continued iteratively until the desired accuracy is achieved. The solution obtained at the end of the iterative processing gives the pareto optimal solution to solve the multi-objective posynomial geometric programming problem. When the results obtained are compared to the results of the weighted mean method [15] used to solve the multi-objective posynomial geometric programming problems, the same results are found.

In the next section of this study, MOGPP, weighted method for MOGPP and dual form of MOGPP are respectively mathematically explained. In the third section, the model that we suggest depending on the Kuhn-Tucker Conditions and first order Taylor Series expansion will be clarified. Then, the results obtained by weighted mean method and the results obtained by the approach that we suggest will be compared for a numeric example. In the last section, conclusion and comments will be included.

2. Multi-Objective Geometric Programming Problem

2.1. Standard Geometric Programming Problem

Let 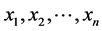show 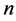real positive variables and a vector with components. A real valued function of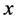, with the form,

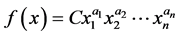(1)

where 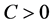and. The function is named a monomial function. A sum of one or more monomial functions is named a posynomial function. The term “posynomial” is meant to suggest a combination of “positive” and “polynomial”. A posynomial function of the term,

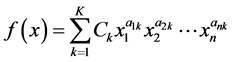(2)

where 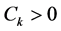and.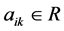

GPP is a problem with generalized posynomial objective and inequality constraints, and monomial equality constraints. Standard form of a GPP can be written as

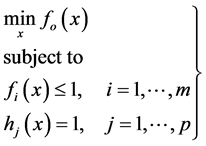(3)

where 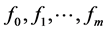are posynomials and 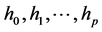are monomials.

GPP in standard form is not a convex optimization problem. GP is a nonlinear, nonconvex optimization problem that can be logarithmic transformed into a nonlinear, convex problem.

Assuming for simplicity that the generalized posynomials involved are ordinary posynomials, it can express a GPP clearly, in the so-called standard form:

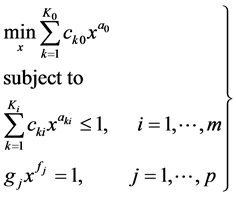(4)

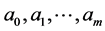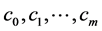where and are vectors in and are vectors with positive components.

Most of these posynomial type GPP’s have zero or positive degrees of difficulty. Parameters of GPP, except for exponents, are all positive and called posynomial problems. GPP’s with some negative parameters are also called signomial problems.

The degree of difficulty is defined as the number of terms minus the number of variables minus one, and is equal to the dimension of the dual problem. If the degree of difficulty is zero, the problem can be solved analytically. If the degree of difficulty is positive, then the dual feasible region must be searched to maximize the dual objective, and if the degree of difficulty is negative, the dual constraints may be inconsistent [15] .

GPP in standard form is not a convex optimization problem. GPP is a nonlinear, nonconvex optimization problem that can be logarithmic transformed into a nonlinear, convex problem.

2.2. Multi-Objective Geometric Programming Problem

General form of multi objective GPP, where p is the number of objective functions which are minimized and n is the number of positive decision variables, is defined as:

(5)

where and are real numbers for all i, k, t, j and for all k and t are positive real numbers, and. The number of terms in the objective function is, and the number of terms in the constraint is. is the set of constraints, considered as non- empty compact feasible region. When all of the C constants are positive, the function is called a posynomial. When at least one of them is negative, it is called a signomial [18] [25] . The model in this study consists only of posynomials. The degree of difficulty is found by subtracting the number of variables in the primal problem plus one from the number of terms in the primal problem. If the degree of difficulty is zero, only one solution will be achieved since the number of equations given under the normality and orthagonality conditions will be equal to the number of unknown terms. When the degree of difficulty is below zero, the dual constraints may be inconsistent. And when the degree of difficulty is above zero, in order to maximize the dual objective, the dual feasible region must be searched [18] [25] .

Definition 1 is a pare to optimal solution of MOGPP (5) if there does not exist another feasible solution such that and at least one.

Definition 2 is a weakly pare to optimal solution of MOGPP (5) if there does not exist another feasible solution such that .

3. The Weighting Method to the Multi-Objective Geometric Programming Problem

General form of multi objective optimization problem can be mathematically stated as:

(6)

where and. is the set of constraints, considered as non-empty compact feasible region.

A multi-objective problem is often solved by combining its multiple objectives into one single-objective scalar function. This approach is in general known as the weighted-sum or scalarization method. In more detail, the weighted-sum method minimizes a positively weighted convex sum of the objectives, that is,

(7)

that represents a new optimization problem with a single objective function. We denote the above minimization problem with.

The following result by Geoffrion [19] states a necessary and sufficient condition in the case of convexity as follows: If the solution set is convex and the objectives are convex on, is a strict Pareto optimum if and only if it exists, such that is an optimal solution of problem. If the convexity hypothesis does not hold, then only the necessary condition remains valid, i.e., the optimal solutions of are strict Pareto optimal [20] .

In order to the above MOGPP defined in problem (5) consider the following procedure of the weighting method, a new minimization type objective function may be defined as:

(8)

4. The Kuhn-Tucker Theorem

The basic mathematical programming problem is that of choosing values of variables so as to minimize a function of those variables subject to inequality constraints:

(9)

This problem is a generalization of the classical optimization problem, since equality constraints are a special case of inequality constraints. By additional variables, called slack variables, , the mathematical programming problem (9) can be rewritten as a classical optimization problem:

(10)

The solution to problem (10) is then analogous to the Lagrange theorem for classical optimization problems. The Lagrange theory for a classical optimization problem can be extended to problem (10) by the following theorem.

Theorem 4.1 Assume that are all differentiable. If the function attains at point a local minimum subject to the set , then there exists a vector of Lagrange multipliers such that the following conditions are satisfied:

(11)

The conditions (11) are necessary conditions for a local minimum of problem. The conditions (11) are called the Kuhn-Tucker conditions.

For proof of theorem, the Lagrange function can be defined as:

(12)

The necessary conditions for its local minimum are

(13)

(14)

(15)

The conditions (11) are obtained from the conditions (12)-(15) [24] .

When there are inequalities constraints in nonlinear optimization problems, Kuhn-Tucker Conditions can be used which are based on Lagrange multipliers. The Kuhn-Tucker Conditions satisfy the necessary and sufficient conditions for a local optimum point to be a global optimum point [21] [22] .

5. Proposed Method to Solve MOGPP

The multi-objective geometric problem (5) as a single objective function using the weighting method can be rewritten as follows:

(16)

The above problem (16) may be slightly modified by introducing new variables, whose values is transformed into single objective GPP as:

(17)

Assume that and are all dif-

ferentiable. The new function is formed by introducing multipliers for to problem (17) according to theorem 4.1 can be defined as

(18)

where at the point, the objective function attaints a local minimum according to theorem (4.1). The optimization problem to minimize the objective function subject to conditions (18) can be rewritten as follows:

(19)

Since the necessary conditions (17) are also the sufficient conditions for a minimum problem if the objective function of the geometric programming pro- blem (19) is convex. Therefore, optimal solution of the problem (19) gives the solution of the problem (16).

The above problem (19) is nonlinear problem since both the objective function and the constraints are nonlinear. We will use the Taylor theorem for the linearization to the problem (19). Let be both the objective function and the constraints have differentiable. Then they are expanded using the Taylor theorem about any arbitrary initial feasible solution and any arbitrary initial feasible values to problem (19). Thus, the problem (19) as the linear approximation problem can be rewritten as follows:

(20)

The linear approximation problem is solved, giving an optimal solution and, a new linear programming problem is derived from the solution and. Linear approximation problem is solved, giving an optimal solution and. The following steps are involved from the initial step till reaching the desired optimal solution or until is as close to zero as possible iteratively. The optimal solution is taken as the pare to optimal solution for MOGPP since solution is better than.

The steps for the proposed solution algorithm are given below:

Step 1: Formulate the given MOGPP is as a single objective GP using the weighting method.

Step 2: Construct the constraints for the new problem from Kuhn-Tucker conditions.

Step 3: Set the nonlinear model taking the single objective function in step 1 and the constraints in step 2 to MOGPP.

Step 4: value denotes the iteration or step number of the proposed iterative approach and and denote the vector parameter assigned to the vector of objective function and constraints in step 1. Take the initial solution, and, arbitrarily.

Step 5: Expanded both the objective function and constraints of the problem obtained in step 3 using first order Taylor polynomial series about and in the feasible region of problem. Reduced the problem obtained in step 3 to a linear programming problem.

Step 6: Solve the problem in step 5. Calculate to the approximate solution and

Step 7: For eps > 0 and eps as close to 0 as possible, if is taken as the pareto optimal solution to MOGPP and the values for the objective functions are calculated. Else, take, go back to step 5.

Numerical example

To illustrate the proposed model we consider the following problem which is also used in [15] .

Find

subject to

The primal problem above can be written as below:

subject to

Using the weights and, the primal problem is written as below:

subject to

where

In this problem, the primal term number is 8, primal variable number is 4 and thus the degree of difficulty is 3.

The dual problem corresponding to the last primal problem is given below:

subject to

and

Problem 1 will now be solved using the proposed model. The value interval for and will be between 0.1 and 0.9. For the weights, the given geometric problem from the Problem 1 is written as

,

subject to

.

Then, the above problem according to the Kuhn-Tucker Conditions can be formulated as in Model 1 as follows:

(21)

From Equation (21) the problem is written as follows:

subject to

,

To linearize the nonlinear objective function with the nonlinear constraints in the above problem, we use the first order Taylor polynomial series at any initial feasible point

as follows:

,

subject to

,

,

The solution of the above problem is

,

and and.

When the same procedure is applied to point, the solution is obtained. If the same iteration continues for the weights, , the calculated solution points and the corresponding objective function values and are given in Table 1. As seen in Table 1, the absolute value of the difference between the points X(5) and X(5) is reduced enough to a smaller value, and the iteration is terminated. One of the points or can be assumed the par to optimal solution point of the given MOGPP for the weights,.

By considering different values of and, the corresponding solutions of the problem applying the taylor approach in each iteration are given in Table 2.

6. Result and Conclusion

In this study, we proposed an alternative approach to the approximate pare to solution of MOGPP based on the weighting method. In this model, MOGPP has been reduced to a sequential linear programming problem and the Pareto optimal solution of MOGPP has been calculated approximately in an easier and more speedy way. Besides in GP problems and MOGPP the solution becomes more difficult when the degree of difficulty is a positive number whereas such a difficulty does not exist in the developed model. The solution for the problem given in the example by the weighted mean method is shown in Table 3 and the

Table 1. The corresponding iteration solution for and, using the Taylor series approach.

Table 2. The solution from the numerical approach method.

Table 3. Primal solutions [15] .

solution by the model that we developed is shown in Table 2 and the results are almost the same. For this reason, proposed method can be used as an alternative of weighted mean method.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Zener, C. (1961) A Mathematical Aid in Optimizing Engineering Design. Proceedings of National Academy of Sciences, 47, 537-539. https://doi.org/10.1073/pnas.47.4.537
[2]	Duffin, R.J., Peterson E.L. and Zener, C. (1967) Geometric Programming: Theory and Application. John Wiley and Sons, New York.
[3]	Chiang, M. (2005) Geometric Programming for Communication Systems. Now Publishers Inc., Boston.
[4]	Choi, J.C. and Bricker, D.L. (1996) Effectiveness of a Geometric Programming Algorithm for Optimization of Machining Economics Models. Computers & Operations Research, 23, 957-961. https://doi.org/10.1016/0305-0548(96)00008-1
[5]	Liu, S.T. (2007) Geometric Programming with Fuzzy Parameters in Engineering Optimization. International Journal of Approximate Reasoning, 46, 484-498. https://doi.org/10.1016/j.ijar.2007.01.004
[6]	Ny, J.L. and Pappas, G.J. (2010) Geometric Programming and Mechanism Design for Air Traffic Conflict Resolution. Proceedings of the 2010 American Control Conference, Baltimore, 30 June-2 July 2010, 3069-3074.
[7]	Elmaghraby, S.E. and Morgan, C.D. (2007) Resource Allocation in Activity Networks under Stochastic Conditions: A Geometric Programming-Sample Path Optimization Approach. Tijdschrift voor Economie en Management, 52, 367-389.
[8]	Chu, C. and Wong, D.F. (2001) VLSI Circuit Performance Optimization by Geometric Programming. Annals of Operations Research, 105, 37-60. https://doi.org/10.1023/A:1013345330079
[9]	Scott, C.H. and Jefferson, T.R. (1995) Allocation of Resources in Project Management. International Journal of System Science, 26, 413-420. https://doi.org/10.1080/00207729508929042
[10]	Jung, H. and Klein, C.M. (2001) Optimal Inventory Policies under Decreasing Cost Functions via Geometric Programming. European Journal of Operational Research, 132, 628-642. https://doi.org/10.1016/S0377-2217(00)00168-5
[11]	Nasseri, S.H. and Alizadeh, Z. (2014) Optimized Solution of a Two-Bar Truss Nonlinear Problem Using Fuzzy Geometric Programming. Journal Nonlinear Analysis and Application, 2014, 1-9. https://doi.org/10.5899/2014/jnaa-00230
[12]	Islam, S. (2010) Multi-Objective Geometric Programming Problem and Its Applications. Yugoslav Journal of Operations Research, 20, 213-227. https://doi.org/10.2298/YJOR1002213I
[13]	Biswal, M.P. (1992) Fuzzy Programming Technique to Solve Multi-Objective Geometric Programming Problems. Fuzzy Sets and Systems, 51, 67-71. https://doi.org/10.1016/0165-0114(92)90076-G
[14]	Verma, R.K. (1990) Fuzzy Geometric Programming with Several Objective Functions. Fuzzy Sets and Systems, 35, 115-120. https://doi.org/10.1016/0165-0114(90)90024-Z
[15]	Ojha, A.K. and Biswal, K.K. (2010) Multi-Objective Geometric Programming Problem with Weighted Mean Method. International Journal of Computer Science and Information Security, 7, 82-86.
[16]	Toksari, M.D. (2008) Taylor Series Approach to Fuzzy Multiobjective Linear Fractional Programming. Information Sciences, 178, 1189-1204. https://doi.org/10.1016/j.ins.2007.06.010
[17]	Güzel, N. and Sivri, M. (2005) Taylor Series Solution of Multi Objective Linear Fractional Programming Problem. Trakya University Journal of Science, 6, 91-98.
[18]	Boyd, S., Kim, S.J., Vandenberghe, L. and Hassibi, A. (2007) A Tutorial on Geometric Programming. Optimization and Engineering, 8, 67-127. https://doi.org/10.1007/s11081-007-9001-7
[19]	Geoffrion, A.M. (1968) Proper Efficiency and the Theory of Vector Maximization. Journal of Mathematical Analysis and Applications, 22, 618-630. https://doi.org/10.1016/0022-247X(68)90201-1
[20]	Caramia, M. and Dell’Olmo, P. (2008) Multi-Objective Management in Freight Logistics. Springer, London.
[21]	Bazaraa, S., Sherali, H.D. and Shetty, C.M. (2006) Nonlinear Programming Theory and Algorithms. 3rd Edition, John Wiley and Sons, New York. https://doi.org/10.1002/0471787779
[22]	Kwak, N.K. (1973) Mathematical Programming with Business Applications. McGraw-Hill, New York.
[23]	Yousef, S., Badra, N. and Abu-El Yazied, T.G. (2009) Geometric Programming Problems with Fuzzy Parameters and Its Application to Crane Load Sway. World Applied Science Journal, 7, 94-101.
[24]	Luptacik, M. (2010) Mathematical Optimization and Economic Analysis. Springer, New York. https://doi.org/10.1007/978-0-387-89552-9
[25]	Ota, R.R. and Ojha, A.K. (2015) A Comparative Study on Optimization Techniques for Solving Multi-Objective Geometric Programming Problems. Applied Mathematical Sciences, 9, 1077-1085. https://doi.org/10.12988/ams.2015.4121029