1. Introduction
The Davydov soliton is a fundamental nonlinear excitation in the bio-system of human being, which has been discovered by the Davydov in 1973 [1] [2] [3] . By improving his model, Pan Xiao-feng presented that the Davydov soliton is the basic transformed unit of energy and information in bio-system included human body [4] [5] . Many facts also reveal that the bio-solitons sometimes can be seen as electrically longitudinal vibrations travelling along proteins, microtubules and DNA, etc., including interfering with local resonant oscillations by excitation of neighboring molecules and macromolecules [6] , for example, C. W. Smith presented a model of ideal cell resonance [7] and Fröhlich presented the coherent oscillation of bio-system in 1978 [8] [9] , etc. However, is it possible that this kind of oscillation as a macro-quantum condensation can take place in our body? This problem is interesting because many theories of acupuncture (even including Qigong and Yoga) believe that the down Dan Tian, i.e. about the middle of the abdomen of the human body, is an important accupoint to store bio-energy, until an internal elixir appears [10] . For a long time the internal elixir is an imaginary matter with unclear physical meaning but still pursued by the thousands and thousands practicers, therefore studying this problem is significant for the investigation of mechanism of acupunctures and relative points for helping innumerable practicers.
So, in previous works we have presented that the Davydov solitons can condense in two or three potential wells for simulating the oscillation of quasiparticles in the accupoints [11] [12] . In this work, we try to further explore the relative micro-mechanism, namely the condensation through many couple of bio-solitons in a well based on the BCS (Bardeen―Cooper―Schrieffer) super- conductor theory extended by the nonlinear operator [13] [14] . Then this model can be used to simulate the creation of internal elixir in the middle of the abdomen of the human body. The meaning of this model is that it provides a mechanism to explain the micro-process of stored bio-energy in our body [15] .
2. Bio-Physical Model
The nonlinear excitations (solitons) are supposed to have a condensation in a well of the belly. This assumption is based on the Chinese medicine theories and Acupuncture theories, and also from the results of the thousands and thousands practicers of Qigong or Yoga over thousands years of the world [10] [15] . Then from mathematical and physical points of view we can find the conditions: 1) If the interactions between the solitons all have the same frequency of vibration; 2) If they all have the same moment (or opposite moment), then it can be proven that the numbers of solitons which take place interaction are more possible than other cases. So for simplicity, we consider a physical model describe this sort of condensation process, i.e. the two solitons with opposite moments are condensed into a couple of solitons by exchanging an imaginary phonon (or phonon soliton). In this case the Hamiltonian can be written by
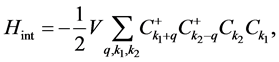 (1)
(1)
where  is defined as a coupling number for a couple of solitons, which is constant;
is defined as a coupling number for a couple of solitons, which is constant;  is a wave vector of a soliton,
is a wave vector of a soliton,
 (2)
(2)
 is a wave vector of a (solitonic) phonon, and
is a wave vector of a (solitonic) phonon, and  is a creation (annihilation) operator of a soliton with
is a creation (annihilation) operator of a soliton with , respectively. Here the quasiparticle is defined as a soliton or a nonlinear excitation generally. So the interaction part of the Hamiltonian can be written as
, respectively. Here the quasiparticle is defined as a soliton or a nonlinear excitation generally. So the interaction part of the Hamiltonian can be written as
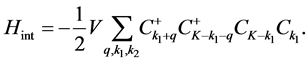 (3)
(3)
Then we can find when , the numbers of the solitons participating scattering process is more larger than other situations, hence the above
, the numbers of the solitons participating scattering process is more larger than other situations, hence the above 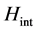 can be written approximately by
can be written approximately by
 (4)
(4)
where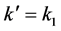 .
.
Therefore, by adding the terms of the energy part for the soliton, the total Hamiltonian can be expressed as
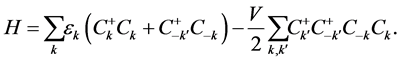 (5)
(5)
3. Diagonalization of Hamiltonian
The Hamiltonian 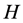 can be firstly simplified by using following forms
can be firstly simplified by using following forms
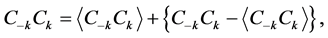 (6)
(6)
 (7)
(7)
and supposing the difference of these operators of the couple of solitons is small value; we therefore can replace the above Equations (6) and (7) into
 and take 1-order of approximation, so the Hamiltonian
and take 1-order of approximation, so the Hamiltonian  is changed as
is changed as
![]() (8a)
(8a)
where we have used
![]() (9)
(9)
Now, by defining
![]() (10)
(10)
the ![]() can be written as
can be written as
![]() (11)
(11)
where notice
![]() (12)
(12)
By applying the Heisenberg equation, we get an equation for![]() ,
, ![]() , respectively,
, respectively,
![]() (13)
(13)
![]() (14)
(14)
For solving these two equations the so-called Bogoliubov transformation is applied,
![]() (15)
(15)
![]() (16)
(16)
where denote that ![]() and
and ![]() are also the nonlinear operators due to
are also the nonlinear operators due to
![]() and
and ![]() are the nonlinear operators, hence the commutation relations are expressed by the so-called Slash product [13] [14] ,
are the nonlinear operators, hence the commutation relations are expressed by the so-called Slash product [13] [14] ,
![]() (17)
(17)
and
![]() (18)
(18)
For example, for the nonlinear operator![]() ,
, ![]() , we can define a slach product as
, we can define a slach product as
![]() (19)
(19)
Then all properties of the linear operator can be applicable to the![]() . Hence by replacing Equations (15) and (16) into the above equations we can get a necessary condition as
. Hence by replacing Equations (15) and (16) into the above equations we can get a necessary condition as
![]() (20)
(20)
So, Equations (15) and (16) can be inverted as
![]() (21)
(21)
![]() (22)
(22)
by replacing Equations (21) and (22) into the Hamiltonian (11), we get
![]() (23)
(23)
where notice again that the Slach product has been introduced. So if let the off-diagnal term in ![]() be equal to zero, we have
be equal to zero, we have
![]() (24)
(24)
then by use Equations (20) and (24) we can obtain
![]() (25)
(25)
where
![]() (26)
(26)
and
![]() (27)
(27)
Hence, we have
![]() (28)
(28)
![]() (29)
(29)
These allow us to obtain the diagnalized Hamiltonian as
![]() (30)
(30)
where the energy of basic state is expressed by
![]() (31)
(31)
and the excitation energy is
![]() (32)
(32)
so ![]() is a energy gap for realizing the condensation, and
is a energy gap for realizing the condensation, and ![]() is the energy of a soliton with the wave vector
is the energy of a soliton with the wave vector![]() .
.
4. The Calculation of ![]()
When the system arrives at the lowest condensation temperature ![]() we must have the number of the couple of solitons is zero, so
we must have the number of the couple of solitons is zero, so
![]() (33)
(33)
then we get
![]() (34)
(34)
and
![]() (35)
(35)
where denote
![]() (36)
(36)
By considering Equations (28) and (29) replaced into Equation (36) to cancel![]() , we get
, we get
![]() (37)
(37)
finally we can get
![]() (38)
(38)
and
![]() (39)
(39)
where ![]() is the Eular number, about 0.5772, so
is the Eular number, about 0.5772, so ![]() is about 1.13. Normally
is about 1.13. Normally
for bio-solitons condensation in our body the temperature ![]() should make sense at room temperature, namely
should make sense at room temperature, namely
![]() (40)
(40)
where the bio-system can regulate the![]() ,
, ![]() and
and ![]() automatically to enable
automatically to enable ![]() in the interval of room temperature. On the other hand, since
in the interval of room temperature. On the other hand, since
![]() ,
, ![]() so, when
so, when ![]() increases,
increases, ![]() decreases; this means when temperature increase the realization of the couple of bio-solitons is easier than temperature decrease. Moreover, because the momentum of the couple of solitons are invariant, therefore the velocities of their movements are invariant without resistance from the medium.
decreases; this means when temperature increase the realization of the couple of bio-solitons is easier than temperature decrease. Moreover, because the momentum of the couple of solitons are invariant, therefore the velocities of their movements are invariant without resistance from the medium.
5. Big Soliton
Furthermore if we assume that ![]() is complex number described by
is complex number described by
![]() (41)
(41)
then![]() , and
, and ![]() are also complex. Then using the same approach as the above we can get
are also complex. Then using the same approach as the above we can get
![]() (42)
(42)
then since ![]() and
and ![]() are all real numbers, so the complex numbers
are all real numbers, so the complex numbers ![]()
and ![]() have the same phase
have the same phase![]() . Then from the spectral decomposition of the diagonalized Hamiltonian (30) we can find that the wave functions of the couple of solitons also share the same phase
. Then from the spectral decomposition of the diagonalized Hamiltonian (30) we can find that the wave functions of the couple of solitons also share the same phase![]() , therefore a highly ordered couple of solitons can be supposed by using a wave function to describe
, therefore a highly ordered couple of solitons can be supposed by using a wave function to describe
![]() (43)
(43)
where defining
![]() (44)
(44)
Then in the situation of no external field condition, which is just a suitable condition for the oscillation inside of the belly, we have the density of the free energy expressed as
![]() (45)
(45)
then applying the principle of minium of the free energy we get
![]() (46)
(46)
which allows us to have
![]() (47)
(47)
This is just a kind of Ginzburg and Landau equation which can describe a soliton. For example in the three dimensional case we can have
![]() (48)
(48)
where defining
![]() (49)
(49)
Then the solution of Equation (48) can be gotten by
![]() (50)
(50)
where notice ![]() is defined as the coherent length, namely
is defined as the coherent length, namely
![]() (51)
(51)
This ![]() is just a soliton! This shows that the gathering of the couple of solitons in the well can form a big soliton, which means the condensation of the many solitons finally can form a big bio-soliton with the oscillation in the well of bio-system.
is just a soliton! This shows that the gathering of the couple of solitons in the well can form a big soliton, which means the condensation of the many solitons finally can form a big bio-soliton with the oscillation in the well of bio-system.
6. Conclusion
A couple of bio-solitons condensation has been presented. The two solitons with opposite moments are condensed into a couple of solitons by exchanging imaginary phonons. Then these couple of solitons can form a big soliton with oscillation. The process can be taken place in the room temperature, and the higher temperature makes the realization easier than lower temperature. This model can be used to simulate the bio-energy stored in our body such as the middle of abdomen of the human body, and also provides a kind explanation of mechanism for the internal elixir formation. This means that the so called internal elixir may be formed through the macro-quantum condensation of a couple of solions, and then the condensation plays a sort of oscillation as a big (or macro-) soliton.