A Mathematical Interpretation of Hawking’s Black Hole Theory by Ricci Flow* ()
1. Introduction and Mathematical Model of the Black Hole
In the paper [1] posted on the arXiv preprint server on January 22, 2014, S. W. Hawking, who is the physicist of University of Cambridge, one of the creators of modern black-hole theory, does away with the notion of an event horizon, the invisible boundary thought to shroud every black hole, beyond which nothing, not even light, can escape.
In its stead, Hawking’s radical proposal is a much more benign “apparent horizon”, which only temporarily holds matter and energy prisoner before eventually releasing them, albeit in a more garbled form (see [2] for details).
Hawking believes that, there is no escape from a black hole in classical theory, but quantum theory enables energy and information to escape from a black hole. Thus a full explanation of the process would require a theory that successfully merges gravity with the other fundamental forces of nature, which is a goal that has eluded physicists for nearly a century.
The Ricci flow equation, introduced by R. Hamilton in [3], is the evolution equation
(1)
for a Riemannian metric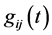
. In his seminal paper, Hamilton proved that this equation has a unique solution for a short time for an arbitrary (smooth) metric on a closed manifold. The Ricci flow theory has been extensively studied by Hamilton and others in a program to understand the topology of manifolds. In particular, in three remarkable papers [4] [5] [6] in 2003, G. Perelman significantly advanced the theory of the Ricci flow, and proved the famous Poincaré conjecture: every closed smooth simply connected three-dimensional manifold is topologically equivalent to a sphere.
In this paper, using the Ricci flow theory introduced by Hamilton, in particular, Perelman’s entropy formula and no local collapsing theorem in [4] and the geometric interpretation of Hamilton’s Harnack expressions by Chow and Chu in [8], by Perelman in [4], we present a mathematical interpretation of Hawking’s black hole theory. In fact, we deal with our mathematical interpretation based on the following hypothesis.
Hypothesis 1.1 (Evolution of the black hole) The evolution of a black hole follows the dynamical system of Hamilton’s Ricci flow (1).
The paper is organized as follows. In section 2, we use Perelman’s entropy formula along the Ricci flow to research the entropy of black holes. In section 3, we recall some facts about Perelman’s no local collapsing theorem and discuss the singularity of the black hole. In section 4, we present the relationship between Hamilton’s Harnack expressions along the Ricci flow and the event horizon of the black hole. In section 5, we present a more magical and wonderful mathematical model of the black hole using Perelman’s 
-geometry. In section 6, using Thurston’s geometrization conjecture, we investigate the evolution of black holes.
2. The Entropy of Black Holes
Firstly, if we assume that the evolution of the black hole follows Hamilton’s Ricci flow system, then we can define the entropy of black holes as follows, which were firstly introduced by Perelman in view of mathematics in [4].
Definition 2.1 (The entropy of black holes) The entropy of black holes are defined as Perelman’s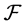 
functional and 
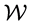functional as follows:
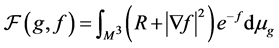(2)
and
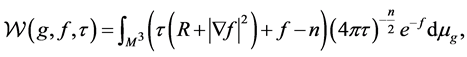(3)
where 
is a Riemannian metric, f is a function on the black hole manifol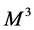d 
and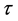 
is a scale parameter.
Then we have two monotonicity formulas for the Ricci flow by Perelman in [4], which implies that the entropy of black holes increases monotonically with time t.
Theorem 2.2 (Monotonicity formulas of the entropy of black holes) Under the evolution system of black holes
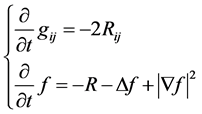(4)
we have the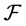 
entropy of black holes increase monotonically with time t
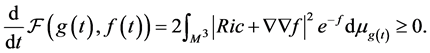(5)
Furthermore, under the system
(6)
we have the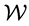 
entropy increase monotonically with time t
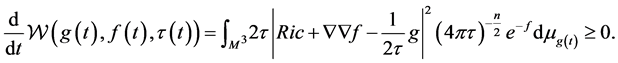(7)
Remark 1. Moreover, according to Bekenstein’s theory of the black hole entropy in [9]: the entropy of a black hole is proportional to its event horizon, Theorem 2.2 implies that the event horizon of a black hole will swell and grow larger than the apparent horizon.
3. No Local Collapsing Theorem and the Singularity of the Black Hole
In order to prove Poincaré conjecture, Perelman in [4] introduced a useful notion of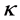 
-noncollapsed as follows.
Definition 3.1 (![]()
-noncollapsed). Given ![]()
and![]()
, we say that a Riemannian manifold ![]()
is ![]()
-noncollapsed below the scale ![]()
if for any metric ball ![]()
with ![]()
satisfying ![]()
for all we have
![]()
(8)
Remark 2. Note that if given![]()
, we define![]()
, then the condition ![]()
for any ![]()
is equivalent to
![]()
(9)
for all![]()
. Moreover, ![]()
is equivalent to
![]()
(10)
In [4], using his ![]()
functional and ![]()
functional, Perelman proved the following no local collapsing theorem, which is the key point in the proof of Poincaré conjecture.
Theorem 3.2 (Perelman’s no local collapsing) Let![]()
, ![]()
be a solution to the Ricci flow on a closed manifold![]()
. If![]()
, then for any ![]()
there exists ![]()
such that ![]()
is ![]()
-non- collapsed below the scale ![]()
for all![]()
.
We now turn back to physics and give the physical correspondence of the above results, here we refer to the paper [2]. In a thought experiment [10], the theoretical physicist J. Polchinski of the Kavli Institute and his colleagues asked what would happen to an astronaut unlucky enough to fall into a black hole. Event horizons are mathematically simple consequences of Einstein’s general theory of relativity that were first pointed out by the German astronomer K. Schwarzschild in a letter he wrote to Einstein in late 1915. In that picture, physicists had long assumed, the astronaut would happily pass through the event horizon, unaware of his or her impending doom, before gradually being pulled inwards-stretched out along the way, like spaghetti-and eventually crushed at the “singularity”, the black hole’s hypothetical infinitely dense core.
Moreover, if we assume that the black hole evolves with the time t along the Ricci flow, then Perelman’s no local collapsing (8) or (10) in Theorem 3.2 implies the following fact.
Theorem 3.3 (Nonexistence of singularity of the black hole) The theorized singularity of the black hole core with infinitely small size and infinite density cannot exist.
Remark 3. This idea presents a mathematical interpretation of the following physical analysis of the “singularity” of black holes together with the laws of quantum mechanics.
Quantum theory dictates that the event horizon must actually be transformed into a highly energetic region, or “firewall”, that would burn the astronaut to a crisp. This was alarming because, although the firewall obeyed quantum rules, it flouted Einstein’s general theory of relativity. According to that theory, someone in free fall should perceive the laws of physics as being identical everywhere in the Universe-whether they are falling into a black hole or floating in empty intergalactic space.
4. Event Horizon of the Black Hole
In this section, we research the event horizon of the black hole, and recall some facts about the Hamilton’s Harnack expressions along the Ricci flow firstly. Define the 3-tensor P by
![]()
which is consider P as a section of the bundle ![]()
of 2-forms tensor product 1-forms, since P is antisymmetric in i and j. Define the symmetric 2-tensor M by:
![]()
where![]()
, where we use the Einstein summation convention. In order to analysis of the singularity for the Ricci flow, Hamilton proved the following useful differential Harnack inequality [11].
Theorem 4.1 (Hamilton) If ![]()
is a solution to the Ricci flow with semi-positive curvature operator and either ![]()
is compact or complete with bounded curvature, then for any 1-form ![]()
and 2-form ![]()
we have
![]()
(11)
In particular, Hamilton noticed the following fact:
The geometry would seem to suggest that the Harnack inequality is some sort of jet extension of positive curvature operator on some bundle including translation as well as rotation, and this is somehow all related to solitons where the solution moves by translation.
Based on Hamilton’s observation, in [8], B. Chow and S.-C. Chu derived a geometric interpretation of Hamilton’s Harnack expression along the Ricci flow. We now recall some facts about this geometric interpretation.
Consider the tangent bundle of the space-time manifold![]()
, where ![]()
is the time interval of existence of the solution to the Ricci flow. Given![]()
, let![]()
, define a degenerate metric ![]()
on cotangent space ![]()
by
![]()
(12)
for![]()
, where ![]()
is the inverse of the metric g. Then define the connection ![]()
on ![]()
by
![]()
(13)
for![]()
.
When deal with the geometry of the space-time manifold ![]()
, Chow and Chu derived the following geometric interpretation of Hamilton’s Harnack expression along the Ricci flow [8].
Theorem 4.2 (Chow-Chu) The Riemannian curvature tensor ![]()
of ![]()
at ![]()
is the same as the Harnack quantity
![]()
(14)
at![]()
.
Chow and Chu’s geometric interpretation of Hamilton’s Harnack expression has profound physical significance. Recall that in quantum mechanics, the uncertainty principle says that, any of a variety of mathematical inequalities asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle known as complementary variables, such as position x and momentum p, or energy E and time t can be known simultaneously.
In particular, in 1927, W. Heisenberg stated that the more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa as follows
![]()
An equivalent expression is that the more precisely the energy of some particle is determined, the less precisely its time can be known as follows
![]()
(15)
When assume that the evolution of the black hole follows Hamilton’s Ricci flow system, we can deal with the geometry of the space-time manifold ![]()
. Note that Theorem 4.1 and 4.2 imply that the Riemannian curvature tensor![]()
, i.e., the Harnack quantity Z bounded by lower, which is very similar to the uncertainty principle. This observation leads us to propose the following claim.
Claim 4.3 (Relationship between Harnack quantity and uncertainty principle) The Hamilton’s Harnack inequality in mathematics is equivalent to the uncertainty principle in physics, moreover, the Harnack quantity
![]()
i.e., the Riemannian curvature tensor ![]()
of![]()
, is the same as the coupling product of energy E and time t.
Recall that Heisenberg considered atomic theory should be based on observable quantity, rather than on some of the concepts from the virtual experience. Thus based on Claim 4.3, we should define the event horizon of the black hole by using “computable and observable quantity”, following Heisenberg’s program.
Definition 4.4 (Event horizon of the black hole) The event horizon of the black hole can be defined by![]()
, where Z is the Harnack quantity (14).
Remark 4. This idea is based on the following consideration: The Harnack quantity Z is the same as the Riemannian curvature tensor ![]()
of
![]()
, which is the reciprocal of the radius of curvature. Thus the event horizon of the black hole is proportional to the radius of curvature, which
can be defined by![]()
.
5. A More Magical and Wonderful Mathematical Model of the Black Hole
In this section, we present a more magical and wonderful mathematical model of the black hole. In particular, we consider the manifold ![]()
with the following metric as the mathematical model of black hole, which was constructed by Perelman in [4]:
![]()
(16)
where ![]()
denote coordinate indices on the ![]()
factor, ![]()
denote those on the ![]()
factor, and the coordinate ![]()
on ![]()
has index 0; ![]()
evolves with ![]()
by the backward Ricci flow
![]()
(17)
![]()
is the metric on ![]()
of constant curvature![]()
.
The manifold ![]()
with the Riemannian metric (16) implies that the visible reality 3-dimensional part ![]()
of the black hole ![]()
evolves with the time t along the Ricci flow. Moreover, the metric of the time variable t is affected by the scalar curvature R, which reflects the time warp effect of general relativity. It is worth noting that some hidden dimensions N curled up in ![]()
(as superstring theory saying).
Remark 5. As noted above, a black hole is actually a dynamical system evolving along Ricci flow together with some curled up dimensions.
6. Evolution of the Black Hole
In mathematics, Thurston’s geometrization conjecture states that certain three- dimensional topological spaces each have a unique geometric structure that can be associated with them (see [12] for details). Using Hamilton’s Ricci flow and Perelman’s breakthrough, J. Morgan and G. Tian present a complete proof of the geometrization conjecture in [13].
Theorem 6.1 (Thurston’s Geometrization) Every closed 3-manifold has a prime decomposition: this means it is the connected sum of prime 3-manifolds (this decomposition is essentially unique except for a small problem in the case of non-orientable manifolds), which cannot be written as a non-trivial connected sum. There are 8 possible geometric structures in 3 dimensions:
1) Spherical geometry![]()
,
2) Euclidean geometry![]()
,
3) Hyperbolic geometry![]()
,
4) The geometry of![]()
,
5) The geometry of![]()
,
6) The geometry of the universal cover of![]()
,
7) Nil geometry,
8) Sol geometry.
Thus, based on Hamilton’s Ricci flow and Thurston’s Geometrization, we can deal with the evolution of the black hole as follows.
Theorem 6.2 (Evolution of the black hole) Every black hole will evolve with time t into a closed 3-manifold with a prime decomposition: the connected sum of prime 3-manifolds, which cannot be written as a non-trivial connected sum with one of the following 8 possible geometric structures: 1)![]()
, 2)![]()
, 3)![]()
, 4)![]()
, 5)![]()
, 6)![]()
, 7) Nil geometry, 8) Sol geometry.
NOTES
![]()
*This work is supported by the National Natural Science Foundation of China (NSFC) 11301493.