Study on Sinking-Sliding Failure Mechanism of Perilous Rock at Wangxia in Three Gorges of the Yangtze River, China ()
1. Introduction
As one of global mountain hazards, collapse stemes from perilous rock and possesses some fundamental characteristics, such as outburst, celerity and disaster [1]. Wangxia perilous rock, locating at the left bank of the Yangtze River in Wu Gorge, proceeded catastrophe sliding failure in July, 2010, since the slow deformation from 1999 and it badly affected the navigation safety of the Yangtze River channel. Hitherto, dynamics characteristic of the perilous rock is an important link for the disaster prevention and mitigation in mountain region at all times and it has been highly concerned by domestic and foreign scholars. Such as, Mitchell et al. proposed a mountain evolution model by simultaneous consideration on tectonic movement and climate effect and discovered that the collapse process with high strength and low frequency had distinct contribution rate in physiognomy evolvement [2]. Blasio discovered that the effective friction coefficient would decrease gradually with the accretion of collapse volume and the rheological properties at the bottom of collapse accumulation turned into non Newtonian fluid from Kulun friction body [3]. Manzella and Labiouse found out that the initial volume size decided the impact distance of avalanche mass and the indoor model test for development process of collapse accumulation with small scale was conducted [4]. Based on the investigation in
Mt.
Tianshan
area, Strom and Korup convinced that strong earthquake was the basic factor for the development of giant rock slope failure and indicated that to distinguish the potential position, volume size, motion characteristic and disaster property was one of the core work to engage the study of mountainous geology and geotechnical engineering [5]. According to the combination of field observation and numerical simulation, Dorren et. al. proposed comprehensive analysis method to forecast collapse source, rockfall route and impact area [6]. Based on geomorphology, Chen et al. analyzed the formation mechanism for the landslip disaster of rocky mountainous region [7] and investigated the mechanical mechanism for the countermarch evolvement of rock slope [8] [9]; For a single perilous rock mass, Chen et al. constructed a damage model for the dominant fissure of perilous rock [10] and established a stability analysis method for perilous rock to fracture [11]. However, those studies before do not show sufficient consideration on the catastrophe failure characteristic of perilous rock and it result in the lack of necessary scientific basis on the safety alarm and risk evaluation of perilous rock and collapse hazard. In this paper, this study takes the W2 block of Wangxia perilous as an example to analyze the catastrophe failure mechanism [12] [13] so as to obtain corresponding dynamic parameters for perilous rock to fracture suddenly. The study maybe provide some practical significance for the disaster prevention and mitigation of Wangxia perilous rock or some similar perilous rock and collapse hazard.
2. Characteristics for the Failure of Wangxia Perilous Rock
The height for the top of Wangxia perilous rock varies from 1220 m a.s.l. to 1230 m a.s.l and for the base of the perilous rock is from 1137 m a.s.l to 1147 m a.s.l., with about 70 m elevation difference. Length of the perilous rock along the cliff is about 120 m, the average thickness is 30 - 35 m, and the volume is about 40 × 104 m3. Based on exist position, Wangxia perilous rock can be divided into two parts/blocks, marking with W1 and W2, respectively (Figure 2). Further, W1 is an isolated pillar, about 65 m with height, 8 m with length, 6 m with width, and 3200 m
3 in
volume. For W2, whose height is about 70 m, length is about 80 m, thickness is 10 - 15 m, volume is about 7 × 104 m3 and the dominant fissure at its tail is transfixed and composed by moniliform solution funnels. The section of the perilous rock is locked patch and it can be divided into upper segment and lower segment. The upper segment is composed by the siliceous and argillaceous limestone layer with different thickness from thin to medium thick and the chert layer, where, its lithology is flinty and it can be simplified as elastic segment. As for the lower segment, it is composed by argillaceous shale and mudstone, possessing strain-softening characteristic, can be simplified as strain-softening segment.
Wangxia perilous rock appeared deformation between Jul. and Aug. in 1999 for the first time, then, it has been actualized professional monitoring by 2003 and it didn’t appear distinct deformation by Jul. 2010. However, on Aug. 21, 2010, due to heavy rainfall in Wu Gorge area, W2 of Wangxia perilous rock appeared aggravation of deformation at the east segment of the perilous rock, the surface layer of the perilous rock fell its blocks frequently with 8 to 40 m
3 in
volume for single block. At 7:
40 a
.m. on Oct. 21, 2010, W2 proceeded catastrophe rupture, whose base slid forth for 10 - 15 m, the whole perilous rock mass dislocated down for about 10 m, it impulsed the soil body at the base of cliff to slid down to the downside of highway, and then, volumes of soil body and rock blocks collapsed down along the slope (Figure 1, Figure 2). This study takes W2 of the perilous rock as an object to explore the catastrophe rupture mechanism of Wangxia perilous rock.
3. Mechanical Model for the Failure of Wangxia Perilous Rock
The geological section of W2 of Wangxia perilous rock is shown as in Figure 3, and the mechanical model is constructed (Figure 4). Simplify the un-linking patch, namely, locked patch, in lower segment of dominant fissure into a beeline, where, which parallels to the dominant fissure is designated x-axis, then, the coordinates xoy is constructed as in Figure 4. The deadweight of perilous rock is mg and the earth pressure of colluvial deposits filled in the linking patch of dominant patch is F. Thus, its components along x-axis are 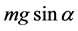 and
and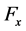 ,
,
![]()
Figure 1. Outline of Wangxia perilous rock before rupture.
![]()
Figure 2. Outline of Wangxia perilous rock after rupture.
![]()
Figure 3. Geological section of Wangxia perilous rock.
respectively, and the components along y-axis are 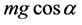 and
and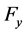 , respectively. Futher, the tangential resistance T and the normal resistance N of locked patch in dominant fissure can be calculated in formula (1) and (2), respectively.
, respectively. Futher, the tangential resistance T and the normal resistance N of locked patch in dominant fissure can be calculated in formula (1) and (2), respectively.
![]()
Figure 4. Mechanical model of Wangxia perilous rock.
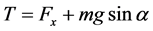 (1)
(1)
 (2)
(2)
where, m is the weight of perilous rock (kg); α is the dip angle for the un-linking patch of dominant fissure (˚); g is the acceleration of gravity (9.8 m/s2).
The constitutive models for elastic segment and strain-softening segment of dominant fissure in Wangxia perilous rock are respectively described by using Equation (3) and Equation (4), and its representative constitutive curves are expressed in Figure 5.
 (3)
(3)
 (4)
(4)
where, G1 is the shear modulus of elastic segment (MPa); 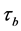 is the residual shear strength of elastic segment (MPa); u is the shear displacement of perilous rock mass (m);
is the residual shear strength of elastic segment (MPa); u is the shear displacement of perilous rock mass (m); 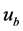 is the critical displacement for elastic segment at the sheared moment (m); h is the thickness of locked patch (m); G2 is the shear modulus of strain-softening segment (MPa); u0 is the corresponding displacement for the peak point of shearing strength on perilous rock mass (m).
is the critical displacement for elastic segment at the sheared moment (m); h is the thickness of locked patch (m); G2 is the shear modulus of strain-softening segment (MPa); u0 is the corresponding displacement for the peak point of shearing strength on perilous rock mass (m).
The permeability of water for the linking patch of dominant fissure at the tail of Wangxia perilous rock is larger, the rock mass in locked patch ruptures and under the effect of groundwater, its intensity is easily to appear weakening-water phenomenon. According to the achievement that intensity of quartzose, shale will change with different moisture content from Vutukuri et al. [14], it describes the effect on the locked patch of Wangxia perilous rock in vierws of groundwater by using weakening-water function g(Sr), as follows.
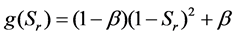 (5)
(5)
![]()
Figure 5. Constitutive curves for two kinds of mediums.
where, Sr is the saturation of rock and soil medium in dominant fissure; g(Sr) is the decreasing function, when the rock and soil sediment in dominant fissure is at the dry state, Sr = 0, g(Sr) = 0, and when it is at the saturation state, Sr = 1, g(Sr) = β; β is the shear strength parameter as the rock and soil sediment in dominant fissure is at the saturation state, the smaller numerical value, the more obvious degradation. β for the elastic segment and strain-sof- tening segment of dominant fissure in Wangxia perilous rock are respectively 0.8 and 0.2.
To substitute Equation (5) into Equation (3), the constitutive model of elastic segment in the locked patch of dominant fissure under the consideration of weakening-water effect is expressed as,
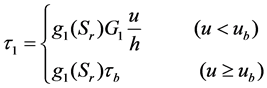 (6)
(6)
where, g1(Sr) is the weakening-water function in the elastic segment of dominant fissure;  is the shearing stress of elastic segment (MPa); other variables are the same as above.
is the shearing stress of elastic segment (MPa); other variables are the same as above.
To substitute Equation (5) into Equation (4), the constitutive model of strain-softening segment in the locked patch of dominant fissure under the consideration of weakening-water effect is expressed as,
![]() (7)
(7)
where, g2(Sr) is the weakening-water function in the strain-softening segment of dominant fissure; ![]() is the shearing stress of strain-softening segment (MPa); other variables are the same as above.
is the shearing stress of strain-softening segment (MPa); other variables are the same as above.
4. Dynamic Parameters for the Failure of Wangxia Perilous Rock
4.1. The Cusp Catastrophe Model for the Failure of Perilous Rock
To perilous rock with unit width, when the locked patch of dominant fissure produces creep displacement u and before it reaches the peak of shear resistance, namely, ![]() , the elastic deformation energy produced by elastic segment is estimated in the following formula.
, the elastic deformation energy produced by elastic segment is estimated in the following formula.
![]() (8)
(8)
where, S1 is the length for the elastic segment in the locked patch of dominant fissure (m); other variables are the same as above.
When the creep displacement u producing by the locked patch of dominant fissure is![]() , and the residual shear strength of elastic segment is
, and the residual shear strength of elastic segment is![]() , the formula to estimate the elastic deformation energy of perilous rock is established as follows.
, the formula to estimate the elastic deformation energy of perilous rock is established as follows.
![]() (9)
(9)
The variables in formula (9) are the same as above.
For the strain-softening segment in the locked patch of dominant fissure, the formula to estimate the elastic deformation energy of perilous rock is established as follows.
![]() (10)
(10)
where, S2 is the length for the strain-softening segment in the locked patch of dominant fissure (m); other variables are the same as above.
The formula to estimate gravitational potential energy of perilous rock mass is as followings.
![]() (11)
(11)
The variables in formula (11) are same as above.
When the medium layer of dominant fissure produces creep displacement u, locked patch accumulates elastic deformation energy and the gravitational potential energy of perilous rock mass is in release state, the potential function of perilous rock mass can be divided into two cases to discuss, respectively.
Case 1: combining Equation (8) with Equations (10) and (11), the formula to express potential function W1 of perilous rock is established, as follows.
![]() (12)
(12)
Case 2: combining Equation (9) with Equations (10) and (11), the formula to express potential function W2 of perilous rock is established, as follows.
![]() (13)
(13)
Taking partial derivative on Equation (12) and Equation (13), respectively. Then
![]() (14)
(14)
![]() (15)
(15)
According to the catastrophe theory, dW/du = 0 is the catastrophe manifold. Based on the quality of smooth manifold, the third-order partial derivative for potential function of perilous rock is gained as![]() , hereby,
, hereby,![]() . To expand the equilibrium surface expressing in Equation (14) at ut by using Taylor integration method and take the value to third-order terms as followings.
. To expand the equilibrium surface expressing in Equation (14) at ut by using Taylor integration method and take the value to third-order terms as followings.
![]() (16)
(16)
where, ![]() is the corresponding displacement for the inflexion of constitutive curve in the strain-softening segment of dominant fissure (m); Other variables are the same as above.
is the corresponding displacement for the inflexion of constitutive curve in the strain-softening segment of dominant fissure (m); Other variables are the same as above.
In the same way, to expand Equation (15) at ut by using Taylor integration method and take the value to third-order terms as,
![]() (17)
(17)
As u < ub, Equation (16) is coordinated as followings,
![]() (18)
(18)
Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , Equation (18) can be simplified as the standard
, Equation (18) can be simplified as the standard
equation of cusp catastrophe model:
![]() (19)
(19)
To substitute parameters![]() ,
, ![]() and
and ![]() into formula b1, and combine Equation (6) with Equation (7), another expression for parameter b1 is established.
into formula b1, and combine Equation (6) with Equation (7), another expression for parameter b1 is established.
![]() (20)
(20)
In catastrophe theory, parameter b1 can be used to distinguish the creep state of perilous rock, discussed as follows from three aspects:
The first, b1 > 0 expresses that the creep acceleration of dominant fissure is less than zero and the deformation of perilous rock is at state of decelerated creep.
The second, b1 = 0 expresses that the creep acceleration of dominant fissure is equal to zero and the deformation of perilous rock is at state of constant creep.
And the third, b1 < 0 expresses that the creep acceleration of dominant fissure is more than zero and the deformation of perilous rock is at state of accelerated creep.
Obviously, u < ub means that perilous rock is at creep state and catastrophe failure does not appear, however, u ≥ ub means some other valuable conclusions, discussing in detail as follows.
when u ≥ ub, Equation (17) is coordinated as Equation (21).
![]() (21)
(21)
Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , Equation (21) can be simplified as the standard equation of cusp catastrophe model.
, Equation (21) can be simplified as the standard equation of cusp catastrophe model.
![]() (22)
(22)
To substitute parameters k2 and ![]() into formula b2, and combine Equation (6) with Equation (7), the another expression for parameter b2 is established.
into formula b2, and combine Equation (6) with Equation (7), the another expression for parameter b2 is established.
![]() (23)
(23)
The physical meaning of parameter b2 is the same as parameter b1.
In addition, in the state u ≥ ub, perilous rock is likely to produce catastrophe failure and the governing equation that catastrophe point to obey is established, as follows.
![]() (24)
(24)
To substitute parameters a2 and b2 into Equation (24), then
![]() (25)
(25)
The smooth catastrophe manifold figure M shown in Figure 6 can be achieved by Equation (22). The two folds of cusp fold in equilibrium surface represents the singular set S, composing of the points with vertical tangent. The projection of singular set S in the a2-b2 plane is called bifurcation set expressed as
![]()
Figure 6. Cusp catastrophe of perilous rock failure.
B1 and B2, respectively. Each point in equilibrium surface, namely, the phase point, denotes a certain status in the evolution process of perilous rock. Further, equilibrium surface can be divided into three parts, i.e., superior leaf, middle leaf and inferior leaf.
4.2. Dynamic Parameters for the Failure of Perilous Rock
The state variable x of cusp catastrophe is instable at the critical points set of vertical tangent in equilibrium surface from inferior leaf to superior leaf. The state variable in critical points set needs to fit in with the Equation as follows,
![]() (26)
(26)
Instability needs to span the left branch B1 of bifurcation set, and then, three roots of Equation (22) are solved, as follows.
![]() (27)
(27)
![]() (28)
(28)
Combining ![]() with Equations (27) and (28), the displacement at ini-
with Equations (27) and (28), the displacement at ini-
tial point uj and at end point us needed by the catastrophe instability of perilous rock are achieved followings, respectively.
![]() (29)
(29)
![]() (30)
(30)
According to the integral on x in Equation (19), the potential function for catastrophe model is expressed as,
![]() (31)
(31)
where, c2 is a constant and the other variables are the same as above.
From the differential ![]() of potential function, a catastrophe equation for elastic energy released by x, jumping from the inferior leaf of surface to superior leaf, is derived.
of potential function, a catastrophe equation for elastic energy released by x, jumping from the inferior leaf of surface to superior leaf, is derived.
![]() (32)
(32)
Based on Equations (27) to (32), then
![]() (33)
(33)
It indicates that the total potential energy after instability of perilous rock is lower than the one before its instability, thus, Equation (15) is coordinated, as follows.
![]() (34)
(34)
At the transient of catastrophe instability for perilous rock, the elastic energy can be transferred into the kinetic energy by the equation as follows,
![]() (35)
(35)
For the massive perilous rock, its failure velocity is fit to take the average velocity. However, for the columnar and platy perilous rock like W2 of Wangxia perilous rock, it possesses qualities such as: height is much larger than thickness. At the transient failure, it is difficult to reach the displacement triggering rupture of the whole perilous rock, actually, the end area of dominant fissure of perilous rock firstly obtains the released energy to reach the elastic-impulsive velocity as the velocity for top of perilous rock is zero. The elastic-impulsive velocity of failure and acceleration for the bottom of perilous rock are deduced as followings, respectively.
![]() (36)
(36)
![]() (37)
(37)
where, vb is the departure violent-slide velocity for the bottom of perilous rock (m/s); ab is the elastic-impulsive (or transient) acceleration for the bottom failure of perilous rock (m/s).
For the top of Wangxia perilous rock, the natural bulk density of the chert limestone is 26.3 kN/m3, the saturation bulk density is 27.0 kN/m3, the cohesion is 700 kPa and the internal friction angle is 45.38˚. For its base, the natural bulk density of carbonaceous shale is 22.5 kN/m3, the saturation bulk density is 23.0 kN/m3, the cohesion is 200 kPa and the internal friction angle is 29.9˚. For the locked patch of dominant fissure in W2 perilous rock, the dip angle α is 42˚, the thickness h is 0.3 m, the weight mg unit width perilous rock is 23198 kN. For the elastic segment of dominant fissure, the cohesion is 60 kPa, the internal friction angle is 19.38˚, shear modulus G2 is 18.71 Gpa, parameter β of water retaining strength is 0.79, and parameter S1 is 8.5 m. For the strain-softening segment, the cohesion is 30 kPa, the internal friction angle is 13.2˚, shear modulus G2 is 4.23 Gpa, parameter β of water retaining strength is 0.29, parameter S1 is 4.1 m, and u0 is 0.15 × 10−2 m. Moreover, the saturation Sr for elastic segment is 86% and about 84% for strain-softening segment.
Based on the related parameters above presentation, some intermediate variable are achived as follows.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]()
It indicates that the dominant fissure of perilous rock is at the accelerated creep state. The energy release quantity ΔE at this moment is 7920 kJ, hereby, the transient acceleration a for the failure of the perilous rock is
531.4 m
/s2 and the average elastic and impulsive velocity v is 2.608 m/s. According to that, it can be deduced that the elastic-impulsive velocity at the base of the W2 of Wangxia perilous rock is about 5.2 m/s. Therefore, for the fracture moment of the W2 of Wangxia perilous rock, characteristics with rotation and translation are visualized obviously due to the great speed difference between the top and the base of the perilous rock block. However, in virtue of the anti-slide at the base of the W2 of Wangxia perilous rock and the friction effect produced by the top of perilous rock back against matrix surface, the W2 stops on the matrix ultimately (Figure 2) and it coincides with the fact.
5. Conclusions
Firstly, the Wangxia perilous rock in Wu Gorge of the Yangtze River, China, is composed of siliceous limestone and argillaceous limestone, and includes two block marking in W1 and W2. W1 is an isolatedpillar and W2 is in clintheriform. The linking patch of dominant fissure in W2 is composed by moniliform solution funnels at its back, and the locked patch of dominant fissure at the base of perilous rock is composed by two parts. Where the upper segment shows the same lithology with perilous rock and it can be simplified as elastic medium, for the lower segment, it is composed by argillaceous shale and mudstone and can be simplified as strain-softening medium. The failure mode of Wangxia perilous rock manifests as retroverted sliding failure.
Secondly, according to the geological model of W2 of Wangxia perilous rock, its mechanical model is established. By using the weakening-water function, the constitutive curves for the locked patch of dominant fissure with two kinds of medium materials has been proposed.
Thirdly, based on energy principle, the cusp catastrophe model for the failure of perilous rock is built and formulas for the transient elastic and impulsive acceleration and the elastic-impulsive velocity of perilous rock catastrophe failure have been established.
Fourthly, by the calculation, the elastic-impulsive acceleration for the catastrophe failure of W2 of Wangxia perilous rock is
531.4 m
/s2, the average elastic and impulsive velocity is 2.608 m/s. Further, it deduces that the elastic-impulsive velocity at the base of perilous rock is about 5.2 m/s. For the transient failure of perilous rock, there is a great speed difference between the top and the base of W2 of Wangxia perilous rock, which impels perilous rock to be retroverted sliding failure and it coincides with the fact.
Acknowledgements
This study in the paper was funded by The National Natural Science Foundation of China (No. 11272185, 51678097 and 51378521), and special fund of the innovation team for Geological Disasters Mitigation along Highways & Shipping Lanes in Western China (CXTDG201602012). The authors are grateful for Prof. Xian Xue-fu, academician of Chinese academy of engineering, and Prof. Li Ji-jun, academician of
Chinese
Academy
of Sciences.