A New Approach for Solving Linear Fractional Programming Problems with Duality Concept

Farhana Ahmed Simi¹, Md. Shahjalal Talukder²

¹Department of Mathematics, Dhaka University, Dhaka, Bangladesh.
²Department of Natural Sciences, Daffodil International University, Dhaka, Bangladesh.

DOI: 10.4236/ojop.2017.61001                

Abstract

Most of the current methods for solving linear fractional programming (LFP) problems depend on the simplex type method. In this paper, we present a new approach for solving linear fractional programming problem in which the objective function is a linear fractional function, while constraint functions are in the form of linear inequalities. This approach does not depend on the simplex type method. Here first we transform this LFP problem into linear programming (LP) problem and hence solve this problem algebraically using the concept of duality. Two simple examples to illustrate our algorithm are given. And also we compare this approach with other available methods for solving LFP problems.

Keywords

Linear Fractional Programming, Linear Programming, Duality

1. Introduction

The linear fractional programming (LFP) problem has attracted the interest of many researches due to its application in many important fields such as production planning, financial and corporate planning, health care and hospital planning.

Several methods were suggested for solving LFP problem such as the variable transformation method introduced by Charnes and Cooper [1] and the updated objective function method introduced by Bitran and Novaes [2] . The first method transforms the LFP problem into an equivalent linear programming problem and uses the variable transformation 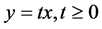in such a way that where is a specified number and transform LFP to an LP problem. And the second method solves a sequence of linear programming pro- blems depending on updating the local gradient of the fractional objective function at successive points. But to solve this sequence of problems, sometimes may need much iteration. Also some aspects concerning duality and sensitivity analysis in linear fractional program were discussed by Bitran and Magnant [3] and Singh [4] , in his paper made a useful study about the optimality condition in fractional programming. Assuming the positivity of denominator of the objective function of LFP over the feasible region, Swarup [5] extended the well- known simplex method to solve the LFP. This process cannot continue infinitely, since there is only a finite number of basis and in non-degenerate case, no basis can ever be repeated, since F is increased at every step and the same basis cannot yield two different values of F. While at the same time the maximum value of the objective function occurs at of the basic feasible solution. Recently, Tantawy [6] has suggested a feasible direction approach and the main idea behind this method for solving LFP problems is to move through the feasible region via a sequence of points in the direction that improves the objective function. Tantawy [7] also proposed a duality approach to solve a linear fractional programming problem. Tantawy [8] develops another technique for solving LFP which can be used for sensitivity analysis. Effati and Pakdaman [9] propose a method for solving interval-valued linear fractional programming problem. A method for solving multi objective linear plus linear fractional programming problem based on Taylor series approximation is proposed by Pramanik et al. [10] . Tantawy and Sallam [11] also propose a new method for solving linear programming problems.

In this paper, our main intent is to develop an approach for solving linear fractional programming problem which does not depend on the simplex type method because method based on vertex information may have difficulties as the problem size increases; this method may prove to be less sensitive to problem size. In this paper, first of all, a linear fractional programming problem is transformed into linear programming problem by choosing an initial feasible point and hence solves this problem algebraically using the concept of duality.

2. Definition and Method of Solving LFP

A linear fractional programming problem occurs when a linear fractional function is to be maximized and the problem can be formulated mathematically as follows:

Maximize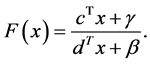

Subject to,

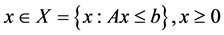(1)

where c, d and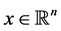, A is an 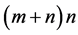matrix, 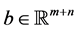and and are scalars.

We point out that the nonnegative conditions are included in the set of constraints and that has to be satisfied over the compact set X.

To transform the LFP problem into LP problem, we choose a feasible point 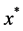of the compact set X. Then

(2)

is a given constant vector computed at a given feasible point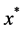. Thus the level curve of objective function for (1) can be written as

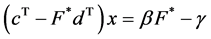
Hence the linear programming problem is as follows:

Maximize

Subject to,

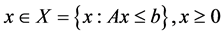(3)

Proposition

If 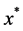solves the LFP problem (1) with objective function values then solves the LP problem defined by (3) with objective function value.

Now rewrite the LP problem (3) in the form

Maximize

Subject to,

(4)

where, is a matrix whose row is represented by and, is a matrix, we point out that the nonnegative conditions are included in the set of constraints.

Now consider the dual problem for the linear program (4) in the form

Minimize

Subject to,

(5)

Since the set of constraints of this dual problem is written in the matrix form hence we can multiply both side by a matrix, where and the columns of the matrix constitute the bases of.

Thus this implies

, and. (6)

If we define matrix of nonnegative entries such that , then (6) can be written as

(7)

where and, Equation (7) will play an important role for finding the optimal solution of the LP problem (4). Using the Equation (7) the equivalent LP problem of (5) can be written as

Minimize

Subject to,

(8)

with, the linear programming (8) has the dual programming problem in just one unknown Z in the form.

Maximize

Subject to,

(9)

Note: The set of constraints of the above linear programming problem will give the maximum value and also will define only one active constraint for this optimal value. We have to note that from the complementary slackness theorem the corresponding dual variable will be positive and the remaining dual variables will be zeros for the corresponding non active constraints.

3. Algorithm for Solving LFP Problems

The method for solving LFP problems summarize as follows:

Ÿ Step 1: Select a feasible point and using Equation (2) to compute.

Ÿ Step 2: Find the level curve of objective function

Hence find the LP problem (2) which can be rewritten as (3).

Ÿ Step 3: Compute, and the matrix as the bases of .

Ÿ Step 4: Find the matrix of nonnegative entries such that and hence compute.

Ÿ Step 5: Find the LP problem (8) and dual of this LP (9). Use the LP (9) to find the optimal value and also determine the corresponding active constraints and use the constraint of (8) to compute.

Ÿ Step 6: Find the dual variables, for each positive variable find the corresponding active set of constraint of the matrix.

Ÿ Step 7: Solve a system of linear equations for these set of active constraints (a subset from a constraints) to get the optimal solution of LP problem (4) and hence for the LFP problem (1).

4. Computational Process

Choose in such a way that

The level curve is.

Then or;

;

Find such that.

Compute;

Formulate, Maximize

Subject to,

Find and corresponding active constraint and compute for ;

Then; hence find from corresponding active constraints satisfied by positive;

Compute and.

5. Numerical Examples

Here we illustrate two examples to demonstrate our method.

Example 1: Consider the linear fractional programming (LFP) problem

Maximize

Subject to,

Solution:

Step 1: Let, then and hence we have

Step 2: Therefore we have the following LP problem

Maximize

Subject to,

Dual problem for this LP problem is

Minimize

Subject to,

Step 3: Compute.

And the matrix.

Step 4: Compute nonnegative matrix such that,

.

Also compute

Step 5: We get the LP problem of the form

Maximize

Subject to,

For this LP problem we get that the first constraint is the only active constraint and this active constraint shows that the maximum optimal value is

. Corresponding this active constraint of (8), we get the dual variables

Step 6: Compute with objective value.

This indicates that in the original set of constraints the first and the second constraints are the only active constraints.

Step 7: Solve the system of linear equations

We get the optimal solution of the LP problem with objective value.

Finally we get our desired optimal solution of the given LFP problem is with the optimal value.

Example 2: Consider the linear fractional programming (LFP) problem

Maximize

Subject to,

Solution:

Step 1: Let, then and hence we have

Step 2: Therefore we have the following LP problem

Maximize

Subject to,

Dual problem for this LP problem is

Minimize

Subject to,

Step 3: Compute.

And the matrix.

Step 4: Compute nonnegative matrix such that,

.

Also compute

Step 5: We get the LP problem of the form

Maximize

Subject to,

For this LP problem we get that the first constraint is the only active constraint and this active constraint shows that the maximum optimal value is. Corresponding to this active constraint of (8), we get the dual variables

Step 6: Compute with objective value.

This indicates that in the original set of constraints the first and the third constraints are the only active constraints.

Step 7: Solve the system of linear equations

We get the optimal solution of the LP problem with objective value.

Finally we get our desired optimal solution of the given LFP problem is with the optimal value.

Table 1. Results of existing and our methods for Example 1 and Example 2.

Now different methods can be compared with our method and all the methods give the same results for Example 1 and Example 2. Table 1 shows the results of number of iterations that are required for our method and the existing methods for these Examples.

6. Comparison

In this Section, we find that our method is better than any other available method. The reason can be given as follows:

§ Any type of LFP problem can be solved by this method.

§ The LFP problem can be transformed into LP problem easily with initial guess.

§ In this method, problems are solved by algebraically with duality concept. So that it’s computational steps are so easy from other methods.

§ The final result converges quickly in this method.

§ In some cases of numerator and denominator, other existing methods are failed but our method is able to solve any kind of problem easily.

7. Conclusion

In this paper, we give an approach for solving linear fractional programming problems. The proposed method differs from the earlier methods as it is based upon solving the problem algebraically using the concept of duality. This method does not depend on the simplex type method which searches along the boundary from one feasible vertex to an adjacent vertex until the optimal solution is found. In some certain problems, the number of vertices is quite large, hence the simplex method would be prohibitively expensive in computer time if any substantial fraction of the vertices had to be evaluated. But our proposed method appears simple to solve any linear fractional programming problem of any size.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Charnes, A. and Cooper, W.W. (1962) Programming with Fractional Functions. Naval Research Logistic Quarterly, 9, 181-186. https://doi.org/10.1002/nav.3800090303
[2]	Bitran, G.R. and Novaes, A.G. (1973) Linear Programming with a Fractional Objective Functions. Operations Research, 21, 22-29. https://doi.org/10.1287/opre.21.1.22
[3]	Bitran, G.R. and Magnanti, T.L. (1976) Duality and Sensitivity Analysis with Fractional Objective Function. Journal of Operation Research, 24, 675-699. https://doi.org/10.1287/opre.24.4.675
[4]	Sing, H.C. (1981) Optimality Condition in Fractional Programming. Journal of Optimization Theory and Applications, 33, 287-294. https://doi.org/10.1007/BF00935552
[5]	Swarup, K. (1964) Linear Fractional Programming. Operation Research, 13, 1029-1036. https://doi.org/10.1287/opre.13.6.1029
[6]	Tantawy, S.F. (2008) A New Procedure for Solving Linear Fractional Programming Problems. Mathematical and Computer Modelling, 48, 969-973. https://doi.org/10.1016/j.mcm.2007.12.007
[7]	Tantawy, S.F. (2014) A New Concept of Duality for Linear Fractional Programming Problems. International Journal of Engineering and Innovative Technology, 3, 147-149.
[8]	Effati, S. and Pakdaman, M. (2012) Solving the Interval-Valued Linear Fractional Programming Problem. American Journal of Computational Mathematics, 5, 51-55. https://doi.org/10.4236/ajcm.2012.21006
[9]	Pramanik, S., Dey, P.P. and Giri, B.C. (2011) Multi-Objective Linear Plus Linear Fractional Programming Problem Based on Taylor Series Approximation. International Journal of Computer Applications, 32, 61-68.
[10]	Tantawy, S.F. (2008) An Iterative Method for Solving Linear Fractional Programming (LFP) Problem with Sensitivity Analysis. Mathematical and Computational Mathematics, 13, 147-151.
[11]	Tantawy, S.F. and Sallam, R.H. (2013) A New Method for Solving Linear Fractional Programming Problems. International Journal of Recent Scientific Research, 4, 623-625.