On Local Existence and Blow-Up of Solutions for Nonlinear Wave Equations of Higher-Order Kirchhoff Type with Strong Dissipation ()
1. Introduction
In this paper, we are concerned with local existence and blow-up of the solution for nonlinear wave equations of Higher-order Kirchhoff type with strong dissi- pation:
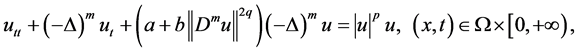 (1.1)
(1.1)
 (1.2)
(1.2)
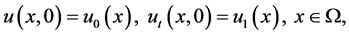 (1.3)
(1.3)
where 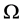 is a bounded domain in
is a bounded domain in  with the smooth boundary
with the smooth boundary  and
and 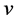 is the unit outward normal on
is the unit outward normal on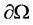 . Moreover,
. Moreover, 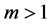 is an integer constant, and
is an integer constant, and ,
, 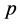 ,
, 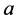 and
and 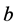 are some constants such that
are some constants such that![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . We call Equation (1.1) a non-degenerate equation when
. We call Equation (1.1) a non-degenerate equation when ![]() and
and![]() , and a degenerate one when
, and a degenerate one when ![]() and
and![]() . In the case of
. In the case of ![]() and
and![]() , Equation (1.1) is usual semilinear wave equations.
, Equation (1.1) is usual semilinear wave equations.
It is known that Kirchhoff [1] first investigated the following nonlinear vib- ration of an elastic string for![]() :
:
![]() (1.4)
(1.4)
where ![]() is the lateral displacement at the space coordinate
is the lateral displacement at the space coordinate ![]() and the time
and the time![]() ;
;![]() : the mass density;
: the mass density;![]() : the cross-section area;
: the cross-section area;![]() : the length;
: the length;![]() : the Young modulus;
: the Young modulus;![]() : the initial axial tension;
: the initial axial tension;![]() : the resistance modulus; and
: the resistance modulus; and![]() : the external force.
: the external force.
When![]() , the Equation (1.1) becomes a nonlinear wave equation:
, the Equation (1.1) becomes a nonlinear wave equation:
![]() (1.5)
(1.5)
![]() (1.6)
(1.6)
![]() (1.7)
(1.7)
It has been extensively studied and several results concerning existence and blowing-up have been established [2] [3] [4] .
When![]() , the Equation (1.1) becomes the following Kirchhoff equation with Lipschitz type continuous coefficient and strong damping:
, the Equation (1.1) becomes the following Kirchhoff equation with Lipschitz type continuous coefficient and strong damping:
![]() (1.8)
(1.8)
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
where ![]() is a bounded domain with a smooth boundary
is a bounded domain with a smooth boundary![]() . p > 2 and
. p > 2 and ![]() is a positive local Lipschitz function. Here,
is a positive local Lipschitz function. Here,![]()
![]() . It has been studied and several results concerning existence and blowing-up have been established [5] .
. It has been studied and several results concerning existence and blowing-up have been established [5] .
When![]() , the Equation (1.1) becomes the following Kirchhoff equation:
, the Equation (1.1) becomes the following Kirchhoff equation:
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
![]() (1.13)
(1.13)
where ![]() is a bounded domain in
is a bounded domain in ![]() with the smooth boundary
with the smooth boundary ![]() and
and ![]() is the unit outward normal on
is the unit outward normal on![]() . Moreover,
. Moreover, ![]() ,
, ![]() ,
, ![]() and
and ![]() are some constants such that
are some constants such that![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . It has been studied and several results concerning existence and blowing-up have been established [6] .
. It has been studied and several results concerning existence and blowing-up have been established [6] .
When![]() , reference [7] has considered global existence and decay esti- mates for nonlinear Kirchhoff-type equation:
, reference [7] has considered global existence and decay esti- mates for nonlinear Kirchhoff-type equation:
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
![]() (1.17)
(1.17)
where ![]() is a bounded domain of
is a bounded domain of ![]() with smooth boundary
with smooth boundary ![]() such that
such that ![]() and
and ![]() have positive measures, and
have positive measures, and ![]() is the unit
is the unit
outward normal on![]() , and
, and ![]() is the outward normal derivative on
is the outward normal derivative on![]() .
.
The content of this paper is organized as follows. In Section 2, we give some lemmas. In Section 3, we prove the existence and uniqueness of the local solution by the Banach contraction mapping principle. In Section 4, we study the blow-up properties of solution for positive and negative initial energy and esti- mate for blow-up time ![]() by lemma of [9] .
by lemma of [9] .
2. Preliminaries
In this section, we introduce material needed in the proof our main result. We use the standard Lebesgue space ![]() and Sobolev space
and Sobolev space ![]() with their usual scalar products and norms. Meanwhile we define
with their usual scalar products and norms. Meanwhile we define
![]() and introduce the following
and introduce the following
abbreviations: ![]() for any real number
for any real number![]() .
.
Lemma 2.1 (Sobolev-Poincaré inequality [8] ) Let ![]() be a number with
be a number with
![]() and
and![]() . Then there is a constant
. Then there is a constant ![]()
depending on ![]() and
and ![]() such that
such that
![]() (2.1)
(2.1)
Lemma 2.2 [9] Suppose that ![]() and
and ![]() is a nonnegative
is a nonnegative ![]() function such that
function such that
![]() (2.2)
(2.2)
If
![]() (2.3)
(2.3)
then we have![]() . Here,
. Here, ![]() is a constant and
is a constant and
![]() the smallest positive root of the equation
the smallest positive root of the equation
![]()
Lemma 2.3 [9] If ![]() is a non-increasing function on
is a non-increasing function on ![]() such that
such that
![]() (2.4)
(2.4)
where![]() . Then there exists a finite time
. Then there exists a finite time ![]() such that
such that
![]() .
.
Moreover, for the case that ![]() an upper bound of
an upper bound of ![]() is
is ![]()
If![]() , we have
, we have ![]()
If![]() , we have
, we have ![]() or
or ![]()
3. Local Existence of Solution
Theorem 3.1 Suppose that ![]() (
(![]() if
if![]() ) and
) and
for any given![]() , then there exists
, then there exists ![]() such that the problem (1.1)-(1.3) has a unique local solution satisying
such that the problem (1.1)-(1.3) has a unique local solution satisying
![]() (3.1)
(3.1)
Proof. We proof the theorem by Banach contraction mapping principle. For ![]() and
and![]() , we define the following two-parameter space of solutions:
, we define the following two-parameter space of solutions:
![]() (3.2)
(3.2)
where![]() . Then
. Then ![]() is a complete metric space with the distance
is a complete metric space with the distance
![]() (3.3)
(3.3)
We define the non-linear mapping ![]() in the following way. For
in the following way. For ![]()
![]() is the unique solution of the following equation:
is the unique solution of the following equation:
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
We shall show that there exist ![]() and
and ![]() such that
such that
1) ![]() maps
maps ![]() into itself;
into itself;
2) ![]() is a contraction mapping with respect to the metric
is a contraction mapping with respect to the metric![]() .
.
First, we shall check (i). Multiplying Equation (3.4) by![]() , and
, and
integrating it over![]() , we have
, we have
![]() (3.7)
(3.7)
where![]() .
.
To proceed the estimation,we observe that for![]() . By Lemma 2.1, we have
. By Lemma 2.1, we have
![]() (3.8)
(3.8)
Because of ![]() (
(![]() if
if![]() ), then
), then
![]() (3.9)
(3.9)
Since ![]() by the Young inequality, we see that
by the Young inequality, we see that
![]() (3.10)
(3.10)
Combining these inequalities, we get
![]() (3.11)
(3.11)
Therefore, by the Gronwall inequality, we obtain
![]() (3.12)
(3.12)
where ![]()
and
![]() (3.13)
(3.13)
So, for all![]() , we obtain
, we obtain
![]() (3.14)
(3.14)
Therefore, in order that the map ![]() verifies 1), it will be enough that the parameters
verifies 1), it will be enough that the parameters ![]() and
and ![]() satisfy
satisfy
![]() (3.15)
(3.15)
Moreover, it follows from (3.14) that ![]() and
and![]() . It implies
. It implies
![]() (3.16)
(3.16)
Next, we prove 2). Suppose that (3.15) holds. We take![]() , let
, let![]() , and set
, and set![]() . Then
. Then ![]() satisfies
satisfies
![]() (3.17)
(3.17)
![]() (3.18)
(3.18)
![]() (3.19)
(3.19)
![]() (3.20)
(3.20)
Multiplying (3.17-3.18) by ![]() and integrating it over
and integrating it over ![]() and using Green’s formula, we have
and using Green’s formula, we have
![]() (3.21)
(3.21)
To proceed the estimation, by Lemma 2.1 observe that
![]() (3.22)
(3.22)
![]() (3.23)
(3.23)
where![]() .
.
![]() (3.24)
(3.24)
Substituting (3.22)-(3.24) into (3.21), we obtain
![]() (3.25)
(3.25)
According to the same method, Multiplying (3.17-3.18) by ![]() and inte- grating it over
and inte- grating it over![]() , we get
, we get
![]() (3.26)
(3.26)
Taking (3.25) ![]() (3.26) and by (3.10), it follows that
(3.26) and by (3.10), it follows that
![]() (3.27)
(3.27)
where ![]()
and![]() .
.
Applying the Gronwall inequality, we have
![]() (3.28)
(3.28)
So, by (3.10) we have
![]() (3.29)
(3.29)
where![]() . If
. If![]() , we can see
, we can see ![]() is a contraction mapping. Finally, we choose suitable
is a contraction mapping. Finally, we choose suitable ![]() is suffi- ciently large and
is suffi- ciently large and ![]() is sufficiently small, such that 1) and 2) hold. By applying Banach fixed point theorem, we obtain the local existence.
is sufficiently small, such that 1) and 2) hold. By applying Banach fixed point theorem, we obtain the local existence.
4. Blow-Up of Solution
In this section, we shall discuss the blow-up properties for the problem (1.1)- (1.3). For this purpose, we give the following definition and lemmas.
Now, we define the energy function of the solution ![]() of (1.1)-(1.3) by
of (1.1)-(1.3) by
![]() (4.1)
(4.1)
Then, we have
![]() (4.2)
(4.2)
where ![]()
Definition 4.1 A solution ![]() of (1.1)-(1.3) is called a blow-up solution, if there exists a finite time
of (1.1)-(1.3) is called a blow-up solution, if there exists a finite time ![]() such that
such that
![]() (4.3)
(4.3)
For the next lemma, we define
![]() (4.4)
(4.4)
Lemma 4.1 Suppose that ![]() (
(![]() if
if![]() ) and
) and
![]() hold. Then we have the following results, which are
hold. Then we have the following results, which are
1)![]() , for t ≥ 0;
, for t ≥ 0;
2) If![]() , we get
, we get ![]() for
for![]() , where
, where
![]() ;
;
3) If ![]() and if
and if ![]() hold, then we
hold, then we
have ![]() for
for![]() ;
;
4) If ![]() and
and
![]()
hold, then we get ![]() for
for![]() .
.
Proof. Step 1: From (4.4), we obtain
![]() (4.5)
(4.5)
and
![]() (4.6)
(4.6)
From the above equation and the energy identity and![]() , we obtain
, we obtain
![]()
(4.7)
Therefore, we obtain 1).
Step 2: If![]() , then by (i), we have
, then by (i), we have
![]() (4.8)
(4.8)
Integrating (4.8) over![]() , we have that
, we have that
![]() (4.9)
(4.9)
Thus, we get ![]() for
for![]() , where
, where
![]() .
.
So, 2) has been proved.
Step 3: If![]() , then for
, then for ![]() we have
we have
![]() (4.10)
(4.10)
Integrating (4.10) over![]() , we have that
, we have that
![]() (4.11)
(4.11)
And because of![]() , then we get
, then we get
![]() .
.
Thus, 3) has been proved.
Step 4: For the case that![]() , we first note that
, we first note that
![]() (4.12)
(4.12)
By using Hölder inequality, we have
![]() (4.13)
(4.13)
So
![]() (4.14)
(4.14)
Thus, we have
![]() (4.15)
(4.15)
where ![]()
Set
![]() (4.16)
(4.16)
Then ![]() satisfies (2.2). By conditions
satisfies (2.2). By conditions
![]()
and Lemma 2.2, then ![]() for
for![]() .
.
Lemma 4.2 Suppose that ![]() (
(![]() if
if![]() ) and
) and
![]() hold and that eigher one of the following conditions is satisfied:
hold and that eigher one of the following conditions is satisfied:
1)![]() ;
;
2) ![]() and
and![]() ;
;
3) ![]() and
and
![]()
hold.
Then, there exists![]() , such that
, such that ![]() for
for![]() .
.
Proof. By Lemma 4.1, ![]() in case (i) and
in case (i) and ![]() in case 2) and 3).
in case 2) and 3).
Theorem 4.1 Suppose that ![]() (
(![]() if
if![]() ) and
) and
![]() hold and that eigher one of the following conditions is satisfied:
hold and that eigher one of the following conditions is satisfied:
1)![]() ;
;
2) ![]() and
and![]() ;
;
3) ![]() and
and
![]()
hold.
Then the solution ![]() blow up at finite
blow up at finite![]() . And
. And ![]() can be estimated by (4.26)-(4.29), respectively, according to the sign of
can be estimated by (4.26)-(4.29), respectively, according to the sign of![]() .
.
Proof. Let
![]() (4.17)
(4.17)
where ![]() is some certain constant which will be chosen later. Then we get
is some certain constant which will be chosen later. Then we get
![]() (4.18)
(4.18)
and
![]() (4.19)
(4.19)
where ![]()
By the Hölder inequality, we obtain
![]() (4.20)
(4.20)
where![]() .
.
By 1) of Lemma 4.1, we get
![]() (4.21)
(4.21)
Then, we obtain
![]() (4.22)
(4.22)
Therefore, we get
![]() (4.23)
(4.23)
Note that by Lemma 4.2, ![]() Multiplying (4.23) by
Multiplying (4.23) by ![]() and integrating it from
and integrating it from ![]() to
to![]() , we have
, we have
![]() (4.24)
(4.24)
where![]() , and
, and
![]() .
.
When ![]() and
and![]() , we obviously have
, we obviously have![]() . When
. When![]() ,
,
we also have ![]() by condition
by condition![]() .
.
Then by Lemma 2.3, there exists a finite time ![]() such that
such that ![]()
and the upper bounds of ![]() are estimated respectively according to the sign of
are estimated respectively according to the sign of![]() . This will imply that
. This will imply that
![]() (4.25)
(4.25)
Next, ![]() are estimated respectively according to the sign of
are estimated respectively according to the sign of ![]() and Lemma 2.3.
and Lemma 2.3.
In case 1), we have
![]() (4.26)
(4.26)
Furthermore, if![]() , then we have
, then we have
![]() (4.27)
(4.27)
In case 2), we get
![]() (4.28)
(4.28)
In case 3), we obtain
![]() (4.29)
(4.29)
where![]() . Note that in case 1),
. Note that in case 1), ![]() is given Lemma 4.1, and in
is given Lemma 4.1, and in
case 2) and case 3)![]() .
.
Remark 4.1 [10] The choice of ![]() in (4.17) is possible under some conditions.
in (4.17) is possible under some conditions.
1) In the case![]() , we can choose
, we can choose![]() . In particular, we choose
. In particular, we choose![]() , then we get
, then we get![]() .
.
2) In the case![]() , we can choose
, we can choose ![]() as in 1) if
as in 1) if ![]() or
or ![]() if
if![]() .
.
3) For the case![]() . Under the condition
. Under the condition![]() ,
,
here![]() ,
, ![]() ,
,
if![]() ,
, ![]() is chosen to satisfy
is chosen to satisfy![]() , where
, where![]() ,
, ![]() Therefore, we have
Therefore, we have
![]() .
.
5. Conclusion
In this paper, we prove that nonlinear wave equations of higher-order Kirchhoff Type with Strong Dissipation exist unique local solution on
![]() . Then, we establish three blow-up results for certain solutions in the case 1):
. Then, we establish three blow-up results for certain solutions in the case 1):![]() , in the case 2):
, in the case 2): ![]() and in the case 3):
and in the case 3):![]() . At last, we consider that the estimation of the upper bounds of the blow-up time
. At last, we consider that the estimation of the upper bounds of the blow-up time ![]() is given for deferent initial energy.
is given for deferent initial energy.
Acknowledgements
The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper.
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11561076.