Coherent Application of a Contact Structure to Formulate Classical Non-Equilibrium Thermodynamics ()
1. Introduction
The main objective of this paper is to derive a mathematical framework for macroscopic non-equilibrium thermodynamics, which is not based on some kind of an (implicit) equilibrium assumption. Instead it will be shown, that the equilibrium conditions are “contained” in the proposed framework by applying an additional constraint. There are two key components in this innovative derivation: 1) a generalization of Gibbs fundamental relation for non-equilibrium thermodynamics that is based on the dissipation of energy and 2) a unique formulation of the second law of thermodynamics, including a mathematical proper derivation of non-equilibrium entropy as a thermodynamic state function. This paper presents the mathematical framework of Classical Non-Equilibrium Thermodynamics (CNET) based on a harmonious integration of mathematics and physics.
In his monumental work “On the Equilibrium of Heterogeneous Substances” [1] Josiah Willard Gibbs (1839-1903) postulates a relation that is fundamental for thermodynamics, viz.
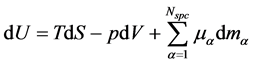 . (1)
. (1)
Gibbs postulates this relation for a mixture of  non-reacting, chemical species in a closed system, which is in a thermodynamic equilibrium state. Often this relation is derived by a simple elimination of the reversible heat flow from both laws of thermodynamics [2] - [7] or it is applied in non-equilibrium states by using the local equilibrium hypothesis [8] . In this paper, only a state space for non-equilibrium thermodynamics will be postulated and the corresponding generalization of the fundamental relation will be derived. This paper will be restricted to closed, single component systems, but a proposition to include the physical phenomena of open systems with chemical reactions can be found in [9] .
non-reacting, chemical species in a closed system, which is in a thermodynamic equilibrium state. Often this relation is derived by a simple elimination of the reversible heat flow from both laws of thermodynamics [2] - [7] or it is applied in non-equilibrium states by using the local equilibrium hypothesis [8] . In this paper, only a state space for non-equilibrium thermodynamics will be postulated and the corresponding generalization of the fundamental relation will be derived. This paper will be restricted to closed, single component systems, but a proposition to include the physical phenomena of open systems with chemical reactions can be found in [9] .
Based on the original work of Rudolf Clausius (1822-1888), the macroscopic entropy of systems in thermodynamic equilibrium is often defined as the quotient of heat flow and temperature. For non-equilibrium processes this definition is then simply extended to an inequality (e.g. Clausius inequality [6] ) or an additional term is included in the definition of macroscopic entropy [10] . The major drawback of these approaches is, that it is not obvious that entropy is also a state function in non-equilibrium thermodynamics. It is often reasoned, that the non-equilibrium entropy has to be a thermodynamic state function. This paper presents a unique postulate for the second law of thermodynamics, which does not explicitly include the concept of entropy. Based on a mathematical property of this postulate, the non-equilibrium entropy will be derived with the appropriate mathematical structure of a thermodynamic state function. This paper is confined to the thermodynamic state space, there is no reference to temporal or spatial coordinates.
Section 2 starts with the introduction of a thermodynamic state and defines a corresponding state function. The mathematical machinery of contact geometry is used to postulate the so-called non-equilibrium state space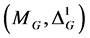 . Darboux’s theorem can be derived for a contact structure, which possesses the mathematical structure of the Gibbs fundamental relation in thermodynamics (viz. Equation (1)). In the third section the first law of thermodynamics is postulated in such a way, that the internal energy is a state function that complies with the appropriate definition. The next step is to postulate a unique formulation for the second law of thermodynamics and the complying derivation of non-equili- brium entropy. Both sections are combined in Section 4 to identify the thermodynamic potential as Gibbs free energy and to identify the pairs of conjugated coordinates in Darboux’s theorem. With this identification, a generalized Gibbs fundamental relation for non-equilibrium thermodynamics is derived, which includes sufficient additional degrees of freedom to model non-equilibrium phenomena. The postulate for a thermodynamic equilibrium is postponed until the final section of this paper. It will be shown how the equilibrium constraint reduces Gibbs fundamental relation to a Pfaffian equation, which is the basis for the derivation of the so-called Maxwell relations in thermodynamics [3] [5] [6] [7] .
. Darboux’s theorem can be derived for a contact structure, which possesses the mathematical structure of the Gibbs fundamental relation in thermodynamics (viz. Equation (1)). In the third section the first law of thermodynamics is postulated in such a way, that the internal energy is a state function that complies with the appropriate definition. The next step is to postulate a unique formulation for the second law of thermodynamics and the complying derivation of non-equili- brium entropy. Both sections are combined in Section 4 to identify the thermodynamic potential as Gibbs free energy and to identify the pairs of conjugated coordinates in Darboux’s theorem. With this identification, a generalized Gibbs fundamental relation for non-equilibrium thermodynamics is derived, which includes sufficient additional degrees of freedom to model non-equilibrium phenomena. The postulate for a thermodynamic equilibrium is postponed until the final section of this paper. It will be shown how the equilibrium constraint reduces Gibbs fundamental relation to a Pfaffian equation, which is the basis for the derivation of the so-called Maxwell relations in thermodynamics [3] [5] [6] [7] .
2. Non-Equilibrium State Space
A powerful feature of phenomenological thermodynamics is its capability to make statements about the macroscopic state of a system without detailed knowledge of its microscopic details. This feature is based on the phenomenological observation, that a finite number of macroscopic properties is required to completely describe the thermodynamics of a system. Non-equilibrium thermodynamics will be described in a separate state space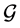 , which is based on statistical averages of the phase space in statistical mechanics.
, which is based on statistical averages of the phase space in statistical mechanics.
A thermodynamic system consists of  molecules, where each individual molecule
molecules, where each individual molecule 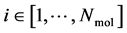 has a position
has a position 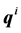 and a momentum
and a momentum . The complete set of these
. The complete set of these  positions and
positions and 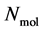 momenta form the so-called microscopic state of the system. The number of degrees of freedom in this system is, in the case of a 3-dimensional spatial space, equal to
momenta form the so-called microscopic state of the system. The number of degrees of freedom in this system is, in the case of a 3-dimensional spatial space, equal to  (where
(where ). A macroscopic state is a statistical ensemble of this huge amount of microscopic information, where there is a probability distribution over all compatible microscopic states of the system. The corresponding probability density
). A macroscopic state is a statistical ensemble of this huge amount of microscopic information, where there is a probability distribution over all compatible microscopic states of the system. The corresponding probability density  determines the probability that the system will be found in the infinitesimal phase space volume
determines the probability that the system will be found in the infinitesimal phase space volume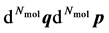 . It complies with
. It complies with
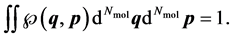 (2)
(2)
Then the statistical average of some physical observable  can be written as (e.g. see [11] [12] [13] [14] )
can be written as (e.g. see [11] [12] [13] [14] )
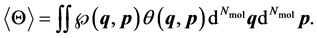 (3)
(3)
This equation defines a macroscopic property of a system, which will be applied as a coordinate for the differential manifold 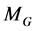 of the thermodynamic state space
of the thermodynamic state space![]() . At this point, no clear mathematical distinction will be made between the definition of the chart
. At this point, no clear mathematical distinction will be made between the definition of the chart![]() , as part of the definition of the manifold
, as part of the definition of the manifold![]() , and the set of values of the macroscopic properties
, and the set of values of the macroscopic properties![]() , which form together the thermodynamic state
, which form together the thermodynamic state![]() . Typical examples for macroscopic properties are energy
. Typical examples for macroscopic properties are energy![]() , volume
, volume![]() , number of molecules
, number of molecules ![]() or electric charge
or electric charge![]() . A set of
. A set of ![]() coordinates builds a macroscopic non-equilibrium state, viz.
coordinates builds a macroscopic non-equilibrium state, viz.![]() . Notice that there is no explicit expression for time nor for spatial distributions of macroscopic properties within the system.
. Notice that there is no explicit expression for time nor for spatial distributions of macroscopic properties within the system.
Non-equilibrium thermodynamics describes changes in a system, which depend on changes in its state ![]() due to some arbitrary process
due to some arbitrary process![]() . There are various macroscopic properties of the system that depend on the state
. There are various macroscopic properties of the system that depend on the state![]() , which requires the definition of a so-called state function
, which requires the definition of a so-called state function![]() .
.
Definition 1 [Non-equilibrium state function]. The 0-form![]() , that is generated by an exact 1-form
, that is generated by an exact 1-form![]() , is defined as a non-equilibrium state function. Hence,
, is defined as a non-equilibrium state function. Hence,
![]() (4)
(4)
In this definition symbol ![]() denotes an exterior derivative with respect to the thermodynamic coordinates
denotes an exterior derivative with respect to the thermodynamic coordinates![]() , which makes it an essential part of the definition. It describes the dependencies of the thermodynamic changes, which are given by the set
, which makes it an essential part of the definition. It describes the dependencies of the thermodynamic changes, which are given by the set ![]() of independent macroscopic properties of the system (again, there is no reference to temporal or spatial coordinates). Another important aspect of the above definition is that any non-equilibrium property can return to its initial condition after an arbitrary periodic process has concluded a complete period1.
of independent macroscopic properties of the system (again, there is no reference to temporal or spatial coordinates). Another important aspect of the above definition is that any non-equilibrium property can return to its initial condition after an arbitrary periodic process has concluded a complete period1.
The manifold ![]() is not sufficient to completely describe non-equilibrium thermodynamics. By using the mathematical framework of contact geometry, the thermodynamic space can be based on the concept of a contact structure. In 1973 Robert Hermann [15] suggested to formulate equilibrium thermodynamics based on a
is not sufficient to completely describe non-equilibrium thermodynamics. By using the mathematical framework of contact geometry, the thermodynamic space can be based on the concept of a contact structure. In 1973 Robert Hermann [15] suggested to formulate equilibrium thermodynamics based on a ![]() -dimensional differential manifold
-dimensional differential manifold ![]() and a non-de- generating contact 1-form
and a non-de- generating contact 1-form![]() . In this paper his mathematical framework will be used as the basic building block to formulate non-equilibrium thermodynamics.
. In this paper his mathematical framework will be used as the basic building block to formulate non-equilibrium thermodynamics.
Postulate 1 [Gibbs state space]. Non-equilibrium thermodynamics is specified by a ![]() -dimensional differential manifold
-dimensional differential manifold![]() , that is equipped with a non-degenerate Gibbs contact 1-form
, that is equipped with a non-degenerate Gibbs contact 1-form![]() , viz.
, viz.
![]() (5)
(5)
The Gibbs state space ![]() is defined by the contact structure
is defined by the contact structure![]() .
.
In the general context of this paper, it is very important to notice, that this postulate is neither the first law nor the second law of thermodynamics. The above postulate states that the contact structure ![]() formulates a non-equilibrium thermodynamic state space. In this paper, all thermodynamic observations will be formulated in this state space. The non-degenerate Gibbs contact 1-form
formulates a non-equilibrium thermodynamic state space. In this paper, all thermodynamic observations will be formulated in this state space. The non-degenerate Gibbs contact 1-form ![]() has two important mathematical properties (see [16] [17] ):
has two important mathematical properties (see [16] [17] ):
・ it is never equal to zero, so it is either everywhere positive or it is everywhere negative,
・ it is not completely integrable (Frobenius condition).
Both these properties play a key role in the formulation of the second law of thermodynamics in section 3. The physical interpretation of the quantity ![]() is postponed until the next section.
is postponed until the next section.
According to Darboux’s theorem (see [16] [17] [18] [19] [20] ), there is a set of canonical coordinates ![]() on the manifold
on the manifold ![]() such that the Gibbs contact 1-form
such that the Gibbs contact 1-form ![]() is specified by
is specified by
![]() (6)
(6)
(summation over repeated indices). This equation can be identified as a generalization of the Gibbs fundamental relation, e.g. see Equation (1). Thus, the mathematical structure of the Gibbs fundamental relation is not postulated in this paper. Instead it is derived from a mathematical property of the contact structure ![]() that defines the non-equilibrium thermodynamic state space. It is also not derived from the combination of both laws of thermodynamics, so it is a third essential component in the mathematical formulation of non-equili- brium thermodynamics. The canonical coordinate
that defines the non-equilibrium thermodynamic state space. It is also not derived from the combination of both laws of thermodynamics, so it is a third essential component in the mathematical formulation of non-equili- brium thermodynamics. The canonical coordinate ![]() will be called a thermodynamic potential, hence
will be called a thermodynamic potential, hence
Definition 2 [Thermodynamic potential]. The canonical coordinate![]() , whose change is directly proportional to the Gibbs contact 1-form
, whose change is directly proportional to the Gibbs contact 1-form![]() , is defined as the thermodynamic potential, viz.
, is defined as the thermodynamic potential, viz.![]() .
.
Symbols ![]() and
and ![]() in Equation (6) denote the conjugated coordinates, since they form
in Equation (6) denote the conjugated coordinates, since they form ![]() conjugated pairs of extensive and intensive quantities, or vice versa. The number of degrees of freedom in the Gibbs state space
conjugated pairs of extensive and intensive quantities, or vice versa. The number of degrees of freedom in the Gibbs state space ![]() is determined by the dimensions of the manifold
is determined by the dimensions of the manifold![]() , i.e.
, i.e.![]() . At this point it must be emphasized that
. At this point it must be emphasized that![]() ,
, ![]() and
and ![]() are coordinates in the Gibbs state space
are coordinates in the Gibbs state space ![]() that defines non-equilibrium thermodynamics. Equation (6) from Darboux’s theorem specifies only the functional relation between these non-equilibrium coordinates and captures the complete mathematical wealth of irreversible, non-equilibrium thermodynamics. One of the remaining issues will be to identify the physical meaning of the thermodynamic potential
that defines non-equilibrium thermodynamics. Equation (6) from Darboux’s theorem specifies only the functional relation between these non-equilibrium coordinates and captures the complete mathematical wealth of irreversible, non-equilibrium thermodynamics. One of the remaining issues will be to identify the physical meaning of the thermodynamic potential ![]() and the set of canonical coordinates
and the set of canonical coordinates ![]() and
and![]() . But before these coordinates can be identified, it is required to introduce the first and second law of thermodynamics.
. But before these coordinates can be identified, it is required to introduce the first and second law of thermodynamics.
3. Thermodynamic Laws
The distinction between exact and inexact 1-forms is an essential part of the mathematical formulation of the first and second laws of thermodynamics. The first law of thermodynamics states that for an arbitrary periodic process, the energy at the start and end of a complete period are identical. This statement complies with the definition of a non-equilibrium state function (e.g. see Definition 1). Both the amount of heat flow ![]() and work flow
and work flow ![]() are each path dependent quantities (viz. both are inexact 1-forms), so they are not conserved over a complete period in a periodic process. The first law of thermodynamics states that their sum is conserved.
are each path dependent quantities (viz. both are inexact 1-forms), so they are not conserved over a complete period in a periodic process. The first law of thermodynamics states that their sum is conserved.
Postulate 2 [First law of thermodynamics]. Summation of the inexact 1-forms for heat flow ![]() and work flow
and work flow ![]() results in an exact 1-form
results in an exact 1-form![]() , viz.
, viz.
![]() (7)
(7)
The crucial feature in the above postulate is, that the sum of two inexact 1-forms ![]() and
and ![]() results in an exact 1-form
results in an exact 1-form![]() . According to Definition 1 there exists then a non-equilibrium state function, which will be called internal energy
. According to Definition 1 there exists then a non-equilibrium state function, which will be called internal energy![]() , such that
, such that
![]() (8)
(8)
The internal energy ![]() is conserved over a complete period of an arbitrary periodic process due to the definition of the exterior derivative (viz.
is conserved over a complete period of an arbitrary periodic process due to the definition of the exterior derivative (viz.![]() , which is equivalent with the cycle integral).
, which is equivalent with the cycle integral).
In nature, it is observed that, for closed systems, processes are such that the system eventually approximates an equilibrium state. Once a system has obtained such an equilibrium state, interactions with the surroundings of the system are required to disturb this equilibrium. Hence, processes are directed towards a mathematical extremum, which corresponds with the equilibrium state, and this is irreversible when there is no interference from outside the system. Observations of these phenomena are for the first time published by Sadi Carnot (1796-1832, see [4] [21] ) and later mathematically formulated by Rudolf Clausius (see [22] [23] ). Clausius postulates, that a system in an equilibrium state has a macroscopic property, which he calls entropy ![]() and is mathematically defined by2
and is mathematically defined by2
![]() (9)
(9)
As is already stated before, the heat flow ![]() is a path dependent quantity and thus an inexact 1-form (viz.
is a path dependent quantity and thus an inexact 1-form (viz.![]() ). Frobenius integration theorem (see type 2) in Table 1 or [18] [24] [25] [26] ) is used in Clausius formulation to transform the inexact 1-form
). Frobenius integration theorem (see type 2) in Table 1 or [18] [24] [25] [26] ) is used in Clausius formulation to transform the inexact 1-form ![]() to the exact 1-form
to the exact 1-form![]() . From a mathematical perspective, the quantity
. From a mathematical perspective, the quantity ![]() is called an integrating factor, which is a different mathematical mechanism to obtain an exact 1-form compared to the one that is used
is called an integrating factor, which is a different mathematical mechanism to obtain an exact 1-form compared to the one that is used
![]()
Table 1. Overview of the Frobenius integrability condition (e.g. see [18] [24] [25] ).
in Postulate 2. In classical thermodynamics, the above definition is then often extended to non-equilibrium states by replacing the equal sign with an unequal sign or by adding some other term3. In such an approach, it is not clear that entropy ![]() is a non-equilibrium state function in thermodynamics, since it is not properly derived as an exact 1-form. This lack of mathematical accuracy might be one of the reasons why there are so many formulations of non-equilibrium thermodynamics.
is a non-equilibrium state function in thermodynamics, since it is not properly derived as an exact 1-form. This lack of mathematical accuracy might be one of the reasons why there are so many formulations of non-equilibrium thermodynamics.
![]() (10)
(10)
In these relations ![]() denotes the uncompensated heat in analogy to the “uncompensirten Verwandlung”
denotes the uncompensated heat in analogy to the “uncompensirten Verwandlung” ![]() in the work of Clausius [23] . The last relation with
in the work of Clausius [23] . The last relation with ![]() can only be found in his paper [28] , where his Equation (8) has the same structure as Equation (13) in this paper. Opposite to this paper,
can only be found in his paper [28] , where his Equation (8) has the same structure as Equation (13) in this paper. Opposite to this paper, ![]() is not identified as an integrating factor for the term
is not identified as an integrating factor for the term ![]() and the quantity
and the quantity ![]() itself is not specified in further detail.
itself is not specified in further detail.
One of the less famous pioneers in thermodynamics is the Greek mathematician Constantin Carathéodory (1800-1900). His work [30] [32] [33] on the use of Pfaffian equations for the mathematical formulation of thermodynamics has been crucified4, although it is one of the first attempts for a rigorous formalization of thermodynamics. In the second axiom in his 1909 paper [31] , he has an interesting formulation for the second law of thermodynamics that is based on geometrical considerations:
Axiom II: In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig approximiert werden können5.
Above axiom is in the literature also known as Carathéodory’s inaccessibility condition or as Carathéodory’s principle [30] . Notice that Carathéodory makes a statement about an arbitrary initial state, so in this axiom there is no explicit restriction to a thermodynamic equilibrium. But in his paper an adiabatic process is defined as a process where the systems remain in (phase) equilibrium when the deformable coordinates change6. So the heat transfer is not necessarily always equal to zero, which is in the textbook of Bamberg and Sternberg [13] [24] elegantly formulated by the mathematical concept of a null curve![]() , viz.
, viz.
![]() (11)
(11)
Based on the Frobenius integration theorem the second relation is derived from Axiom II and therefore also known as Carathéodory’s theorem [24] [35] [36] .
So modern interpretations of mathematical formulations for the definition of entropy in classical thermodynamics show, that the Frobenius integration theorem plays a crucial role. But opposite to the before mentioned formulations, in this paper Frobenius integration theorem is not applied to the inexact 1-form ![]() for heat flow. As is shown in both before mentioned cases, this would explicitly or implicitly require that there is an equilibrium state. Recall that the Gibbs contact 1-form
for heat flow. As is shown in both before mentioned cases, this would explicitly or implicitly require that there is an equilibrium state. Recall that the Gibbs contact 1-form ![]() is explicitly postulated to be non-degenerate, so it is not integrable by itself. Therefore, and this is a unique feature of the mathematical formulation in this paper, Frobenius integration theorem is applied to the difference between the heat flow and dissipation, viz.
is explicitly postulated to be non-degenerate, so it is not integrable by itself. Therefore, and this is a unique feature of the mathematical formulation in this paper, Frobenius integration theorem is applied to the difference between the heat flow and dissipation, viz.![]() .
.
Postulate 3 [Second law of thermodynamics]. The difference between the inexact 1-form ![]() for heat flow and the non-degenerating Gibbs contact 1-form
for heat flow and the non-degenerating Gibbs contact 1-form ![]() that represents the dissipation is completely integrable, viz.
that represents the dissipation is completely integrable, viz.
![]() (12)
(12)
Similar to the approach of Carathéodory, the concept of entropy is not defined in the above formulation for the second law of thermodynamics. Based on the integrability condition in Postulate 3 it can then be shown (see [18] [37] ), that there exists exactly one pair of conjugated coordinates. Here these coordinates are denoted by the absolute temperature ![]() and non-equilibrium entropy
and non-equilibrium entropy![]() , such that
, such that
![]() (13)
(13)
The exterior derivative of entropy ![]() is an exact 1-form due to the presence of the integrating factor
is an exact 1-form due to the presence of the integrating factor ![]() in the right-hand side of Equation (13). Hence, the existence of entropy
in the right-hand side of Equation (13). Hence, the existence of entropy ![]() as a non-equilibrium state function is based on a different mathematical mechanism compared to internal energy
as a non-equilibrium state function is based on a different mathematical mechanism compared to internal energy ![]() in the first law of thermodynamics. It is emphasized that both internal energy
in the first law of thermodynamics. It is emphasized that both internal energy ![]() and entropy
and entropy ![]() are introduced in this paper as non-equilibrium state functions. Finally, notice that both the absolute temperature
are introduced in this paper as non-equilibrium state functions. Finally, notice that both the absolute temperature ![]() and the Gibbs contact 1-form
and the Gibbs contact 1-form ![]() are nowhere equal to zero, so they are either everywhere positive or everywhere negative. Hence, in this paper the second law is not dominated by an inequality, but by the observation that certain physical quantities cannot be equal to zero.
are nowhere equal to zero, so they are either everywhere positive or everywhere negative. Hence, in this paper the second law is not dominated by an inequality, but by the observation that certain physical quantities cannot be equal to zero.
An integral part of the definition of a non-equilibrium state function is, that the initial value is identical to the final value at the end of a complete period in a periodic process. This means that the initial and final non-equilibrium state ![]() must be identical and consequently this has to hold for every macroscopic property
must be identical and consequently this has to hold for every macroscopic property![]() . As is already mentioned in Section 2, the likelihood that the statistically averaged value of every macroscopic property is recovered after a complete period in a real physical system is very small. But it is not equal to zero and thus it has to be considered as a limiting case in non-equilibrium thermodynamics. Consider Equation (13) for the case of a complete period, then
. As is already mentioned in Section 2, the likelihood that the statistically averaged value of every macroscopic property is recovered after a complete period in a real physical system is very small. But it is not equal to zero and thus it has to be considered as a limiting case in non-equilibrium thermodynamics. Consider Equation (13) for the case of a complete period, then
![]() (14)
(14)
Both the absolute temperature ![]() and the dissipation
and the dissipation ![]() are never equal to zero, hence their quotient is unequal to zero. This means that the right-hand side in the last relation is always either positive or negative. Consequently, the heat flow in a periodic process must have the same direction over every completed period and thus a heat flow is required to drive a periodic process. Or conversely, in non-equilibrium thermodynamics there does not exist a process that is both periodic and adiabatic at the same time. This is an intriguing observation, since Clausius’s formulation for entropy is based on periodic processes, while Carathéodory uses adiabatic processes to specify the second law of thermodynamics.
are never equal to zero, hence their quotient is unequal to zero. This means that the right-hand side in the last relation is always either positive or negative. Consequently, the heat flow in a periodic process must have the same direction over every completed period and thus a heat flow is required to drive a periodic process. Or conversely, in non-equilibrium thermodynamics there does not exist a process that is both periodic and adiabatic at the same time. This is an intriguing observation, since Clausius’s formulation for entropy is based on periodic processes, while Carathéodory uses adiabatic processes to specify the second law of thermodynamics.
4. Identification of Thermodynamic Coordinates
In this section the thermodynamic potential ![]() and the
and the ![]() pairs of conjugated coordinates
pairs of conjugated coordinates ![]() and
and ![]() in Equation (6) will be identified for the case of a single component, closed system (e.g. there is no mass transfer with the surrounding of the system). The basic elements for this identification are both laws of thermodynamics, but first the work flow
in Equation (6) will be identified for the case of a single component, closed system (e.g. there is no mass transfer with the surrounding of the system). The basic elements for this identification are both laws of thermodynamics, but first the work flow ![]() has to be specified in more detail. In general, every 1-form can be written as a linear combination of the corresponding coordinates. The coordinates for work are force
has to be specified in more detail. In general, every 1-form can be written as a linear combination of the corresponding coordinates. The coordinates for work are force ![]() and displacement
and displacement![]() , thus the inexact 1-form
, thus the inexact 1-form ![]() for the work flow can be written as
for the work flow can be written as
![]() (15)
(15)
This equation does not add new information to the presented mathematical framework of non-equilibrium thermodynamics. It only specifies the set of coordinates that determines the work flow![]() . Symbols
. Symbols ![]() and
and ![]() (with
(with![]() ) denote respectively generalized thermodynamic forces and displacements7, where blackboard fonts are used to denote extensive quantities. The indices are
) denote respectively generalized thermodynamic forces and displacements7, where blackboard fonts are used to denote extensive quantities. The indices are ![]() and
and ![]() for the general case, but for a single component, closed system it will be shown that
for the general case, but for a single component, closed system it will be shown that![]() . Combine above equation with Equations (8) and (13), then the following equation can be obtained
. Combine above equation with Equations (8) and (13), then the following equation can be obtained
![]() (16)
(16)
By comparing this equation with Equation (6), one could argue that the thermodynamic potential and the set of conjugated coordinates are identified. But this identification would not be a sound mathematical proof due to the presence of the contact 1-form![]() . Furthermore, this reasoning obscures another important thermodynamic quantity, which is already hidden in the three proposed postulates.
. Furthermore, this reasoning obscures another important thermodynamic quantity, which is already hidden in the three proposed postulates.
Opposite to most textbooks on thermodynamics, in this paper the definition of the Gibbs free energy ![]() is not one of the building blocks for the mathematical formulation of thermodynamics. Instead the Gibbs free energy
is not one of the building blocks for the mathematical formulation of thermodynamics. Instead the Gibbs free energy ![]() is derived from the combination of the three proposed postulates in non-equilibrium thermodynamics and the above general specification for the work flow
is derived from the combination of the three proposed postulates in non-equilibrium thermodynamics and the above general specification for the work flow![]() .
.
Theorem 1 [Gibbs free energy]. For a single component, closed system the thermodynamic potential ![]() in the generalized fundamental relation (e.g. Equation (6)) is the so-called Gibbs free energy
in the generalized fundamental relation (e.g. Equation (6)) is the so-called Gibbs free energy![]() , viz.
, viz.
![]() (17)
(17)
The corresponding pairs of conjugated coordinates ![]() and
and ![]() are:
are:
![]() (18)
(18)
Proof. The proof starts with the combination of the generalized Gibbs fundamental relation and the second law of thermodynamics by substituting Equation (13) into Equation (6). Then replace the 1-form ![]() for heat flow using the first law of thermodynamics. Finally, use the above specification of the work flow
for heat flow using the first law of thermodynamics. Finally, use the above specification of the work flow ![]() to obtain
to obtain
![]() (19)
(19)
Notice that due to these steps the Gibbs contact 1-form ![]() is removed from the above equation, so the Gibbs fundamental relation is reduced to a Pfaffian equation where
is removed from the above equation, so the Gibbs fundamental relation is reduced to a Pfaffian equation where![]() . This is the essential step that provides crucial features for the following derivation.
. This is the essential step that provides crucial features for the following derivation.
The next step in this proof is based on a unique property of thermodynamic properties: thermodynamic properties are either extensive or intensive quantities. Extensive quantities are proportional to the size (or extend) of the thermodynamic system and therefore scalable, while intensive quantities are independent of the size of the system. The total volume ![]() of the system is used here to scale every extensive quantity in Equation (19), hence
of the system is used here to scale every extensive quantity in Equation (19), hence
![]() (20)
(20)
Consider the case that all conjugate coordinates denoted by ![]() are extensive quantities (viz. then
are extensive quantities (viz. then![]() ) and all conjugated coordinates denoted by
) and all conjugated coordinates denoted by ![]() are intensive quantities8. Substitute every relation in Equation (20) to the corresponding terms in Equation (19) and apply the product rule of differentiation. Rearrange the resulting equation by collecting all terms with either
are intensive quantities8. Substitute every relation in Equation (20) to the corresponding terms in Equation (19) and apply the product rule of differentiation. Rearrange the resulting equation by collecting all terms with either ![]() or
or ![]() to obtain
to obtain
![]() (21)
(21)
The total volume ![]() of a thermodynamic system is larger than zero, while the change of volume
of a thermodynamic system is larger than zero, while the change of volume ![]() can be positive, negative or equal to zero. So, for an arbitrary system, above equation can only hold when both terms between the brackets are equal to zero. Hence, the following two relations have been derived
can be positive, negative or equal to zero. So, for an arbitrary system, above equation can only hold when both terms between the brackets are equal to zero. Hence, the following two relations have been derived
![]() (22)
(22)
and
![]() (23)
(23)
Equation (23)2 is obtained by multiplying Equation (23)1 with the total volume![]() . The thermodynamic potential
. The thermodynamic potential![]() , as it is specified in Equation (23), is called the Gibbs free energy and is therefore denoted by symbol
, as it is specified in Equation (23), is called the Gibbs free energy and is therefore denoted by symbol![]() .
.
The final step in this proof is to identify the set of conjugated coordinates ![]() and
and![]() . Apply therefore the exterior derivative to Equation (23)2 with
. Apply therefore the exterior derivative to Equation (23)2 with ![]() and use again the product rule of differentiation, then
and use again the product rule of differentiation, then
![]() (24)
(24)
This is again a Pfaffian equation for a thermodynamic state function, either for the Gibbs energy ![]() or the internal energy
or the internal energy![]() . Subtract then Equation (19) from the above Pfaffian equation, which results in the following relation
. Subtract then Equation (19) from the above Pfaffian equation, which results in the following relation
![]() (25)
(25)
There are ![]() conjugated pairs of intensive and extensive quantities in the above equation, of which the
conjugated pairs of intensive and extensive quantities in the above equation, of which the ![]() intensive quantities
intensive quantities ![]() must be identified. Thermodynamic state variables can change independently and in the Gibbs state space
must be identified. Thermodynamic state variables can change independently and in the Gibbs state space ![]() there are exactly
there are exactly ![]() conjugate pairs of intensive and extensive quantities (see Darboux’s theorem on page 5). Hence, the set of specified intensive quantities
conjugate pairs of intensive and extensive quantities (see Darboux’s theorem on page 5). Hence, the set of specified intensive quantities ![]() must be identical to the set
must be identical to the set ![]() that must be identified in this proof. Apply this insight to above equation and rearrange to get
that must be identified in this proof. Apply this insight to above equation and rearrange to get
![]() (26)
(26)
Again, for an arbitrary thermodynamic process the above equation can only hold when all terms between brackets are equal to zero. The set of extensive conjugated coordinates ![]() is therefore also determined.
is therefore also determined. ![]()
Equation (17), which is in this paper derived in the above proof, is in the literature also known as Euler’s relation (e.g. see [38] [39] [40] ). Substitute Equation (17) and the pairs of conjugated coordinates in Theorem 1 into Equation (6) to obtain the following generalized formulation for the Gibbs fundamental relation
![]() (27)
(27)
Equation (16) can be derived by subtracting the above equation from Equation (27), where![]() . The equation can also be derived by repeating the proof of Theorem 1 for the reversed case, where every
. The equation can also be derived by repeating the proof of Theorem 1 for the reversed case, where every ![]() is an intensive quantity and every
is an intensive quantity and every ![]() is an extensive quantity (viz. then
is an extensive quantity (viz. then![]() ). This case shows that the thermodynamic potential is specified by the following Euler equation
). This case shows that the thermodynamic potential is specified by the following Euler equation
![]() (28)
(28)
Both Equations (16) and (27) are implementations of Equation (6) for single component, closed systems, which is therefore a generic formulation of the third key element of thermodynamics (besides both laws of thermodynamics). Both equations confirm that Gibbs free energy ![]() and internal energy
and internal energy ![]() are thermodynamic potentials according to Definition 2. Finally, notice that both equations contain identical 1-forms, viz.
are thermodynamic potentials according to Definition 2. Finally, notice that both equations contain identical 1-forms, viz. ![]() and the Gibbs contact 1-form
and the Gibbs contact 1-form![]() .
.
5. Equilibrium Constraint
So far, this paper has been focused on the general case of non-equilibrium states and arbitrary irreversible processes. For an isolated system (then there are no interactions with the surroundings), it is in nature observed, that the macro- scopic state of the system does not change any more if one waits sufficiently long. The corresponding thermodynamic state is called the equilibrium state of the system for which the change of a state function ![]() is equal to zero, hence
is equal to zero, hence
![]() (29)
(29)
Molecules do not stop moving in such an equilibrium state; there are many fluctuations of the microstates, which are not visible on the macroscopic level. On a macroscopic level, any perturbation away of an equilibrium state requires some kind of exchange with the surrounding of the system. The above equation implements a mathematical extremum, which is not present in the proposed mathematical framework for non-equilibrium thermodynamics due to the mathematical properties of the Gibbs contact 1-form![]() . To further clarify this point, consider Equation (13) for the case of a closed system without any heat flow, then
. To further clarify this point, consider Equation (13) for the case of a closed system without any heat flow, then
![]() (30)
(30)
The absolute temperature ![]() and the Gibbs contact 1-form
and the Gibbs contact 1-form ![]() are defined to be everywhere unequal to zero. So, in the case of non-equilibrium thermodynamics, the change of entropy
are defined to be everywhere unequal to zero. So, in the case of non-equilibrium thermodynamics, the change of entropy ![]() cannot be equal to zero, as is required for an equilibrium state.
cannot be equal to zero, as is required for an equilibrium state.
Based on the above considerations it becomes clear, that an additional mathematical construct is required to embed equilibrium thermodynamics within the proposed mathematical framework. Consider therefore an arbitrary irreversible process ![]() and some other kind of process
and some other kind of process![]() . Equilibrium thermodynamics is then formulated by the Legendre submanifold
. Equilibrium thermodynamics is then formulated by the Legendre submanifold![]() , which is induced by the pull-back of a map
, which is induced by the pull-back of a map ![]() applied to the Gibbs contact 1-form
applied to the Gibbs contact 1-form ![]() [16] [41] [42] [43] .
[16] [41] [42] [43] .
Postulate 4 [Equilibrium constraint]. There exists an equilibrium map
![]() , who’s pull-back is governed by the equilibrium constraint
, who’s pull-back is governed by the equilibrium constraint
![]() (31)
(31)
This postulate can also be found in the original work of Hermann [15] and Mrugała [44] on thermodynamics in a geometric framework. The modern literature (e.g. see [15] [16] [43] [44] [45] [46] ) uses the Legendre manifold ![]() to derive classical relations in equilibrium thermodynamics. For instance, Mrugała writes9: A Legendre manifold
to derive classical relations in equilibrium thermodynamics. For instance, Mrugała writes9: A Legendre manifold ![]() of
of ![]() is a maximum dimensional integral manifold of the Pfaffian equation
is a maximum dimensional integral manifold of the Pfaffian equation![]() . Classical formulations follow the approach of Carathéodory, which is based on Pfaffian equations and exact 1-forms (e.g. see [18] [30] [31] [33] ).
. Classical formulations follow the approach of Carathéodory, which is based on Pfaffian equations and exact 1-forms (e.g. see [18] [30] [31] [33] ).
The distinction between the equilibrium Legendre state space ![]() and the non-equilibrium Gibbs state space
and the non-equilibrium Gibbs state space ![]() can be clarified based on the visualization in Figure 1. The figure shows two equilibrium hypersurfaces denoted by
can be clarified based on the visualization in Figure 1. The figure shows two equilibrium hypersurfaces denoted by ![]() and
and![]() , which are both a function of the coordinates
, which are both a function of the coordinates ![]() and
and![]() . There are indefinitely many equilibrium hypersurfaces, but some of them have at one equilibrium state identical partial derivatives (e.g. see point
. There are indefinitely many equilibrium hypersurfaces, but some of them have at one equilibrium state identical partial derivatives (e.g. see point ![]() in the figure). A thermodynamic process is reversible if it connects only equilibrium states that are on the same equilibrium hypersurface (viz. the solid lines denoted by
in the figure). A thermodynamic process is reversible if it connects only equilibrium states that are on the same equilibrium hypersurface (viz. the solid lines denoted by ![]() and
and![]() ). A process becomes irreversible when two neighboring equilibrium states do not belong to the same equilibrium hypersurface. The transition between two equilibrium hypersurfaces requires that the thermodynamic system has been in a non-equilibrium state. For instance, the non-equilibrium states which connect the equilibrium states
). A process becomes irreversible when two neighboring equilibrium states do not belong to the same equilibrium hypersurface. The transition between two equilibrium hypersurfaces requires that the thermodynamic system has been in a non-equilibrium state. For instance, the non-equilibrium states which connect the equilibrium states ![]() and
and ![]() (here shown as a jump by the dotted line). Notice that these non-equilibrium states depend, besides
(here shown as a jump by the dotted line). Notice that these non-equilibrium states depend, besides ![]() and
and![]() , also on the corresponding conjugated coordinates
, also on the corresponding conjugated coordinates ![]() and
and![]() .
.
Next some results will be obtained for the case of equilibrium thermodynamics. An underline will be used in this paper to denote symbols that refer to an
equilibrium state on the Legendre submanifold![]() . Apply first the pull-back of the equilibrium map
. Apply first the pull-back of the equilibrium map ![]() to the change of the thermodynamic potential
to the change of the thermodynamic potential ![]() in Equation (6), then
in Equation (6), then
![]() (32)
(32)
Then a similar procedure can be applied to pairs of conjugated coordinates in Equation (6), where the 1-form ![]() becomes equal to
becomes equal to
![]() (33)
(33)
Thus, application of the equilibrium map in Postulate 4 to the generalized Gibbs fundamental relation in Equation (6) results in
![]() (34)
(34)
The last relation is called a Pfaffian equation, where the 1-form ![]() is an exact 1-form (see also Definition 1). A state function
is an exact 1-form (see also Definition 1). A state function ![]() is in general a 0-form, where the evaluation of the exterior derivative is straightforward (e.g. see [17] [25] [47] ). Select the set
is in general a 0-form, where the evaluation of the exterior derivative is straightforward (e.g. see [17] [25] [47] ). Select the set ![]() with
with ![]() as coordinates, then
as coordinates, then
![]() (35)
(35)
The relations in Equation (35)3 follow from the combination of Equations (34)2 and (35)2, so these relations are only valid for equilibrium thermodynamics. To further clarify this point, consider internal energy ![]() as it is defined in Postulate 2 by the exact 1-form
as it is defined in Postulate 2 by the exact 1-form![]() . Evaluate Equation (35)2 for the non-equili- brium case10 and combine the result with Equation (16) to obtain
. Evaluate Equation (35)2 for the non-equili- brium case10 and combine the result with Equation (16) to obtain
![]() (36)
(36)
Since the Gibbs contact 1-form ![]() is everywhere unequal to zero, it is not possible to derive relations from the terms between brackets. This observation confirms that the relations in Equation (35)3 do not hold for non-equilibrium thermodynamics.
is everywhere unequal to zero, it is not possible to derive relations from the terms between brackets. This observation confirms that the relations in Equation (35)3 do not hold for non-equilibrium thermodynamics.
Another example of interesting formulations in equilibrium thermodynamics are the so-called Maxwell relations (e.g. see [3] [7] [48] ). Apply the equilibrium constraint in Postulate 4 to Equation (16), which reduces to the following Pfaffian equation on the Legendre submanifold ![]()
![]() (37)
(37)
The second relation shows the correct set of canonical coordinates to completely specify internal energy ![]() in the case of equilibrium thermodynamics. Apply this knowledge to Equation (35)2 and substitute the result in the above Pfaffian equation to obtain
in the case of equilibrium thermodynamics. Apply this knowledge to Equation (35)2 and substitute the result in the above Pfaffian equation to obtain
![]() (38)
(38)
Mixed derivatives that originate from a closed 1-form are symmetric11. So, differentiate the first relation with respect to volume ![]() and the second relation with respect to entropy
and the second relation with respect to entropy![]() , which results in
, which results in
![]() (41)
(41)
![]() (39)
(39)
Based on the Poincaré lemma, it can be proven that every exact 1-form is also a closed 1-form (see [17] [25] ). Hence ![]() is a closed 1-form, which means that its exterior derivative is equal to zero. Apply the exterior derivative to the case of the above example, which results in
is a closed 1-form, which means that its exterior derivative is equal to zero. Apply the exterior derivative to the case of the above example, which results in
![]() (40)
(40)
The term between parentheses has to vanish since![]() . Equation (35)2 shows that the coefficients
. Equation (35)2 shows that the coefficients ![]() and
and ![]() are equal to the partial derivatives of the generating function
are equal to the partial derivatives of the generating function![]() , which results in the mixed partial derivatives (See also [16] ).
, which results in the mixed partial derivatives (See also [16] ).
This is one of the familiar four Maxwell relations [3] [5] [6] [7] [48] , where it is shown in this paper that they can be derived only for the case of equilibrium thermodynamics. Finally, apply the pull-back of map ![]() to Equation (27) to obtain the following Gibbs fundamental relation on the Legendre submanifold
to Equation (27) to obtain the following Gibbs fundamental relation on the Legendre submanifold ![]()
![]() (42)
(42)
So, the thermodynamic potential (viz. here![]() ) is a state function according to Definition 1 in the case of equilibrium thermodynamics. Notice that Equation (6) is not a Pfaffian equation due to the presence of the Gibbs contact 1-form
) is a state function according to Definition 1 in the case of equilibrium thermodynamics. Notice that Equation (6) is not a Pfaffian equation due to the presence of the Gibbs contact 1-form![]() , which is everywhere unequal to zero. Consequently the 1-form
, which is everywhere unequal to zero. Consequently the 1-form ![]() in Equation (6) is neither an exact nor a closed 1-form. The thermodynamic potential
in Equation (6) is neither an exact nor a closed 1-form. The thermodynamic potential ![]() is in the presented mathematical framework for non-equilibrium thermodynamics not explicitly postulated as a state function that complies with Definition 1.
is in the presented mathematical framework for non-equilibrium thermodynamics not explicitly postulated as a state function that complies with Definition 1.
6. Conclusions
Classical Non-Equilibrium Thermodynamics (CNET) is the science of phenomenological changes in the state of systems. Especially these changes make the tools of differential geometry extremely suited for a rigorous mathematical formulation. The presented formulation for non-equilibrium thermodynamics consists of the following three base postulates:
・ there exists a non-equilibrium thermodynamic phase space (Gibbs state space),
・ energy is conserved (first law of thermodynamics),
・ the difference between heat flow and dissipation is completely integrable (second law of thermodynamics).
The thermodynamic phase space is built upon macroscopic properties of a system. Neither temporal nor spatial coordinates are considered in the presented mathematical formulation of non-equilibrium thermodynamics. The direction of processes is not implemented by an explicit inequality in the second law of thermodynamics. Instead an implicit reverse is applied: there is a physical quantity that is nowhere equal to zero, viz. the dissipation of energy. Furthermore, no explicit signs are assigned to nowhere vanishing physical quantities. Still this formulation shows clearly that there can only be a periodic process if and only if it is driven by the appropriate heat flow.
Together with the definition of a state function, other relations are derived based on the mathematical properties of this formulation. The mathematical structure for the Gibbs fundamental relation follows from the Gibbs state space. Through a clever combination with both laws of thermodynamics it can be proven that the thermodynamic potential is specified by the Gibbs free energy. Other coordinates in the formulation of the Gibbs fundamental relation are identified for a single component, closed system. Notice that there is neither in the postulates, nor in the derivation of the mathematical framework for non- equilibrium thermodynamics any assumption that restricts the arbitrary processes to certain classes (e.g. periodic, adiabatic, sufficiently slow, etc.).
The introduction of an equilibrium state is postponed until the final section, where it is introduced as an extremum (viz. no change of a state function). This is mathematically implemented by the pull-back of an equilibrium map with the condition that there is no dissipation of energy. Such an elaborate construction is required, because the dissipation of energy is in the general case of non- equilibrium thermodynamics by definition unequal to zero. For the case of an equilibrium state, the Gibbs fundamental relation reduces to a Pfaffian equation. It is shown that the Maxwell relations in thermodynamics can be derived only for the case of an equilibrium state.
NOTES
![]()
1The macroscopic property has obtained an identical statistically averaged value compared to its initial value, but this does not mean that the probability distribution is identical to its original distribution (nor that the microstates are identical). This observation is a severe release of constraints compared to traditional equilibrium based approaches.
![]()
2Here the concepts and notation of this paper are used, where an equilibrium state is denoted by underlined symbols (see also Section 5).
3In this context is the work of Eu [27] [28] [29] very interesting. He is aware that the Clausius definition for entropy holds only for reversible processes (e.g. equilibrium state). Eu introduces therefore a new thermodynamic quantity Calortropy![]() , which is specified by
, which is specified by
4See the Appendix to the Historical Indroit: Failure of Carathéodory’s attempt to set the house in order’ in the textbook on Rational thermodynamics by Truesdell (pp. 49-57 in [34] ).
5In every neighborhood of an arbitrary thermodynamic state there exist states that cannot be approached by an adiabatic process.
6Based on three assumption he introduces a simple system together with a quasi-static change of state, which is in his formulation another reference to an equilibrium state.
7Examples are: elastic deformation ![]() (with mechanical stress
(with mechanical stress ![]() and strain
and strain![]() ), surface change
), surface change ![]() (with surface tension
(with surface tension ![]() and surface area
and surface area![]() ), electrical polarization
), electrical polarization ![]() (with electric field
(with electric field ![]() and electric dipole moment
and electric dipole moment![]() ), magnetic work
), magnetic work ![]() (with magnetic field
(with magnetic field ![]() and magnetic dipole moment
and magnetic dipole moment![]() ) and galvanic element
) and galvanic element ![]() (with electrical potential
(with electrical potential ![]() and electrical charge
and electrical charge![]() ).
).
8In principle the following derivation is independent of which of the conjugated coordinates is extensive or intensive, as long as every pair contains of an extensive and an intensive quantity. But it is exactly this particular case, which will reveal that the thermodynamic potential ![]() is equal to the familiar Gibbs free energy
is equal to the familiar Gibbs free energy![]() . The result of the reverse selection of intensive and extensive quantities is shown at the end of this section.
. The result of the reverse selection of intensive and extensive quantities is shown at the end of this section.
9Quote from [44] , but modified with the conventions of this paper.
10It is here tacitly assumed that![]() , which has to be proven for the non-equilib- rium case.
, which has to be proven for the non-equilib- rium case.
11Definition 1 introduced the non-equilibrium state function as an exact 1-form and Equation (34)1 shows that the 1-form ![]() in a Pfaffian equation is also exact. The mathematical concept of an exact 1-form originates from the area of differential manifolds (e.g. see [20] [47] [49] [50] [51] ). An arbitrary exact 1-form
in a Pfaffian equation is also exact. The mathematical concept of an exact 1-form originates from the area of differential manifolds (e.g. see [20] [47] [49] [50] [51] ). An arbitrary exact 1-form ![]() can be constructed as a linear combination of the differentials of the coordinates
can be constructed as a linear combination of the differentials of the coordinates![]() , i.e. for
, i.e. for ![]() the 1-form
the 1-form ![]() can be written as
can be written as