1. Introduction
The Weibull distribution (WD) submitted by Weibull [1] , is an important and popular distribution for modeling lifetime data where the hazard rate function is monotone. Recently, new classes of distributions were based on modifications of the Weibull distribution (WD) to provide a good fit to data set with bathtub hazard failure rate Xie and Lai [2] . The Modified Weibull (MW) distribution has been derived by Lai et al. [3] and Sarhan and Zaindin [4] . Moreover the Beta-Weibull (BW) distribution has been studied by Famoye et al. [5] , Beta modified Weibull (BMW) distribution, see Silva et al. [6] and Nadarajah et al. [7] and Kumaraswamy Weibull (KW) distribution, see Cordeiro et al. [8] . Furthermore, many generalizations of the Weibull distribution are investigated like a Generalized modified Weibull (GMW) distribution, Carrasco et al. [9] and Exponentiated modified Weibull extension (EMWE) distribution, Sarhan and Apaloo [10] . Also we can find good review of these models in Pham and Lai [11] and Murthy et al. [12] .
The Flexible Weibull (FWE) distribution (Bebbington et al. [13] ) has many applications in life testing experiments, applied statistics, reliability analysis and clinical studies. For more details on this distribution, see [13] . If 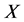 is a random variable and it has the Flexible Weibull Extension (FWE) distribution with parameters
is a random variable and it has the Flexible Weibull Extension (FWE) distribution with parameters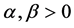 , then it’s probability density function (pdf) is given by
, then it’s probability density function (pdf) is given by
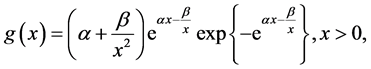 (1)
(1)
while the cumulative distribution function (cdf) is given by
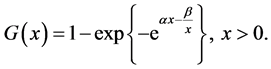 (2)
(2)
The survival function is given by the equation
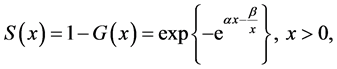 (3)
(3)
and the hazard rate function is
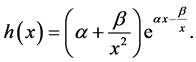 (4)
(4)
In this article, a new generalization of the Flexible Weibull Extension (FWE) distribution called exponential flexible Weibull extension (EFWE) distribution is derived. Using the exponential generator applied to the odds ratio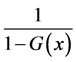 , such as the expo-
, such as the expo-
nential Pareto distribution by AL-Kadim and Boshi [14] , exponential lomax distribution by El-Bassiouny et al. [15] . If 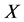 is a random variable and
is a random variable and 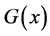 is the baseline cumulative distribution function with probability density function
is the baseline cumulative distribution function with probability density function 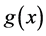 and the exponential cumulative distribution function is
and the exponential cumulative distribution function is
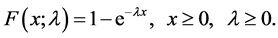 (5)
(5)
By using Equation (5) and replacing the random variable  with ratio
with ratio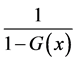 .
.
The cdf of exponential generalized distribution is defined by AL-Kadim and Boshi [14] and El-Bassiouny et al. [15]
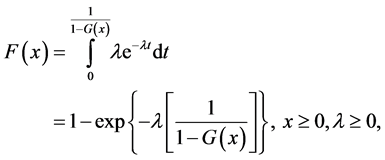 (6)
(6)
where 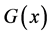 is a baseline cdf. Hence the pdf corresponding to Equation (6) is given as
is a baseline cdf. Hence the pdf corresponding to Equation (6) is given as
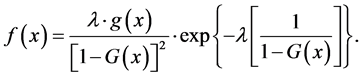 (7)
(7)
This article is organized as follows. The cumulative function, density function and hazard function of the exponential flexible Weibull extension (EFWE) distribution are defined in Section 2. Some of statistical properties including, quantile function and simulation, the mode, median, the skewness and kurtosis and 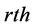 moments are presented in Sections 3. The moment generating function (mgf) is derived in Sections 4. The order statistics is determined in Section 5. The maximum likelihood estimation of the parameters is obtained in Section 6. Real data sets are analyzed in Section 7. Moreover, we discuss the results and compare it with existing distributions. Finally, we introduce the conclusion of our results.
moments are presented in Sections 3. The moment generating function (mgf) is derived in Sections 4. The order statistics is determined in Section 5. The maximum likelihood estimation of the parameters is obtained in Section 6. Real data sets are analyzed in Section 7. Moreover, we discuss the results and compare it with existing distributions. Finally, we introduce the conclusion of our results.
2. Definition of the EFWE Distribution
We define in this section three parameters of the Exponential Flexible Weibull Extension EFWE ![]() distribution. Using
distribution. Using ![]() Equation (2) and
Equation (2) and ![]() Equation (1) in Equation (6) and Equation (7) to obtain the cdf and pdf of EFWE distribution. The cumulative distribution function cdf of the Exponential Flexible Weibull Extension distribution (EFWE) is given by
Equation (1) in Equation (6) and Equation (7) to obtain the cdf and pdf of EFWE distribution. The cumulative distribution function cdf of the Exponential Flexible Weibull Extension distribution (EFWE) is given by
![]() (8)
(8)
The pdf corresponding to Equation (8) is given by
![]() (9)
(9)
where ![]() and
and ![]() are two additional shape parameters.
are two additional shape parameters.
The survival function![]() , hazard rate function
, hazard rate function![]() , reversed hazard rate function
, reversed hazard rate function ![]() and cumulative hazard rate function
and cumulative hazard rate function ![]() of
of ![]() are given by
are given by
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
respectively, ![]() and
and![]() .
.
Figures 1-6 display the cdf, pdf, survival function, hazard rate function, reversed hazard rate function and cumulative hazard rate function of the EFWE ![]() distribution for some parameter values.
distribution for some parameter values.
3. Some Statistical Properties
Some statistical properties for the EFWE distribution, such as quantile and simulation
![]()
Figure 1. The cdf of the EFWE for different values of parameters.
![]()
Figure 2. The pdf of the EFWE for different values of parameters.
![]()
Figure 3. The ![]() of the EFWE for different values of parameters.
of the EFWE for different values of parameters.
![]()
Figure 4. The ![]() of the EFWE for different values of parameters.
of the EFWE for different values of parameters.
![]()
Figure 5. The ![]() of the EFWE for different values of parameters.
of the EFWE for different values of parameters.
![]()
Figure 6. The ![]() of the EFWE for different values of parameters.
of the EFWE for different values of parameters.
median, the mode, moments, the skewness and kurtosis are given as follows.
3.1. The Quantile and Simulation
Suppose the random variable ![]() is the quantile of the EFWE distribution given by
is the quantile of the EFWE distribution given by
![]() (14)
(14)
Using the distribution function of EFWE distribution, from (8), we have
![]() (15)
(15)
where
![]() (16)
(16)
So, the simulation of the EFWE distribution random variable is straightforward. We obtain the random variable ![]() by solve the Equation (15) as follows form
by solve the Equation (15) as follows form
![]() (17)
(17)
Since the median is ![]() quantile then by setting
quantile then by setting ![]() in Equation (15), we can obtain the median
in Equation (15), we can obtain the median ![]() of EFWE distribution.
of EFWE distribution.
3.2. The Mode of EFWE
The mode of the EFWE distribution can be obtained by differentiating its probability density function in Equation (9) with respect to ![]() and equaling it to zero. So the mode of the EFWE is the solution of the following equation
and equaling it to zero. So the mode of the EFWE is the solution of the following equation
![]() (18)
(18)
The EFWE distribution has only one peak, then this distribution is a unimodal distribution. Figure 2 shows that Equation (18) has only one solution. It is difficult to get an explicit solution of Equation (18). Therefore, it can be solved numerically. Some values of median and mode for various values of the parameters ![]() and
and ![]() are calculated in Table 1.
are calculated in Table 1.
3.3. The Skewness and Kurtosis
In this subsection, we can obtain the skewness and kurtosis based on the quantile
![]()
Table 1. The median and mode for EFWE![]() .
.
measures. The Bowely’s skewness (Kenney and Keeping [16] ) is given by
![]() (19)
(19)
and the Moors Kurtosis (Moors [17] ) can be obtained, based on octiles, as follows
![]() (20)
(20)
where the ![]() is quantile function.
is quantile function.
3.4. The Moments
Here, we derive the ![]() moment for EFWE distribution in the next theorem
moment for EFWE distribution in the next theorem
Theorem 1. If ![]() has EFWE
has EFWE ![]() distribution, then the
distribution, then the ![]() moments of random variable
moments of random variable![]() , is given by
, is given by
![]() (21)
(21)
Proof. From the definition of the moments, we know that the ![]() moment of the random variable
moment of the random variable ![]() with the pdf
with the pdf ![]() is given by
is given by
![]() (22)
(22)
Substituting from Equation (9) into Equation (22) we get
![]()
the expansion of ![]() is
is
![]()
then we have
![]()
using series expansion of![]() ,
,
![]()
hence, we obtain
![]()
using series expansion of![]() ,
,
![]()
we have
![]()
using the definition of the gamma function (Zwillinger [18] ), in the follows form,
![]()
Finally, the ![]() moment of EFWE distribution is obtained in the form
moment of EFWE distribution is obtained in the form
![]()
This completes the proof. W
4. The Moment Generating Function
The moment generating function (mgf) of the EFWE distribution is given by theorem 2.
Theorem 2. If ![]() is a random variable from EFWE
is a random variable from EFWE ![]() distribution, then its moment generating function is
distribution, then its moment generating function is
![]() (23)
(23)
Proof. The moment generating function (mgf) of the random variable ![]() with the pdf
with the pdf ![]() is
is
![]() (24)
(24)
using series expansion of![]() , we obtain
, we obtain
![]() (25)
(25)
Substituting from Equation (21) into Equation (25) we obtain the moment generating function (mgf) of EFWE distribution in the form
![]()
This completes the proof. W
5. The Order Statistics
In this section, we derive closed form expressions for the probability density function pdf of the ![]() order statistic of the EFWE distribution. Suppose
order statistic of the EFWE distribution. Suppose ![]() denote the order statistics obtained from a random sample
denote the order statistics obtained from a random sample ![]() which taken from a continuous population with cumulative distribution function
which taken from a continuous population with cumulative distribution function ![]() and probability density function
and probability density function![]() , then the pdf of
, then the pdf of ![]() is as follows
is as follows
![]() (26)
(26)
where ![]() and
and ![]() are the probability density function and cumulative distribution function of EFWE
are the probability density function and cumulative distribution function of EFWE ![]() distribution given by Equation (9) and Equation (8) respectively,
distribution given by Equation (9) and Equation (8) respectively, ![]() is the Beta function and
is the Beta function and![]() , also we define first order statistics
, also we define first order statistics![]() , and the last order statistics as
, and the last order statistics as![]() , where
, where ![]() for all
for all![]() . Using the binomial expansion of
. Using the binomial expansion of ![]()
![]() (27)
(27)
Substituting from Equation (27) into Equation (26), we have
![]() (28)
(28)
Substituting from Equation (8) and Equation (9) into Equation (28), we obtain
![]() (29)
(29)
Relation (29) shows that ![]() is the weighted average of the Exponential Flexible Weibull Extension distribution with different shape parameters.
is the weighted average of the Exponential Flexible Weibull Extension distribution with different shape parameters.
6. Parameters Estimation
In this section, point and interval estimation of the unknown parameters of the EFWE distribution are derived by using the method of maximum likelihood based on a complete sample.
6.1. Maximum Likelihood Estimation
Let ![]() denote a random sample of complete data from the EFWE distribution. The Likelihood function is given as
denote a random sample of complete data from the EFWE distribution. The Likelihood function is given as
![]() (30)
(30)
substituting from (9) into (30), we have
![]()
The log-likelihood function is
![]() (31)
(31)
The maximum likelihood estimation of the parameters are obtained by differentiating the log-likelihood function ![]() with respect to the parameters
with respect to the parameters ![]() and
and ![]() and setting the result to zero, as follows
and setting the result to zero, as follows
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
The MLEs can be obtained by solving the nonlinear Equations (32)-(34), numerically for ![]() and
and ![]() by using Mathcad program.
by using Mathcad program.
6.2. Asymptotic Confidence Bounds
The asymptotic confidence intervals can be obtained when the parameters ![]() and
and ![]() are positive as the maximum likelihood estimations of the unknown parameters
are positive as the maximum likelihood estimations of the unknown parameters ![]() but can’t be obtained in closed forms. So, by using variance covariance matrix
but can’t be obtained in closed forms. So, by using variance covariance matrix ![]() see (Lawless [19] ), where the
see (Lawless [19] ), where the ![]() is inverse of the observed information matrix which defined as follows
is inverse of the observed information matrix which defined as follows
![]() (35)
(35)
where
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
Furthermore, the ![]() confidence intervals of the parameters
confidence intervals of the parameters ![]() can be obtained by using variance matrix as the following forms
can be obtained by using variance matrix as the following forms
![]()
where![]() , and
, and ![]() denote the upper
denote the upper ![]() -th percent of the standard normal distribution.
-th percent of the standard normal distribution.
7. Application
In this application, we will analysis a real data set given by Aarset [22] , see Table 2, using the EFWE ![]() distribution and compare it with the other fitted distributions like a flexible Weibull extension (FWE) distribution, Weibull (W) distribution, linear failure rate (LFR) distribution, Exponentiated Weibull (EW) distribution, generalized linear failure rate (GLFR) distribution and Exponentiated Flexible Weibull (EFW) distribution by using Kolmogorov Smirnov (K-S) statistic, P-value, Akaike information criterion (AIC), as well as Akaike Information Criterion with correction (AICC), see [20] and also Bayesian information criterion (BIC), see [21] , values.
distribution and compare it with the other fitted distributions like a flexible Weibull extension (FWE) distribution, Weibull (W) distribution, linear failure rate (LFR) distribution, Exponentiated Weibull (EW) distribution, generalized linear failure rate (GLFR) distribution and Exponentiated Flexible Weibull (EFW) distribution by using Kolmogorov Smirnov (K-S) statistic, P-value, Akaike information criterion (AIC), as well as Akaike Information Criterion with correction (AICC), see [20] and also Bayesian information criterion (BIC), see [21] , values.
Table 3 gives the maximum likelihood estimations of parameters for EFWE distribution, the value of K-S Statistics and P-value. As well the values of the log-likelihood functions, AIC, AICC and BIC are in Table 4.
From Table 3 and Table 4 we note that the EFWE distribution with three parameters gives a better fit than the previous models distributions. It has the largest log-likelihood
![]()
Table 2. Life time of 50 devices, see Aarset [22] .
![]()
Table 3. The maximum likelihood estimations and K-S of parameters for Aarset data [22] .
![]()
Table 4. The log-likelihood function, AIC, AICC and BIC values of distributions for Aarset data [22] .
![]()
Figure 7. Profile of the log-likelihood for![]() .
.
function, and also P-value, on the other hand the smallest K-S, AIC, AICC and BIC values from among those considered in this article.
Substituting the maximum likelihood estimations of the unknown parameters ![]() and
and ![]() into Equation (35), we have the estimation of the variance covariance matrix as follows
into Equation (35), we have the estimation of the variance covariance matrix as follows
![]()
The approximate 95% two sided confidence intervals of the unknown parameters ![]() and
and ![]() are
are![]() ,
, ![]() and
and![]() , respectively.
, respectively.
From, Figure 7 and Figure 8 we note that the likelihood function have unique solution.
Figure 9 represents the estimation for the survival function![]() , by using the Kaplan-Meier method and its fitted parametric estimations when the distribution is assumed to be FW, W, LFR, EW, GLFR, EFW and EFWE are computed and plotted in the following shape.
, by using the Kaplan-Meier method and its fitted parametric estimations when the distribution is assumed to be FW, W, LFR, EW, GLFR, EFW and EFWE are computed and plotted in the following shape.
Figure 10 and Figure 11 give the form of the hazard rate ![]() and cumulative distribution function for the FW, W, LFR, EW, GLFR, EFW and EFWE which are used to fit the data when the unknown parameters included in each distribution are replaced by their maximum likelihood estimation.
and cumulative distribution function for the FW, W, LFR, EW, GLFR, EFW and EFWE which are used to fit the data when the unknown parameters included in each distribution are replaced by their maximum likelihood estimation.
![]()
Figure 8. Profile of the log-likelihood for![]() .
.
![]()
Figure 9. The Kaplan-Meier estimate of the survival function ![]() for Aarset data [22] .
for Aarset data [22] .
![]()
Figure 10. Fitted hazard rate function ![]() for Aarset data [22] .
for Aarset data [22] .
![]()
Figure 11. Fitted cumulative distribution function ![]() for Aarset data [22] .
for Aarset data [22] .
8. Conclusion
We propose a new distribution, based on the exponential generalized distribution. The general idea is to add parameter to a flexible Weibull extension FWE distribution, this new distribution is called the exponential flexible Weibull extension EFWE. Its definition and some of statistical properties are studied. We use the maximum likelihood method for estimating parameters. Finally, the advantage of the EFWE distribution is concluded by an application using real data. Moreover, it is shown that the exponential flexible Weibull extension EFWE distribution fits better than existing modifications of the Weibull and flexible Weibull distributions.