1. Introduction
In the study of nonlinear science, finding the exact solution of nonlinear evolution equations is an important subject. Different methods have their different types of specific applications for nonlinear evolution equations. In recent years many scholars put forward and developed several new methods for solving PDEs which based on the original method, such as Hirota’s bilinear method [1] , homogeneous balance method [2] [3] , projective Riccati equation method [4] [5] , Jacobi elliptic functions method [6] , auxiliary equation method [7] , and separation of variables [8] [9] [10] . Among them, the tanh-coth method and the sine-cosine method are powerful and widely used in several research works. For single soliton solution, the tanh-coth method is easy to use and has been applied for a wide variety of nonlinear problems.
In the plasma physics, solid physics, fluid mechanics, etc., the Gardner equation is written as
 (1)
(1)
which is also called the KdV-mKdV equation. The model can be well described the wave propagation in a one-dimensional nonlinear lattice with a non harmonic bound particle. Gardner equations have very important application in mathematics, physics, engineering and other fields. Different types of equations can be obtained by changing the value of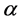 ,
,  ,
,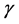 .
.
With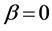 ,
,  , the KdV equation is written as
, the KdV equation is written as
 (2)
(2)
where the parameter 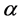 can be scaled to any real number, usually taking
can be scaled to any real number, usually taking  or
or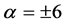 . KdV equation simulates a variety of nonlinear phenomena, including the ion acoustic waves and diving waves in the plasma.
. KdV equation simulates a variety of nonlinear phenomena, including the ion acoustic waves and diving waves in the plasma.
With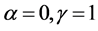 , we get the mKdV equation which is written as
, we get the mKdV equation which is written as
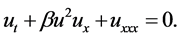 (3)
(3)
It is completely integrable [11] and can be obtained by Miura transformation of the KdV equation.
The Gardner equations are used to describe many physical models, which are closely related to the study of physics. So it is very important to study it deeply.
With , the (1 + 1)-Gardner equation turns out to be
, the (1 + 1)-Gardner equation turns out to be
 (4)
(4)
Further, the (2 + 1)-dimensional Gardner Equation [12] [13] [14] [15] is written as
 (5)
(5)
which reduces to the (1 + 1)-Gardner equation with .
.
For , Equation (5) is transformed into the KP equation as
, Equation (5) is transformed into the KP equation as
 (6)
(6)
while it is the modified KP equation with![]() . Therefore, the (2 + 1)-Gardner equation combines KP equation and modified KP equation.
. Therefore, the (2 + 1)-Gardner equation combines KP equation and modified KP equation.
With![]() , the (2 + 1)-Gardner equation turns out to be
, the (2 + 1)-Gardner equation turns out to be
![]() (7)
(7)
We had found soliton solutions, travelling wave solutions and plane periodic solutions of KdV and mKdV equations through tanh-coth method. In order to prove superiority of the tanh-coth method, we apply it on Gardner equations which are more complex and have higher dimensions.
This paper is organized as follows. In Section 2, we introduce the tanh-coth method. In Section 3, we first substitute the wave variable ![]() into the (1 + 1)-Gardner equation, and then integrate once. Based on the tanh-coth method, the soliton and kink solutions of the (1 + 1)-Gardner are given. In Section 4, we would like to search for solutions to the dimensionally reduced (2 + 1)-Gardner equation from substituting the wave variable
into the (1 + 1)-Gardner equation, and then integrate once. Based on the tanh-coth method, the soliton and kink solutions of the (1 + 1)-Gardner are given. In Section 4, we would like to search for solutions to the dimensionally reduced (2 + 1)-Gardner equation from substituting the wave variable![]() . The solutions are obtained by tanh-coth method and the soliton solution is graphically revealed. A conclusion is given in Section 5.
. The solutions are obtained by tanh-coth method and the soliton solution is graphically revealed. A conclusion is given in Section 5.
2. The tanh-coth Method
A wave variable ![]() converts any PDE
converts any PDE
![]() (8)
(8)
to an ODE
![]() (9)
(9)
Equation (9) is then integrated as long as all terms contain derivatives where integration constants are considered zeros.
Introducing an independent variable
![]() (10)
(10)
where ![]() is the wave number. The tanh-coth method admits the use of the finite expansion
is the wave number. The tanh-coth method admits the use of the finite expansion
![]() (11)
(11)
where ![]() is a positive integer, in most cases, that will be determined by balance method. And we usually balance the highest order nonlinear terms with the linear terms of highest order by using the scheme given as follows:
is a positive integer, in most cases, that will be determined by balance method. And we usually balance the highest order nonlinear terms with the linear terms of highest order by using the scheme given as follows:
![]()
![]()
![]()
![]() (12)
(12)
Substituting (11) into the reduced ODE results. We then collect all coefficients of each power of ![]() in the resulting equation where these coefficients have to vanish. This will give a system of algebraic equations involving the parameters
in the resulting equation where these coefficients have to vanish. This will give a system of algebraic equations involving the parameters ![]() and c. Finally, we obtain an analytic solution
and c. Finally, we obtain an analytic solution ![]() in a closed form.
in a closed form.
3. The Solutions of (1 + 1)-Gardner Equation
We first substitute the wave variable ![]() into the (1 + 1)-Gardner equation
into the (1 + 1)-Gardner equation
![]() (13)
(13)
that gives
![]() (14)
(14)
Integrating once to obtain
![]() (15)
(15)
We then balance the nonlinear term![]() , that has the exponent
, that has the exponent![]() , with the highest order derivative
, with the highest order derivative![]() , that has the exponent
, that has the exponent![]() . Using the balance process leads to
. Using the balance process leads to
![]() (16)
(16)
that gives
![]() (17)
(17)
The tanh-coth method allows us to use the substitution
![]() (18)
(18)
Substituting (18) into (15), collecting the coefficients of each power of![]() , setting each coefficient to zero, we find
, setting each coefficient to zero, we find
![]()
![]()
![]()
![]()
We find the following sets of solutions:
(i)![]() (19)
(19)
(ii)![]() (20)
(20)
(iii)![]() (21)
(21)
Consequently, we obtain the following solutions:
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
Following immediately. Figure 1 shows a single soliton solution ![]() for
for![]() . In the graph, the X axis is
. In the graph, the X axis is![]() , the Y axis is
, the Y axis is![]() , and the Z axis is
, and the Z axis is![]() . It can be see that the one-soliton solution is characterized by an infinite wing. This shows
. It can be see that the one-soliton solution is characterized by an infinite wing. This shows
that ![]() as
as ![]() and
and ![]() one of them tends to infinity, that is,
one of them tends to infinity, that is, ![]() tends to infinity.
tends to infinity.
![]()
Figure 1. Graph of the one-solution solution ![]() for
for ![]() characterized by an infinite wing.
characterized by an infinite wing.
4. The Solutions of (2 + 1)-Gardner Equation
We first substitute the wave variable ![]() into the (2 + 1)-Gardner equation
into the (2 + 1)-Gardner equation
![]() (25)
(25)
that gives
![]()
Based on![]() , we get
, we get
![]() (26)
(26)
Integrating once to obtain
![]() (27)
(27)
We then balance the nonlinear term![]() , that has the exponent
, that has the exponent![]() , with the highest order derivative
, with the highest order derivative![]() , that has the exponent
, that has the exponent![]() . Using the balance process leads to
. Using the balance process leads to
![]() (28)
(28)
that gives
![]() (29)
(29)
The tanh-coth method allows us to use the substitution
![]() (30)
(30)
Substituting (30) into (27), that gives
![]()
Collecting the coefficients of each power of ![]() and then setting each coefficient to zero that leads to the following set of constraining equations for the parameters:
and then setting each coefficient to zero that leads to the following set of constraining equations for the parameters:
![]()
![]()
![]()
![]()
We find the following sets of solutions:
(i)![]() (31)
(31)
(ii)![]() (32)
(32)
(iii)![]() (33)
(33)
Consequently, we obtain the solutions as
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
where ![]() and
and ![]() are kink solutions. And the kink solution’s graph is changing along with
are kink solutions. And the kink solution’s graph is changing along with ![]() taking different values.
taking different values.
Following immediately. Figure 2 below shows the one-soliton solution ![]() for
for![]() . From the graph we can see, the one-soliton solution is cha-racterized by infinite tail. This shows that
. From the graph we can see, the one-soliton solution is cha-racterized by infinite tail. This shows that ![]() as
as ![]() and
and ![]() one of them tends to infinity, that is,
one of them tends to infinity, that is, ![]() tends to infinity.
tends to infinity.
![]()
Figure 2. Graph of ![]() for
for ![]() characterized by an infinite tail.
characterized by an infinite tail.
5. Conclusion
In this paper, we obtain the soliton and kink solutions of the (1 + 1)-Gardner equation and (2 + 1)-Gardner equation through the tanh-coth method. The biggest advantage is that by traveling wave transformation, the problem of solving nonlinear partial differential equations is transformed into the problem of solving nonlinear ordinary differential equations or nonlinear algebraic equations. The tanh-coth method is convenient to use, and can be further extended to solve other nonlinear partial differential equations.
Acknowledgements
The authors would like to express their sincere thanks to the referees for their enthusiastic guidance and help. This work is supported by the National Natural Science Foundation of China (No.11371326)