1. Introduction
Thanks to its analytical tractability, the Perpetual Youth (PY) model has been extensively used by various strands of literature in economics. As it is well known, PY model is an overlapping generation model in continuous time. Just to cite some contributions, the PY framework is used for the analysis of public debt issues, as in [1] and [3] ; for assessing the interactions between social security and foreign indebtedness, as in [4] ; for the analysis of redistributive effects of public polices, such as public investments and their financing, as in [5] .
The aim of this paper is to assess the instantaneous non-human wealth distribution that characterizes the steady state equilibrium of a PY model introduced by [1] 1. For this scope, we derive a Generalized Lorenz Curve of wealth distribution at the steady state equilibrium.
Given the demographic structure underlying the PY model, in steady state older individuals owns a greater level of non-human wealth than younger individuals, while the size of the older population is smaller than the size of the younger one; thus, the state of non-human wealth distribution is uncertain.
The issue appears to be relevant in a positive analysis perspective. In fact, the inter and intragenerational welfare evaluation could justify an economic policy, yet the same economic policy could deeply influence the present distribution and, in a Political economics perspective, the behavior of living voters.
In Section 2, I introduce a basic model of PY. In Section 3, a Generalized Lorenz Curve for the state equilibrium of the model is derived. In Section 4, some comparative statics exercises are presented. Section 5 concludes.
2. The Perpetual Youth Framework
In this section I briefly present the basic version of the PY model proposed by [1] . I focus on simple functional forms, abstract from endogenous growth and congestion, and assume exogenous labor supply. A small open economy is populated by individuals who differs for their date of birth j. The total mass of the population is 1. In each period t any individual faces an age-independent probability of death p. This amounts to assume that for each individual the random variable “time until death at time t” is exponentially distributed with parameter p.
A representative agent born at time j < t will decide her consumption path by maximizing the following intertemporal expected utility function:
 (1)
(1)
subject to
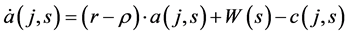 (2)
(2)
 (3)
(3)
where a(j, s) is the stock of non-human wealth accumulated by the representative agent belonging to generation j, from her birth to time s. W(s) is the gross wage. To the sake of simplicity we have taken logarithmic utility function.
Financial assets can be either domestic (V(s)) or foreign (F(s)), and at the aggregate level we have that . The interest rate r is fixed to the international level, since we assume a small open economy.
. The interest rate r is fixed to the international level, since we assume a small open economy.
From the FOCs of the consumer decision problem we get the following Euler equation:
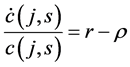 (4)
(4)
while the consumption function will be:
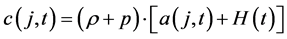 (5)
(5)
where 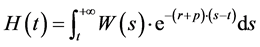 is the stock of human wealth at time t.
is the stock of human wealth at time t.
A well known property of the PY model is that in steady state we have to assume 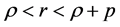 in order to get well defined solutions at aggregate level2.
in order to get well defined solutions at aggregate level2.
3. Instantaneous Wealth Distribution in a PY Model
The aim of this section is to determine the instantaneous distribution of wealth at the steady state equilibrium and taking into account the demographic structure induced by the PY framework. To this purpose we will derive a Generalized Lorenz Curve3. We will carry on this task in five steps.
1) First of all we have to compute the amount of individual financial wealth. Starting from the Euler equation describing the equilibrium path of individual consumption and exploiting the assumption that the economy has been always in its steady state equilibrium, we get individual consumption at a given time s:
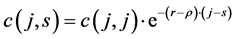 (6)
(6)
where, since the individual does not own any financial wealth at her birth, we have that  where
where 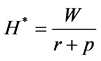 is the steady state level of human wealth.
is the steady state level of human wealth.
Substituting into the individual dynamic budget constraint we get:
 (7)
(7)
Solving the differential Equation (7) we get the steady state level of individual stock of non-human wealth at time t of a consumer belonging to generation j:
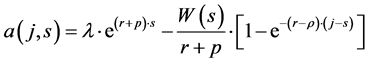 (8)
(8)
where λ is a constant that can be determined using the initial condition a(j, j) = 0, that is:
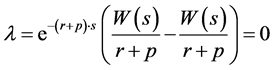 (9)
(9)
The final expression for the steady state amount for individual non-human wealth is:
 (10)
(10)
Before concluding this step it is necessary to check that Equation (10) matches some conditions. The amount of non-human wealth should be always non-negative: this condition is matched since j < s implies that ; therefore, a(j, s) is always positive.
; therefore, a(j, s) is always positive.
The amount of non-human wealth should increase with age, that is the first derivative of (10) with respect to j should be negative:
 (11)
(11)
the derivative (11) is negative since r > ρ by assumption.
2) The aim of this step is to rewrite the (10) and the number of individuals belonging to the generation j in terms of age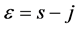 :
:
![]() (12)
(12)
and
![]() (13)
(13)
3) Now, let us determine the age distribution of the financial wealth![]() , that is given by multiplying the stock of financial wealth owned by the representative individual of age ε by the number of individuals belonging to that generation:
, that is given by multiplying the stock of financial wealth owned by the representative individual of age ε by the number of individuals belonging to that generation:
![]() (14)
(14)
In other terms Equation (14) gives the aggregate amount of non-human wealth owned by the population aged ε at time s.
4) The aim of this step is to compute the cumulative distribution of non-human wealth in the age interval (0, E). This can be obtained by integrating on such interval the function Γ:
![]() (15)
(15)
5) Now, we have all what we need to build a Generalized Lorenz Curve. In order to take this step we have to sort living individuals according to their amount of non- human wealth from the poorest to the richest. As far r > ρ, we can note that in the PY model, sorting individuals according to financial wealth amounts to sorting them according to age. Therefore, it will be useful to switch from the variable E to the variable f, where f indicates the f% poorest individuals of the population. Since the age distribution of the population is exponential we have that
![]() . Substituting the latter into Equation (8) we get the expression for the Generalized Lorenz curve:
. Substituting the latter into Equation (8) we get the expression for the Generalized Lorenz curve:
![]() (16)
(16)
where![]() ,
, ![]() , and
, and![]() .
.
4. Comparative Statics
Let us now assess how non-human wealth inequality is affected by changes in two important variables, that is the interest rate r and the rate of population turnover p (i.e. the life expectancy 1/p).
The first partial derivative of (16) with respect to r is:
![]() (17)
(17)
where![]() . Under the assumptions on the parameter and reminding
. Under the assumptions on the parameter and reminding
that![]() , this derivative is always positive4. This means that if we compare two economies A and B such that (rB > rA), then at the steady state, economy B exhibits a lower degree of non-human wealth inequality than economy A. This situation is shown in Figure 1, where A (B) represents the Generalized Lorenz curve with interest rate rA(rB).The intuition behind this result is that, caeter is paribus, with a higher interest rates the accumulation of non-human wealth is faster; in a PY model this implies that, at time s younger individuals will hold a higher share of total financial wealth; since younger individuals are also poorer relative to older ones, this leads to lower concentration of non-human wealth.
, this derivative is always positive4. This means that if we compare two economies A and B such that (rB > rA), then at the steady state, economy B exhibits a lower degree of non-human wealth inequality than economy A. This situation is shown in Figure 1, where A (B) represents the Generalized Lorenz curve with interest rate rA(rB).The intuition behind this result is that, caeter is paribus, with a higher interest rates the accumulation of non-human wealth is faster; in a PY model this implies that, at time s younger individuals will hold a higher share of total financial wealth; since younger individuals are also poorer relative to older ones, this leads to lower concentration of non-human wealth.
This result is interesting in three respects. First, relative to the effects of monetary policy: if we are willing to accept the story told by PY model, steady state equilibria characterized by higher interest rates will lead to higher non-human wealth inequality. Second, relative to capital income taxation: in a small open economy, as long as the residence principle is applied in capital income taxation, higher tax rates implies―at the steady state―lower financial wealth concentration. Third, the fact that at the steady state, lower interest rates are associated with higher non-human wealth inequality seems to be another theoretical argument in support to the historical evidence presented
![]()
Figure 1. Generalized Lorenz curve for alternative parameters.
by [8] , given that the US are experiencing a very long trend of low interest rates associated with high wealth inequality.
The effect of a change in p is given by the first derivative of Equation (16):
![]() (18)
(18)
under the assumptions on the parameter this derivatives is always negative5.
This means that if we compare two economies A and B, that differ just for their population turnover rate, let us assume (pA > pB) then we will have that economy B in steady state will be characterized by a higher degree of non-human wealth inequality compared with economy A: in the economy where the turnover rate is lower (i.e. economy B), elderly population is a higher share of total population; this means that the owners of a higher share of financial wealth represent a higher share of the population relative to the economy A and the degree of inequality will be lower.
5. Conclusion
In this paper, I have derived the Generalized Lorenz curve of financial wealth distribution in the steady state equilibrium of a Perpetual Youth model. To the best of my knowledge, this kind of contribution is so far absent in economic literature. This contributes to the assessment of the effects of monetary and fiscal policy on financial wealth concentration across cohorts. I find that, at the steady state equilibrium: i) an increase in (after tax) interest rates increases financial wealth concentration; ii) economies with a higher population turnover rates exhibit lower financial wealth concentration.
NOTES
![]()
1As it is well known the seminal contribution that proposed a Ramsey model with agents facing a finite time horizon tracks back to [2] .
![]()
2See [1] and [6] .
3For a definition of Generalized Lorenz Curve see [7] . The object that we derive is a Generalized Lorenz Curve and not an ordinary Lorenz Curve because of the total population has mass 1.
![]()
4Simulations that support this result are available at the following link: http://antoniosciala.jimdo.com/research/?logout=1.
![]()
5Simulations that support this result are available at the following link: http://antoniosciala.jimdo.com/research/?logout=1.