Solution of Nonlinear Advection-Diffusion Equations via Linear Fractional Map Type Nonlinear QCA ()
1. Introduction
Quantum Cellular Automaton (QCA) [1] is a quantum version of (classical) cellular automaton (CA). The word QCA was introduced by Grössing and Zeilinger [2] . But their model was not completely unitary. The QCA in the right meaning which has both locality and unitarity, was firstly investigated by Meyer [3] [4] [5] [6] , then followed by Boghosian and Taylor [7] [8] , although they used the term Quantum lattice gas automata (QLGA) for the two-component case. Since the middle of the 2000s, new axiomatic approaches of QCA different from previous conventional or ad hoc ones have been proposed by several researchers [9] [10] [11] in order to comprehend QCA in more systematic and unified way by clarifying the definitions and/or to cope with the difficulties for extending it in a form relevant to the infinite dimensional Hilbert space. In most axiomatic QCAs, the unitarity and the causality (namely the existence of the upper limit on the speed of the information propagation) are fundamental and the locality is derived from them [10] . In this study, however, we describe QCA in a rather conventional fashion. There are several frameworks for quantum lattice systems other than QCA, namely Quantum Walk (QW) [12] , Quantum Lattice Gas Automata (QLGA) [7] [8] and Quantum Lattice Boltzmann (QLB) [13] . They are similar or mathematically equivalent to some QCAs [14] [15] [16] .
Consider the simplest partitioned QCA on a 1D-time 1D-space lattice of which time evolution rule is given by Figure 1 and Equation (1). This rule is governed by the 2 × 2 basic unitary matrix (which is called scattering unitary matrix [11] ) which operates on a vector consisting of functions at adjacent grid points.
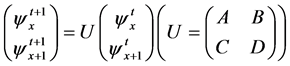 (1)
(1)
The simplest is the QCA with constant U (independent from space and time). We then generalize it to the QCA with space dependent U as described by Equation (2).
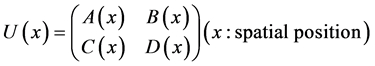 (2)
(2)
Moreover QCA/QW with time dependent  has been studied. Especially remarkable results are obtained for the QW of which parameter is given by Fibonacci sequence [17] [18] . In this paper we propose a non-linear QCA (NLQCA) and investigate its properties. The basic 2 × 2 matrix is given by
has been studied. Especially remarkable results are obtained for the QW of which parameter is given by Fibonacci sequence [17] [18] . In this paper we propose a non-linear QCA (NLQCA) and investigate its properties. The basic 2 × 2 matrix is given by
![]()
Figure 1. Evolution rule of QCA: the unit system where grid spacing 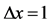 and time step
and time step 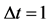 is used.
is used.
 (3)
(3)
In the NLQCA the basic 2 × 2 matrix depends on the amplitude of wave function. QCA’s fundamental and powerful properties are unitarity, locality, reversibility, and when we construct NLQCA, it is important to keep these properties. NLQCA was investigated by Meyer [19] in a rather general way. And several articles [20] [21] can be found especially in the name of nonlinear quantum walk (NLQW). However it seems that the concrete form of NLQCA has not been presented for the study. We here propose linear fractional map type (LFMT) nonlinear QCA (NLQCA) and study its properties in order to clearly understand NLQCA.
After this introduction, the rest of the article is organized as follows. In Section 2 we introduce LFMT phase rotation and define three typical types of it, type-0, type-1 and type-2. We also perform its fixed point analysis, which is a useful mean to investigate the characteristics of NLQCA. In Section 3 we introduce two kinds of reversible NLQCA using LFMT phase rotation, namely complex-LFMT NLQCA and real-LFMT NLQCA. In Section 4 we investigate the property of complex-LFMT NLQCA focusing on type-0. In Section 5 and 6 we investigate the property of real-LFMT NLQCA (type-0 in Section 5 and type-2 in Section 6).
2. Linear Fractional Map Type Phase Rotation
2.1. Definition
Consider the following map (complex plane to the complex plane itself) which conserves its absolute value.
 (4)
(4)
or
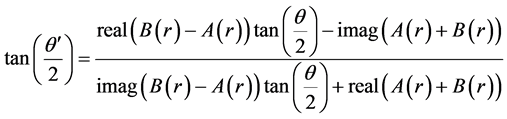 (5)
(5)
Here  are complex numbers and functions of
are complex numbers and functions of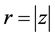 .
. 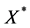 denotes the complex conjugate of X. As the numerator and the denominator of Equation (4) are complex conjugate with each other, the absolute value of Equation (4) is 1. Therefore Equation (4) represents a phase rotation map. The equivalence of Equations (4) and (5) is proved easily as follows. From Equation (5)
denotes the complex conjugate of X. As the numerator and the denominator of Equation (4) are complex conjugate with each other, the absolute value of Equation (4) is 1. Therefore Equation (4) represents a phase rotation map. The equivalence of Equations (4) and (5) is proved easily as follows. From Equation (5)
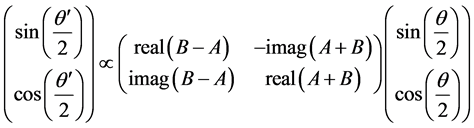 (6)
(6)
Then
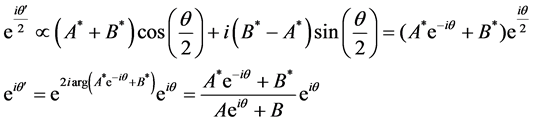 (7)
(7)
It is easily shown that LFMT phase rotations are closed with respect to inversion and composition. (see Equations (44) and (55) in Appendix A)
Generally A, B can be any function of r. However we restrict our discussion to the following 3 cases for simplicity. We discuss type-0 mainly in this study.
(1) type-0 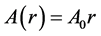
(2) type-1 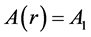
(3) type-2 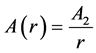
Here,  are constant complex numbers, and we assume
are constant complex numbers, and we assume ![]() is constant for all cases. There are several formulas on LFMT phase rotations, and we will summarize them in appendix A. We also summarize the extension of this discrete phase rotation to the continuous one in appendix B. Additionally, we use the following notation for simplicity.
is constant for all cases. There are several formulas on LFMT phase rotations, and we will summarize them in appendix A. We also summarize the extension of this discrete phase rotation to the continuous one in appendix B. Additionally, we use the following notation for simplicity.
[Definition]
![]() denotes the function
denotes the function![]() .
.
![]() denotes
denotes ![]() (namely the phase rotation of the double angle of the argument).
(namely the phase rotation of the double angle of the argument).
For example, by using the above definitions, ![]() is simplified
is simplified
as ![]() or
or![]() .
.
The function which multiplies the constant k is written as [k]. Note that $ is not included in [] in this case. Complex conjugate operator C, inversion operator V are defined as
![]() (8)
(8)
respectively. We will omit the function composition symbol ![]() when [..] are uses.
when [..] are uses.
2.2. Small Amplitude Limit and Large Amplitude Limit
In LFMT phase rotation (type-0)
![]() (9)
(9)
![]() corresponds to small or large amplitude region respectively.
corresponds to small or large amplitude region respectively.
In small amplitude region this map becomes a linear map ![]() and in large amplitude region, this becomes a linear map with complex conjugation
and in large amplitude region, this becomes a linear map with complex conjugation![]()
![]() . In Figure 2, we illustrate LFMT phase rotation in the case of A = B = 1. We
. In Figure 2, we illustrate LFMT phase rotation in the case of A = B = 1. We
can see that this map closes to a linear map at the limits of![]() .
.
2.3. Fixed Points and Their Stability
Approaches from fixed point analysis are useful when we investigate the characteristics of complex-LFMT NLQCA. In general a map from a circle to the circle itself is called a circle map. LFMT phase rotation of Equation (4) is a circle map for any fixed r. Now we find fixed points of this circle map. The equation for the fixed points is
![]() (10)
(10)
Apparently the Equation (10) is satisfied when![]() , Namely
, Namely
![]() (11)
(11)
Therefore, Equation (11) has a real solution ![]() if and only if
if and only if![]() . In order to investigate the stability of these fixed points, we calculate the gain of the linearized map around the fixed point
. In order to investigate the stability of these fixed points, we calculate the gain of the linearized map around the fixed point![]() . Let x be the small angle deviation from
. Let x be the small angle deviation from![]() , then we obtain the linearized map as follows.
, then we obtain the linearized map as follows.
![]() (12)
(12)
This means the phase gain at the fixed point ![]() is
is
![]()
Figure 2. Type-0 LFMT phase rotation in the case of A = B = 1. Polar coordinates before/after the mapping are shown. Left: before the mapping, Center: after the mapping (small amplitude region), Right: after the mapping (large amplitude region).
![]() (13)
(13)
The 2nd equation in the parentheses of Equation (13) is obtained by using Equation (11). If ![]() is a fixed point then
is a fixed point then ![]() is another fixed point and it can be proved that the product of the gains for these two fixed points is 1 as shown in Equation (14).
is another fixed point and it can be proved that the product of the gains for these two fixed points is 1 as shown in Equation (14).
![]() (14)
(14)
because the product of the two denominators is
![]()
Therefore one fixed point is stable and the other fixed point is unstable ![]() or both fixed points are critical (marginally stable/unstable)
or both fixed points are critical (marginally stable/unstable)![]() . From Equation (13), the critical situation means
. From Equation (13), the critical situation means![]() , namely
, namely ![]() or
or ![]()
![]() . Moreover, from (11) we can see that
. Moreover, from (11) we can see that ![]() in the case
in the case ![]() and
and ![]() in the case
in the case![]() .
. ![]() is merely the lower bound of the condition for a critical point to exist
is merely the lower bound of the condition for a critical point to exist ![]()
3. LFMT NLQCA
In this study, we investigate two kinds of NLQCA using LFMT phase rotation. The one is complex-LFMT NLQCA and the other is real-LFMT NLQCA. We refer the Time Dependent Schrödinger Equation (TDSE)-type QCA [22] with additional LFMT phase rotation at each grid point as complex-LFMT NLQCA. And we refer the NLQCA whose basic 2 × 2 unitary matrix (in the sense of Equation (3)) is given by the mapping of real and imaginal part of LFMT phase rotation as real-LFMT NLQCA.
4. Property of Type-0 Complex-LFMT NLQCA
In complex-LFMT NLQCA, the 2 × 2 unitary matrix ![]() of linear TDSE- type QCA (see [22] ) and the nonlinear LFMT phase rotation are applied alternatively.
of linear TDSE- type QCA (see [22] ) and the nonlinear LFMT phase rotation are applied alternatively.
In the above expression ![]() is the x-component of Pauli matrices and
is the x-component of Pauli matrices and![]() . In this study, we perform the numerical experiment with
. In this study, we perform the numerical experiment with ![]()
and vary the phase of B. (As the change of the phase of A can be compensated by that of initial value of![]() , we need not vary the phase of A when we investigate merely the qualitative behavior of the time evolution not sensitive to the initial
, we need not vary the phase of A when we investigate merely the qualitative behavior of the time evolution not sensitive to the initial![]() , therefore we set A = 1.) The obtained qualitative behavior of complex-LFMT NLQCA can be summarizes as follows. Before showing the summary of the simulation, we firstly illustrate the region for parameters A, B where a phase lock can occur in Figure 3, which is the key diagram to understand the qualitative behavior. |B| is assumed to be 1 without loss of generality. The unit of horizontal axis is
, therefore we set A = 1.) The obtained qualitative behavior of complex-LFMT NLQCA can be summarizes as follows. Before showing the summary of the simulation, we firstly illustrate the region for parameters A, B where a phase lock can occur in Figure 3, which is the key diagram to understand the qualitative behavior. |B| is assumed to be 1 without loss of generality. The unit of horizontal axis is![]() . The region
. The region ![]() (where a fixed point can exist) is colored blue, although the neighbor of pure imaginal B (namely 0.25, 0.75 in horizontal axis) is left white because both of their fixed points are marginally stable/unstable.
(where a fixed point can exist) is colored blue, although the neighbor of pure imaginal B (namely 0.25, 0.75 in horizontal axis) is left white because both of their fixed points are marginally stable/unstable.
In type-0 LFMT NLQCA, a singular amplitude point exists where![]() . We work on the domain far from such singularity, namely
. We work on the domain far from such singularity, namely ![]() (small amplitude case) and
(small amplitude case) and ![]() (large amplitude case) in all space and time. We discuss here only small amplitude case. Qualitative behavior is roughly classified by the occurrence of a phase lock.
(large amplitude case) in all space and time. We discuss here only small amplitude case. Qualitative behavior is roughly classified by the occurrence of a phase lock.
(Case 1) when imag(B) = 0 [000 in Figure 4]:
Phase lock occurs in all space and the waveform reaches a flat pattern at the end.
(Case 2) when imag(B) is sufficiently small but not 0 [001,999 in Figure 4]:
According to the magnitude relation between![]() , a phase lock or an unlock occurs temporally or spatially. The noise from spatial high frequency is rather low, and the waveform is smooth.
, a phase lock or an unlock occurs temporally or spatially. The noise from spatial high frequency is rather low, and the waveform is smooth.
(Case 3) when imag(B) is not small [050,075,100,900,925,950 in Figure 4]:
A phase lock never occurs, and the phase is always rotating.
In Figure 4 we show the snapshots of the waveform at t = 2000. The parameter of the
linear QCA part is![]() , and the parameters of nonlinear phase rotation part are A = 1, |B| = 1 and the arg (B) is varied as
, and the parameters of nonlinear phase rotation part are A = 1, |B| = 1 and the arg (B) is varied as![]() .
.
![]()
Figure 3. The region for parameters A, B where a phase lock can occur (which depends on the amplitude level![]() ).
).
The 3-digit number DDD in the legend indicates that![]() . Periodic boundary condition is used. At t = 0,
. Periodic boundary condition is used. At t = 0, ![]() is set. Absolute value of two-point averaged
is set. Absolute value of two-point averaged ![]() are plotted
are plotted
![]() .
.
When arg(B) = 0 (Case 0), the perfect phase lock occurs. At ![]()
(Case 2), the waveform behaves like an attractive Nonlinear Schrödinger Equation(NLS) (namely it does not diffuse as in free TDSE case) and condensates with a vibration. At
![]() (Case 2), the waveform behaves like a repulsive NLS (namely it
(Case 2), the waveform behaves like a repulsive NLS (namely it
diffuses faster than in free TDSE case). As arg(B) goes away from 0 (Case 3), the waveform behaves like a free TDSE (see 050,075,100,900,925,950) probably because only the time averaged phase rotation speed is mainly effective to the qualitative behavior. Here we
mean NLS by the equation i![]() .
.
However even in the parameter region of Case 3, singular behaviors are observed at the neighbor of some special parameters which depend also on ![]() (the parameter of the linear QCA part). Especially, there is a singular point at
(the parameter of the linear QCA part). Especially, there is a singular point at
![]() (15)
(15)
And above this point (namely![]() ) the behavior is significantly different from that of free TDSE. The observation of this phenomena is shown in Figure 5 in
) the behavior is significantly different from that of free TDSE. The observation of this phenomena is shown in Figure 5 in
the case of![]() . Moreover other singular points are observed at
. Moreover other singular points are observed at
![]() (16)
(16)
Above these points, the noise level with reference to free TDSE becomes larger. In
Figure 5 periodic boundary condition is used. When ![]()
the behavior is perfectly same as free TDSE(see 299) and when it exceed this point, the deviation from the free TDSE occurs (see 300,301,304) and the deviation becomes smaller as arg(B) goes away from the point (see 306,310). In the lower graph (t = 14500) of Figure 5, waveforms of 299,306,310 are almost the same as the initial Gaussian wave-form with a half period’s shift, which is a prominent characteristic of free TDSE. (In general, Hamiltonian all eigenvalue differences of which has a finite common divisor, has temporal periodicity. In free TDSE case, the energy spectrum has the form ![]() and has the periodicity time T, and moreover has the pseudo periodicity time T/2. At t = T/2, only the n = odd components change their sign, which means the half spatial period’s shift of any initial waveform.) Note that with respect to free TDSE t = 2750
and has the periodicity time T, and moreover has the pseudo periodicity time T/2. At t = T/2, only the n = odd components change their sign, which means the half spatial period’s shift of any initial waveform.) Note that with respect to free TDSE t = 2750
of Figure 5 ![]() approximately corresponds to t = 2000 of Figure 4
approximately corresponds to t = 2000 of Figure 4![]() ,
,
because![]() . We need further investigation on the state
. We need further investigation on the state
and the mechanism of these singularities.
5. Property of Type-0 Real-LFMT NLQCA
5.1. Parameters for the Numerical Experiment
From this section we investigate real-LFMT NLQCA. Firstly we explain the parameters A, B we use in the case of type-0 described by Equation (17).
![]() (17)
(17)
As![]() , we have only to investigate 32 out of 64 (= 8 × 8) parameter sets, and moreover about a half of those 32 is sufficient if we employ the space reflection symmetry (P) which we explain next.
, we have only to investigate 32 out of 64 (= 8 × 8) parameter sets, and moreover about a half of those 32 is sufficient if we employ the space reflection symmetry (P) which we explain next.
5.2. Symmetry and Classification
We consider the following CPTA symmetry (Equations (18)-(21)). We find that the NLQCAs with a parameter which belongs to the same parameter groups behave qualitatively similarly.
・ C-inversion (see Equations (45) and (46) in Appendix A)
![]() (18)
(18)
・ P-inversion (see Equations (45) and (46) in Appendix A)
![]() (19)
(19)
(Note that![]() , namely [i] C means P-inversion which swaps a and b.)
, namely [i] C means P-inversion which swaps a and b.)
・ T-inversion (see Equation (44) in Appendix A)
![]() (20)
(20)
・ A-inversion (see Equation (45) in Appendix A)
![]() (21)
(21)
These C, P, T, A have the following properties.
(1) ![]() (namely involution)
(namely involution)
(2) A commutes with P, T, C
(3) P commutes with T (PT = TP)
(4) C “anti”-commute with T, P (CP = PCA, CT = TCA)
We define the 6 groups C, D, E, F, G, H so that ID1 and ID2 belongs to the same group if ID1 and ID2 can be transformed each other by C, P, T, A. IDs that belongs to the same group have qualitatively similar behaviors.
[Remark]
These symmetry formulas are same for the type-2, because A, B can be regarded as function of |$| and we can replace A with ![]() in Equations (18)-(21).
in Equations (18)-(21).
The CPTA mapping for ID = (n, m) of Equation (17) is shown in Table 1.
![]()
Table 1. Mapping table for ID = (n, m) by applying P, T, A, C or their combinations.
As illustrated in Figure 6, C-inversion is simply a redefinition of the sign of the amplitudes. A-inversion is also redefinition of the sign (in this case sign inversion of the all amplitudes).
5.3. Type-G (50/10), Type-E (70), Type-C (60)
In this section we show simulated waveform of type-G/E/C. For these cases, evolution of the waveform can be explained almost by comparing to the corresponding continuous time counterpart equation we discuss later. In Figure 7 and Figure 8 the simulated waveforms of type-G are shown. In Figure 9 the simulated waveform of type-E is shown. In Figure 10 the simulated waveform of type-C is shown. In all cases initial (t =
0) waveform is set to the Gaussian form ![]() and
and
simulated both in forward time (blue) and backward time (red) with a periodic boundary condition. Backward time evolution is performed using T-inversion formula (20).
Two-point-averaged ![]() are plotted
are plotted ![]() and the spatial axis indicates
and the spatial axis indicates![]() .
.
Type-G (Figure 7) corresponds to the in viscid Burgers equation, where T-inversion simply corresponds to the inversion of moving direction. After the steep slope collapses, the NLQCA waveform goes out of the applicable range of in viscid Burgers equation approximation and KdV’s soliton-like wave packets spawn (see Figure 8).
In type-E (Figure 9) we can observe very slow diffusive behavior. This can be approximated by the certain kind of non-linear diffusion equation which we discuss later. In backward time simulation the sign of the amplitude is inverted at the beginning then behaves as a non-linear diffusion equation. This initial amplitude inversion behavior can be interpreted as the transition process from the non-positive diffusion constant to the positive one.
![]()
![]()
Figure 7. Simulation of type-G (ID = 50) (upper) and type-G (ID = 10) (lower) ![]() (inviscid Burgers equation).
(inviscid Burgers equation).
![]()
Figure 8. Simulation of type-G (ID = 50) (t = 10000 to 14000) (KdV’s soliton-like behavior).
![]()
Figure 9. Simulation of type-E (ID = 70) ![]() (nonlinear diffusion equation: porous-medium equation with the degree of porosity
(nonlinear diffusion equation: porous-medium equation with the degree of porosity![]() ).
).
Type-C (Figure 10) lies between type-G and type-E and behaves like a Burgers equation with viscosity, namely the steep slope does not collapse and keeps on moving with lowering its height. In backward time simulation the sign of the amplitude is inverted at the beginning as in type-E then behaves like a viscid Burgers equation.
5.4. Type-H (51), Type-F (71), Type-D (61)
In this section we show that type-F and type-H can be understood from the view point of fixed point. In the case of real-LMFT NLQCA the meaning of a fixed point is slightly different from that in the case of complex-LMFT NLQCA we discussed before. In this case, a fixed point waveform does not keep still but propagates to ±45 deg. direction in the spacetime. Now we consider the (pseudo) fixed point equation for a fixed waveform moving to the left or right at the speed of one. Namely
![]() (22)
(22)
or equivalently using![]() ,
,
![]() (23)
(23)
Here ![]() means a true fixed point or a pseudo fixed point respectively, and “pseudo” means accepting temporal sign alternation.
means a true fixed point or a pseudo fixed point respectively, and “pseudo” means accepting temporal sign alternation.
As
![]()
(from Equations (45) (46) (48) in Appendix A), Equation (23) can be rewritten as
![]() (24)
(24)
Obviously, in order for z to be a true fixed point or a pseudo fixed point, ![]() must be
must be
![]() (25a)
(25a)
![]() (25b)
(25b)
where R, I denotes the set of real numbers and the set of pure imaginary numbers respectively. Sufficient (and presumably necessary) conditions for Equation (25) are
![]() (26a)
(26a)
![]() (26b)
(26b)
Namely, using Equation (24)
![]() (27a)
(27a)
![]() (27b)
(27b)
From Equation (17) and Table 1, we conclude that type-F has true fixed points, and type-H has pseudo fixed points.
In Figure 11, Figure 12, Figure 13, simulated waveforms of type-H, type-F, type-D are shown respectively. In all cases initial (t = 0) waveform is set to the Gaussian form
![]() and simulated both in forward time (blue)
and simulated both in forward time (blue)
and backward time (red) with a periodic boundary condition. Backward time evolution is performed using T-inversion formula (20). Two-point-averaged ![]() are plotted
are plotted
![]() and the spatial axis indicates x/2. In all cases
and the spatial axis indicates x/2. In all cases
waveforms around the start time![]() , after a short time (t = 9900 to 10100) and after a long time (t = 499900 to 500100) are shown. Type-H (Figure 11) is half stable and Type-F (Figure 12) is super-stable and Type-D (Figure 13) is unstable. These results correspond to the above fixed point analysis. In these simulations we used
, after a short time (t = 9900 to 10100) and after a long time (t = 499900 to 500100) are shown. Type-H (Figure 11) is half stable and Type-F (Figure 12) is super-stable and Type-D (Figure 13) is unstable. These results correspond to the above fixed point analysis. In these simulations we used
the NLQCA parameter ![]() in all cases therefore in the small amplitude limit
in all cases therefore in the small amplitude limit ![]() the phase rotation becomes
the phase rotation becomes![]() . This corresponds to the
. This corresponds to the
advection type linear QCA with advection speed ![]() where the time evolution of the waveform is described as the superposition of the left-moving and right- moving wave packets (see [22] ). In this case
where the time evolution of the waveform is described as the superposition of the left-moving and right- moving wave packets (see [22] ). In this case![]() ,
,
![]() component moves right with temporal sign alternation, and
component moves right with temporal sign alternation, and ![]() component moves left with a constant sign. (
component moves left with a constant sign. (![]() corresponds to
corresponds to ![]() and
and ![]() corresponds to
corresponds to ![]() in Equation (27) respectively.)
in Equation (27) respectively.)
In type-H (Figure 11) two mountain-shaped wave packets move to opposite directions. The right-moving wave packet (which corresponds to the pseudo fixed point) is stable forever whereas the left-moving wave packet becomes unstable in the long run. Here only the waveforms for even t are plotted, therefore the temporal sign alternation of the right-moving wave packet cannot be seen. In type-F (Figure 12) the right-mov- ing wave packet disappears soon whereas the left-moving wave packet (which corresponds to the true fixed point) is super-stable. In type-D (Figure 13) the waveform is similar to type-F, namely the right-moving wave packet disappears soon whereas the left-moving wave packet keeps moving. However this left-moving wave packet becomes unstable in the long run.
5.5. Continuum Limit of Type-0 Real-LFMT NLQCA
It is known that the continuum limit of the simplest QCA becomes linear advection equation or TDSE (see for example [22] ). We find that in the case of type-0 real-LFMT NLQCA the continuum limit becomes a nonlinear advection-diffusion equation. Concretely, in type-0 real-LFMT NLQCA![]() , the continuum limit exists if B is real. Consider the case where the velocity
, the continuum limit exists if B is real. Consider the case where the velocity ![]() depends on the amplitudes (a, b, c, d) in the advection type QCA (see for example [22] ).
depends on the amplitudes (a, b, c, d) in the advection type QCA (see for example [22] ).
![]() (28)
(28)
As ![]() is the average of the amplitude and
is the average of the amplitude and ![]() is the difference
is the difference
between the right side average and the left side average, p and (q/2) means the coeffi-
cients of ψ and ![]() in
in![]() . Let
. Let ![]() be
be ![]() respectively then we have
respectively then we have
![]() (29)
(29)
By inserting Equation (28) to Equation (29) we have
![]() (30)
(30)
Therefore
![]() (31)
(31)
As Equation (31) implies that![]() , we thus obtain the type-0 real- LFMT NLQCA
, we thus obtain the type-0 real- LFMT NLQCA
![]() (32)
(32)
As NLQCA is unitary, its continuum limit must be unitary time evolution equation. The best candidate is
![]() (33)
(33)
Note that the operators ![]() are anti-Hermite.
are anti-Hermite.
Equation (33) can also be rewritten in the following forms.
![]() (34)
(34)
or if we set ![]()
![]() (35)
(35)
This implies ![]() is a conserved quantity. We can regard this equation as nonlinear advection diffusion equation of which advection coefficient and diffusion coefficient are proportional to
is a conserved quantity. We can regard this equation as nonlinear advection diffusion equation of which advection coefficient and diffusion coefficient are proportional to![]() . When p = 0 this type of nonlinear diffusion equation is called as a porous-medium equation [21] [23] . (In this case for Equation (35) the degree of the
. When p = 0 this type of nonlinear diffusion equation is called as a porous-medium equation [21] [23] . (In this case for Equation (35) the degree of the
porosity![]() ). In the article [21] a certain kind of NLQW was proposed and it was
). In the article [21] a certain kind of NLQW was proposed and it was
shown numerically that its continuum limit obeys a porous-medium equation with the degree of the porosity approximately 1.5.
In Figure 14, we demonstrate using numerical simulation that the continuum limit of NLQCA of Equation (32) is indeed well described by Equation (33). The PDE (33) is solved using Finite Difference Method (FDM) (Runge-Kutta (4th order)). Real PDE parameters ![]() are taken from A using Equation (32).
are taken from A using Equation (32).
6. Property of Type-2 Real-LFMT NLQCA
6.1. Relation to TDSE-Type Linear QCA
Type-2 real-LFMT NLQCA is related to type-0 real-LFMT NLQCA with a space inversion (see Equation (48) in Appendix A) and the basic 2 × 2 matrix of type-2 real LFMT NLACA becomes the form of Equation (36) in small amplitude limit.
![]() (36)
(36)
The linear QCA governed by Equation (36) is related to the TDSE-type linear QCA of which basic 2 × 2 matrix is given by Equation (37).
![]() (37)
(37)
Both linear QCAs (Equations (36) and (37)) have essentially the same dispersion relation Equation (38) and basically behave as TDSE [22] .
![]() (38)
(38)
Note that according to the argument in [22] , the 2 × 2 unitary matrices in the Z- transformation representation for Equations (36) and (37) are
![]() (39)
(39)
And the eigenvalues of ![]() and
and ![]() have essentially the same value except the constant phase factor, which leads to Equation (38). However in the
have essentially the same value except the constant phase factor, which leads to Equation (38). However in the ![]() limit,
limit,
eigenvectors of ![]() are
are![]() , whereas eigenvectors of
, whereas eigenvectors of ![]() are
are![]() . Therefore the linear QCA governed by Equation (36) (which does not have eigenvector
. Therefore the linear QCA governed by Equation (36) (which does not have eigenvector![]() ) is thought to be described by the superposition of two (something like “forward going” and “backward going” corresponding to
) is thought to be described by the superposition of two (something like “forward going” and “backward going” corresponding to![]() ) TDSEs in the wavenumber
) TDSEs in the wavenumber
![]() limit just like the advection type linear QCA (see [22] ). Now we assume the form of Equation (40) as in the case of type-0 NLQCA (Equations (28) (29)) expecting to obtain type-2 NLQCA.
limit just like the advection type linear QCA (see [22] ). Now we assume the form of Equation (40) as in the case of type-0 NLQCA (Equations (28) (29)) expecting to obtain type-2 NLQCA.
![]() (40)
(40)
However this time ![]() is expressed as Equation (41), not in a rational form.
is expressed as Equation (41), not in a rational form.
![]() (41)
(41)
It is not straightforward to represent type-2 real-LFMT NLQCA using continuum limit approach as in the case of type-0 NLQCA.
6.2. Relation between Type-2 Large Amplitude and Type-0 Small Amplitude
In this section, we try to understand the large amplitude behavior of type-2 NLQCA by relating it to the small amplitude behavior of type 0. Using both-sides inversion and
conjugation formula ![]() ((54) in Appendix A), we can state that if z evolves by type-0 NLQCA
((54) in Appendix A), we can state that if z evolves by type-0 NLQCA ![]() then
then ![]() evolves by type-2 NLQCA
evolves by type-2 NLQCA![]() . So if
. So if ![]() obeying type-0 NLQCA
obeying type-0 NLQCA ![]() varies slowly in space, and its continuum limit is some PDE for
varies slowly in space, and its continuum limit is some PDE for![]() , then the continuum limit of type-2 NLQCA
, then the continuum limit of type-2 NLQCA ![]() is expected to become approximately the PDE rewritten for
is expected to become approximately the PDE rewritten for![]() .
.
(Note that it is important to consider the pair not of ![]() but of
but of![]() . Using
. Using ![]() means using
means using
![]()
for the adjacent grid points pair which causes sign alternating behavior of![]() .)
.)
We numerically examine the validity of the approximation in the case of inviscid Burges equation. Inviscid Burgers case (type-G) is the most promising for the above
continuum limit argument to be applicable because the PDE for ![]() is unitary time
is unitary time
evolution too. (This can be easily verified by the fact that the flux ![]() in Equation (35) contains only
in Equation (35) contains only![]() .)
.)
In Figure 15, we show the simulated NLQCA waveforms of both ![]() for
for
![]() and
and ![]() for
for![]() . Two waveforms match
. Two waveforms match
well, although a certain adjusting parameter ![]() need to be introduced.
need to be introduced.
Note that we do not plot the solution of the inversed Burgers equation itself but plot its inverted values. Initial waveform for Burgers equation is
![]()
and its inverse is used for the inversed Burgers equation.
7. Conclusion
Linear fractional map type (LFMT) nonlinear QCA (NLQCA), is studied analytically as well as numerically. Firstly we introduce LFMT phase rotation which maps the complex plane to itself conserving its absolute value. We employ this LFMT phase rotation in
![]()
Figure 15. The comparison of the type-0 NLQCA solution of the Burgers equation ![]() (G-type, ID = 50) (solid red) and type-2 NLQCA solution for the inversed Burgers equation
(G-type, ID = 50) (solid red) and type-2 NLQCA solution for the inversed Burgers equation ![]() (dashed green).
(dashed green).
two ways in order to construct reversible NLQCA, namely complex-LFMT NLQCA and real-LFMT NLQCA. In order to categorize the qualitative behavior of the LFMT NLQCA, stability analysis around fix points is introduced. Complex- and Real-LFMT NLQCA are studied numerically using a simple model. Results are summarized and analyzed according to the category by the symmetry classification for real-LFMT NLQCA. We further study the continuum limit of the real-LFMT NLQCA analytically and verify it numerically. Linear advection equation or Time Dependent Schrödinger Equation (TDSE) is obtained from the continuum limit of linear QCA. Similarly it is found that nonlinear advection-diffusion equations including inviscid Burgers equation and porous-medium equation are obtained from real-LFMT NLQCA. Although it is already reported in the article [21] the emergence of this porous-medium equation as the continuum limit of some NLQW, real-LFMT NLQCA in our study includes more general dynamics. We also observe soliton-like behavior.
Acknowledgements
This research was supported by TUT Programs on Advanced Simulation Engineering, Toyohashi University and University-Community Partnership promotion center, Toyohashi University. We would like to thank Prof. Hitoshi Goto for his support.
Appendix A: Formulas on LFMT Phase Rotation
As mentioned in 2.1, ![]() and
and ![]() denotes the function
denotes the function ![]()
Scale transformation
![]() (42)
(42)
Inverse transformation
![]() (43)
(43)
By clearing the fraction of the left equation and replacing zz* with z'z'* the right equation is obtained. Namely
![]() (44)
(44)
is obtained.
Rotation
![]() (45a)
(45a)
![]() (45b)
(45b)
![]() (45c)
(45c)
![]() (45d)
(45d)
Here A, B are constants, or A, B can be functions of |$| if |k| = 1.
[Proof]
Equation (45a) is the special case of the general formula![]() . Equation (45b) is obvious from
. Equation (45b) is obvious from
![]()
(Note that the factor u(k) must be factored out to the left, or $ (=evaluated value of the right side) would be changed.)
Equations (45c) and (45d) can be obtained from Equations (45b) and (45a) respectively by applying C from the right and using Equation (48). Note that if |k| = 1 Equations (45c) and (45d) can be obtained also by replacing A with ![]() in Equations (45a) and (45b).
in Equations (45a) and (45b).
Both sides conjugation
![]() (46)
(46)
A, B can be a function of |$|.
[Proof]
![]() (47)
(47)
Right side conjugation
![]() (48)
(48)
A, B can be a function of |$|. This formula means that type-0 LFMT phase rotation is related to type-2 LFMT phase rotation via complex conjugation (C).
[Proof]
![]() (49)
(49)
[Remark]
A, B can be a function of |$|. Therefore especially for type-1 and type-2
![]() (50a)
(50a)
![]() (50b)
(50b)
are satisfied.
Left side conjugation
![]() (51)
(51)
Note that the left side conjugation is equivalent to the both sides inversion if A and B are swapped (see Equation (52)). A, B can be a function of |$|.
[Proof]
It is obvious by applying the right side conjugation formula then the both side inversion formula.
Both side inversion
![]() (52)
(52)
[Proof]
![]() (53)
(53)
Both side inversion and conjugation
![]() (54)
(54)
It is easily derived from both side inversion and both side conjugation formulas. Different from conjugation formula, A, B cannot be regarded as a general function of |$| in (52)-(54).
Composition of mappings
![]() (55)
(55)
As A, B, A', B' are functions of |$|, it is closed. Especially for type-1
![]() (56)
(56)
Therefore it is closed even when A, B, A', B' are restricted to fixed complex number.
Appendix B: Continuous Time Version on LFMT Phase Rotation
Here we discuss extension of the discrete time LFMT phase rotation to the continuous time LFMT phase rotation. This discussion may be the foundation for the more complicated problem such as the continuum limit of the complex-LFMT NLQCA. It is well known that infinitesimal LFM is governed by Riccati-type equation [24] .
Consider the differential equation for ![]()
![]() (57)
(57)
By integrating for unit time, we obtain LFMT phase rotation.
![]() (58)
(58)
Here A, B can be a function of |z|.
[Proof]
Assume that the continuous time extension of (58) obeys the following differential equation Equation (59) in the polar coordinate![]() .
.
![]() (59)
(59)
Let ![]() then using
then using
![]() (60)
(60)
We have the following Riccati equation.
![]() (61)
(61)
Riccati equation can be linearized by setting ![]()
![]() (62)
(62)
And the time evolution is expressed as follows.
![]() (63)
(63)
By setting
![]() (64)
(64)
and using the relation ![]() (I: unit matrix),
(I: unit matrix),
![]() (65)
(65)
is obtained. Therefore the time evolution of ![]() is expressed in the form of LFM as follows.
is expressed in the form of LFM as follows.
![]() (66)
(66)
By comparing with Equation (5), (written again here as Equation (67))
![]() (67)
(67)
We have
![]() (68)
(68)
Reversely (a, b, c) can be obtained from (A, B) by using
![]() (69)
(69)
as
![]() (70)
(70)
From this and setting![]() , we have the goal equation Equation (57).
, we have the goal equation Equation (57).
[Remark]
The point where ![]() is not singular. True singular point is only
is not singular. True singular point is only
the point where![]() . The condition
. The condition ![]() is the condition that there is no fixed point. (namely phase is always circulating). In the case of
is the condition that there is no fixed point. (namely phase is always circulating). In the case of![]() ,
,
we use ![]() and both
and both ![]() and
and ![]() are pure imaginal then a, b, c are real. Although
are pure imaginal then a, b, c are real. Although ![]() (namely multivalued) when real (B)
(namely multivalued) when real (B)
= 0, the sign does not affect the integrated result.
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jqis@scirp.org