Investigative Report for Economists; “Prediction of Stock Market” and Functional “Invisible Hand” and “Law of Supply and Demand” ()
1. Introduction
This paper is an investigative scientific report for economists about the theoretical problems in economics, such as: 1) the “prediction of stock price”; 2) the “invisible hand”; as well as 3) the law of “supply and demand”. The author is interested in the economic science from an alternative science perspective. In addition, he has some innovative scientific research reports [1] [2] related to the economic science. They are related to the solution for complex systems in nature, such as the stock market, ecosystems, thermodynamic systems, etc. He would like to suggest a useful idea for economists from the research.
In the past, many physicists at NASA went to work at Wall Street, but nobody succeeded there. They found that the stock market exhibited a “random walk”. Why did they fail? The stock market is a representatively complex system in nature. For instance, if someone solved the stock market system by other science, the systems’ analysis theory in engineering, based on the multidisciplinary science shown in Figure 1(a), in the other word, the systematic economic problem could not solve the algebraic conventional physics based on reductionism, but the problem can be solved with other science such as theory [3] . Bear in mind. Does everyone agree with it?
However, why cannot many physicists and other scientists solve the problem? The reason is the basic rule of physics. Note that most physical phenomena must entirely be measurable and reversible; otherwise, it cannot be treated as a physical element. Nevertheless, the stock market is endlessly and extremely varying in time, almost exhibiting a “random walk”. We can measure it that the problem must be solved by other science, such as the time series function in real time [3] . Therefore, if we can trust it, we can solve the problems, “prediction of stock price”, and “invisible hand” from Adam Smith, and “the law of supply and demand” in economics. It would be good news to everyone and will be a sensational scientific result for economists, similar to Galileo’s theory a few centuries ago.
![]()
Figure 1. (a) Basic conceptual solution; (b) Conception of the solution as a basic feedback system.
Nevertheless, there is a problem. It is very difficult for economists to understand this without the knowledge of other science such as the systems’ analysis theory. We advised to them: they must spend their money, time, and effort to studying the other science―it is not free!
2. Method
We built a hypothesis from the inner structure of the stock market in Figure 1(b). We can solve the problem easily as follows. Please listen carefully, there are sellers named G and buyers named H. G wishes to sell stock at a higher price, whereas H wishes to buy stock at a lower price with a time delay t. We can formulate a relationship between G and H and substitute, equivalently, a feedback system with a self-controlling property based on the law of the conservation of energy, (It is a keyword) as shown in Figure 1(b). The stock market constantly keeps on counterbalancing without runaway, overflow, or explosion. This information is very significant to us; it is safe for economists as well. Refer to [1] and [2] . If we are acknowledging it, we can solve it easily.
The primary topic; “we cannot predicting the stock market,” is answer here; the stock market causes a feedback system; therefore, we cannot predict it completely and perfectly. If someone was to fix and measure it by tool, we could easily forecast it. If someone wanted to win in the stock market, they would have to bear in mind its properties.
By the way, we can demonstrate the stock price using a simulator [2] . The experiment is performed in two steps as follows.
Step one: In the case of listing on the stock market, we can obtain the response of the unit step function, as shown in Figure 2(b), by the experiment using the simulator.
The mathematical process [3] is described here. The transfer function 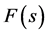 in Figure 1(b) is
in Figure 1(b) is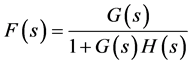 . And the input function
. And the input function  is
is 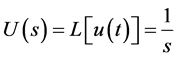 . The basic system algorithm as an equation is
. The basic system algorithm as an equation is
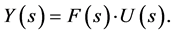 (1)
(1)
We substitute and develop the equation with variables  and
and 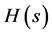 in the general equation
in the general equation  or
or  [3] . The equation the becomes
[3] . The equation the becomes
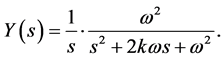 (2)
(2)
Therefore, the process is a normal analyzing process. The transformed reversible Laplace form is
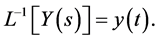 (3)
(3)
We can obtain
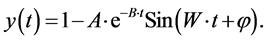 (4)
(4)
where A, B, W, and  are constants, and t is real time [3] .
are constants, and t is real time [3] .
Equation (4) can be characterized in Figure 2(b). We can confirm other information from the complex systems in that it has a sinusoidal period. Therefore, we already know that the stock price is periodic and, eventually, 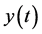 converges to unity. In addition, it displays a strong sensitivity to initial conditions, a phenomenon known as the butterfly effect, which could also be responsible for the periodic phenomenon. The decreasing sine curve has properties similar to self-organization and fractals. Further, it exhibits chaotic properties and the output and input is irreversible [4] .
converges to unity. In addition, it displays a strong sensitivity to initial conditions, a phenomenon known as the butterfly effect, which could also be responsible for the periodic phenomenon. The decreasing sine curve has properties similar to self-organization and fractals. Further, it exhibits chaotic properties and the output and input is irreversible [4] .
Step two: The other case of variable information in the stock market is if a random function 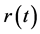 is added to the system simulator. We can observe what happens with the display by viewing Figure 2(c). It displays a response that fluctuates violently with time, and is overlapped with chaos, fractals, self-organization, and the butterfly effect, among others [4] . Therefore, we cannot determine anything substantial. It is the “random walk” commonly talked about among physicists. Finally, no one can predict the stock price absolutely.
is added to the system simulator. We can observe what happens with the display by viewing Figure 2(c). It displays a response that fluctuates violently with time, and is overlapped with chaos, fractals, self-organization, and the butterfly effect, among others [4] . Therefore, we cannot determine anything substantial. It is the “random walk” commonly talked about among physicists. Finally, no one can predict the stock price absolutely.
Moreover, we can discern other properties from the experiment. The stock market could be externally controlled manually by humans and the circuit break in the stock market is a tool similar to the time delay. This solution can be applied to other systems such as social or political systems as well as exchange rates and money trading control, all based on a machine as MATLAB [3] .
3. Result and Discussion
We found the hidden secret in the stock price using the hypothesis in Section 2. Fur-
![]()
Figure 2. (a) Overview of the solution; (b) Response of the unit step function ; (c) response of the random function
; (c) response of the random function![]() : Exhibits chaotic and fractal self-organization behavior as well as characteristics of the butterfly effect.
: Exhibits chaotic and fractal self-organization behavior as well as characteristics of the butterfly effect.
thermore, we could prove other topics by the same method. The secondary topic, the “invisible hand” by Adam Smith has the same algorithm of the stock market: it is self- controlled for counterbalancing similar to automatic regulating systems. The relationship is characterized by Figure 2(a) but cannot be calculated manually; the equation was produced in MATLAB.
The third topic, the law of “supply and demand” is identical to the “invisible hand.” Therefore, we can solve all three topics successfully, as shown in Figure 2(a). Furthermore, we did not forget one fact: macroeconomics is similar to a systematic problem. Therefore, most economists recommend studying the systems analysis method in engineering. Thus, if someone has any doubt and does not accept this result, we can help support them. The design concept of the system simulator refers to [2] .
4. Conclusion
In summary, economic science is very rational; it is possible to analyze economic systems with the systems’ analysis theory. Therefore, we can easily find the hidden secret in economic systems. The author has spread this solution out to other scientists from economics to philosophy. In conclusion, this report is sufficient for economists.