1. Introduction
It is very easy to get lost in the many [1] and conceptually somewhat very different attempts at the unified field theories. Lastly, the progress [2] at unification has been very slow. Therefore, in this paper in order to “geometrize” the electromagnetic field I will follow neither the scalar gravitational theory of electromagnetism and its introduction of an additional (four spatial and one time dimension) space dimension (Nordström [3] , Kaluza [4] ), nor Weyl’s trial for generalising Riemannian geometry and his concept of “gauging” (Weyl [5] ), nor will I use an asymmetric Ricci tensor (Eddington [6] ), nor will I try to add an antisymmetric tensor to the metric (Bach [7] , Einstein [8] ), nor will I use the framework of quantum field theory et cetera as the point of departure to “geometrize” the electromagnetic field. Theoretically, it seems to be possible to approach unification in the framework of quantum field theory. Still, a satisfactory inclusion of gravitation into the scheme of quantum field theory is not in sight. From this point of view, Finsler [9] geometry introduced by Randers [10] , as a kind of a generalization of Riemann geometry, is another and alternative approach to the geometrization of electromagnetism and gravitation. Taken all together, the point of departure for including the electromagnetic field into a geometric setting will be general relativity. In this context, at least one point has to be considered.
Taken Einstein for granted, we must give up general relativity theory. Einstein himself in his hunt for progress at the unification went so far to force us to give up his own general theory of relativity and the successful geometrization of the gravitational field. According to Einstein, a generalization of the theory of the gravitational field is necessary with the consequence that we must go beyond the general theory of relativity. In this context, Einstein’s position (see Figure 1) concerning the unified field theory is very clear and strict.
Anyhow, if we follow Einstein’s proposal at this point to account for a classical unified field theory of the gravitational and electromagnetic fields with the conceptual unification of the gravitational and electromagnetic field into one single and unique hyper-field [12] , it appears to be necessary and justified on a foundational level to concentrate at the heart of general relativity, the crucial mathematical concept of the metric tensor field gµv.
The following paper can be characterized as follows. The attempt to develop some new, basic and fundamental insights is grounded on a deductive-hypothetical methodological approach. In the section material and methods the basic mathematical objects and tensor calculus rules needed to achieve the “geometrization” of the electromagnetic field will be defined and described.
In this context, physicists should be able to follow the technical aspects of this paper without any problems, while reader without prior knowledge of general relativity or of the mathematics of tensor calculus might gain an insight into the new methods and the scientific background involved. In general, it is necessary to decrease the amount of notation needed. Thus far, I will restrict myself as much as possible to covariant second rank tensors. I apologize for the shortcoming.
Especially, to enable the fusion of quantum theory and relativity theory into a new and single conceptual formalism the starting point of all theorems in the section results is axiom I or +1 = +1 (lex identitatis). The same axiom I possess the strategic capacity to
![]()
Figure 1. Einstein and the problem of the unified field theory.
serve as a common ground for relativity and quantum theory with regard to unified field theory. The section discussion examines some the consequences of the theorems proved. This paper does not provide any proof, whether Einstein’s general theory of relativity is correct or not, this publication assumes only that Einstein’s general theory of relativity is correct.
In this context, from the conceptual point of view of the unified field theory, it is the purpose of this publication to in find a convincing formulation of a geometrization of the electromagnetic fields under conditions of the validity of the general theory of relativity.
2. Material and Methods
2.1. Definitions
Einstein’s General Theory of Relativity
Definition: Einstein’s field equations
Einstein field equations (EFE), originally [13] published [14] without the extra “cosmological” term L ´ gµv may be written in the form
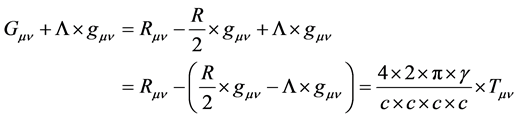 (1)
(1)
where Gµv is the Einsteinian tensor, Tµv is the stress-energy tensor of matter (still a field devoid of any geometrical significance), Rµv denotes the Ricci tensor (the curvature of space), R denotes the Ricci scalar (the trace of the Ricci tensor), L denotes the cosmological “constant” and gµv denotes the metric tensor (a 4 × 4 matrix) and where p is Archimedes’ constant (p = 3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 9∙∙∙), g is Newton’s gravitational “constant” and the speed of light in vacuum is c = 299 792 458 [m/s] in S. I. units.
Scholium.
The stress-energy tensor Tµv, still a tensor devoid of any geometrical significance, contains all forms of energy and momentum which includes all matter present but of course any electromagnetic radiation too. Originally, Einstein’s universe was spatially closed and finite. In 1917, Albert Einstein modified his own field equations and inserted the cosmological constant L (denoted by the Greek capital letter lambda) into his theory of general relativity in order to force his field equations to predict a stationary universe.
“Ich komme nämlich zu der Meinung, daß die von mir bisher vertretenen Feldglei- chungen der Gravitation noch einer kleinen Modifikation bedürfen…” [15] .
By the time, it became clear that the universe was expanding instead of being static and Einstein abandoned the cosmological constant L. “Historically the term containing the “cosmological constant” λ was introduced into the field equations in order to enable us to account theoretically for the existence of a finite mean density in a static universe. It now appears that in the dynamical case this end can be reached without the introduction of λ” [16] . But lately, Einstein’s cosmological constant is revived by scientists to explain a mysterious force counteracting gravity called dark energy. In this context it is important to note that neither Newton’s gravitational “constant” big G [17] [18] nor Einstein’s cosmological constant L [19] is a constant.
Definition: General tensors
Independently of the tensors of the theory of general relativity, we introduce by definition the following covariant second rank tensors of preliminary unknown structure whose properties we leave undetermined as well. We define the following covariant second rank tensors of yet unknown structure as
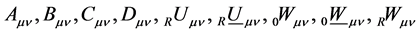 (2)
(2)
while the tensors Aµv, Bµv, Cµv, Dµv may equally denote something like the four basic fields of nature. Especially, the Ricci tensor Rµv itself can be decomposed in many different ways. In the following of this publication we define the following relationships. We decompose the Ricci tensor Rµv by definition as
 (3)
(3)
to assure that both gravitation and electromagnetism is geometrized simultaneously. Since everything is expressed in terms of curvature tensor, the electromagnetic field itself is completely geometrized from the beginning. By the following definition, the electromagnetic stress energy tensor, denoted as Bµv, appears as part of Einstein’s stress- energy tensor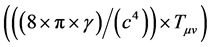 , while the tensor Aµv, also part of curvature, denotes the stress energy tensor of “ordinary” matter. Thus far, we obtain
, while the tensor Aµv, also part of curvature, denotes the stress energy tensor of “ordinary” matter. Thus far, we obtain
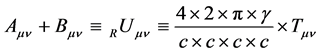 (4)
(4)
Scholium.
By this definition, we are following Vranceanu in his claim that the energy tensor Tkl can be treated as the sum of two tensors one of which is due to the electromagnetic field.
“On peut aussi supposer que le tenseur d’énergie Tkl soit la somme de deux tenseurs dont un dû au champ électromagnétique…” [20] .
In English:
“One can also assume that the energy tensor Tkl be the sum of two tensors one of which is due to the electromagnetic field”.
In other words, the stress-energy tensor of the electromagnetic field Bµv is equivalent to the portion of the stress-energy tensor of energy 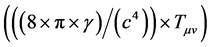 which is determined by the stress energy tensor of the electromagnetic field Bµv itself. The stress-energy tensor Tµv has the unit of energy density [J/m3] or pressure [N/m2] which are actually the same unit. In the International System of Units the joule is a derived unit of energy and is defined as 1[J] = 1[kg×m2/s2] = [N×m] while 1[N] = 1[kg×m/s2] = 1[J/m] denotes the unit of force. Figure 2 may illustrate the relationship above in some more detail.
which is determined by the stress energy tensor of the electromagnetic field Bµv itself. The stress-energy tensor Tµv has the unit of energy density [J/m3] or pressure [N/m2] which are actually the same unit. In the International System of Units the joule is a derived unit of energy and is defined as 1[J] = 1[kg×m2/s2] = [N×m] while 1[N] = 1[kg×m/s2] = 1[J/m] denotes the unit of force. Figure 2 may illustrate the relationship above in some more detail.
Einstein himself was demanding something similar.
“Wir unterscheiden im folgenden zwischen “Gravitationsfeld” und “Materie” in dem Sinne, daß alles außer dem Gravitationsfeld als “Materie” bezeichnet wird, also nicht nur die “Materie” im üblichen Sinne, sondern auch das elektromagnetische Feld.” [14]
We define an anti tensor [2] of Einstein’s stress energy tensor Tµv, as
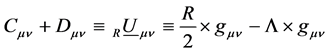 (5)
(5)
while Einstein’s tensor Gµv is defined by
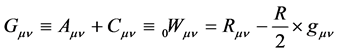 (6)
(6)
where Aµv is the known the stress energy tensor of “ordinary” matter.
Scholium.
One consequence of the definition before is that the tensor of ordinary matter Aµv becomes a joint tensor since the same tensor is a determining part of the Einstein’s stress energy tensor  and equally a determining part of Einsteinian tensor Gµv. In probability theory, such a tensor would represent a joint distribution function. The Ricci scalar curvature R[1/m2] is a contraction of the Ricci tensor Rµv[1/m2]. The Ricci tensor itself is a contraction of the Riemann tensor while a contraction as such doesn’t change the units.
and equally a determining part of Einsteinian tensor Gµv. In probability theory, such a tensor would represent a joint distribution function. The Ricci scalar curvature R[1/m2] is a contraction of the Ricci tensor Rµv[1/m2]. The Ricci tensor itself is a contraction of the Riemann tensor while a contraction as such doesn’t change the units.
Finally, we define an anti-tensor Gµv of Einsteinian tensor Gµv, as
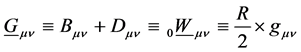 (7)
(7)
Scholium.
The following 2 × 2 table (Table 1) may illustrate the basic relationships above
![]()
Figure 2. The relationship between ordinary matter Aµv and the electromagnetic field Bµv.
![]()
Table 1. The decomposition of the Ricci tensor Rµv in general.
Definition: The stress energy tensor of the electro-magnetic field Bµv
We define the second rank covariant stress-energy tensor of the electromagnetic field Bµv, an anti tensor [2] of the tensor Aµv, as
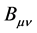 (8)
(8)
Under conditions of general relativity, where Aµv denotes the stress energy tensor of ordinary energy/matter, the stress-energy tensor of the electromagnetic field Bµv is an anti tensor [2] of ordinary energy/matter Aµv. Under conditions of general relativity, the second rank covariant stress-energy tensor of the electromagnetic field Bµv is determined by an anti-symmetric second-order tensor known as the electromagnetic field (Faraday) tensor F. In general, under conditions of general relativity, the second rank covariant stress-energy tensor of the electromagnetic field Bµv in the absence of “ordinary” matter, which itself is different from the electromagnetic field tensor F, can be derived many different ways. One form of this tensor is
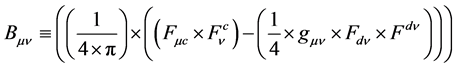 (9)
(9)
where F is the electromagnetic field tensor and gµv is the metric tensor of general relativity.
Scholium.
The probability tensor [2] of the second rank covariant stress-energy tensor of the electromagnetic field Bµv is defined as
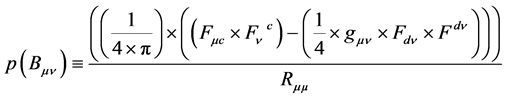 (10)
(10)
One possible theoretical geometric formulation of the stress-energy tensor of the electromagnetic field [2] follows as
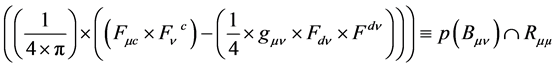 (11)
(11)
Definition of Tensors with relation to the Ricci scalar R
In general, we define the second rank covariant metric tensor Xgµv of the tensor Xµv under conditions of a Ricci scalar as
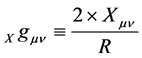 (12)
(12)
where R denotes the Ricci scalar and Xµv denotes a second rank (even a metric) tensor. Thus far, even a metric tensor can possess a metric. A straightforward consequence of this definition is the relationship between the metric tensor Xgµv and the probability tensor p(Xµv) as p(Xµv) Ç Ricgµv = Xgµv. Further, we define n(Xµv) as
![]() (13)
(13)
where R denotes the Ricci scalar and Xµv denotes a second rank (even a metric) tensor. Further, we define ![]() as
as
![]() (14)
(14)
where R denotes the Ricci scalar and Xµv denotes acovariant second rank (even a metric) tensor.
Definition: The tensor n(Aµv)
We define the second rank tensor n(Aµv) as
![]() (15)
(15)
where R denotes the Ricci scalar.
Definition: The metric tensor Agµv
We define the second rank metric tensor Agµv as
![]() (16)
(16)
where R denotes the Ricci scalar.
Definition: The tensor n(Bµv)
We define the second rank tensor n(Bµv) as
![]() (17)
(17)
where R denotes the Ricci scalar.
Definition: The metric tensor Bgµv
We define the second rank metric tensor Bgµv as
![]() (18)
(18)
where R denotes the Ricci scalar.
Definition: The Tensor n ![]()
We define the second rank tensor ![]() as
as
![]() (19)
(19)
where R denotes the Ricci scalar. Due to our definition before it is n(Aµv) = Aµv/R and n(Bµv) = Bµv/R while at the same time it holds true that![]() , the stress energy tensor is decomposed into the tensors Aµv and Bµv.
, the stress energy tensor is decomposed into the tensors Aµv and Bµv.
Definition: The metric tensor Egµv
We define the second rank metric tensor Egµv as
![]() (20)
(20)
where R denotes the Ricci scalar.
Definition: The tensor n(Cµv)
We define the second rank tensor n(Cµv) as
![]() (21)
(21)
where R denotes the Ricci scalar.
Definition: The metric tensor Cgµv
We define the second rank metric tensor Cgµv as
![]() (22)
(22)
where R denotes the Ricci scalar.
Definition: The tensor n(Dµv)
We define the second rank tensor n(Dµv) as
![]() (23)
(23)
where R denotes the Ricci scalar.
Definition: The metric tensor Dgµv
We define the second rank metric tensor Dgµv as
![]() (24)
(24)
where R denotes the Ricci scalar.
Definition: The tensor ![]()
We define the second rank tensor ![]() as
as
![]() (25)
(25)
where R denotes the Ricci scalar.
Definition: The tensor ØEgµv
We define the second rank metric tensor ØEgµv as
![]() (26)
(26)
where R denotes the Ricci scalar.
Definition: The tensor n(Gµv)
We define the second rank tensor n(Gµv) as
![]() (27)
(27)
where R denotes the Ricci scalar and Gµv is the Einsteinian tensor.
Definition: The metric tensor Ggµv
We define the second rank metric tensor Ggµv as
![]() (28)
(28)
where R denotes the Ricci scalar and Gµv is the Einsteinian tensor.
Definition: The tensor n(Gµv)
We define the second rank tensor n(Gµv) as
![]() (29)
(29)
where R denotes the Ricci scalar and Gµv is the anti Einsteinian tensor.
Definition: The metric tensor ØGgµv
We define the second rank metric tensor ØGgµv as
![]() (30)
(30)
where R denotes the Ricci scalar and Gµv is the anti Einsteinian tensor.
Definition: The metric tensor grgµv of the metric tensor gµv
We define the second rank metric tensor grgµv as
![]() (31)
(31)
where R denotes the Ricci scalar where gµv denotes the metric tensor of general relativity theory.
Definition: The tensor n(Rµv)
We define the second rank tensor n(Rµv) as
![]() (32)
(32)
where R denotes the Ricci scalar and Rµv denotes the Ricci tensor.
Definition: The metric tensor Ricgµv
We define the second rank metric tensor Ricgµv as
![]() (33)
(33)
where R denotes the Ricci scalar and Rµv denotes the Ricci tensor.
Scholium.
The following 2 × 2 table (Table 2) may illustrate the basic relationships above
The 2 × 2 table (Table 3) illustrates the basic relationships between the metric tensors.
Definition: The tensor gµv
The mathematics of general relativity are more or less complex. As a result, the curvature of space (represented by the Einstein tensor Gµv) is caused by the presence of matter and energy (represented by the stress-energy tensor Tµv) and vice versa. The cur- vature of space is the cause or determines how matter/energy has to move. The Riemannian metric tensor for a curved space-time of general relativity theory, a kind of generalization of the gravitational potential of Newtonian gravitation, is denoted as
![]() (34)
(34)
In the following, let us define the following. Let
![]()
Table 2. The decomposition of the Ricci tensor Rµv.
![]()
Table 3. The decomposition of the Ricci tensor Rµv in terms of metric tensors.
![]() (35)
(35)
and
![]() (36)
(36)
The (unitless) metric tensor gµv is a central object in general relativity and describes more or less the local geometry of space-time while representing the gravitational potential. The metric tensor determines the invariant square of an infinitesimal line element, denoted as ds and often referred to as an interval. In general, the generalization of the standard measure of distance ds between two points in Euclidian space due to the Pythagorean theorem is defined as
![]() (37)
(37)
or
![]() (38)
(38)
In general, a coordinate system can be changed from the Euclidean Y’s to some coordinate system of X’s then
![]() (39)
(39)
and
![]() (40)
(40)
The Pythagorean theorem is known to be defined as
![]() (41)
(41)
where δmn denotes the known Kronecker delta. Using Einstein’s summation convention, the metric tensor gµv is
![]() (42)
(42)
and a curved space compatible formulation of the Pythagorean theorem follows as usual as
![]() (43)
(43)
In other words, it is
![]() (44)
(44)
Under conditions, where
![]() (45)
(45)
it is
![]() (46)
(46)
Dividing the equation before by the speed of the light squared, c2, it is
![]() (47)
(47)
where tgµv = (1/c2) ´ gµv. The term ds2/c2 yields the time squared or ds2/c2 = dRt2 as do the other terms. The equation before can be rearranged as
![]() (48)
(48)
Rearranging equation, we obtain
![]() (49)
(49)
or while using Einstein’s summation convention,
![]() (50)
(50)
or
![]() (51)
(51)
Multiplying by ((R/2) − Λ), it is
![]() (52)
(52)
Definition: The metric tensor of the electromagnetic field EMgµv
We define the second rank metric tensor of the electro-magnetic field EMgµv of preliminary unknown structure as
![]() (53)
(53)
where Y denotes an unknown (i.e. scalar) parameter. Due to this definition, it is Bµv = Y ´ EMgµv.
Definition: The anti metrictensor of the electromagnetic field 0gµv or Wgµv
We define the second rank anti metric tensor of the electro-magnetic field Wgµv of preliminary unknown structure as
![]() (54)
(54)
where Y denotes an unknown (i.e. scalar) parameter. Due to this definition, it is Dµv = Y ´ Wgµv.
Definition: The relationships between the metric tensors
In general, the metric tensor for a curved space-time of general relativity theory is equally determined as
![]() (55)
(55)
where EMgµv = gµv ? Wgµv and EMgµv denotes the second rank metric tensor of the electro- magnetic field while Wgµv is the second rank anti metric tensor of the electro-magnetic field. Both tensors are of still unknown structure. From this definition, it follows that
![]() (56)
(56)
Scholium.
The true meaning of the metric tensor Wgµv is not clear at this moment. One is for sure, the same tensor is an anti-tensor of the metric tensor of the electromagnetic field EMgµv. There is some theoretical possibility that the tensor Wgµv is related to something like the metric tensor of the gravitational waves, therefore the abbreviation Wgµv.
Definition: The tensor of energy of the unified field theory REµv
In order to assure compatibility between general theory of relativity and the unified field theory, we define the following relationship between the stress energy tensor ![]() of general relativity and the tensor of energy [2] of unified field theory REµv as
of general relativity and the tensor of energy [2] of unified field theory REµv as
![]() (57)
(57)
while the value of X is undermined at this moment. The value of X can be X = 1.
Definition: The tensor of time of the unified field theory Rtµv
In order to assure compatibility between the second rank tensor ![]() of general theory of relativity and tensor of time [2] Rtµv of the unified field theory, we define the following relationship.
of general theory of relativity and tensor of time [2] Rtµv of the unified field theory, we define the following relationship.
![]() (58)
(58)
while the value of X is undermined at this moment. The value of X can be X = 1.
Definition: The tensor of space of the unified field theory RSµv
In order to assure compatibility between the second rank Ricci tensor Rµv of general theory of relativity and tensor of space [2] RSµv of the unified field theory, we define the following relationship.
![]() (59)
(59)
while the value of X is undermined at this moment. The definition before does not exclude the case that X = 1.
2.2. Axioms
2.2.1. Axiom I. (Lex Identitatis. Principium Identitatis. The Identity Law)
The foundation of all what may follow is the following axiom:
![]() (60)
(60)
2.2.2. Axiom II
![]() (61)
(61)
2.2.3. Axiom III
![]() (62)
(62)
Remark.
In order to avoid any kind of an inconsistency and to obtain a theory that also prove to be universally valid, the axioms and rules of this publication are chosen very carefully. Especially to face singularity problems of general relativity, the axioms II and III can be of use. However, today it is far from clear whether axiom II and axiom III can be treated as generally valid. Usually the chance of proving the consistency of axioms is sometimes temporary limited. By time objective reality or scientific experiments or human practice as such is the main proof of any axiomatic theory. More precisely, special experimental settings satisfying some certain conditions can disproof any formal deductive systems or axiomatic theory. There is already some evidence, that axiom III [21] is correct.
3. Results
3.1. Theorem. The Unification of Gravity and Electromagnetism
Claim. (Theorem. Proposition. Statement.)
In general, the gravitational and the electromagnetic field can be joined into one single hyperfield which itself is completely determined by the geometrical structure of the space-time. We obtain
![]() (63)
(63)
Direct proof.
In general, using axiom I is it
![]() (64)
(64)
Multiplying this equation by the stress-energy tensor of general relativity![]() , it is
, it is
![]() (65)
(65)
where γ is Newton’s gravitational “constant” [17] [18] , c is the speed of light in vacuum and![]() , sometimes referred to as “Archimedes” constant’, is the ratio of a circle’s circumference to its diameter. Due to Einstein’s general relativity, the equation before is equivalent with
, sometimes referred to as “Archimedes” constant’, is the ratio of a circle’s circumference to its diameter. Due to Einstein’s general relativity, the equation before is equivalent with
![]() (66)
(66)
where Rµv is the Ricci curvature tensor (the trace of Rimanian curvature tensor), R is the scalar curvature, gµv is the metric tensor, Λ is the cosmological constant and Tµv is the stress-energy tensor. By defining the Einstein tensor as![]() , it is possible to write the Einstein field equations in a more compact as
, it is possible to write the Einstein field equations in a more compact as
![]() (67)
(67)
Due to our definition above it is Gµv = Aµv + Cµv. Substituting this relationship into the equation before, we obtain
![]() (68)
(68)
Under these conditions, we recall our definition before where ![]()
![]() . Substituting this relationship into the equation before, we obtain
. Substituting this relationship into the equation before, we obtain
![]() (69)
(69)
where Aµv denotes the stress energy tensor of ordinary matter and Bµv denotes the stress energy tensor of the electromagnetic field. Simplifying equation, it is
![]() (70)
(70)
where Cµv denotes the gravitational field due to the stress energy tensor of ordinary matter Aµv. We add the tensor Cµv on both sides of the equation before. The unification of gravity and electromagnetisms under conditions of general relativity theory follows as
![]() (71)
(71)
or in general as
![]() (72)
(72)
Quod erat demonstrandum.
Scholium.
The theorem of the unification of gravity and electromagnetism does not contain any additional fields and is formulated in four-dimensional space-time. Thus far, within the sum of the tensors Bµv + Cµv, both electromagnetism and gravity are successfully unified and linked to each other. Up to now, there is neither theoretical nor experimental evidence that there might be unobserved additional fields or extra dimensions necessary for the unification of gravity and electromagnetism. Therefore, for geometry underlying the theorem of the unification of gravity and electromagnetism we choose Riemannian geometry which is known to be suitable for gravitational interaction. Accordingly, until today all attempts known to geometrize electromagnetism or unify electromagnetism with gravitation in the framework of Riemannian geometry were in vain. Still, the theorem of the unification of gravity and electromagnetism demonstrates equally that Riemannian geometry is appropriate for unification of gravitation and electromagnetism. The most important and interesting thing is a prediction of the theorem of the unification of gravity and electromagnetism that the stress energy tensor of the electromagnetic field Bµv is a source for ordinary gravitational field Cµv. From physical point of view, this prediction can be confirmed by experiments in strong electromagnetic field very precisely.
Lastly, the electromagnetic field Bµv is a source for the ordinary gravitational field Cµv since both fields are related by the equation ![]() and the ordinary gravitational field Cµv is itself is a determining part of Einstein’s tensor Gµv. Furthermore, the ordinary gravitational field Cµv when the stress energy tensor of the electromagnetic field Bµv is equal to zero (Bµv = 0) is still determined by the equation
and the ordinary gravitational field Cµv is itself is a determining part of Einstein’s tensor Gµv. Furthermore, the ordinary gravitational field Cµv when the stress energy tensor of the electromagnetic field Bµv is equal to zero (Bµv = 0) is still determined by the equation![]() . Thus far, under these circumstances it is
. Thus far, under these circumstances it is ![]() and the ordinary gravitational field Cµv is given exactly by the equation Cµv = −Λ ´ gµv.
and the ordinary gravitational field Cµv is given exactly by the equation Cµv = −Λ ´ gµv.
In conclusion, we note that when the ordinary gravitational field Cµv is equal to zero or Cµv = 0 the stress energy tensor of the electromagnetic field Bµv derived from the equation ![]() is determined in this context by the equation
is determined in this context by the equation ![]()
![]() . In other words, we obtain Λ ´ gµv = Bµv. Under these conditions, the metric tensor EMgµv of the stress-energy tensor of the electromagnetic field Bµv follows in general from the equation
. In other words, we obtain Λ ´ gµv = Bµv. Under these conditions, the metric tensor EMgµv of the stress-energy tensor of the electromagnetic field Bµv follows in general from the equation ![]() as
as ![]()
![]() .
.
3.2. Theorem. The Anti Einsteinian Tensor Gµv
Claim. (Theorem. Proposition. Statement.)
The anti Einsteinian tensor Gµv is determined as
![]() (73)
(73)
Direct proof.
In general, using axiom I is it
![]() (74)
(74)
Multiplying this equation by the Ricci Tensor Rµv, it is
![]() (75)
(75)
Due to our definition above, it is![]() . Substituting this relationship into the equation before, we obtain
. Substituting this relationship into the equation before, we obtain
![]() (76)
(76)
The sum of the tensor Gµv = Bµv + Dµv can be obtained as
![]() (77)
(77)
which can be simplified as
![]() (78)
(78)
Due to our definition, Einsteinian tensor Gµv is defined as Gµv = Aµv + Cµv. Rearranging equation above, it is
![]() (79)
(79)
Einstein’s tensor Gµv is defined as![]() . Substituting this relationship into the equation before, we obtain
. Substituting this relationship into the equation before, we obtain
![]() (80)
(80)
Rearranging equation, we obtain
![]() (81)
(81)
At the end, we obtain
![]() (82)
(82)
Quod erat demonstrandum.
3.3. Theorem. The Determination of the Unknown Parameter Y
Claim. (Theorem. Proposition. Statement.)
The unknown parameter Y is determined as
![]() (83)
(83)
where R denotes the Ricci scalar.
Direct proof.
In general, using axiom I is it
![]() (84)
(84)
Multiplying this equation by the anti Einsteinian tensor Gµv, it is
![]() (85)
(85)
The same tensor was determined by the theorem before as Bµv + Dµv = Gµv. Substituting this relationship into the equation before, we obtain
![]() (86)
(86)
Due to our definition above, it is as Bµv = Y ´ EMgµv and Dµv = Y ´ Wgµv. Substituting this relationship into the equation before, we obtain
![]() (87)
(87)
Due to our definition gµv = EMgµv + Wgµv, the equation before can be rearranged as
![]() (88)
(88)
In other words, it is
![]() (89)
(89)
A further manipulation of the equation before yields the result that
![]() (90)
(90)
Quod erat demonstrandum.
Scholium.
Such a result is logical too. Due to our definition it is
![]() (91)
(91)
where EMgµv = gµv − Wgµv and EMgµv denotes the second rank metric tensor of the electro- magnetic field while Wgµv is the second rank anti metric tensor of the electro-magnetic field. Multiplying equation above by the term (R/2), we obtain
![]() (92)
(92)
which is exactly the result as obtained above.
3.4. Theorem. The Geometrization of the Stress-Energy Tensor of the Electromagnetic Field
Claim. (Theorem. Proposition. Statement.)
The geometrization of the stress-energy tensor of the electromagnetic field under conditions of general relativity follows as
![]() (93)
(93)
where R denotes the Ricci scalar and EMgµv denotes the metric tensor of the electromagnetic field.
Direct proof.
In general, using axiom I is it
![]() (94)
(94)
Multiplying this equation by the stress-energy tensor of the electromagnetic field, denoted as Bµv, it is
![]() (95)
(95)
Due to our definition above, the stress-energy tensor of the electromagnetic field was determined by the relationship Bµv = Y ´ EMgµv. Rearranging the equation before we obtain
![]() (96)
(96)
According to the theorem before, the unknown parameter Y is determined as Y = R/2. The geometrization of the electromagnetic field under conditions of general relativity follows as
![]() (97)
(97)
Quod erat demonstrandum.
Scholium.
In a more far reaching development, at least since general relativity theory brought the geometry to the scenario of physics, many attempts were made to extend general relativity’s geometrization of gravitation to non-gravitational fields. In particular, the geometrization of the electromagnetic field became a principal focus and a cornerstone of physical interest and inquiry. The many geometric theories of electromagnetism as published meanwhile are still not consistent with the framework of the quantum theory or self-contradictory, despite the fact that the electromagnetic theory was consolidated in the 19th century. The present theorem before describes the stress-energy tensor of the electro-magnetic field as directly related or determined by the space-time geometry or the metric tensor EMgµv. A unified field theory, in the sense of a completely geometrical field theory of all fundamental interactions, is no longer only a theoretical desire.
3.5. Theorem. The Determination of the Metric Tensor of the Electromagnetic Field EMgµv
Claim. (Theorem. Proposition. Statement.)
The metric tensor of the electromagnetic field EMgµv under conditions of general relativity is determined as
![]() (98)
(98)
where R denotes the Ricci scalar and EMgµv denotes the metric tensor of the electromagnetic field.
Direct proof.
In general, using axiom I is it
![]() (99)
(99)
Multiplying this equation by the stress-energy tensor of the electromagnetic field, abbreviated as Bµv, it is
![]() (100)
(100)
Due to our theorem before, the geometrization of the electromagnetic field under conditions of general relativity is determined as
![]() (101)
(101)
The stress-energy tensor of the electromagnetic field Bµv is determined in detail i.e. by the relationship
![]() (102)
(102)
where F is the electromagnetic field tensor and gµv is the metric tensor. The equation before changes to
![]() (103)
(103)
The metric tensor of the electromagnetic field EMgµv under conditions of general relativity is determined as
![]() (104)
(104)
Quod erat demonstrandum.
3.6. Theorem. The Tensor Cµv
Claim. (Theorem. Proposition. Statement.)
The tensor Cµv is determined as
![]() (105)
(105)
Direct proof.
In general, using axiom I is it
![]() (106)
(106)
Multiplying this equation by the stress-energy tensor of the electromagnetic field, denoted as Bµv, it is
![]() (107)
(107)
Due to our theorem before, the metric tensor of the electromagnetic field under conditions of general relativity is determined as
![]() (108)
(108)
where R denotes the Ricci scalar and EMgµv denotes the metric tensor of the electromagnetic field. Due to the another theorem above, it is
![]() (109)
(109)
The tensor Cµv is determined by the stress energy tensor of the electromagnetic field Bµv as
![]() (110)
(110)
Quod erat demonstrandum.
Scholium.
Lastly, the stress-energy tensor of the electromagnetic field Bµv is a source or a determining part for the ordinary gravitational field Cµv. From physical point of view, this theorem can be confirmed by experiments in strong electromagnetic fields.
3.7. Theorem. The Determination of Tensor of the Hyperfield of Gravitation and Electromagnetism
Claim. (Theorem. Proposition. Statement.)
The geometrized form of the hyper-tensor of unification of gravitation and electromagnetism is determined as
![]()
Direct proof.
In general, using axiom I is it
![]() (111)
(111)
Multiplying this equation by the stress-energy tensor of the electromagnetic field, denoted as Bµv, it is
![]() (112)
(112)
Due to our theorem before, the stress energy tensor of the electromagnetic field under conditions of general relativity is determined as
![]() (113)
(113)
where R denotes the Ricci scalar and EMgµv denotes the metric tensor of the electromagnetic field. Due to a theorem before, it is
![]() (114)
(114)
The tensor Cµv is determined by the stress energy tensor of the electromagnetic field Bµv as
![]() (115)
(115)
Adding the stress-energy tensor of the electromagnetic field Bµv = (R/2) ´ EMgµv to the equation before, we obtain the geometrized form of the hyper-tensor of Cµv puls Bµv (i.e. the unity of gravitation and electromagnetism) as
![]() (116)
(116)
Quod erat demonstrandum.
3.8. Theorem. The Tensor Dµv
Claim. (Theorem. Proposition. Statement.)
The tensor Dµv is determined as
![]() (117)
(117)
Direct proof.
In general, using axiom I is it
![]() (118)
(118)
Multiplying this equation by the stress-energy tensor of the electromagnetic field, denoted as Bµv, it is
![]() (119)
(119)
Due to our theorem before, the stress energy tensor of the electromagnetic field under conditions of general relativity is determined as
![]() (120)
(120)
where R denotes the Ricci scalar and EMgµv denotes the metric tensor of the electromagnetic field. Adding the tensor Dµv, we obtain
![]() (121)
(121)
According to a theorem before, this relationship is equivalent with
![]() (122)
(122)
Rearranging the equation before, the tensor Dµv is determined as
![]() (123)
(123)
Quod erat demonstrandum.
3.9. Theorem. The Geometrization of the Stress Energy Tensor of “Ordinary” Matter Aµv
Claim. (Theorem. Proposition. Statement.)
The geometrization of the stress-energy tensor of “ordinary” matter Aµv can be obtained as
![]() (124)
(124)
Direct proof.
In general, using axiom I is it
![]() (125)
(125)
Multiplying this equation by the Ricci Tensor Rµv, it is
![]() (126)
(126)
Due to our definition above, it is![]() . Substituting this relationship into the equation before, we obtain
. Substituting this relationship into the equation before, we obtain
![]() (127)
(127)
The tensor of ordinary matter Aµv follows as
![]() (128)
(128)
The tensor Bµv itself was determined as![]() . The addition of the tensors Dµv plus Cµv is determined as
. The addition of the tensors Dµv plus Cµv is determined as![]() . The equation before changes to
. The equation before changes to
![]() (129)
(129)
Rearranging equation before, we obtain
![]() (130)
(130)
The tensor (R/2) ´ gµv is determined as![]() . The equation can be simplified as
. The equation can be simplified as
![]() (131)
(131)
The geometrization of “ordinary” matter follows in general as
![]() (132)
(132)
Quod erat demonstrandum.
3.10. Theorem. The Probability Tensor of the Electromagnetic Field p(Bµv)
Claim. (Theorem. Proposition. Statement.)
The probability tensor p(Bµv) of the stress-energy tensor of the electromagnetic field is determined as
![]() (133)
(133)
Direct proof.
In general, using axiom I is it
![]() (134)
(134)
Multiplying this equation by the stress-energy tensor of the electromagnetic field, denoted as Bµv, it is
![]() (135)
(135)
Due to our theorem before, the geometrization of the electromagnetic field under conditions of general relativity is determined as
![]() (136)
(136)
The stress-energy tensor of the electromagnetic field Bµv was determined i.e. by the relationship
![]() (137)
(137)
where F is the electromagnetic field tensor and gµv is the metric tensor. The equation before changes to
![]() (138)
(138)
The Ricci scalar R is defined as the contraction of the Ricci tensor Rµv or it is R = gµvRµv. The equation before changes to
![]() (139)
(139)
A commutative division [2] by the Ricci tensor Rµv leads to the relationship
![]() (140)
(140)
This equation is identical with the probability tensor p(Bµv) of the stress-energy tensor of the electromagnetic field. In general it is
![]() (141)
(141)
Quod erat demonstrandum.
3.11. Theorem. The Probability Tensor Is Determined by the Metric Tensor
Claim. (Theorem. Proposition. Statement.)
In general let n(Xµv) = Xµv/R where Xµv denotes a second rank co-variant tensor and R denotes the Ricci scalar, the contraction of the Ricci tensor as R = gµvRµv. Further, p(Xµv) = Xµv/Rµv denotes the probability tensor [2] of the tensor Xµv. The probability tensor p(Xµv) of a tensor Xµv is determined by the metric tensor as
![]() (142)
(142)
Direct proof.
In general, using axiom I is it
![]() (143)
(143)
Multiplying this equation by the tensor Xµv, it is
![]() (144)
(144)
A commutative [2] division of the tensor Xµv by the Riccitensor Rµv yields
![]() (145)
(145)
which is equivalent with
![]() (146)
(146)
or with
![]() (147)
(147)
Rearranging equation it is
![]() (148)
(148)
Changing equation, we obtain
![]() (149)
(149)
Due to the relationship R = gµvRµv, the equation before simplify as
![]() (150)
(150)
or as
![]() (151)
(151)
In general, it is n(Xµv) = Xµv/R. The probability tensor of a tensor Xµv is determined by the (inverse or) conjugate metric tensor as
![]() (152)
(152)
Quod erat demonstrandum.
Scholium.
Quantum physics (quantization) focuses on the probability (amplitudes) while general relativity theory relies on geometry (tempo-spatial points). The definition of a probability tensor p(Xµv) of a tensor Xµv marks a remarkable degree of interaction between probability theory and the highly dimensional theory of general relativity and is a key step to the unification of quantum physics and general relativity by probabilitizing general relativity’s geometric background. In principle, a contradiction free transformation of a geometrical mathematical framework into a probabilistic mathematical framework and vice versa is possible. A geometrization of probability theory appears to be necessary too.
3.12. Theorem. The Normalization of the Relationship between the Tensors of General Theory of Relativity
Claim. (Theorem. Proposition. Statement.)
The relationship between the tensors of general theory of relativity can be normalized as
![]() (153)
(153)
Direct proof.
In general, using axiom I is it
![]() (154)
(154)
Multiplying this equation by the stress-energy tensor of general relativity![]() , it is
, it is
![]() (155)
(155)
where γ is Newton’s gravitational “constant” [17] [18] , c is the speed of light in vacuum and π, sometimes referred to as “Archimedes” constant’, is the ratio of a circle’s circumference to its diameter. Due to Einstein’s general relativity, Einstein’s field equations are determined as
![]() (156)
(156)
where Rµv is the Ricci curvature tensor (the trace of Rimanian curvature tensor), R is the scalar curvature, gµv is the metric tensor, Λ is the cosmological constant and Tµv is the stress-energy tensor. Rearranging equation we obtain
![]() (157)
(157)
A commutative [2] division of tensors simplifies the equation as
![]() (158)
(158)
where 1µv denotes the tensor of unified field [2] . In general, a normalization of some tensors of general relativity follows as
![]() (159)
(159)
Quod erat demonstrandum.
3.13. Theorem. The Normalization of the Relationship between the Tensors of the Unified Field Theory
Claim. (Theorem. Proposition. Statement.)
The relationship between the tensors of the unified field theory normalized as
![]() (160)
(160)
Direct proof.
In general, using axiom I is it
![]() (161)
(161)
Multiplying this equation by the energy tensor of general relativity RTµv, it is
![]() (162)
(162)
The field equations of the unified field theory [2] are determined as
![]() (163)
(163)
where RSµv is the tensor of space [2] of the unified field theory and Rtµv is the tensor of time [2] of the unified field theory. Rearranging equation it is
![]() (164)
(164)
A commutative [2] division of tensors simplifies the equation as
![]() (165)
(165)
where 1µv denotes the tensor of unified field [2] . In general, a normalization of some tensors of the unified field theory follows as
![]() (166)
(166)
Quod erat demonstrandum.
3.14. Theorem. The Determination of X
Claim. (Theorem. Proposition. Statement.)
The unknown parameter X, which should equal 1, can be determined as
![]() (167)
(167)
Direct proof.
In general, using axiom I is it
![]() (168)
(168)
Multiplying this equation by the tensor of the unified field 1µv, of the unified field, it is
![]() (169)
(169)
or
![]() (170)
(170)
Due to the theorem about the normalization of some tensors of the unified field theory, this equation rearranges to
![]() (171)
(171)
According to the theorem about the normalization of some tensors of the general theory relativity, the equation before rearranges to
![]() (172)
(172)
A commutative multiplication and division [2] of tensors changes the equation before to
![]() (173)
(173)
Due to our definition, it is ![]() and equally
and equally![]() . Substituting these relationships into the equation before we obtain
. Substituting these relationships into the equation before we obtain
![]() (174)
(174)
Due to commutative operations [2] , this equation can be simplified as
![]() (175)
(175)
which itself can be simplified as
![]() (176)
(176)
or as
![]() (177)
(177)
or as
![]() (178)
(178)
The determination of the value of X follows as
![]() (179)
(179)
Quod erat demonstrandum.
Scholium.
The straightforward question is, must we accept that (RSµv/Rµv) = 1µv or (RSµv/Rµv) = c2 or (RSµv/Rµv) = 1/c2? The probability tensor of the stress-energy tensor of the theory of general relativity is defined as
![]() .
.
The energy tensor of the unified field theory is defined as
![]() .
.
The value of X is determined as (RSµv/Rµv). The equation before changes to as
![]() .
.
In general, the probability tensor is of use to express the energy tensor as
![]() .
.
The probability tensor simplifies this equation simplifies in other word to
![]() .
.
The probability tensor of the tensor ![]() is defined in general something as
is defined in general something as
![]() .
.
The value of X is determined equally as (RSµv/Rµv). The tensor of time
![]()
follows as
![]()
or as
![]()
or as
![]() .
.
In last consequence, the relationship between the field equations of unified field theory and Einstein’s theory of general relativity is determined by the equation
![]() (180)
(180)
or by the equation
![]() (181)
(181)
Einstein’s field equation yields the result
![]() (182)
(182)
What is the physical meaning of Einstein’s field equation, if we multiply the same by the term (1/c2). In this case we obtain
![]() (183)
(183)
In the International System of Units the joule, the unit of energy, is defined as 1[J] = 1[kg∙m2/s2] = 1[N ´ m] while 1[N] = 1[kg∙m/s2] = 1[J/m] denotes the unit of force. The stress-energy tensor Tµv without the mathematical term ![]() has the unit of energy density [J/m3], it is 1[J/m3] = 1[(kg∙m2)/(s2∙m3)]. Let us multiply the stress-energy tensor Tµv by (1/c2), we obtain
has the unit of energy density [J/m3], it is 1[J/m3] = 1[(kg∙m2)/(s2∙m3)]. Let us multiply the stress-energy tensor Tµv by (1/c2), we obtain ![]() which is equivalent with
which is equivalent with![]() . Conse- quently, the term s2 and m2 cancels out and we obtain the unit
. Conse- quently, the term s2 and m2 cancels out and we obtain the unit ![]()
![]() . In other words, the stress-energy tensor Tµv changes to the stress tensor of matter. Thus far, under these conditions there is some evidence that it makes sense to assume that
. In other words, the stress-energy tensor Tµv changes to the stress tensor of matter. Thus far, under these conditions there is some evidence that it makes sense to assume that ![]() [2] . This assumed as correct, the tensor Rgµv [2] is determined as
[2] . This assumed as correct, the tensor Rgµv [2] is determined as ![]() where the term (1/c2) ´ gµv can denote something like the metric tensor of time tgµv = (1/c2) ´ gµv.
where the term (1/c2) ´ gµv can denote something like the metric tensor of time tgµv = (1/c2) ´ gµv.
3.15. Theorem. The Geometrization of the Stress-Energy-Tensor Tµv
In general theory of relativity the gravitational field is completely geometrized. Still, Einstein failed to geometrize the stress-energy-momentum tensor Tµv too. Einstein was convinced that the main problem in the unified field theory was the geometrization of the stress-energy-momentum tensor of matter on the right-hand side of his field equations known to be determined as![]() . The geometrization of the stress-energy-momentum tensor of the matter Tµv should result in the geometrization of the quantum i.e. matter fields.
. The geometrization of the stress-energy-momentum tensor of the matter Tµv should result in the geometrization of the quantum i.e. matter fields.
Claim. (Theorem. Proposition. Statement.)
The total geometrization of all fields or Einstein’s field equations with geometrized stress-energy-momentum tensor of the energy (Tµv) are determined as
![]() (184)
(184)
Direct proof.
In general, using axiom I is it
![]() (185)
(185)
Multiplying this equation by the tensor of the stress-energy tensor ![]() , we do obtain
, we do obtain
![]() (186)
(186)
Due to Einstein’s general theory relativity, this equation can be rearranged as
![]() (187)
(187)
Multiplying Einstein’s field equation by the term (2/R), we obtain
![]() (188)
(188)
Due to our definition, this equation is equivalent with
![]() (189)
(189)
Multiplying the equation before by the term (R/2), Einstein’s field equation completely geometrized follows as
![]() (190)
(190)
Quod erat demonstrandum.
Scholium.
In view of Einstein’s geometrization of gravity, the stress-energy tensor Tµv is the source-term of Einstein’s field equations. From the geometrical point of view, the stress-energy tensor Tµv is still a field without any geometrical significance. In particular, the main goal of the very transparent and also highly general theorem above is to describe matter as an inherent geometrical structure and to incorporate both, the principles of general relativity and quantum theory, in one mathematical formula. Such a theorem is expected to be able to provide a satisfactory (geometrical) description of the microstructure of spacetime, to geometrize the quantum. We rearrange the equation before as
![]() (191)
(191)
or as
![]() (192)
(192)
Einstein’s vacuum field equations can be obtained when the known the stress-energy- momentum tensor is to be determined as (R/2) ´ Egµv = 0. Under these conditions (Tµv = 0), the Einstein vacuum equations are determined by the fact that
![]() (193)
(193)
One focus of this paper is the attempt to build a bridge between quantum theory and classical geometry. The equation before can be changed as
![]() (194)
(194)
In this context we multiply the equation before by the wave-function Ψ. We obtain the Schrödinger’s equation as
![]() (195)
(195)
or a kind of a “normalized” Schrödinger’s equation where R = (![]() ) ~ h/π as
) ~ h/π as
![]() (196)
(196)
an equation where quantum meets geometry and vice versa, where the metric (i.e. geometry) is a determining part of this equation, but the wave-function (i.e. quantum) too. In last consequence, the gravitational field itself can be quantized. A profound methodological challenge for the physicist was the geometrization of the stress-energy tensor Tµv. This problem is solved by this theorem. The mathematical term (R/2) ´ Egµv denotes the geometrical description of the stress-energy tensor Tµv of general theory of relativity. Thus far, in general it is![]() , where Egµv denotes the metric tensor of the stress energy tensor Tµv.
, where Egµv denotes the metric tensor of the stress energy tensor Tµv.
4. Discussion
A new approach to quantum gravity and the unified field theory developed by the author is already published [2] . Besides of the misprint in Equation (76) in [2] , in this paper Equation (197)
![]() (197)
(197)
which should be changed to
![]() (198)
(198)
one way how to geometrize the electromagnetic field is already provided. In this paper the geometrization of the electromagnetic field under conditions of general relativity theory is developed in more (technical) detail. This paper has answered the question about the geometrization of the electromagnetic field under conditions of general theory of relativity.
Thus far, this publication has not answered the question whether does geometrization excludes quantization and vice versa. In other words, is there a dualism between geometrization and quantization in the sense either geometrization or quantization. This geometry-quantum dilemma leads straight forward to the question which came first, the geometry or the quantum? In general, are the rules of quantization more fundamental than the rules of (classical) geometry or vice versa? The question about the very first geometry or the very first quantum also evokes the question of how the development of this universe in general began. Thus far, quantizing geometry is not only a major undertaking but a theoretical necessity and vice versa. Geometrizing the quantum should be provided by a self-consistent deterministic formulation of a unified field theory of nature. In this context, the geometric entity “line” (in the framework of string-theory: the string) is determined by points. But what is a point, how does geometry defines a point? A point appears to be something quantized. In other words, within geometry (a line, a string), the quantum (a point) can be found and surely vice versa. Within the quantum (a point) the geometry (a line) can be found. The one cannot without its own other and vice versa. Today, a unified description of all physical phenomena is endangered especially by the incompatibility between the deterministic geometrical formulation of general relativity and the claimed indeterministic nature of quantum mechanics. Still, the problems of quantizing geometry or geometrizing the quantum are solveable. The answer to such and similar questions may be considered for future work. In this paper, the tensor Dµv was derived as
![]() (199)
(199)
In particular, the physical content of the tensor Dµv is not clear at this moment. Still, a further lack of clarity may not stem from this fact. In order to express the physical content of the tensor Dµv it is necessary to distinguish clearly between the tensor Dµv and the tensor Bµv. To within acceptable margin of error, the information carried by the tensor Dµv is very different from the information as carried by the stress-energy tensor of the electro-magnetic field Bµv. In this context, the tensor Dµv is an anti-tensor of the stress-energy tensor of the electro-magnetic field Bµv. But, as noted above, there are some aspects connected with the tensor Dµv. In fact, the tensor Dµv is a sub-tensor of the metric tensor gµv of Einstein’s gravitational theory of curved spacetime. Thus far, the metric tensor Wgµv has to do something with the gravitational field. Moreover, it is possible and highly desirable that the metric tensor Wgµv is determined by fuctuations of gravitational fields and that the same tensor represents something like “ripples” in spacetime. The interaction between electromagnetic and gravitational waves and the transformation of one wave into another became already a principal focus of theoretical interest and inquiry and has been discussed [22] in literature. Under these assumptions, the tensor Dµv could be determined by the metric tensor of the gravitational waves. More precisely stated, it may be rather difficult to understand the significance that has to be accorded the tensor Dµv but the assumption that the tensor Dµv represents a fourth and until today unknown “force” does not make any sense so far. Despite Einstein’s intent to realize something like a unified field theory, there is considerable disagreement about the extent to which, if at all, such a theory is possible. And yet, from the epistemological standpoint, despite the long history of trials about a completely geometrical field theory of all fundamental interactions under conditions of Einstein’s gravitational theory of curved space-time, it is possible to go beyond general relativities’ definite’ advance in physical knowledge. Furthermore, besides of the influence of Einstein’s reduction of physics to geometry, geometry is nothing absolute but something relative. In fact, striving towards an extension of Einstein’s gravitational theory, we may append an unknown tensor Xµv to Einstein’s filed equations for this purpose. To be sure, the Einstein field equations (EFE) with the extra term Xµv may be written in the form
![]() (200)
(200)
and it follows that
![]() (201)
(201)
More precisely, one possible extension of general relativity is viewed within Table 4.
5. Conclusion
In the 1940s, the theoretical framework of quantum electrodynamics consolidated electromagnetism with quantum physics. It has also to be noted that the trial to geometrize the stress energy tensor or the electromagnetic field within the theoretical framework of general relativity has still not met with much success. In this publication, the stress- energy tensor and the electromagnetic field have been geometrized under conditions of general theory of relativity.
![]()
Table 4. A possible extention of the theory of general realtivity.
Acknowledgements
None.