1. Introduction
The 3D fully analytical calculation of interactions between permanent magnets has been developed since the 1980 years. The first calculations have been made on long shaped magnets in interaction for magnetic bearings. These long magnets can be treated as a 2D problem. In 1984, the first calculation in real analytical 3D has been published for two parallelepiped magnets with parallel magnetizations [1] . The analytical calculation has been continued with perpendicular magnetizations, allowing analytical calculation of interactions with any magnetization direction. More recently, the problem of the analytical calculation of the torque components have been solved [2] [3] [4] .
The analytical calculation can also be used for the energy calculation in a permanent magnet. We will explain how the analytical expression of the energy for a basic parallelepiped magnet is obtained. For more complicated shapes, the calculation can be made by addition of elementary parallelepipeds.
In a permanent magnet, two types of energy are added: the magnetic field energy and the demagnetizing energy. The magnetic field energy is created in the magnet volume, and the demagnetizing energy is linked to the magnet shape. The problem of the energy in a magnet regularly gives scientific discussions [5] [6] . We will explain what term of the energy is calculated by analytical expression. We will compare the results with com- puted data obtained by finite elements method.
2. Basic Mathematical Model
The mathematical model is based on the distribution of magnetic charges on the magnet poles. It is the coulombian representation of the magnetization. The magnet is supposed to be perfect, with its polarization J (in teslas) rigid and uniform, and a relative permeability of 1. The magnet poles can be replaced by distributions of magnetic charges on the poles. Their density σ is defined by:

In Figure 1, since the magnet polarization  is perpendicular to the surfaces 2a × 2b and oriented to the top, the polar faces wear the density σ = +J on the upper face (North Pole), and σ = −J on the lower face (South Pole).
is perpendicular to the surfaces 2a × 2b and oriented to the top, the polar faces wear the density σ = +J on the upper face (North Pole), and σ = −J on the lower face (South Pole).
The magnet centre is O, the origin of the axes Oxyz. Its dimensions are  (Table 1), and its polarization
(Table 1), and its polarization 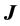 is oriented in the Oz direction.
is oriented in the Oz direction.
The energy calculation is made with four successive analytical integrations. The first one gives a logarithm function. For the second one, two logarithm and two arc-tangent functions are obtained. The integration becomes more difficult at the third integration step. The last one owns many complex functions always based on logarithm and arc- tangent functions.
For all the calculations, the intermediary variables are always:
 (1x)
(1x)
 (1y)
(1y)
![]()
Figure 1. Magnet dimensions and orientation of the polarization J.
![]()
Table 1. Magnet dimensions and parameters.
 (1z)
(1z)
and  (1r)
(1r)
These lengths U, V, W and r correspond to the distance between the parallelepiped corners and their projections on the axes (Equations (1x) to (1r)). The binary parameters i, k, p are equal to 0 or 1 according to the considered corner. For the units, the international system SI is used. The polarization J and the charge density σ are in Tesla [T], and all the lengths are in meters [m]. The energy is calculated in Joule [J].
3. Energy Analytical Calculation
For the integration, the position on the first charged surface is defined by x and y, and the position on the second surface by X and Y. The energy is given by:
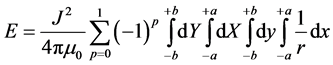
with
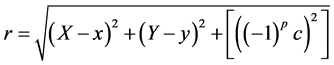 (2)
(2)
After the four integrations, the full analytical expression of the energy can be written by:

with
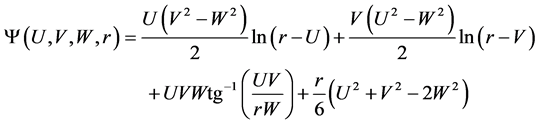 (3)
(3)
The full analytical expression (Equation (3)) is a sum of 8 values of the function y. The function itself is given by classical functions (Napierian logarithm and Arc-tangent) of the geometrical parameters U, V, W and r. The polarization J is included in the
multiplicative factor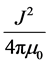 .
.
It can be noted that the magnet energy only depends on the coordinates of the 8 corners of the parallelepiped. Each corner can be seen as a “magnetic node” wearing a contribution of the full energy. A similar approach has been developed for the analytical force calculation between two magnets [2] .
4. Energy in a Permanent Magnet
What is that magnet energy obtained with analytical calculation?
The subject of the energy has produced many discussions because it exist two types of energy in a permanent magnet [5] [6] . In our case, with one perfect permanent magnet alone in the space, it is relatively simple.
4.1. Global Approach of Energy
A global view of a magnet isolated in the space gives:
-The energy in the air outside the magnet is:

The energy “Eair” must be integrated on all the volume around the magnet to obtain the value of the energy outside of the magnet.
-The internal energy inside the magnet “Emagnet” is calculated on all the magnet volume.
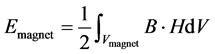
-The energy is always null in the whole volume, magnet and air.

The energy “Eair” is positive and the internal energy inside the magnet “Emagnet” is negative.
4.2. Energy in the Magnet
The magnet energy “Emagnet” is negative because the induction B and field H are opposite inside the magnet.
Using the relation: B = µ0H + J, the energy inside the magnet can be expressed as a function of the magnet polarization J. The magnet energy can be split in two terms:
![]()
The first term is always positive. It is the Magnetic Field Energy “Efield”.
![]()
The second term (1/2J・H) is negative because J and H are opposite. It is often called the Demagnetizing Energy “Edemag”.
![]()
Globally, the magnetic field inside the magnet is linked with the polarization J and the magnet shape by the coefficient N (demagnetizing factor):
![]()
Consequently the Demagnetizing Energy “Edemag” is given by:
![]()
N is the demagnetizing factor. It gives:
![]()
5. Analytical Calculation of the Energy in a Permanent Magnet
The analytically calculated energy corresponds to the interaction energy between the two charged polar surfaces of the magnet. It corresponds to the energy of the charges “-” in the field created by the charges “+”. It should be the “Demagnetizing Energy”.
For verifying the results, three different magnet shapes have been studied. The energy has been calculated by the obtained analytical expressions and by numerical computation with the software FLUX. These last calculations have been made in the air outside the magnet “Eair”, and inside the magnet volume “Emagnet”. The integrals of the terms “1/2B・H” and “1/2J・H” on the magnet volume have also been calculated.
Three magnet dimensions have been studied: 10 × 10 ×![]() 5 mm (half cube), 10 × 10 ×
5 mm (half cube), 10 × 10 ×![]() 10 mm (cube), and 10 × 10 ×
10 mm (cube), and 10 × 10 ×![]() 20 (double cube). The results are presented on Table 2.
20 (double cube). The results are presented on Table 2.
The analytical calculation results are given in the line 1. The numerical calculation has been made inside the magnet “![]() ” (line 2) and outside the magnet “
” (line 2) and outside the magnet “![]() ” (line 3). All the values are in Joule. The terms “1/2B・H” and “1/2J・H” integrated on the magnet volume are shown on line 4 and 5, in italic.
” (line 3). All the values are in Joule. The terms “1/2B・H” and “1/2J・H” integrated on the magnet volume are shown on line 4 and 5, in italic.
The results shown on Table 2 clearly show that:
-The energy inside the magnet “Eanalytic” (line 1), which has been calculated with the analytical expressions, corresponds to the integral on the magnet volume of “1/2J・H” (line 5). It is “Edemag”, one of the two terms of the magnet energy.
-By using the FEM (finite element method) software FLUX, to compute the energy inside the magnet “![]() ”, it is very surprising to obtain a positive value (line 2). In fact, the computed energy is the integral of the term “1/2µ0H2”, the field energy “Efield”.
”, it is very surprising to obtain a positive value (line 2). In fact, the computed energy is the integral of the term “1/2µ0H2”, the field energy “Efield”.
![]()
Table 2. Energy analytically and numerically calculated for three magnet shapes.
The software does not calculate the full magnet energy but one of the two terms of the internal energy. When the magnet is used in a magnetic circuit, the forces are created by the variation of this part of energy.
-The energy in all the air outside of the magnet “![]() ” (line 3) exactly corresponds to the integral of the term “1/2B・H” (line 4).
” (line 3) exactly corresponds to the integral of the term “1/2B・H” (line 4).
-By adding the integral of “1/2J・H” called “Edemag” (line 5), and the “Efield” (line 2), the result exactly corresponds to the integral of “1/2B・H”, the magnet energy “Emagnet”.
6. Interaction Energy
The analytical method has previously been used for the force calculation between two parallelepiped magnets (Figure 2) [1] . The energy between two separated magnets has been calculated with analytical expressions. It has been called “Interaction Energy” because it is the energy of the second magnet placed in the field created by the first magnet. All the interactions like the force components or the torque components can be calculated by derivation of that Interaction Energy.
The Interaction Energy between two magnets is a part of the full energy in the system. It does not take into account the internal energy in each magnet. But when the force or the torque must be obtained, it is not necessary to calculate the full value of the energy, only the variable part of energy is concerned.
7. Synthesis and Conclusions
An original method for calculating the energy in a permanent magnet has been fully developed, using only analytical expressions in 3D. The results obtained with the analytical method have been compared with computed data. The energy calculated with the analytical expression is one term of the internal energy, called the Demagnetizing Energy “Edemag”.
![]()
Figure 2. Interaction between two magnets.
The direct calculation of the magnetic energy with the FEM software FLUX allows calculation of another term of the energy called “Efield”.
The real value of the internal energy can be obtained by integration of “1/2B・H” on the magnet volume. Globally, as the forces and torque components are obtained by energy derivation, calculations can be made with the useful part of the full energy.