Examination of Minimum Time Step, from Modified Heisenberg Uncertainty Principle, Inflaton Physics and Black Hole Physics ()
1. Introduction
First of all we calculate a minimum length, r, and this on the basis of a Poissons equation given in [1] , and then afterwards we will secondly get to calculation of the time step. This is to obtain a Pre inflationary value of the initial time step, 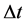 , and then from there we will use an order of magnitude estimate as to the initial mass M of a black hole, to lead to our final conditions.
, and then from there we will use an order of magnitude estimate as to the initial mass M of a black hole, to lead to our final conditions.
2. Modified Poissons Equation [1] Applied to Our Problem
We will first of all refer to two necessary and sufficient conditions for the onset of a massive graviton given in [1] , and combined with Padmanablan’s reference [2] . This heavily borrows from [3] . i.e. what we will be doing is to re do the reference calculations given in [1] with
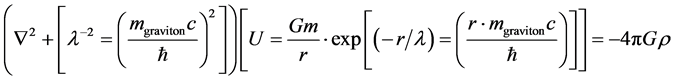 (1)
(1)
Here, we will be using in the Pre-Planckian potential the inputs from the data usually associated with [2]
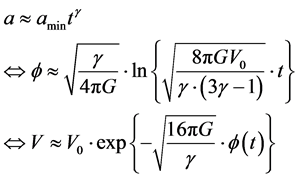 (2)
(2)
In other words, we will be using the inflation given by
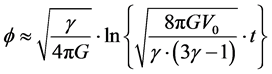 (3)
(3)
If so, then our approximation is to call the Potential in Equation (2) to be the same as U in Equation (1), and then with re arrangements we come up with the following
 (4)
(4)
Then, after algebra, we have the following
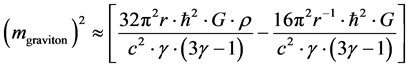 (5)
(5)
The quadratic Equation this engenders is, how to say
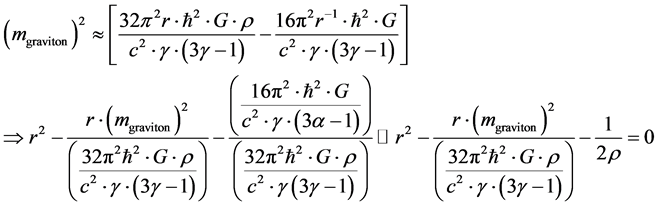 (6)
(6)
We will, in the latter part of this document, associate
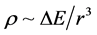 (7)
(7)
And after defining as such work with Equation (7) put into Equation (6) we obtain
 (8)
(8)
We will from here, insert, in the value of 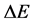 from the HUP given in [3] and also compare it to the work given by Susskind and Hrabovsky in [4] and from there get a linkage of a radial distance, inflaton physics, and a time step
from the HUP given in [3] and also compare it to the work given by Susskind and Hrabovsky in [4] and from there get a linkage of a radial distance, inflaton physics, and a time step .
.
3. HUP, as Used in This Problem
Begin with [3]
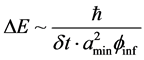 (9)
(9)
In [3] we make the assumption, namely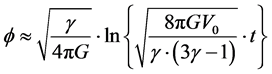 , then Equation (9) becomes
, then Equation (9) becomes
 (10)
(10)
Then
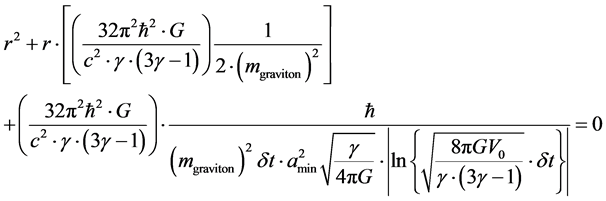 (11)
(11)
This will be further elaborated upon in this document.
4. Examining the Consequences of Equation (10) and Equation (11)
Using the CRC tables, we obtain
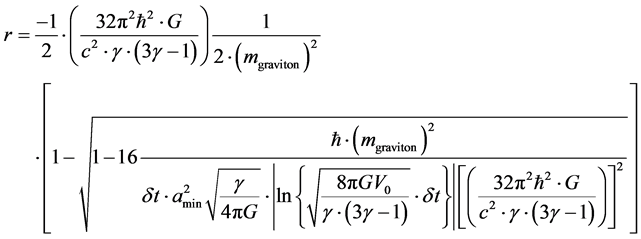 (12)
(12)
Now, then, we can form a force equation, and do it via
 (13)
(13)
The expression ![]() is formed from the inflaton, and we get From Padmanablah, using [1] if
is formed from the inflaton, and we get From Padmanablah, using [1] if![]() , then by [1]
, then by [1]
![]() (14)
(14)
Then, by Equation (13)
![]() (15)
(15)
Now, the time derivative of energy, is [4]
![]() (16)
(16)
Then, if the derivatives dE/dt become instead incremental
![]() (17)
(17)
Then, using ![]()
![]() (18)
(18)
Now, set![]() , and assume in the Pre-Planckian regime, that
, and assume in the Pre-Planckian regime, that ![]()
![]() (19)
(19)
Then Equation (12) becomes
![]() (20)
(20)
We then get a positive r value, and up to a point this is equal to Planck Length ~ 10−33 centimeters
To covert this to time, remove the spatial component on the right hand side of Equation (20) and this is done via
![]() (21)
(21)
We then get a positive r value, and up to a point this is equal to Planck Length ~ 10−33 centimeters
This, above, puts an incredibly tight set of constraints upon the minimum time step. It also assume, that we are looking at a rest mass for the graviton of the order of 10−62 grams. The above Equation (21) is arguing for a peak 1036 Giga Hertz frequency range (1045 Hertz) for relic Gravitational waves, and Gravitons.
5. What Can Be Said Now about the Sciama Black Hole Explosion Idea? (1982)
Sciama [5] in 1982 argued for the lifetime of a black hole, of mass M, that the following holds
![]() (22)
(22)
Here, if the time is about 10−44 seconds (Planck time), then![]() . If so, then, according to [6] , Calmert, et al. about 0.1% of the energy emitted, in the traditional 4 dimensional black hole (3 + 1 dimensions) would be gravitons
. If so, then, according to [6] , Calmert, et al. about 0.1% of the energy emitted, in the traditional 4 dimensional black hole (3 + 1 dimensions) would be gravitons
Then, ![]() becomes linked to Gravitons according to
becomes linked to Gravitons according to
![]() (23)
(23)
This would mean then 1 primordial black hole would produce, if the mass of a graviton is 10−62 grams [7]
![]() (24)
(24)
Assuming there would be say 103 initial primordial black holes, we would then be obtaining 1055 relic gravitons.
Note that if the size of the presumed ![]() expanded, this would lead to a commensurate increase in relic gravitons.
expanded, this would lead to a commensurate increase in relic gravitons.
6. Conclusions
We will, as a start, incorporate Ng’s infinite quantum statistics idea, of entropy being equivalent to a count of particles, i.e. by [8]
![]() (25)
(25)
For relic conditions this implies about 1055 for relic entropy, as opposed to 10120 today for the existing entropy and this also implies an enormously high initial graviton initial frequency a peak 1036 Giga Hertz frequency range (1045 Hertz) for relic Gravitational waves.
Relic graviton frequency, if produced in the beginning of inflation would be by necessity red shifted down, by inflation. i.e. conceivably, if the 1045 Hz was de facto, it may mean present GW of the value of 105 or so, i.e. a 40 magnitude drop in frequency range. i.e. if the generation of GW were at the very start of inflation, it may mean up to a 60 magnitude drop, and a correspondingly enormously low GW frequency. However, the degree of the drop, i.e. say with a 40 magnitude (low end) to a 62 magnitude drop, would say much about a proof about the degree and magnitude of the rapidity of inflation [9] . Which would be of critical import as to cosmology. Having said that there are some serious physical issues to keep in mind while doing this analysis.
Furthermore, we should keep in mind the physics incorporated in [10] [11] i.e. as to the work of LIGO. i.e. it is important to keep in mind that in addition, that [12] has confirmed that a subsequent analysis of the event GW150914 by the LSC constrained the graviton Compton wavelength of those alternative theories of gravity in which the graviton is massive and placed a level of 90\% confidence on the lower bound of 10^{13} km for a Compton wavelength of the graviton. Doing these sort of vetting protocols in line with being consistent with investigation as to a real investigation as to the fundamental nature of gravity. i.e. is this a way to show if general relativity is the final theory of gravitation. i.e., if massive gravity is confirmed, as give n in [13] then GR is perhaps to be replaced by a scalar-tensor theory, as has been shown by Corda.
Refinements of instrumentation may be doable if the nature of the graviton, and its primordial genesis are understood more thoroughly, i.e. as discussed in [14] .
Finally, all this may tie into experimental vetting and confirmation of the work by Corda, as given in [15] , i.e. the nature of the inflaton, as an observed experimental quantity. This in conjunction with refinements in instrumentation brought up in [16] .
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.