Einstein’s Non-Euclidean Line Element Theory and Quantum Mechanics Interpretation ()
1. Probability Concept in Physics
It is the most striking that A. Einstein introduced space-time curvature in general relativity, but wide application of differential geometry in physics made the concept of curvature throughout Newton mechanics, Maxwell’s electromagnetic field theory, the theory of relativity, thermodynamics and quantum mechanics, quantum field theory.
A curve in 3-dimentional Euclid space is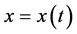 ,
, 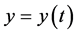 ,
, 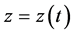 , so
, so 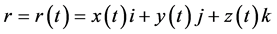 ,
,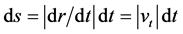 . Let t = s, the absolute value of acceleration relative to parameter s is curvature of curve in space:
. Let t = s, the absolute value of acceleration relative to parameter s is curvature of curve in space: , where speed vector is vertical to acceleration vector. So curvature concept entered into Newton mechanics by this differential geometry expression ( [1] , p. 34). In the 18th and 19th century, after many scholars such as J. L. Lagrange, W. R. Halmiton made efforts, Newton mechanics acquired new forms of analysis mechanics. Maxwell field equations laid the theoretical basis for establishing a special theory of relativity, and it explicitly called the Lorentz transformation. Mathematicians such as Cartan and Hodge, noted that the Maxwell’s equations should be interpreted as a curvature equation of geometric objects known as vector buddle. Maxwell equations led to special relativity naturally, Micheson-Morley experiment led to build light speed constant principle, H. Poincare advanced relativity principle. Einstein explained Lorentz transformation anew, and forced us to receive relativity of simultaneity, and led to H. Minkowski’s 4-dimentional space-time viewpoint.
, where speed vector is vertical to acceleration vector. So curvature concept entered into Newton mechanics by this differential geometry expression ( [1] , p. 34). In the 18th and 19th century, after many scholars such as J. L. Lagrange, W. R. Halmiton made efforts, Newton mechanics acquired new forms of analysis mechanics. Maxwell field equations laid the theoretical basis for establishing a special theory of relativity, and it explicitly called the Lorentz transformation. Mathematicians such as Cartan and Hodge, noted that the Maxwell’s equations should be interpreted as a curvature equation of geometric objects known as vector buddle. Maxwell equations led to special relativity naturally, Micheson-Morley experiment led to build light speed constant principle, H. Poincare advanced relativity principle. Einstein explained Lorentz transformation anew, and forced us to receive relativity of simultaneity, and led to H. Minkowski’s 4-dimentional space-time viewpoint.
Einstein and E. Schrodinger inherit and carry forward Hertz’s basic spirit that builds a new mechanics without “force”. In 1913, in the “outline of general relativity and gravity theory”, Einstein proposed to establish the mathematical theory of general relativity. He points out that the movement of particles, as under the laws of classical mechanics and the theory of special relativity, all meet the principle of least action. In other words, no matter how complicated the geometry of our 4-dimensional world is, light or free particle moves along the geodesic line in it. That is, .
.
Among them, ds2 = gμνdxμdxν, gμν is the metric tensor representation of gravitational field ( [2] , p. 242). Therefore, as long as we put space-time tensor gμν of gravity field in geodesic equation, we can get the equations of motion of particles in the gravitational field:

This is the conclusion of the paper given by Einstein in the “the basis of general relativity” in 1916 ( [2] , p. 319). Among them, Rμν is Riemann curvature tensor, Tμν is material momentum-energy tensor. Because in fact the field equation includes the entire contents of the general theory of relativity, so we can establish the field equation from the least action principle and get the general theory of relativity.
Schrodinger noticed the deep thought relation between Einstein and Hertz, he wrote in 1918 an important manuscript: Hertz mechanics and Einstein’s theory of gravity. He said: “with the help of a clear link between Hertz mechanics and Einstein gravitational theory, I have to point out the importance of this fact, namely in the two theory”, “force” is represented as the same mathematical symbols―the location coordinates of differential mode of flat Riemann three indicator―Christoffel symbols’ ( [3] , p. 522). Just as there is no potential energy in Hertz’s mechanics of the system, the gravitational force is the space-time itself in the general theory of relativity, the degree of curvature of the world line means that the intensity of the gravitational field. As a result, the gravitational field transforms into a sort of geometry. The particle in the gravitational field moves along a geodesic line like a free particle. In these two kinds of theories, the equations of motion make space-time curved, so the world line of the planet is curved. In these two theories, the equations of motion are solved by the path (geodesic), and the only difference lies in the fact that the configuration space of Riemann curvature in Hertz mechanics is generated by the kinetic conditions imposed on the system of implicit motion, and Riemann structure of physical space -time manifold in general relativity is the intrinsic properties of the world geometry.
2. Wave Mechanics and Einstein’s Curvature Tensor Theory of Wave Function
In his “Four Lectures on Wave Mechanics”, Schrodinger thought that Hamilton-Mau- pertuis principle as classical starting point of wave mechanics introduced Heinrich Hertz’s generalized non-Euclidean line element , when we defined a line element in generalized coordinate q space ( [3] , p. 43). And finally we obtained wave equation (or amplitude equation)
, when we defined a line element in generalized coordinate q space ( [3] , p. 43). And finally we obtained wave equation (or amplitude equation)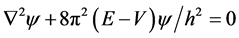 , where
, where 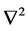 could be regarded as neither a basic Laplacian operator in 3-dimentional space, nor a basic Laplacian operator in high-dimentional space, we should regard it as an extension of Laplacian operator in a line element of generalized coordinate q space ( [3] , pp. 21-22). And all geometry expressions of q space had generalized non-Euclidean line elements’ meaning ( [4] , p. 43). According to Schrodinger’s viewpoint, geometrical optics is only coarse approximate optics, along with wave optics line, we should develop a new wave mechanics in q space. Perhaps our classical mechanics is similar to geometrical optics, as an error, it doesn’t conform to reality. Once curvature radius and route length can compare with a wavelength in q space, classical mechanics becomes invalid. So we seek to a new wave mechanics what starts from Hamilton similarity and find answers along with wave optics line ( [4] , pp. 45-46).
could be regarded as neither a basic Laplacian operator in 3-dimentional space, nor a basic Laplacian operator in high-dimentional space, we should regard it as an extension of Laplacian operator in a line element of generalized coordinate q space ( [3] , pp. 21-22). And all geometry expressions of q space had generalized non-Euclidean line elements’ meaning ( [4] , p. 43). According to Schrodinger’s viewpoint, geometrical optics is only coarse approximate optics, along with wave optics line, we should develop a new wave mechanics in q space. Perhaps our classical mechanics is similar to geometrical optics, as an error, it doesn’t conform to reality. Once curvature radius and route length can compare with a wavelength in q space, classical mechanics becomes invalid. So we seek to a new wave mechanics what starts from Hamilton similarity and find answers along with wave optics line ( [4] , pp. 45-46).
Einstein was inspired by the idea of Schrodinger, and hoped he could restore determinism by a model that integrated wave and particle notions in his note sent to Max Born in April or May of 1927. Einstein published a paper titled “Does Schrodinger’s wave mechanics is to determine the motion of a system or only in the sense of statistics?” on May 5 1927. In this paper, Einstein obtained an expression for kinetic energy using any solution of the Schrodinger equation, and used this to define dq/dt, a velocity component of an individual particle. J. T. Cushing describes in detail how he was able to obtain a unique value for dq/dt in term of the wave-function ψ, using a non-Eucli- dean metric in configuration space in his “Quantum mechanics: Historical Contingency and the Copenhagen Hegemony” published by The University of Chicago Press in 1994 ( [5] , p. 89).
Einstein’s basic idea was that the time-independent Schrodinger equation
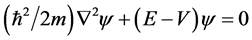
can be used to find the kinetic energy 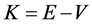 for any given wave function solution ψ defined on an n-dimensional configuration space. He used the quantum-mechanical expression for the kinetic energy
for any given wave function solution ψ defined on an n-dimensional configuration space. He used the quantum-mechanical expression for the kinetic energy 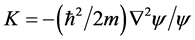 to define an equivalent kinetic energy in point-particle mechanics as
to define an equivalent kinetic energy in point-particle mechanics as .
.
Where gμν is the metric tensor for the configuration space and 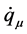 is the velocity component of the particle. These
is the velocity component of the particle. These 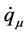 are functions of the configuration-space coordinates (that is, they define a velocity field, the tangents to which are the “flow lines” or possible particle trajectories). Specifically, having set
are functions of the configuration-space coordinates (that is, they define a velocity field, the tangents to which are the “flow lines” or possible particle trajectories). Specifically, having set , where ψμν (which Einstein termed “the tensor of ψ-curvature) is the covariant derivative, he then sought a “unit” vector Aμ
, where ψμν (which Einstein termed “the tensor of ψ-curvature) is the covariant derivative, he then sought a “unit” vector Aμ
![]()
that would render ![]() an extremum. This is the normal curvature of the differential geometry of surfaces. A hermitian quadratic form
an extremum. This is the normal curvature of the differential geometry of surfaces. A hermitian quadratic form ![]() is rendered an extremum by those vectors Aμ that are the solution to the eigenvalue problem
is rendered an extremum by those vectors Aμ that are the solution to the eigenvalue problem![]() .
.
In terms of these Aμ and their eigenvalues λ(α), Einstein was able to give an expression for uniquely assigning the ![]() in terms of a given ψ. (The details of the recipe need not concern us here.) ( [6] , p. 139).
in terms of a given ψ. (The details of the recipe need not concern us here.) ( [6] , p. 139).
Heisenberg wrote a letter to Einstein on 19 May 1927, and expressed a “burning interest” in its subject matter, and Paul Ehrenfest and Max Born had heard about Einstein’s work. However, on May 21 1927, Einstein telephoned the Academy of Sciences of the Academy of Sciences to give up this paper because Walther Bothe raised some objections and doubts ( [7] , pp. 437-438).
The essence of Bother’s objection is that the (covariant) derivative ψμν for such a product wave function ψ = ψ1ψ2 is not zero when μ is an index for referring to the first subsystem and ν one for the second subsystem. That is why the motions of the compound system will not be simply combinations of motions for the subsystems, as Einstein demanded that they be on physical ground ( [6] , p. 139).
In fact, Bothe pointed out that the problem seems to be similar to quantum entanglement, it plays a central role in the later discussion of the EPR paradox, J. S. Bell’s inequality about quantum non-locality and quantum information theory research.
3. Einstein Route of Quantum Mechanics Interpretation
In fact, Einstein’s non-Euclidean line element orbit theory carry out Hertz’s idea that change “minimum principle of action” into “minimum curvature principle” in his “me- chanics principle” in quantum mechanics. Darrin W. Belousek published the thesis “Einstein’s 1927 unpublished hidden variable theory: its background, context and meaning” in studies in history and philosophy of modern physics in 1996 and pointed out: Hertz recognized explicitly the formal analogy between the mechanics of a system of point-particles and the geometry of curved surfaces in multi-dimensional spaces that stands behind his methods. And Einstein too understood this analogy, for (evidently) this is what motivates employing the techniques follow naturally from the introduction of an introduction of a non-Euclidean metric for the multi-dimensional configuration space. But whether Einstein first become acquainted with this method via Schodinger’s paper or has been already familiar with it from Hertz’s mechanics is not known to me ( [7] , p. 444).
“For a system in a stationary state, the ‘tensor of ψ curvature ‘ψμν determines n mutually orthogonal (principle) directions {λ(a)} at each point in the n-dimensional configuration space, and the kinetic energy tensor(expressed in terms of ψμν) determines for each of those directions a velocity component ![]() resultant or vector sum(over a) of which the system’s velocity
resultant or vector sum(over a) of which the system’s velocity![]() . Thus, for each point in the n-dimensional configuration space, ψ determines a unique velocity along the surface at that point. … Now, surfaces in these configuration space are surfaces of a constant phase(S = constant) of the ψ- function,
. Thus, for each point in the n-dimensional configuration space, ψ determines a unique velocity along the surface at that point. … Now, surfaces in these configuration space are surfaces of a constant phase(S = constant) of the ψ- function,![]() . … Hence, the surfaces of constant S can be interpreted as ‘wave fronts’ of the ψ-function propagating in the configuration space according to Schodinger’s wave equation.” ( [7] , pp. 444-445).
. … Hence, the surfaces of constant S can be interpreted as ‘wave fronts’ of the ψ-function propagating in the configuration space according to Schodinger’s wave equation.” ( [7] , pp. 444-445).
“If ψ is not interpreted realistically, then the scheme can most supply a recipe for calculating trajectories in configuration space. If ψ is interpreted realistically, then the scheme can provide a picture in which the motion of a system along such trajectories is determined by causal manner. Here one can view the surfaces of constant S, interpreted as wave fronts of the ψ-function, as ‘guiding’ motions of particles, represented configuration points along those surfaces, via their propagation through configuration space according to Schodinger’s equation. And such an interpretation of ψ would require a postulation of real waves in n-dimensional configuration space in addition to the configuration points that represent states of a system of particles.” ( [7] , p. 445).
Peter Holland published a paper titled “What’s wrong with Einstein’s 1927 hidden variables interpretation of quantum mechanics?” in the “Foundations of physics” (volume 35, April 2005) and pointed out: “We find that the feature Einstein found objectionable―the mutual dependence of the motions of particles when the (many bodies) wave-faction factorises―is indeed a generic feature of his theory” ( [8] , p. 178). “Einstein’s theory (and two modified theories) is flawed, but for reasons not discussed by Einstein (or subsequent commentators); these have to do with the domain of application of the theory, and its relation with empirical prediction.” ( [8] , p. 178).
Einstein tried to make use of generalized coordinates in 3N configuration space as hidden variables to determine generalized velocity uniquely in his 1927 paper, but we often get a pair of opposite directions from the resulting velocity, and they are undetermined eigenspeeds. Einstein linked directions uncertainty of generalized velocities with quasi-periodicity of particle fluctuation, this caused that the non-Euclidean line element representation of quantum mechanics is greatly reduced in the realization of determinism ideal. Einstein does not examine the ability of many body wave mechanics to express independence by using an integrated state; he does not consider quantum entangled state that is suggested in the EPR paper, and Schrodinger pointed out it clearly as ψ’s non-integrable quantum state which involves in non-separability, non-locality and entanglement. Grommer did some adjustments on Einstein’s non-Euclidean line element formulation of wave function, we can guarantee that the product of the wave function of the two combination systems is exactly the wave function of the whole system.
According to Einstein’s Non-Euclidean line element orbital theory, if we calculate the velocity of particle motion, and then we often get wrong velocity eigenvalue. There is a formal parallel between Einstein’s expression for the kinetic energy L and Bohm’s expression for the quantum potential U; but in the de Broglie-Bohm hidden variable theory, if Einstein regarded a physical quantity as kinetic energy, and Bohm regarded this same physical quatity as the quantum potential, thus it can be concluded that the eigenvalue of the particle velocity is consistent with the predictions of quantum mechanics. Therefore, Einstein’s non-Euclidean line element theory’s physical meaning is ambiguous, it might even contain some imaginary velocity components (negative energy), and the same situation also appears in the other two modified versions of Einstein thought proposed by Grommer. D. I. Blokhintsev also payed attention to if we assume that the electrons have certain positions and momentums (even though these values may be unknown and are not observable) when we consider electrons in a Helium atom, then the unexcited electrons can appear in the region above the ground state potential energy, and their kinetic energy becomes negative ( [9] , pp. 190-193).
The constraints on the energy or the domain are entirely artificial in that they do not correspond to any natural requirement of the quantum mechanical treatment in Einstein’s and Grommer’s revised non-Euclidean line element orbit theory. Let us examine a pair of one-dimensional harmonic oscillators of equal frequency ω (![]() ,
,![]() ) in the (product) ground state (
) in the (product) ground state (![]() ):
):![]() , A = constant ( [9] , p. 186).
, A = constant ( [9] , p. 186).
This state does not obey the condition ![]() for all q1, q4. Thus, for Einstein and Grommer’s theory, we obtain for the oscillators [ [9] , p186-187]:
for all q1, q4. Thus, for Einstein and Grommer’s theory, we obtain for the oscillators [ [9] , p186-187]:![]() ,
,![]() . We thus obtain a pair of independent oscillators pursing classical orbits. In this case the orbits are confined to the domain
. We thus obtain a pair of independent oscillators pursing classical orbits. In this case the orbits are confined to the domain ![]() and
and![]() . The origin of the problem of restricted applicability is Einstein’s assumption, rather common in the history of quantum theory, that the quantity E-V appearing in Schodinger’s equation may be regarded as a “kinetic energy”. This assumption, which requires
. The origin of the problem of restricted applicability is Einstein’s assumption, rather common in the history of quantum theory, that the quantity E-V appearing in Schodinger’s equation may be regarded as a “kinetic energy”. This assumption, which requires![]() , is known to lead to paradoxes. It is, in fact, an arbitrary assumption, based on an unjustified allusion to classical mechanics ( [9] , p. 187), and completely ruled out the widespread quantum tunnel effects. It is noteworthy that the development of a trajectory interpretation do not require this assumption.
, is known to lead to paradoxes. It is, in fact, an arbitrary assumption, based on an unjustified allusion to classical mechanics ( [9] , p. 187), and completely ruled out the widespread quantum tunnel effects. It is noteworthy that the development of a trajectory interpretation do not require this assumption.
Peter Holland finds that we can construct an Einstein-type particle coupling theory, and ensure the compatibility with empirical predictions of quantum mechanics. One of the features of this hidden variable theory is: Factorization is only the statistical independence of the system 1 and its environment. In this case, the particle 1 is given a complete physics explanation at the level of hidden variables, involving all hidden variable configurations of the rest of the universe. This means that it is necessary to specify the position of all the particles in the universe before we can calculate the motion of a single particle. This has become a difficult problem to operate in practice, rather than a logic compatibility problem in theory. So, there are mutual dependence of non Euclidean line elements between the two particles even in a quantum integrated state. This is a different correlation of hidden variables from quantum entanglement and quantum non-locality. Modified Einstein-type non-Euclidean line element theory will show stronger quantum wholeness than de Broglie’s guiding wave or Bohm’s quantum potential theory. Just as in general relativity, we need to resort to the whole universe’s material movements distribution and boundary conditions in order to determine mass and space-time metric of an object.
On March 25 in 1935, A. Einstein, D.Podolsky and N.Rosen submitted a paper titled “Can we think quantum mechanics description of physical reality is complete it?” to “Physics Review”, and soon on June 29 in 1935, Niels Bohr submitted a paper of the same name to “Physics Review”. We can find in these two papers that quantum mechanics seems to imply that ( [9] , p. 247): We can not only establish the particle’s wave function by an experiment on a single particle, but also can calculate the wave function of its partner particle without interfering with its partner. Schodinger noticed that quantum mechanics’ characteristic nature is located in this kind of quantum entanglement―“It is exactly this point caused the complete departure from the classical thought course” ( [9] , p. 247). Annihilation photon polarization experiments have showed that an experimenter can really manipulate it into any state of an infinite number of possible states under no interference on condition of a distance system. Schodinger believed that this is not only a theoretical problem, but a serious defect problem in theoretical basis of quantum mechanics. For Einstein, non-locality is a representation of theoretical incomplete description given by ψ-function. Some scholars assume that quantum entanglement can be understood by the wormhole in general relativity, but such a model also caused serious technical difficulties and conceptual difficulties. These wormhole topologies maybe destroy the law of causality, even if there is no connection between the system, space will appear from multiply connected to simply connected topological change after a measurement is completed. ( [10] , pp. 482-483).
In addition to the EPR argument, Einstein also give another argument as a basis for the incompleteness of quantum mechanics that we can’t predict the decay time of a particular atom at any moment. In 1953, Einstein considered a bouncing ball back and forth: According to quantum mechanics, the wave function describes the motion superposition of two opposite velocities, but the ball movement can only be one kind of movement on the macro ( [9] , p. 254). This Einstein’s argument is consistent with the idea of Schodinger’s cat experiment, this shows that we must introduce some incompatible things with the microscopic world of quantum laws in order to get a transition from quantum description to the classical description. As H. Putnam said, Schodinger’s cat experiments show that “the principle that macroscopic observable have a certain value at any time is not derived from the foundation of quantum mechanics, but rather as an additional assumption forces into quantum mechanics.” ( [9] , p. 253). On November 24 in 1954, Einstein wrote a letter to Bohm: “I don’t believe what are the laws of the micro and macro, and only believe the laws in universal framework, and I believe these laws on the logic are simple, the reliance of the logical simplicity is the best guide we have.” ( [9] , p. 254).
4. Conclusion
Einstein’s non-Euclidean line element theory is an early abortion project that he insisted on within the framework of general relativity in the various attempts to solve the quantum problem. For Einstein, when Bohr proposed the hypothesis of the steady state transition of the hydrogen atomic theory in 1913, he did not realize that this assumption and his relativity were in conflict. In 1916, Einstein proposed the theory of stimulated radiation and spontaneous emission of atoms, which became the theoretical basis of laser physics; it was not difficult to see that this theory implicitly contains Bohr’s idea of the steady state transition assumption. But also in this year, Einstein completed his work on creating general relativity; he put the whole physics, especially quantum theory into the framework of general relativity as his own mission. However, Einstein’s non-Euclidean line element theory understands Schodinger equation by Hertz’s “the principle of minimum curvature” that is equivalent to Newton mechanics. Although non-Euclidean line element theory is close to the mathematical model of general relativity in form, but it still adhere to the absolute space-time view of Newton mechanics and particle model in essence. Einstein envisioned a type of field theory like general relativity, if it can’t properly handle many body problems associated with quantum nonlocality and understand what role time play role in quantum measurement, then quantum mystery is hard to solve.
Fund Project
General Research Project of Humanities and Social Science in Chinese Ministry of Edu- cation in 2014: “Philosophy Research in relation between Being and Information in Quantum computing and thermodynamics”, and its Serial Number: 14YJA720004.