The Global Attractors and Their Hausdorff and Fractal Dimensions Estimation for the Higher-Order Nonlinear Kirchhoff-Type Equation with Strong Linear Damping ()
1. Introduction
In this paper, we are concerned with the existence of global attractor and Hausdorff and Fractal dimensions estimation for the following nonlinear Higher-order Kirchhoff-type equations:
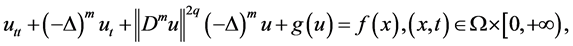 (1.1)
(1.1)
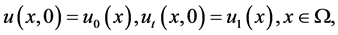 (1.2)
(1.2)
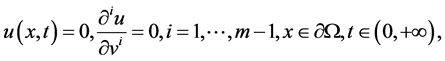 (1.3)
(1.3)
where 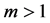 is an integer constant, and
is an integer constant, and 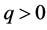 is a positive constant. Moreover,
is a positive constant. Moreover, 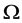 is a bounded domain in
is a bounded domain in 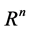 with the smooth boundary
with the smooth boundary 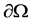 and v is the unit outward normal on
and v is the unit outward normal on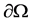 .
. 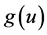 is a nonlinear function specified later.
is a nonlinear function specified later.
Recently, Marina Ghisi and Massimo Gobbino [1] studied spectral gap global solutions for degenerate Kirchhoff equations. Given a continuous function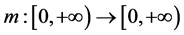 , they consider the Cauchy problem:
, they consider the Cauchy problem:
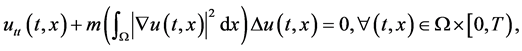 (1.4)
(1.4)
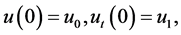 (1.5)
(1.5)
where 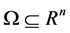 is an open set and
is an open set and 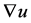 and
and 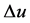 denote the gradient and the Laplacian of u with respect to the space variables. They prove that for such initial data
denote the gradient and the Laplacian of u with respect to the space variables. They prove that for such initial data 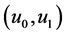 there exist two pairs of initial data
there exist two pairs of initial data ![]() for which the solution is global, and such that
for which the solution is global, and such that ![]()
Yang Zhijian, Ding Pengyan and Lei Li [2] studied Longtime dynamics of the Kirchhoff equations with fractional damping and supercritical nonlinearity:
![]() (1.6)
(1.6)
![]() (1.7)
(1.7)
where![]() ,
, ![]() is a bounded domain
is a bounded domain ![]() with the smooth boundary
with the smooth boundary![]() ,
,
and the nonlinearity ![]() and external force term g will be specified. The main results are focused on the relationships among the growth exponent p of the nonlinearity
and external force term g will be specified. The main results are focused on the relationships among the growth exponent p of the nonlinearity ![]() and well-posedness. They show that (i) even if p is up to the supercritical range,
and well-posedness. They show that (i) even if p is up to the supercritical range,
that is, ![]() , the well-posedness and the longtime behavior of the so-
, the well-posedness and the longtime behavior of the so-
lutions of the equation are of the characters of the parabolic equation; (ii) when
![]() , the corresponding subclass G of the limit solutions exists
, the corresponding subclass G of the limit solutions exists
and possesses a weak global attractor.
Yang Zhijian, Ding Pengyan and Liu Zhiming [3] studied the Global attractor for the Kirchhoff type equations with strong nonlinear damping and supercritical nonlinearity:
![]() (1.8)
(1.8)
![]() (1.9)
(1.9)
where ![]() is a bounded domain in
is a bounded domain in ![]() with the smooth boundary
with the smooth boundary![]() ,
, ![]() ,
, ![]() and
and ![]() are nonlinear functions, and
are nonlinear functions, and ![]() is an external force term. They prove that in strictly positive stiffness factors and supercritical nonlinearity case, there exists a global finite-dimensional attractor in the natural energy space endowed with strong topology.
is an external force term. They prove that in strictly positive stiffness factors and supercritical nonlinearity case, there exists a global finite-dimensional attractor in the natural energy space endowed with strong topology.
Li Fucai [4] studied the global existence and blow-up of solutions for a higher-order nonlinear Kirchhoff-type hyperbolic equation:
![]() (1.10)
(1.10)
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
where![]() ,
, ![]() is a bounded domain
is a bounded domain![]() , with a smooth boundary
, with a smooth boundary ![]() and a unit outer normal v. Setting
and a unit outer normal v. Setting ![]() Assume that p satisfies the condition:
Assume that p satisfies the condition:
![]() (1.13)
(1.13)
Their main results are the two theorems:
Theorem 1. Suppose that ![]() and condition (1.13) holds. Then for any initial data
and condition (1.13) holds. Then for any initial data ![]() the solution of (1.10) - (1.12) exists globally.
the solution of (1.10) - (1.12) exists globally.
Theorem 2. Suppose that ![]() and condition (1.12) holds. Then for any initial data
and condition (1.12) holds. Then for any initial data ![]() the solution of (1.10) - (1.12) blows up at finite time in
the solution of (1.10) - (1.12) blows up at finite time in ![]() norm provided that
norm provided that![]() .
.
Li Yan [5] studied The Asymptotic Behavior of Solutions for a Nonlinear Higher Order Kirchhoff Type Equation:
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
where ![]() is an open bounded set of
is an open bounded set of ![]() with smooth boundary
with smooth boundary ![]() and the unit normal vector. The function
and the unit normal vector. The function ![]() satisfies the following conditions:
satisfies the following conditions:
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
where![]() . Furthermore, there exists
. Furthermore, there exists ![]() such that
such that
![]() (1.19)
(1.19)
At last, Li Yan studied the asymptotic behavior of solutions for problem (1.14) - (1.16).
For the most of the scholars represented by Yang Zhijian have studied all kinds of low order Kirchhoff equations and only a small number of scholars have studied the blow-up and asymptotic behavior of solutions for higher-order Kirchhoff equation. So, in this context, we study the high-order Kirchhoff equation is very meaningful. In order to study the high-order nonlinear Kirchhoff equation with the damping term, we borrow some of Li Yan’s [5] partial assumptions (2.1) - (2.3) for the nonlinear term g in the equation. In order to prove that the lemma 1, we have improved the results from assumptions (2.1) - (2.3) such that![]() . Then, under all assumptions, we prove
. Then, under all assumptions, we prove
that the equation has a unique smooth solution ![]()
and obtain the solution semigroup ![]() has global attractor
has global attractor![]() . Finally, we prove the equation has finite Hausdorff dimensions and Fractal dimensions by reference to the literature [7] .
. Finally, we prove the equation has finite Hausdorff dimensions and Fractal dimensions by reference to the literature [7] .
For more related results we refer the reader to [6] [7] [8] [9] [10] . In order to make these equations more normal, in section 2 and in section 3, some assumptions, notations and the main results are stated. Under these assumptions, we prove the existence and uniqueness of solution, then we obtain the global attractors for the problems (1.1) - (1.3). According to [6] [7] [8] [9] [10] , in section 4, we consider that the global attractor of the above mentioned problems (1.1) - (1.3) has finite Hausdorff dimensions and fractal dimensions.
2. Preliminaries
For convenience, we denote the norm and scalar product in ![]() by
by ![]() and
and![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
According to [5] , we present some assumptions and notations needed in the proof of our results. For this reason, we assume nonlinear term ![]() satisfies that
satisfies that
(H1) Setting ![]() then
then
![]() (2.1)
(2.1)
(H2) If
![]() (2.2)
(2.2)
where ![]()
(H3) There exist constant![]() , such that
, such that
![]() (2.3)
(2.3)
(H4) There exist constant![]() , such that
, such that
![]() (2.4)
(2.4)
![]() (2.5)
(2.5)
where![]() ;
;
For every![]() , by (H1)-(H3) and apply Poincaré inequality, there exist constants
, by (H1)-(H3) and apply Poincaré inequality, there exist constants![]() , such that
, such that
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
where ![]() is independent of
is independent of![]() .
.
Lemma 1. Assume (H1)-(H3) hold, and![]() . Then the solution
. Then the solution ![]() of the problem (1.1) - (1.3) satisfies
of the problem (1.1) - (1.3) satisfies ![]() and
and
![]() (2.8)
(2.8)
where![]() ,
, ![]() ,
, ![]()
is the first eigenvalue of ![]() in
in![]() , and
, and![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() . Thus, there exists
. Thus, there exists ![]() and
and![]() , such that
, such that
![]() (2.9)
(2.9)
Proof. We take the scalar product in ![]() of equation (1.1) with
of equation (1.1) with![]() . Then
. Then
![]() (2.10)
(2.10)
After a computation in (2.10), we have
![]() (2.11)
(2.11)
![]() (2.12)
(2.12)
![]() (2.13)
(2.13)
![]() (2.14)
(2.14)
Collecting with (2.11) - (2.14), we obtain from (2.10) that
![]() (2.15)
(2.15)
Since ![]() and
and
![]() , by using Hölder in-
, by using Hölder in-
equality Young’s inequality and Poincaré inequality, we deal with the terms in (2.15) one by one as follow:
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
By (2.7), we can obtain
![]() (2.18)
(2.18)
where ![]()
Because of![]() , we can obtain
, we can obtain
![]() (2.19)
(2.19)
By (2.16) - (2.19), it follows from that
![]() (2.20)
(2.20)
By Young’s inequality and![]() , we have
, we have
![]() (2.21)
(2.21)
![]() (2.22)
(2.22)
By (2.22), we get
![]() (2.23)
(2.23)
where ![]()
By (2.21) and substituting (2.23) into (2.20), we receive
![]() (2.24)
(2.24)
Since ![]() and
and![]() , we get
, we get
![]() (2.25)
(2.25)
By (2.6) and (2.21), we have
![]() (2.26)
(2.26)
where![]() .
.
Combining with (2.25) and (2.26), formula (2.24) into
![]() (2.27)
(2.27)
We set![]() . Then, (2.27) is simplified as
. Then, (2.27) is simplified as
![]() (2.28)
(2.28)
where ![]()
From conclusion (2.26), we know![]() . So, by Gronwall’s inequality, we obtain
. So, by Gronwall’s inequality, we obtain
![]() (2.29)
(2.29)
where ![]()
By generalized Young’s inequality, we have ![]()
Then, we get
![]() (2.30)
(2.30)
By (2.26) and (2.30), we have
![]() (2.31)
(2.31)
Combining with (2.29) and (2.31),we obtain
![]() (2.32)
(2.32)
Then,
![]() (2.33)
(2.33)
So, there exist ![]() and
and![]() , such that
, such that
![]() (2.34)
(2.34)
Lemma 2. In addition to the assumptions of Lemma 1, (H1) - (H4) hold. If (H5): ![]() , and
, and![]() . Then the solution
. Then the solution ![]() of the pro- blems (1.1) - (1.3) satisfies
of the pro- blems (1.1) - (1.3) satisfies![]() , and
, and
![]() (2.35)
(2.35)
where![]() ,
, ![]() is the first eigenvalue of
is the first eigenvalue of ![]() in
in![]() ,
,
and![]() ,
, ![]() ,
,
![]() . Thus, there exists
. Thus, there exists ![]() and
and![]() , such that
, such that
![]() (2.36)
(2.36)
Proof. Taking L2-inner product by ![]() in (1.1), we have
in (1.1), we have
![]() (2.37)
(2.37)
After a computation in (2.37) one by one, as follow
![]() (2.38)
(2.38)
![]() (2.39)
(2.39)
![]() (2.40)
(2.40)
By Young’s inequality, we get
![]() (2.41)
(2.41)
Next to estimate ![]() in (2.41). By (H4):
in (2.41). By (H4): ![]() and Young’s inequality, we have
and Young’s inequality, we have
![]() (2.42)
(2.42)
By ![]() and Embeding Theorem, then
and Embeding Theorem, then![]() . So there exists
. So there exists
![]() , such that
, such that![]() .
. ![]() bounded by lemma 1. Then, (2.42) turns into
bounded by lemma 1. Then, (2.42) turns into
![]() (2.43)
(2.43)
Collecting with (2.43), from (2.41) we have
![]() (2.44)
(2.44)
By ![]() and Young’s inequality, we obtain
and Young’s inequality, we obtain
![]() (2.45)
(2.45)
Integrating (2.38) - (2.40), (2.44) - (2.45), from (2.37) entails
![]() (2.46)
(2.46)
By Poincaré inequality, such that![]() . So, (2.46) turns into
. So, (2.46) turns into
![]() (2.47)
(2.47)
First, we take proper![]() , such that
, such that ![]() and
and ![]() by Lam- ma 1. Then, we assume that there exists
by Lam- ma 1. Then, we assume that there exists![]() , such that
, such that ![]() and
and
![]() Then, formula is simplified
Then, formula is simplified
to
![]() (2.48)
(2.48)
By Gronwall’s inequality, we get
![]() (2.49)
(2.49)
On account of Lemma 1, we know ![]() is bounded. So the hypothesis is true. Namely, we prove that there are
is bounded. So the hypothesis is true. Namely, we prove that there are![]() , makes
, makes
![]() (2.50)
(2.50)
Substituting (2.50) into (2.47), we receive
![]() (2.51)
(2.51)
Taking![]() , then
, then
![]() (2.52)
(2.52)
where![]() . By Gronwall’s inequality, we have
. By Gronwall’s inequality, we have
![]() (2.53)
(2.53)
where ![]()
Let ![]() so we get
so we get
![]() (2.54)
(2.54)
Then
![]() (2.55)
(2.55)
So, there exists ![]() and
and![]() , such that
, such that
![]() (2.56)
(2.56)
3. Global Attractor
3.1. The Existence and Uniqueness of Solution
Theorem 3.1. Assume (H1) - (H4) hold, and![]() ,
, ![]() ,
,![]() . So Equation (1.1) exists a unique smooth solution
. So Equation (1.1) exists a unique smooth solution
![]() (3.1)
(3.1)
Proof. By the Galerkin method, Lemma 1 and Lemma 2, we can easily obtain the existence of Solutions. Next, we prove the uniqueness of Solutions in detail.
Assume ![]() are two solutions of the problems (1.1) - (1.3), let
are two solutions of the problems (1.1) - (1.3), let![]() , then
, then ![]() and the two equations subtract and obtain
and the two equations subtract and obtain
![]() (3.2)
(3.2)
By multiplying (3.2) by![]() , we get
, we get
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
Exploiting (3.4) - (3.6), we receive
![]() (3.7)
(3.7)
In (3.7), according to Lemma 1 and Lemma 2, such that
![]() (3.8)
(3.8)
where ![]() and
and ![]() are constants.
are constants.
By (H4), we obtain
![]() (3.9)
(3.9)
where ![]() is constant.
is constant.
From the above, we have
![]() (3.10)
(3.10)
For (3.10), because ![]() is bounded. Then, there exists
is bounded. Then, there exists![]() , such that
, such that ![]() . So, we have
. So, we have
![]() (3.11)
(3.11)
where ![]() By using Gron-
By using Gron-
wall’s inequality for (3.11), we obtain
![]() (3.12)
(3.12)
Hence , we can get ![]() That shows that
That shows that
![]() (3.13)
(3.13)
That is
![]() (3.14)
(3.14)
Therefore
![]() (3.15)
(3.15)
So we get the uniqueness of the solution.
3.2. Global Attractor
Theorem 3.2. [10] Let E be a Banach space, and ![]() are the semigroup operator on E.
are the semigroup operator on E.![]() , where I is a unit operator.Set
, where I is a unit operator.Set ![]() satisfy the follow conditions:
satisfy the follow conditions:
1) ![]() is uniformly bounded, namely
is uniformly bounded, namely![]() , it exists a constant
, it exists a constant![]() , so that
, so that
![]() (3.16)
(3.16)
2) It exists a bounded absorbing set![]() , namely,
, namely, ![]() , it exists a constant
, it exists a constant![]() , so that
, so that
![]() (3.17)
(3.17)
where ![]() and
and ![]() are bounded sets.
are bounded sets.
3) When![]() ,
, ![]() is a completely continuous operator. Therefore, the semigroup operator S(t) exists a compact global attractor
is a completely continuous operator. Therefore, the semigroup operator S(t) exists a compact global attractor![]() .
.
Theorem 3.3. Under the assume of Lemma 1, Lemma 2 and Theorem 3.1, equations have global attractor
![]() (3.18)
(3.18)
where![]() ,
, ![]()
is the bounded absorbing set of ![]() and satisfies
and satisfies
1)![]() ;
;
2)![]() , here
, here ![]() and it is a bounded set,
and it is a bounded set,
![]() (3.19)
(3.19)
Proof. Under the conditions of Theorem 3.1, it exists the solution semigroup S(t), ![]() , here
, here![]() .
.
(1) From Lemma 1 to Lemma 2, we can get that ![]() is a bounded set that includes in the ball
is a bounded set that includes in the ball![]() ,
,
![]() (3.20)
(3.20)
This shows that ![]() is uniformly bounded in
is uniformly bounded in![]() .
.
(2) Furthermore, for any![]() , when
, when![]() , we have
, we have
![]() (3.21)
(3.21)
So we get ![]() is the bounded absorbing set.
is the bounded absorbing set.
(3) Since ![]() is compact embedded, which means that the bounded set in
is compact embedded, which means that the bounded set in ![]() is the compact set in
is the compact set in![]() , so the semigroup operator S(t) exists a compact global attractor
, so the semigroup operator S(t) exists a compact global attractor![]() .
.
4. The Estimates of the Upper Bounds of Hausdorff and Fractal Dimensions for the Global Attractor
We rewrite the problems (1.1) - (1.3):
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
Let![]() , where
, where ![]() is a bounded domain in
is a bounded domain in ![]() with smooth boundary
with smooth boundary![]() , q is positive constant, and m is positive integer. The linearized equations of the above equations as follows:
, q is positive constant, and m is positive integer. The linearized equations of the above equations as follows:
![]() (4.4)
(4.4)
![]() (4.5)
(4.5)
Let![]() ,
, ![]() is the solution of problems (4.4) - (4.5). We can prove that the problems (4.4) - (4.5) have a unique solution
is the solution of problems (4.4) - (4.5). We can prove that the problems (4.4) - (4.5) have a unique solution ![]() The equation (4.4) is the linearized equation by the Equation (4.17). Define the
The equation (4.4) is the linearized equation by the Equation (4.17). Define the
mapping![]() , here
, here![]() , let
, let![]() ,
,
![]() , let
, let![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() .
.
Lemma 4.1 [6] Assume H is a Hilbert space, ![]() is a compact set of H.
is a compact set of H. ![]() is a continuous mapping, satisfy the follow conditions.
is a continuous mapping, satisfy the follow conditions.
1)![]() ;
;
2) If ![]() is Fréchet differentiable, it exists is a bounded linear differential operator
is Fréchet differentiable, it exists is a bounded linear differential operator![]() , that is
, that is
![]()
The proof of lemma 4.1 see ref. [6] is omitted here. According to Lemma 4.1, we can get the following theorem :
Theorem 4.1. [6] [7] Let ![]() is the global attractor that we obtain in section 3.In that case,
is the global attractor that we obtain in section 3.In that case, ![]() has finite Hausdorff dimensions and Fractal dimensions in
has finite Hausdorff dimensions and Fractal dimensions in
![]() ,that is
,that is![]() .
.
Let![]() , let
, let![]() , is an isomorphic mapping. So let
, is an isomorphic mapping. So let ![]() is the global attractor of
is the global attractor of![]() , then
, then ![]() is also the global attractor of
is also the global attractor of![]() , and they have the same dimensions. Then
, and they have the same dimensions. Then ![]() satisfies as follows:
satisfies as follows:
![]() (4.6)
(4.6)
![]() (4.7)
(4.7)
where ![]()
![]() (4.8)
(4.8)
![]() (4.9)
(4.9)
![]() (4.10)
(4.10)
![]() (4.11)
(4.11)
where![]() . The initial condition (4.5) can be written in the following form:
. The initial condition (4.5) can be written in the following form:
![]() (4.12)
(4.12)
We take![]() , then consider the corresponding n solutions:
, then consider the corresponding n solutions: ![]() of the initial values:
of the initial values: ![]() in the Equations (4.10) - (4.11). So there is
in the Equations (4.10) - (4.11). So there is
![]() . from
. from
![]() , we get
, we get ![]()
![]() , here u is the solution of problems (4.1)-(4.3);
, here u is the solution of problems (4.1)-(4.3); ![]() represents the outer product, Tr reprsents the trace,
represents the outer product, Tr reprsents the trace, ![]() is an orthogonal projection from the space
is an orthogonal projection from the space ![]() to the subspace spanned by
to the subspace spanned by![]() .
.
For a given time![]() , let
, let![]() .
. ![]() is the
is the
standard orthogonal basis of the space![]() .
.
From the above, we have
![]() (4.13)
(4.13)
where ![]() is the inner product in
is the inner product in![]() .Then
.Then![]() ;
; ![]() .
.
![]() (4.14)
(4.14)
where
![]()
Now, suppose that![]() , according to theorem 3.3,
, according to theorem 3.3, ![]() is a bounded absorbing set in
is a bounded absorbing set in![]() .
.![]() .
.
Then there is a ![]() to make the mapping
to make the mapping![]() . At the same time, there are the following results:
. At the same time, there are the following results:
![]() (4.15)
(4.15)
where ![]() meets:
meets:![]() . Comprehensive above can be obtained:
. Comprehensive above can be obtained:
![]() (4.16)
(4.16)
![]() , due to
, due to ![]() is a standard orthogonal basis in
is a standard orthogonal basis in![]() . So
. So
![]() (4.17)
(4.17)
Almost to all t, making
![]() (4.18)
(4.18)
So
![]() (4.19)
(4.19)
Let us assume that![]() , is equivalent to
, is equivalent to ![]() Then
Then
![]() (4.20)
(4.20)
According to (4.19), (4.20), so
![]() (4.21)
(4.21)
Therefore, the Lyapunov exponent of ![]() (or
(or![]() ) is uniformly bounded.
) is uniformly bounded.
![]() (4.22)
(4.22)
From what has been discussed above, it exists![]() , a and r are constants, then
, a and r are constants, then
![]() (4.23)
(4.23)
![]() (4.24)
(4.24)
![]() (4.25)
(4.25)
![]() (4.26)
(4.26)
According to the reference [6] [7] , we immediately to the Hausdorff dimension and fractal dimension are respectively![]() .
.
5. Conclusion
In this paper, we prove that the higher-order nonlinear Kirchhoff equation with linear damping in ![]() has a unique smooth solution
has a unique smooth solution![]() . Fur- ther, we obtain the solution semigroup
. Fur- ther, we obtain the solution semigroup ![]() has global attractor
has global attractor![]() . Finally, we prove the equation has finite Hausdorff dimensions and Fractal dimensions in
. Finally, we prove the equation has finite Hausdorff dimensions and Fractal dimensions in![]() .
.
Acknowledgements
The authors express their sincere thanks to the aonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper.
Fund
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11561076.