A Note on the Relationship between the Pearson Product-Moment and the Spearman Rank-Based Coefficients of Correlation ()
1. Introduction
The Pearson product-moment coefficient of correlation can be interpreted as the cosine of the angle between variable vectors in n dimensional space (e.g. [1] and [ [2] , p. 702]). Pearson [3] showed that the relationship of turning Spearman rank-based correlation coefficients (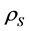 ) for the bivariate normal distribution into Pearson product-moment correlations (
) for the bivariate normal distribution into Pearson product-moment correlations ( ), which was contrived based on the so-called correlation of grades, for large samples to be:
), which was contrived based on the so-called correlation of grades, for large samples to be:
 (1)
(1)
For finite (small) samples, Moran [4] derived the relationship between the Pearson and Spearman coefficients of correlation for the bivariate normal distribution, which also appears in Headrick [ [5] p. 114], to be:
 . (2)
. (2)
Taking the limit as  in Equation (2) will reduce Equation (2) to Equation (1). We would also note that Höffding [6] demonstrated that the Spearman rank correlation tends to normality for any given parent population.
in Equation (2) will reduce Equation (2) to Equation (1). We would also note that Höffding [6] demonstrated that the Spearman rank correlation tends to normality for any given parent population.
2. Mathematical Development
In view of the above, this note derives the relationship between the Pearson product-moment correlation coefficient and the Spearman rank-based correlation coefficient for the bivariate normal distribution, in a different manner from either the Pearson [3] or the Moran [4] derivations, through the following infinite cosine series:
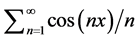 . (3)
. (3)
Specifically, if we let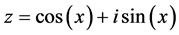 , then
, then
 (4)
(4)
where it follows that for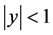 , that
, that
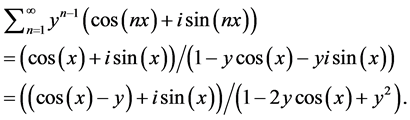 (5)
(5)
Thus, from Equation (5) we have:
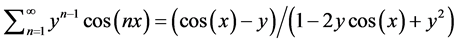 . (6)
. (6)
The series associated with Equation (6) is uniformly convergent for all values of y and for . As such, integrating with respect to y, where
. As such, integrating with respect to y, where  yields:
yields:
 (7)
(7)
Let x neither be zero nor a multiple of . As such, it necessarily follows that the series in Equation (3) is convergent. Hence, for
. As such, it necessarily follows that the series in Equation (3) is convergent. Hence, for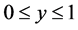 ;
;  is positive, monotonic, decreasing, and bounded. Whence, the series
is positive, monotonic, decreasing, and bounded. Whence, the series
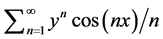 (8)
(8)
is, therefore, uniformly convergent for![]() . Subsequently letting
. Subsequently letting![]() , noting again that x is neither zero nor a multiple of
, noting again that x is neither zero nor a multiple of![]() , it follows that Equation (3) can be expressed as
, it follows that Equation (3) can be expressed as
![]() . (9)
. (9)
3. Main Result and Conclusions
Setting ![]() in Equation (9), and through subsequent inverse exponentiation
in Equation (9), and through subsequent inverse exponentiation ![]() of Equation (9), yields the relationship (for large samples) between the Pearson product-moment correlation and the Spearman rank-based correlation coefficients as
of Equation (9), yields the relationship (for large samples) between the Pearson product-moment correlation and the Spearman rank-based correlation coefficients as
![]() (10)
(10)
for the bivariate normal distribution. In conclusion, the algorithm provided below in Equation (11), which has an oscillating effect of the Gibbs phenomenon [7] , to demonstrate the analytical derivation above is given as:
![]() (11)
(11)
where![]() , k is finite, and where Equation (11) converges to Equation (10) as
, k is finite, and where Equation (11) converges to Equation (10) as![]() . Finally, in terms of the error associated with Equation (11), it is straight-for- ward to see through real analysis, that
. Finally, in terms of the error associated with Equation (11), it is straight-for- ward to see through real analysis, that ![]() and
and ![]() have a maximum absolute deviation when
have a maximum absolute deviation when ![]() and hence Equation (10) would result in
and hence Equation (10) would result in![]() . As such, at this maximum point of deviation, given that
. As such, at this maximum point of deviation, given that ![]() in Equation (11), that the absolute error is less than
in Equation (11), that the absolute error is less than ![]() when juxtaposed with Equation (10).
when juxtaposed with Equation (10).