Impact of the Objective Function on the Construction of Internal Grids of Wind Farms Using Genetic Algorithm ()
1. Introduction
The world is facing huge challenges, such as the need to increase the supply of energy, reduce the emission of greenhouse gases, and guarantee production and consumption efficiency. It is necessary to reduce energy waste. Therefore, the evolution of wind energy during the last years in Brazil is highly significant. It has moved from 237 GWh in 2006 to 12,210 GWh in 2014 [1] . The expectation is that 10% of the energy generated in the country will come from wind sources until 2020. The continuous reduction of investment costs for its construction may reduce input costs for building, which has a highly energy-dependent production process. It may also reduce costs for cement and aluminum industries, whose main input is energy. This would benefit the productive chain of the construction industry macro complex, leading to higher competitiveness and sustainability.
The use of wind to generate energy in large scale is obtained through the installation of several wind generators on a site, forming a wind power plant. From now on, wind power plant will be called wind farm. This solution proved to be technically and economically viable [2] and it is implemented in the whole world, with the construction of wind farms connected to the electrical grid. As a result, the spread of this source of energy is promoted.
The spread of wind energy in Brazil leads to the development of the civil work industry. It happens because the deployment of a wind farm involves the construction of roads, crane mounting platforms, foundations for wind generators’ towers, trenches and crossings for the plant’s internal medium voltage distribution grid, control station, substation, and transmission line for connecting to the electrical grid. Civil engineering is also strongly affected by the evolution and innovation of wind energy due to the new technologies for building concrete towers.
The plant’s internal medium voltage distribution grid will from now on be called internal grid. Finding the optimum technical and economical configuration for an internal grid involves multiple factors such as: the sizing of the circuits using the ampacity of conductors and voltage drop criteria, calculation of the optimum cable, cost of the initial investment for constructing the facilities, cost of electrical losses during the project horizon, among others. Different configurations can be defined depending on the criterion adopted for sizing the internal grid. The main purpose of this article is to analyze the influence of these criteria in the construction of the internal grid’s facilities.
The design of an internal grid of a wind farm consists essentially in defining its best topology and sizing. Stipulating the internal grids’ topology is a problem of large-scale combinatorial optimization, due to the high number of possible network configurations. This problem is not easily solved. Interactive methods must be applied. Its results converge to an optimum feasible solution.
The use of optimization techniques in the construction industry design reduces the costs of deploying the network and reduces the energy cost. It benefits the energy-in- tensive macro complex of the construction industry. It also contributes to increase building efficiency, which still needs to be improved in Brazil.
Therefore, different mathematical programming techniques were proposed in [4] [5] [6] for solving several problems regarding the expansion of distribution networks. The techniques have proved to be adequate to the discreet nature of the problem and to the complexity and non-linearity of the objective functions.
The development of new techniques that allow genetic algorithms (GAs) to configure large-scale networks in a feasible time period is shown in [7] . In [8] , we present a comparative study for optimizing cables using conventional methodology and a methodology based on genetic algorithm. The purpose was to minimize losses, maintaining voltages within acceptable limits. In [9] , we propose a method for reconfiguring the distribution network aiming at cost reduction and increased reliability.
In the wind farm collector network proposed in [3] , a genetic algorithm optimizes the resources during the planning phase of a wind farm’s internal grid. In [10] , we present a search approach for the best electrical grid design for offshore wind plants. It uses an improved genetic algorithm that considers different sections of the cables when designing the radial arrays. As wind energy recovery in offshore farms becomes more interesting, attention must be brought to economic aspects of electric system, as affirm [11] who proposed an optimization model based on real analysis of offshore wind farms and on the investment cost of electric components.
The use of AG to solve collection grid optimization problem has been discussed in [12] , in which the main advantages of the proposed method had been highlighted. The method considered all the connection topologies of wind turbines (radial, tree, star and ring) and prohibited crosses between subsea cables. The fitness function aims to minimize collection grid cables costs. The radial topology was the one which resulted in the best solution. Authors highlighted that this topology showed the best arrangement in terms of investment cost. Also optimization methods of offshore wind farm grids have been proposed in [13] [14] .
In this paper, we analyze the influence of the different sizing criteria on the optimized configuration of a wind farm’s internal grid, using a methodology based of genetic algorithm (GA).
The use of optimization method based on AG has many advantageous since they show good responses for discrete problems, non-linear objective functions and for very complex computational problems.
The novelty proposed in the present study, which is taking into consideration the cables selection in the fitness function, reduces the space in which the solutions are searched. Similarly, the definition of economic track of the cables in the beginning of the problem improved AG performance, since cable test for each suggested topology can be avoided, reducing therefore computational effort.
Comparative analysis of the various design criteria of the internal grid, changing objective function portions, enables the assessment of the influence of each criterion in the solution of the topology grid.
Grid sensitivity degree can be identified when analyzing different solutions for the objective function, i.e. minimal distance, electric losses and economic aspects. This analysis enables the determination of the influence of the optimal cable methodology use and also the identification of the most appropriate criterion according to the objective function of interest.
2. Mathematical Modeling
The problem in calculating a wind farm’s collector system is mainly finding an ideal radial configuration that connects a set of wind generators with minimal investments in construction and operating costs, considering the pre-defined technical requirements.
Since GAs perform a blind search, a guide is needed to orient them toward the optimum solution. Therefore, it is necessary to find a function to lead the GA in the solution of the problem. To define a function reflecting the objectives that need to be achieved for solving the problem, mathematical modeling is needed.
According to [15] , the problems can be addressed by optimizing one or more objective functions. In addition, according to the author, the problems can be modeled considering technical and economic constraints, or other factors. According to [16] , this function is the method used by the GA to determine the quality of an individual as a solution for the problem.
According to [17] , the objective function of an optimization problem is built from the parameters involved in the problem. It provides a measure of the closeness of the solution in relation to a set of parameters. The objective is to find the optimum point, which is the minimization of this function.
For this treatment, the problem will consider wind generators and the substation with their geographic locations. This will be done in order to enable the calculation of distances, where each point is composed by a coordinate (x, y). Thus, a hypothetical situation of a wind farm is shown in Figure 1, where the circles stand for wind generators and the triangle stands for the substation.
![]()
Figure 1. Position of wind generators and substation of a fictitious wind farm with a feasible configuration of the collector network.
An encompassing modeling that considers the investment cost and the operational costs is needed in order to find the optimum solution for the network. It is needed because it enables the analysis of the parameters’ influence, using parts of the objective function for defining configurations. Therefore, the following formulation is employed to find the best radial topology that connects all the wind generators to the substation. The purpose is to minimize the deployment costs so that the sum of the deployment costs and the present value of energy losses in a planned horizon is as small as possible:
 (1)
(1)
where r is a configuration of the plant’s internal grid and Cr is the set of all feasible related radial configurations. Feasible configurations are considered to be those in which the power flow in the sections is compatible with the maximum ampacity of conductors while also meeting the criteria of established voltage drop and the economical sizing of the cable.
To meet the objective proposed, the function f(r) of the formula (1) is defined as:
 (2)
(2)
where,
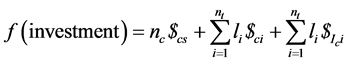 (3)
(3)
and,
 (4)
(4)
Thus, according to expression (2):
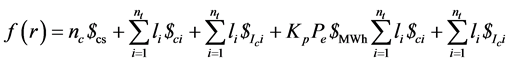 (5)
(5)
where:
nc: number of circuits;
$cs: cost per cubicle of connection substation to each circuit;
li: length of the section i (km);
$ci: cost per km of cable to be installed in section i;
nt: number of sections of the internal distribution network;
$Ici: cost per km of installation of cable to be deployed in section i;
kp: loss factor due to daily and seasonal variations;
Pe: energy losses in internal grid (MWh/year);
$MWh: cost of energy (R$/MWh);
i: correction rate p.y.;
A: number of years in the planning horizon of the design.
The f(r) function shows the costs of the collector network deployment and their respective circuit receiving panels in the substation, and the operating costs.
Thus, minimizing the f(r) function means finding the most economical solution to the internal grid of the wind farm. It must consider not only for the implementation costs, but also the associated operating costs of reducing energy losses over the project horizon.
Two fixed costs per circuit are considered when calculating the implementation of the internal grid: the cost of the cubicles and the cost related to the deployment of each section of the collector network. The first cost, concerning each section of the network, is the cost of the cable itself. It will be selected from a family of candidate conductors eligible by supportability, impedances, and cost per kilometer. The second is the construction cost per kilometer. It depends on the type of installation considering possible facilities established.
The costs of the wind generators’ medium voltage cubicles are not considered since they are already being considered in the costs of the turbines’ electrical system. In addition, they are irrelevant for comparing alternatives, since this cost is the same for every alternative.
The present value of the losses is calculated from the total energy losses of the first- year. It is done by applying the annual rate of correction to the losses of the following years, until the horizon of the project. This calculation assumes that the wind generators operate within their limits. The loss factor kp is present in the formula, repre- senting the daily and seasonal wind variations in the project area.
3. Genetic Algorithm for Setting up the Network
A methodology based on GA, with a chromosome coding by edge using binary numbers, is proposed for solving this problem.
Genetic crossover and mutation special operators are used. The stop is given when the maximum generation number is reached or when a population does not improve in successive generations. To preserve the characteristics of the best individual solution in the next generation, the proposed GA also uses elitism. In the end, the algorithm provides the topology to be built and the costs.
This section is divided in four subsections: the first two subsections show the encoding and decoding proposal. The third subsection shows the approach that makes up the special functions of the GA. Finally, the fitness function is described in the fourth subsection.
3.1. Coding Scheme
The topology of a collector network is modeled in graphs. An example of a small fictive wind farm containing a substation and three wind generators is demonstrated, as in Figure 2. The substation is represented by the solid triangle, the wind generators by solid black circles, and edges are numbered from 1 to 6. Figure 3 shows a feasible collector network configuration for this example.
The individual encoding of the network to the topology of Figure 3 will have the chromosome presented in Figure 4. This is done in order to establish a coding edge
![]()
Figure 2. Largest possible number of edges of a fictitious wind farm.
![]()
Figure 3. A feasible topology for the example system.
![]()
Figure 4. Codification of the internal grid topology in Figure 3.
with binary numbers for the genetic model example of the fictitious wind farm, where there is only a single substation node and three generator nodes.
In Figure 4, the chromosome that encodes the internal grid is highlighted by a gray background. It has a length equal to the maximum possible number of edges. Above each gene, there are their respective maximum limits. In the bottom line, there are the identifiers of the edges associated with each gene. The ceiling of each chromosome gene corresponds to the binary numbers (0 and 1), where 0 means off-edge and 1 means edge-connected.
By adopting this definition, the GA considers that the edge encoded with 0 “does not exist” in this topology and the edge with 1 “exists”. The network topology is drawn accordingly.
In the encoding defined for the chromosome, each gene represents an edge. Thus, edges 3, 4 and 5 have gene number 0 and are not part of this solution to the network. Only the edges with gene number 1 are considered, which are edges 1, 2 and 6. It shows the adhesion of chromosome encoding for the topology of Figure 3. It is important to note that in this example the chromosome size is 6, equal to the number of possible edges for this example, as seen in Figure 2.
3.2. Decoding
Decoding adopts the premise that all the edges are turned off or do not exist (code 0). Taking the decoding of the individual Figure 4 as an example, the procedure is to go to each chromosome, in any order. When the gene number 1 is found, a new edge is created. Thus, taking the second element of Figure 4, A (2) = 1, associated with edge 2 as the gene is encoded with the number 1, this edge is created connecting the substation node 0 to generator node 2. Therefore, all edges with gene number 1 will be created, and edges with gene number 0 will be disregarded.
As seen, decoding is direct. The procedure is repeated for each gene, resulting in the creation of the three edges represented in Figure 3.
3.3. Special Features of the Proposed GA
In the proposed algorithm, special features were created in the generation of the initial population, and in the crossover and mutation operators. It modified them to create only radial and connected individuals. In the generation of the initial population, a heuristic of only creating radial and connected individuals were deployed. Similarly, when there is crossover and mutation, new individuals are tested for connectivity and radial configuration. It ensures that all individuals of the new population are radial and connected.
3.4. Methodology for Calculating the Fitness Function
The fitness function determines the value of each individual in the population. This function measures how close a particular solution (individual) is to the desired solution. The algorithm performs a blind search, guided exclusively by this function.
The objective function defined in Equation (5) covers the objectives set out in this article. Fitness includes the objective function, and also sizes and calculates the components and the network parameters necessary for the assessment of the population.
Initially, the economic calculation of the cable is made in order to define the current ranges of the family of competitor cables outside the GA. The upper and lower limits of the current in amperes for the economic range of a given conductor section are calculated by the following equations [18] :
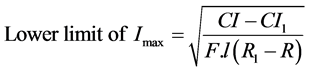 (A) (6)
(A) (6)
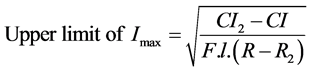 (A) (7)
(A) (7)
where:
CI is the cost of cable length installation, whose section is being considered, expressed as a unit of currency (R$);
R is the a.c. resistance per unit length of the cable section being considered, expressed in ohms per meter (Ω/m);
Cl1 is the cost of installing the next lower cable nominal section, expressed in currency unit ($);
R1 is the a.c. resistance per unit length of the next lower cable nominal section, expressed in ohms per meter (Ω/m);
CI2 is the cost of installing the next larger cable of nominal section, expressed in currency unit ($);
R2 is the a.c. resistance per unit length of the next larger nominal cable section, expressed in ohms per meter (Ω/m).
Therefore, knowing the currents in the sections, the GA sets the optimum cable for each section based on the current ranges established in the economic calculation of the cable. Table 1 shows the fitness calculation methodology that assesses individuals.
![]()
Table 1. Methodology of fitness calculation.
4. Case Analysis
In this section, we analyze the configuration of the internal grid for different alternatives considering the different objectives of the problem. This is achieved by modifying the objective function and the restrictions imposed to the solution of the problem.
4.1. Wind Farm Analyzed
The example system of the wind farm used for the analysis is the one presented in Figure 5, obtained in [3] . In this system, the substation is represented by the solid triangle and the wind generators are represented by the solid circles. The system is composed by the wind farm with fifteen (15) wind generators and 2 MW rated power.
The features of the wind farm [3] are presented bellow.
Internal grid voltage 34.5 kV;
Cost per cubicle feeder output: R$ 100,000.00;
Typical loss factor for the studied region: 0.21;
Energy cost: R$ 200.00/MWh;
Annual correction rate: 11%;
Planning horizon: 20 years.
![]()
Figure 5. Spatial arrangement of example wind farm.
The wind generators and the substation geographic locations are presented in Table 2 and in Figure 5. The data on the cables/structures used in the study are presented in Table 3.
Different propositions can be made for the optimization of the internal grid of the wind farm depending on the objectives pursued. On the one hand, the internal grid can be set with the purpose of finding the best technical and economical solution considering investment and operational costs, and also meeting the technical restrictions of the problem. On the other hand, the configuration of the internal grid of the wind farm can be defined considering the investment and the operational costs separately. Similarly, it may not be desirable for the solution to contain the calculation of the optimal cable in the sections. This is because it directly influences investment and operational costs. All this alternatives are achieved modifying the objective function. Table 4 presents the main cases considering the objectives pursued in the definition of the internal grid.
In Table 4, Capex are the investment costs and Opex are the operational costs. In the application of the model proposed based on GA, the objective function defined in Equation (5) was adopted for Cases 1 and 5. For Cases 2 and 6, the objective function is represented by Equation (3). For the Cases 3 and 7, Equation (4) defines the objective function.
Equations (6) and (7) are used to define the current ranges of the cables in cases where the fitness function considers the calculation of the optimum cable in each section of the internal grid. In cases where the best solution for the distance is searched, the objective function guides the GA to find the solution with the smaller total length for the cables in the network.
![]()
Table 2. Location of the wind generators of the example wind farm.
![]()
Table 3. Data and costs associated to cables/structures.
![]()
Table 4. Objectives of the definition of the example system’s internal grid
4.2. Results Obtained through the Application of the Model for the Cases Analyzed
Among all the viable solutions found for the cases of the example farm studied, the best configuration of each case is represented in Figures 6-10. The costs calculated for these configurations are summarized in Table 5 and represented in the graph of Figure 11.
![]()
Figure 6. Configuration of the best viable solution of the example wind farm’s internal grid for cases 1 and 2.
![]()
Figure 7. Configuration of the best viable solution of the example wind farm’s internal grid for cases 3 and 7.
![]()
Figure 8. Configuration of the best viable solution of the example wind farm’s internal grid for case 4.
![]()
Figure 9. Configuration of the best viable solution of the example wind farm’s internal grid for case 5.
![]()
Figure 10. Configuration of the best viable solution of the example wind farm’s internal grid for cases 6 and 8.
![]()
Figure 11. Costs of the best viable solution for the internal grid for the cases analyzed.
![]()
Table 5. Results for the best viable solution for the internal grid for the cases analyzed.
In the figures, the substation is represented by the square and the wind generators are represented by the circles. The edges in yellow represent the 95 mm2 cable, in magenta the 120 mm2 cable, in cyan the 185 mm2 cable, in red the 240 mm2 cable, in green the 300 mm2 cable, and in blue the 400 mm2 cable.
The best alternatives found for the example wind farm’s internal grid are the Cases 1 and 2, with a total cost of R$ 1,620,076.92. However, these alternatives have not incurred in a smaller cost when the objectives of loss and investment reduction are analyzed separately. The objective function for the Case 1 guides the GA towards the minimum Capex and Opex, and for the optimum cable for the section. In addition, the objective function of the Case 2 considers the Capex and the optimum cable. Therefore, both cases are equivalent since the optimum cable already considers Opex calculation.
Cases 3 and 7 also presented the same costs, which were extremely high due to the high cost of the initial investment. This result was expected since the optimized solution for the internal grid is oriented exclusively towards the minimization of electrical losses, not taking the investment in consideration. It is also noted that the optimum cable does not influence the result. The topology of the internal grid of these cases defines a network connecting each wind generator to the substation, considerably increasing the investment costs for cables, building, and distribution boards.
Similarly, since the optimization of the cable in each section is not being considered, Cases 6 and 8 produce the same results. It happens because the initial investment decreases when the length of the internal grid is smaller.
With the purpose of demonstrating the differences among the best viable alternatives for the cases analyzed, Figure 12 shows a comparison detailing their differences in investment and operational costs. The value of 100% was attributed to the smallest cost, in Table 5; and all the other costs are normalized according to this value.
In Case 4, the objective is to find the smaller distance solution with an optimization of the cable per section. Figure 12 demonstrates that in this Case the total cost is very
![]()
Figure 12. Comparison of best solutions for cases analyzed.
close to the costs in Case 1 and 2. The investment costs are also very close to the costs of Case 1 and 2, and the topology of the grid is only slightly different. Only the operational costs are more significantly different. It also shows that Cases 3 and 7 have the smallest Opex, since the objective of these cases is to find the best network solution for the smallest Opex. Nevertheless, Capex is much higher, thus increasing total cost.
Results obtained in Cases 3 and 7 of this paper (study) show that when objective function is driven just by electric losses throughout plant life cycle the initial investment required is very high, about 4.5 times greater than the objective functions driven by Capex, Opex and optimal cable. It is observed that this investment is not recovered throughout plant life cycle, since total cost is also very high, more than 300%. Therefore, it can be affirmed that taking into consideration just the electric losses objective when designing internal net represent a significant waste of resources.
Similarly, it has been noted that the objective function driven only by Capex and distance, Cases 6 and 7 respectively, also didn’t present good results. Although Capex is 11% lower, Opex increased 73%, resulting in a final cost 11% higher.
The optimal cable methodology has been considered in Cases 1 and 5 and, on the other hand, has been proven to be important for the Wind farm studied since result in 6% of total cost reduction.
5. Conclusions
The influence of the objective function in the solution of the internal grid was proposed and demonstrated in 8 cases studied with different objectives. It can be affirmed that the best solution found for the wind farm studied is the one shown in Case 1. In this Case, the objective function considers the investment and the operational costs and the criterion of the optimum cable for each section of the internal grid. The objective of Case 2 was to find the best solution for the internal grid considering the investment costs, applying the criterion of cable optimization in each section. It reached the same solution of Case 1 for the example wind farm studied.
Objectives that considered exclusively the operational costs for the solution of the wind farm’s internal grid were shown not to be attractive. It happened because the investment cost is extremely high and the topology does not optimize the cables and the construction of the network.
Eight cases with different objectives were analyzed for an example wind farm, leading to some conclusions. Therefore, different objectives are expected to be included in the function in order to orient the GA towards the search for the best solution of the wind farm’s internal grid. Other examples are also expected to be tested.