A Contribution to the DLF-Theory: On Singularities of the SU(2,2)-Action in U(1,1) ()
1. Introduction
The Lie groups U(2) and U(1,1) are the two main objects to be dealt with in this paper. Introduce U(2) as the totality of all two by two matrices Z (complex entries allowed) which satisfy
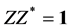 .
.
Here 1 is the unit matrix.
Similarly, U(1,1) is the totality of all two by two matrices U which satisfy
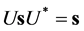 .
.
Here s is the diagonal matrix with entries 1, −1.
Often, these two Lie groups (especially when they carry bi-invariant metric of Lorentzian signature―see [1] ) are denoted D = U(2) and F = U(1,1). Recall that Segal’s chronometric theory (see [2] ) is based on space-time D. The DLF-theory is based on the D, L and F triad. Hence, it can be viewed as a generalization of Segal’s theory (the main tenets of the DLF-theory are given in [1] ).
Recall that the notion of a parallelization (of a space-time bundle―see [2] , Section IV), for the definitions and for existence theorems) is an important mathematical tool in modern theoretical physics, in general, and in the chronometric approach, in particular. It is even more important in the DLF-picture. Let us remind a few quantum- mechanical features, first.
According to quantum mechanics, each object is assigned its state (or wave function but this latter notion we better reserve for a more specialized situation, namely, after a parallelization has been applied). An elementary particle (it “lives” in a certain world W of events) is described by the set of its possible states. The latter set is a certain subspace of the section space (sections can later be specified as smooth, or square-integrable, etc.―this is not the main concern here) of a certain vector bundle over W. At this point, states are not, yet, number-valued (for a scalar particle) or Ck-valued (k > 1, for particles of non-zero spin). One way or the other, we then need to convert to parallelized sections (to wave functions, in other words).
The respective Hilbert space can then be determined. It has become an acknowledged way of modern theoretical physics to describe elementary particles and their interactions in terms of induced representations of the (respective) symmetry group. As it is put in [3] , “the main philosophical point of these developments is perhaps the importance of induced representations, not purely as representations, but as actions on the homogeneous vector bundles that naturally emerge from the induction process. This additional structure provides a spatio-temporal labeling of the vectors in the group representation space that is absolutely essential for the formation of local nonlinear interactions, and relatedly, for causality considerations”.
Conventional quantum mechanics uses representations of the Poincare group, which are induced from its Lorentz subgroup as in Wigner’s seminal work, [4] . The underlying space-time is the Minkowski world M (the one of Special Relativity). There was no formal parallelization involved since it was unthinkable of a better group than M’s vector group (flat parallelization, or M-parallelization, according to the current chronometric terminology). Almost always in literature, physicists merely start with sections having values in a fixed spin space.
In general, the parallelization procedure is essentially defined by choice of the parallelizing (four-dimensional but not necessarily commutative) subgroup N of the group G. Here G is the symmetry group of the space-time W (in our studies, G is the (conformal) group SU(2,2), see below). Typically N is a finite cover of the original space- time W. In Segal’s (with co-authors) publications the mostly used parallelizations were the M-, and the D-ones. Onp.170 of the monograph [5] the role of a parallelization is discussed from the quantum field theory point of view.
In [1] it was suggested to consider other (rather than D and M) parallelizing groups. Here is an important finding of [6] . It is formulated in terms of the commutative D-F diagram: despite of the singularities, both the F-parallelization and its (canonical) comparison to the D-parallelization are possible. Тhe comparison of parallelizations has been introduced in [2] , Section 4.2, as well as certain examples have been discussed there. The thing is that an action of a subgroup (of one or of another) in G can be realized in a simple or in a complicated way―which depends on the choice of the parallelization.
The Lie groups G, GF are introduced as two equivalent representations of SU(2,2). Namely, G is composed of those 4 by 4 matrices g (with unit determinant), which satisfy
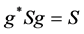 , (1.1)
, (1.1)
where
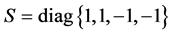 ,
,
a diagonal matrix.
Introduce the 4 by 4 matrix W,
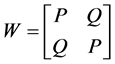 , (1.2)
, (1.2)
which is formed by the 2 by 2 blocks
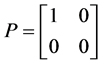 ,
,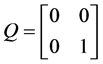 .
.
It is clear that
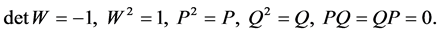 (1.3)
(1.3)
Under the conjugation of the matrix S by W we get
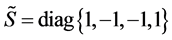 ,
,
which determines another copy (denote it by GF) of SU(2,2). Namely, GF is composed of those 4 by 4 matrices 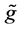 (with unit determinant) which satisfy
(with unit determinant) which satisfy
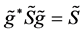 . (1.4)
. (1.4)
The correspondence
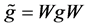 (1.5)
(1.5)
is an isomorphism between Lie groups G, GF.
Each element g of G can be viewed as a 4 by 4 matrix determined via 2 by 2 blocks A, B, C, D:
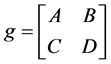 . (1.6)
. (1.6)
Similarly, each element  of GF is composed of the 2 by 2 matrices
of GF is composed of the 2 by 2 matrices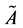 ,
, 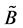 ,
, 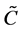 ,
,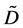 .
.
The linear-fractional action
![]() (1.7)
(1.7)
of G is known ([Se-1976, p.35]) to be defined on the entire D = U(2). The linear- fractional (locally-defined) action
![]() (1.8)
(1.8)
of GF on F = U(1,1) has been introduced in [1] .
Given any two by two matrix M, let W(M) stand for![]() , when this is defined. Define the embedding of F into D by
, when this is defined. Define the embedding of F into D by
![]() , (1.9)
, (1.9)
which is defined for every U in F. The mapping W is conformal but it is not used in this paper. Formula (1.9) is a special case (see [7] ) of the Sviderskiy formula and it is easy to verify that the inverse map
![]() (1.10)
(1.10)
is defined if and only if Z is outside of the torus T where T consists of all matrices K in D = U(2) of the form
![]() (1.11)
(1.11)
with p, q being arbitrary complex numbers of length one.
The following fundamental statement has been proven in [6] :
Theorem 1 (D-F commutative diagram). If ![]() is defined, then
is defined, then
![]() (1.12)
(1.12)
Remark 1. In [6] , it has not been explored when (that is, for which U in F) the right side of (1.12) was defined. Clearly (see (1.8) above), it is defined if and only if the determinant of ![]() is not zero. However, such a condition turns out to be more difficult to verify than the one below (in Theorem 2).
is not zero. However, such a condition turns out to be more difficult to verify than the one below (in Theorem 2).
One of the main goals of the current article is to prove the following
Theorem 2. Let ![]() be in GF and let U be in F. The image
be in GF and let U be in F. The image ![]() is defined if and only if
is defined if and only if ![]() is not on the torus T.
is not on the torus T.
Having in mind certain earlier findings (see [1] [2] [7] ), our Theorems 1, 2, and 3 prove that the new analysis of space-time bundles (based on U(1,1) as the parallelizing group) is mathematically possible. It is of great interest to carry out such an analysis and to compare its conclusions to the ones done on the basis of U(2). Similarly to [2] , Section5, such an analysis should start with considering of scalar bundles. The isometry group K (with the Lie algebra R + su(2) + su(2)) of the world D will be replaced by the isometry group KF (with the Lie algebra R + su(1,1) + su(1,1)) of the world F. When arranging for the basis in the space of the scalar representation, instead of the “left” and the “right” Lie algebras su(2) (see [2] , Section 5.4) the “left” and the “right” Lie algebras su(1.1) are to be chosen. There presentations are over the field of complex numbers. That allows to compare the two “pictures”: the “compact” one―based on U(2), and the “non-compact” one―based on U(1,1).Here one has to bear in mind the famous ‘unitary trick’. Actually, the necessity to consider the F-parallelization is guaranteed by the following fact alone: in an infinite list of all real 4-dimensional Lie algebras only u(2) and u(1,1) turn out to be the reductive ones.
The above indicated problematic is of great interest both for mathematics (covariance of wave equations, invariant forms in spaces of induced representations, classes of special functions, etc.) as well as for physics. Namely, in [8] , pp. 88-89, it is suggested to identify the invariant subspace of the so-called spannor [9] representation with the totality of proton states (which would have explained the proton’s stability).
2. Proof of Theorem 2
Notice that the matrix g(Z) is on the torus T if and only if
![]() , (2.1)
, (2.1)
where a matrix K is of the form (1.11).
For any of the 2 by 2 matrices involved, denote their corresponding entries as follows:
![]() ,
, ![]() etc. (2.2)
etc. (2.2)
Then the above (2.1) reads as the equality
![]() (2.3)
(2.3)
of these two matrices with entries
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
In accordance with (2.2), the entries of L in (2.3) are L1, L2, L3, L4; they are expressed in terms of the entries of matrices A, Z, B in accordance with (2.2) and with the left side of (2.1). The entries of N in (2.3) are N1, N2, N3, N4; they are expressed in terms of the entries of matrices K, C, Z, and D in accordance with the right side of (2.1).
In what follows, it is assumed that (1.5) and (1.9) from Section 1 hold. To adequately understand the ongoing notation, the reader is referred to (1.8) from above. Let us start with
Lemma. ![]() is singular if and only if
is singular if and only if ![]() is singular. Either singularity takes place if and only if (2.3) holds―that is, if
is singular. Either singularity takes place if and only if (2.3) holds―that is, if ![]() is on the torus T.
is on the torus T.
Proof. Let ![]() be singular. This is equivalent to the singularity of the matrix
be singular. This is equivalent to the singularity of the matrix
![]() , (2.4)
, (2.4)
where![]() . The matrix V has the following entries:
. The matrix V has the following entries:
![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
The singularity of V (expressed as proportionality of its rows) is equivalent to the existence of a certain (not necessarily real) number q to satisfy the equality of the second rows in (2.3):
![]() , and
, and ![]()
![]() .
.
In other words, the matrix g(Z) is as follows:
![]() (2.5)
(2.5)
Since the matrix (2.5) has to be an element of U(2), v = 0 holds. It means that ![]() is on the torus T and that (2.1) and (2.3) hold. Now, the equality of the first rows in (2.3) is equivalent to the singularity of the matrix
is on the torus T and that (2.1) and (2.3) hold. Now, the equality of the first rows in (2.3) is equivalent to the singularity of the matrix
![]() . (2.6)
. (2.6)
This last matrix has entries
![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Similarly, the singularity of the matrix (2.6) is equivalent to the existence of a certain (not necessarily real) number p to satisfy the equality of the first rows in (2.3). Again, g(Z) has to be on the torus T, and the entire (2.3) has to hold. Equality of the second rows in (2.3) forces the matrix ![]() to be singular. Lemma is proven.
to be singular. Lemma is proven.
Let us now proceed with
Theorem 2. Let ![]() be in GF and let U be in F. The image
be in GF and let U be in F. The image ![]() is defined if and only if
is defined if and only if ![]() is not on the torus T.
is not on the torus T.
Proof. Let ![]() exists. Then according to [6] , Theorem 1,
exists. Then according to [6] , Theorem 1,
![]() . (2.7)
. (2.7)
This implies ![]() being off the torus T, since (as it has been mentioned in Section 1) W is one-to-one between F and D\T.
being off the torus T, since (as it has been mentioned in Section 1) W is one-to-one between F and D\T.
If ![]() is not on the torus T, then according to Lemma,
is not on the torus T, then according to Lemma, ![]() is non- singular (which means that
is non- singular (which means that ![]() is defined). Theorem 2 is proven.
is defined). Theorem 2 is proven.
Remark 2. Several examples of transformations ![]() are presented below. It turns out that the “
are presented below. It turns out that the “![]() is on/off the torus T” condition is easier to verify than to determine whether the
is on/off the torus T” condition is easier to verify than to determine whether the ![]() is zero or not.
is zero or not.
3. Explicit Description of Singularities of a Transformation ![]()
For a given![]() , let us denote by
, let us denote by ![]() the totality of all matrices U in F = U(1,1) where
the totality of all matrices U in F = U(1,1) where ![]() is undefined. Let g,
is undefined. Let g, ![]() satisfy (1.5).
satisfy (1.5).
If a matrix K is the image of Z under g, then the equality
![]() (3.1)
(3.1)
holds. Clearly, (3.1) is equivalent to
![]() . (3.2)
. (3.2)
Additionally, let a matrix K be of the form (1.11). Since g is a bijection of D, the matrix ![]() is non-degenerate. Hence
is non-degenerate. Hence
![]() . (3.3)
. (3.3)
For a matrix U in![]() , the matrix
, the matrix ![]() is of the form (1.11). Hence, the set of all matrices Z (which satisfy (3.3)) is defined by the ranges of parameters p, q in (1.11). Now, exclude those matrices Z which have zeros as (both) entries on the main diagonal and denote the remaining set by Y. In other words, exclude those matrices Z which belong to the torus T. We have thus proven the following
is of the form (1.11). Hence, the set of all matrices Z (which satisfy (3.3)) is defined by the ranges of parameters p, q in (1.11). Now, exclude those matrices Z which have zeros as (both) entries on the main diagonal and denote the remaining set by Y. In other words, exclude those matrices Z which belong to the torus T. We have thus proven the following
Theorem 3. (Description of singularities of![]() ).The set
).The set ![]() is the image of the above set Y under the map (1.10):
is the image of the above set Y under the map (1.10):
![]() . (3.4)
. (3.4)
Let us continue to discuss (including examples―see below) the set (3.4) properties (in other words, to discuss a domain of a transformation![]() ). On the basis of (3.4), the next statement holds true.
). On the basis of (3.4), the next statement holds true.
Corollary 1. ![]() is diffeomorphic to a subset of a (two-dimensional) torus.
is diffeomorphic to a subset of a (two-dimensional) torus.
As the first example, consider the following one-parameter subgroup in G: each g is determined by blocks
![]() . (3.5)
. (3.5)
Here c = ch(t/2), s = sh(t/2)―hyperbolic cosine and sine of a real parameter t. Assume that t is not zero (that is, g is not an identical map). Interestingly, the matrix ![]() is the same asg. It is an important example (see [2] , p. 85) since the isometry sub-algebra and the infinitesimal generator of the subgroup (3.5) generate the entire (15-dimensional) Lie algebra su(2,2). This holds both for the D-case, as well as for the F-case. Recall that each of the isometry groups is determined by the totality of all block-diagonal matrices: (1.6) for D, and its analogue for F. In [1] , Theorem 9, it was proven that these isometries of F act without singularities on it.
is the same asg. It is an important example (see [2] , p. 85) since the isometry sub-algebra and the infinitesimal generator of the subgroup (3.5) generate the entire (15-dimensional) Lie algebra su(2,2). This holds both for the D-case, as well as for the F-case. Recall that each of the isometry groups is determined by the totality of all block-diagonal matrices: (1.6) for D, and its analogue for F. In [1] , Theorem 9, it was proven that these isometries of F act without singularities on it.
Proposition 1. Each matrix Z in (3.3) is of the form
![]() (3.6)
(3.6)
The proof reduces to a (3.5)-based direct computation. Notice that for any (admissible in these circumstances) choice of parameters p, q, t, the expression (![]() ) in (3.6) is never zero.
) in (3.6) is never zero.
Hence, the following statement holds.
Corollary 2. The set of all singular points of a transformation (3.5) is W-diffeomor- phic to a set which is a (two-dimensional) torus with acircle cut off it: this circle is determined by the equation pq = 1 in (3.6).
Recall [1] , Section 6, where it has been shown that transformations (3.5) are singular in F. The example from there corresponds to a choice pq = −1 in (3.6).
Corollary 3. ![]() is contained in the subgroup SU(1,1) of the group F = U(1,1).
is contained in the subgroup SU(1,1) of the group F = U(1,1).
Proof. Applying Theorem 3, compute W(Z), where Z is an element of the set Y. One gets W(Z) as the product RS where
![]() (3.7)
(3.7)
![]() ,
, ![]() ,
,![]() . From (3.7) it follows that the determinant of the matrix W(Z) equals 1. Corollary 3 is thus proven.
. From (3.7) it follows that the determinant of the matrix W(Z) equals 1. Corollary 3 is thus proven.
As the second example, consider a two-parameter group А in G which is an (Abelian) subgroupА from the Iwasawa decomposition G = КAN. An arbitrary element min А is of the form
![]() (3.8)
(3.8)
where the blocks (1.6) of the matrix g are as follows:
![]() ,
, ![]() ,
, ![]() ,
,![]() . (3.9)
. (3.9)
Here c = cht1, s = sht1, hyperbolic cosine and sine of a real parameter t1. The blocks (1.6) of the matrix f are as follows:
![]() ,
, ![]() ,
, ![]() ,
,![]() . (3.10)
. (3.10)
Here c = cht2, s = sht2, hyperbolic cosine and sine of a real parameter t2.
The following statement can be proven by a direct computation:
Proposition 2. For an arbitrary element m of the form (3.8), the matrix Z in (3.3) belongs to the torus T, given by (1.11). Namely,
![]() (3.11)
(3.11)
where c1 = cht1, s1 = sht1, с2 = cht2, s2 = sht2. Notice that none of the denominators in (3.11) vanishes since![]() .
.
In other words, restriction onto T of a transformation (3.8) is a bijection of T. The mapping W is inapplicable to matrices (3.11).That is why (according to Theorem 3) the set ![]() is an empty one. We have thus proven
is an empty one. We have thus proven
Corollary 4. Each transformation ![]() is everywhere defined on U(1,1).
is everywhere defined on U(1,1).
Remark 3. Corollary 4 can be proven on the basis of Theorem 2: in this case each transformation m of the form (3.8) is a bijection of the set D\T onto itself. In other words, none of the matrices ![]() is an element of the torus T.
is an element of the torus T.
Remark 4. Corollary 4 is coherent to the matrix ![]() being a block-diagonal one (compare to [1] , Theorem 9).
being a block-diagonal one (compare to [1] , Theorem 9).
4. Conclusion
The action (1.8) of GF on F = U(1,1) has been introduced in [1] where it has been detected that this action has singularities. In [6] the fundamental relationship (1.12) between the action of G on D = U(2) and of GF on F has been determined. However, in [6] , it has not been explored when (that is, for which U in F) the right side of (1.12) was defined. Our Theorem 2 provides these singularities’ general (“geometric”) description. Theorem 3 and examples (in Section 3) indicate that the description is quite a working one. In particular, it is now guaranteed that the new analysis of space-time bundles (based on U(1,1) as the parallelizing group) is mathematically possible.