1. Introduction
Let F be a skew field and  be the set of all matrices over F. For
be the set of all matrices over F. For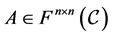 , the matrix
, the matrix  is said to be the group inverse of A, if
is said to be the group inverse of A, if
 .
.
and is denoted by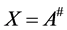 , and is unique by [1] .
, and is unique by [1] .
In [12] the existence of anti-reflexive with respect to the generalized reflection anti- symmetric matrix 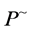 and solution of the matrix equation
and solution of the matrix equation 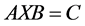 in Minkowski space
in Minkowski space 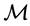 is given. In [13] necessary and sufficient condition for the existence of Re-nnd solution has been established of the matrix equation
is given. In [13] necessary and sufficient condition for the existence of Re-nnd solution has been established of the matrix equation  where
where  and
and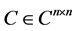 . In [14] partitioned matrix
. In [14] partitioned matrix 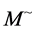 in Minkowski space
in Minkowski space  was
was
taken of the form 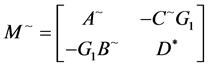 to yield a formula for the inverse of
to yield a formula for the inverse of 
in terms of the Schur complement of![]() .
.
In this paper ![]() and
and ![]() denote the conjugate transpose and Minkowski adjoint of a matrix P respectively.
denote the conjugate transpose and Minkowski adjoint of a matrix P respectively. ![]() denotes the identity matrix of order
denotes the identity matrix of order![]() . Minkowski Space
. Minkowski Space ![]() is an indefinite inner product space in which the metric matrix associated with the indefinite inner product is denoted by G and is defined as
is an indefinite inner product space in which the metric matrix associated with the indefinite inner product is denoted by G and is defined as
![]() satisfying
satisfying ![]() and
and![]() .
.
G is called the Minkowski metric matrix. In case![]() , indexed as
, indexed as![]() , G is called the Minkowski metric tensor and is defined as
, G is called the Minkowski metric tensor and is defined as ![]() [12] . For any
[12] . For any![]() , the Minkowski adjoint of P denoted by
, the Minkowski adjoint of P denoted by ![]() is defined as
is defined as ![]() where
where ![]() is the usual Hermitian adjoint and G the Minkowski metric matrix of order n. We establish the necessary and sufficient condition for the existence
is the usual Hermitian adjoint and G the Minkowski metric matrix of order n. We establish the necessary and sufficient condition for the existence
and the representation of the group inverse of a block matrix ![]() or
or ![]()
in Minkowski space, where![]() . We also give a sufficient condition for
. We also give a sufficient condition for ![]() to be similar to
to be similar to![]() .
.
2. Lemmas
Lemma 1. Let![]() . If
. If
![]() ,
,
then there are unitary matrices ![]() such that
such that
![]()
where ![]() and
and![]() .
.
Proof. Since ![]() there are two unitary matrices
there are two unitary matrices ![]() such that
such that
![]()
where
![]() .
.
Now
![]()
and
![]()
From ![]() we have
we have
![]()
and from ![]() we get
we get
![]()
So,
![]()
Lemma 2. Let
![]() .
.
Then the group inverse of M exists in ![]() if and only if the group inverse of
if and only if the group inverse of ![]()
exists in ![]() and
and![]() . If the group inverse of
. If the group inverse of ![]() exists in M,
exists in M,
then
![]()
Proof. Since![]() , suppose group inverse of
, suppose group inverse of ![]() exists in
exists in ![]() and
and![]() . Now
. Now
![]() .
.
But ![]() because
because ![]() exists
exists![]() . There-
. There-
fore ![]() exists in
exists in![]() .
.
Conversely, suppose the group inverse of M exists in![]() , then it satisfies the following conditions: 1)
, then it satisfies the following conditions: 1) ![]() 2)
2) ![]() and 3)
and 3)![]() . Also
. Also
![]() .
.
Let ![]() then,
then,
1)
![]()
2)
![]()
3)
![]()
Lemma 3. Let![]() , and
, and![]() . Then the
. Then the
group inverse of M exists in ![]() if and only if the group inverse of
if and only if the group inverse of ![]() exists in
exists in ![]() and
and![]() . If the group inverse of M exists in
. If the group inverse of M exists in![]() , then,
, then,
![]()
Proof. The proof is same as Lemma 2.
Lemma 4. Let![]() . If
. If
![]()
then the following conclusions hold:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Proof. Suppose![]() , then by Lemma 1 we have
, then by Lemma 1 we have
![]()
where![]() . Then
. Then
![]()
Since ![]() we have that
we have that ![]() is invertible. By using Lemma 2 and 3 we get
is invertible. By using Lemma 2 and 3 we get
![]()
Then, 1)
![]()
Similarly we can prove 2) - 5).
3. Main Results
Theorem 1. Let ![]() where
where![]() , then
, then
1) The group inverse of M exists in ![]() if and only if
if and only if
![]() .
.
2) If the group inverse of M exists in![]() , then
, then![]() , where
, where
![]()
Proof. 1) Given![]() . Suppose
. Suppose ![]() then,
then,
![]() . We know that
. We know that
![]() so,
so,![]() .
.
Therefore the group inverse of M exists. Now we show that the condition is ne- cessary,
![]()
![]() .
.
Since the group inverse of M exists in ![]() if and only if
if and only if![]() , we have
, we have
![]()
Also
![]()
Then ![]() and
and![]() . Therefore,
. Therefore,
![]() .
.
From
![]()
and
![]() ,
,
we have
![]()
Since
![]()
and
![]() ,
,
we get
![]() .
.
Thus
![]() .
.
Then there exists a matrix ![]() such that
such that![]() . Then
. Then
![]() .
.
So, we get
![]() .
.
2) Let![]() , we will prove that the matrix X satisfies the conditions of
, we will prove that the matrix X satisfies the conditions of
the group inverse in![]() . Firstly we compute
. Firstly we compute
![]()
![]()
Applying Lemma 4 1), 2) and 5) we have
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now
![]()
![]()
![]()
![]()
![]() □
□
Theorem 2. Let ![]() in
in![]() , where
, where![]() ,
,
![]()
Then,
1) the group inverse of M exists in ![]() if and only if
if and only if
![]() .
.
2) if the group inverse of M exists in![]() , then
, then![]() , where
, where
![]()
Proof. 1) Given![]() . Suppose
. Suppose ![]() then,
then,
![]() .
.
We know that
![]()
so,
![]() .
.
Therefore the group inverse of M exists in![]() . Now we show that the condition is necessary,
. Now we show that the condition is necessary,
![]()
![]()
![]()
Since the group inverse of M exists in ![]() if and only if
if and only if![]() . We know
. We know
![]()
Also
![]()
Then ![]() and
and ![]() Therefore
Therefore
![]()
From
![]()
and
![]()
we have
![]()
Since
![]()
and
![]() ,
,
we get
![]() .
.
Thus
![]()
Then there exist a matrix ![]() such that
such that ![]() Thus
Thus
![]()
So, we get![]() .
.
2) Proof is same as Theorem 1 2).
Theorem 3. Let ![]() if
if
![]() .
.
Then ![]() and
and ![]() are similar.
are similar.
Proof. Suppose![]() , then by using Lemma 1, there are unitary matrices
, then by using Lemma 1, there are unitary matrices ![]() such that
such that
![]() ,
, ![]()
where![]() . Hence
. Hence
![]()
![]()
So ![]() and
and ![]() are similar.
are similar.