Linear and Nonlinear Electron Beam Heating of Magnetized, Motional, and Dusty Plasma ()
1. Introduction
Electron beam-plasma interaction presents a great interest for many applications in areas like development of new methods in amplification and generation of electromagnetic waves, acceleration of charged particles in plasma (Plasma Accelerator). Besides, the electron beam-plasma system showed great importance via plasma generation, design of microwave tubes waveguides, explanation of natural phenomena that occur in space and solar plasmas, material studies, compact torus formation, generation of x-ray and microwave, and others.
Multiple harmonic generation by laser/beam-plasma interaction has been widely investigated [9] - [13] . The generation of harmonics through a nonlinear mechanism driven by bunching at the fundamental has sparked interest as a path toward enhancing and extending the usefulness of an x-ray free-electron laser (FEL) facility. Besides, the sensitivity of nonlinear harmonic generation to electron beam quality is found to play a crucial role via FEL [14] [15] .
Currently, high-order harmonic generation (HHG) is considered as one of the more efficient technique for producing coherent short-wavelength radiation in a broad spectral range [16] . Also, the nonlinear cold plasma-bunched beam interaction represents an interesting application for plasma wakefield accelerator [17] .
From the point of view of beam-plasma interaction, the impact of dust on plasma is an important explosed field of research. It is increasingly being studied these days due to their applications in a wide range of fields. The presence of relatively highly charged and massive dust grains in a plasma can modify or influence the collective phenomena of the plasma. The possible dust modes may explain the extremely low-frequency fluctuations, new channels for the parametric coupling of other waves, generation of wakefields, etc., in dusty plasma. The impurities coming off from the walls of fusion device can create a dusty plasma at the edge of the discharge. These particles can enhance power loss due to radiation and dilution of fuel as well as can cool down the hot ion by charge-exchange process [18] - [23] .
The subject of this paper is to study and investigate the electron beam heating of magneto-active motional dusty plasma under discuss different effects or parameters.
Section 2 explores the interaction of electron beam with a homogeneous magnetized non-motional plasma and plasma heating. Section 3 studies linear, non-motional (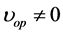 ) and clean plasma in static magnetic field, while Section 4 is devoted to study the effects of the dust on the nonlinear beam interaction with non-motional plasma. Dusty plasma is characterized as a low-temperature ionized gas whose constituents are electrons, ions, and micron-sized dust particulates. The latter is usually negatively charged due to the attachment of the background plasma electrons on the surface of dust grains via collisions. The physical processes in dusty plasmas are interesting because of their importance for a number of applications in space plasmas and the earth s environment, as well as in the laboratory, and in several technologies. The dust grains have a strong effect on energy absorbed in the plasma. In Section 5, we study and investigates the effects of motional plasma (
) and clean plasma in static magnetic field, while Section 4 is devoted to study the effects of the dust on the nonlinear beam interaction with non-motional plasma. Dusty plasma is characterized as a low-temperature ionized gas whose constituents are electrons, ions, and micron-sized dust particulates. The latter is usually negatively charged due to the attachment of the background plasma electrons on the surface of dust grains via collisions. The physical processes in dusty plasmas are interesting because of their importance for a number of applications in space plasmas and the earth s environment, as well as in the laboratory, and in several technologies. The dust grains have a strong effect on energy absorbed in the plasma. In Section 5, we study and investigates the effects of motional plasma (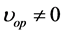 ) on the heating processes due to beam-plasma interaction. Finally, in Section 6, we investigate the effects due to the inhomogeneity of beam velocity on both power absorption and generated electric field.
) on the heating processes due to beam-plasma interaction. Finally, in Section 6, we investigate the effects due to the inhomogeneity of beam velocity on both power absorption and generated electric field.
The electron beam is considered to be injected into plasma under the effect of static magnetic field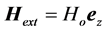 . We use the well known expression for the amount of energy absorbed by the plasma per unit time S as:
. We use the well known expression for the amount of energy absorbed by the plasma per unit time S as:
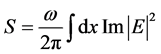 (1)
(1)
where E is the electric field generated in the system.
2. Linear, Non-Motional and Clean Plasma in Static Magnetic Field
The equations of motion, and the continuity equation for electron beam, which travels along the magnetic field are:
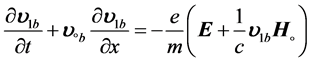 (2)
(2)
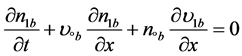 (3)
(3)
while the equation of motion, and the continuity equation for cold inhomogeneous plasma electrons in the static magnetic field are given by:
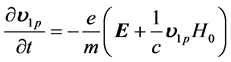 (4)
(4)
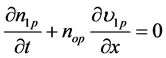 (5)
(5)
where, 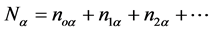 ,
, 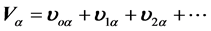 and
and .
.
For non motional plasma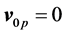 .
. 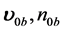 and
and 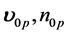 are the unperturbed velocity and density of the beam and plasma respectively.
are the unperturbed velocity and density of the beam and plasma respectively.
Solving the above system of equations we can derive the following expressions for the perturbed densities:
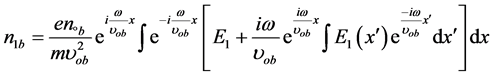 (6)
(6)
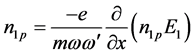 (7)
(7)
where, ![]() , and
, and ![]() is the cyclotron frequency.
is the cyclotron frequency.
Using relations (6) and (7) in Poisson’s equation
![]() (8)
(8)
we obtain the following wave equation for the electric field:
![]() (9)
(9)
where, ![]()
Introducing the electric field form:![]() , Equation (9) reduces to:
, Equation (9) reduces to:
![]() , where,
, where,![]() (10)
(10)
Then we can write the final solution of (9) in the simple form:
![]() (11)
(11)
Set (11) into (1), the energy absorbed absorbed by the beam reads:
![]() (12)
(12)
Relation (12) is investigated for different cases of magnetic field: zero, weak and strong magnetic fields.
3. Linear Dusty Plasma Heating
For dusty plasma, we use the system of Equations (2)-(5) with![]() , then we obtain the following equation of motion, and the continuity equation as:
, then we obtain the following equation of motion, and the continuity equation as:
![]() (13)
(13)
![]() (14)
(14)
Solving the above system of equations we can derive the following expressions for the dust perturbed density:
![]() (15)
(15)
where, ![]() Charge of dust.
Charge of dust.
Using relations (7) and (8), (15) in Poisson’s equation:
![]() (16)
(16)
we obtain the following wave equation for the perturbed electric field:
![]() (17)
(17)
where, ![]() ,
,![]() .
.
The energy absorbed in this case reads:
![]() ,
,![]() (18)
(18)
In linear regime, if ![]() and
and ![]() are the energy absorbed by the beam in clean and in dusty plasma, respectively, then:
are the energy absorbed by the beam in clean and in dusty plasma, respectively, then:
![]()
It is clear that, existence of dust leads to less energy absorption by the plasma.
The generated electric field under the effect of dusty and clean plasma is shown in Figure 3.
4. Nonlinear Dusty Plasma Heating
In nonlinear regime, the equation of motion, and the continuity equation for electron beam, which travels along the magnetic field are:
![]() (19)
(19)
![]() (20)
(20)
The equation of motion, and the continuity equation for homogeneous plasma electrons in a static magnetic field perpendicular to the plasma are given by:
![]() (21)
(21)
![]() (22)
(22)
The dusty nonlinear equations of motion, and continuity are:
![]() (23)
(23)
![]() (24)
(24)
Solving the above system of equations we can derive the following expressions for the nonlinear perturbed densities:
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
where, ![]() (second harmonic generation), and
(second harmonic generation), and
![]()
![]()
![]()
Using relations (25)-(27), and considering the nonlinear form of Poisson’s Equation (16), we obtain the following wave equation for the nonlinear generated electric field:
![]() (28)
(28)
where, ![]() ,
,![]() .
.
Accordingly, we obtain the energy absorption from the beam as:
![]() ,
,![]() (29)
(29)
From (18) and (29) we conclude that:
![]() (30)
(30)
Ratio (30) shows that, for nonlinear interaction the existence of dust leads to less energy absorption by the plasma as in the linear regime.
Figure 4 shows the generated electric field under the effect of dusty and clean nonlinear plasma. In this regime amplification of electric field in dusty plasma is clear compared to clean plasma.
Generally speaking, nonlinearity plays a crucial role in the amplification of the electric field generated due to beam-plasma interaction, for different situations, compared to linear case.
5. Motional Plasma
For motional plasma, for the electron beam, we use the above system of Equations (2), (3 and (6). On the other hand, the equation of motion, and the continuity equation for homogeneous plasma electrons in a static magnetic field perpendicular to the plasma are given by:
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
Accordingly, we obtain the following expressions for the perturbed plasma density
![]() (34)
(34)
Using relations (6) and (34) in Poisson’s Equation (8), we obtain the following wave equation for the electric field in motional plasma
![]() (35)
(35)
where,
![]() ,
, ![]() ,
,
In this case the energy absorbed is:
![]() (36)
(36)
From this relation and non-motional relation (12) we conclude that:
![]() (37)
(37)
Ratio (37) shows that, the existence of plasma motion leads to less energy absorption from the beam, as indicated in Figure 6.
Figure 7 shows the reduction of the generated electric field under the effect of motional plasma compared to non-motional plasma.
6. Inhomogeneity of Beam Velocity Effects
Let us consider the case of an electron beam moves with inhomogeneous velocity, i.e.,![]() . In this case we have to include the term
. In this case we have to include the term ![]() in both the equations of
in both the equations of
motion (2) and continuity. Accordingly, we obtain the perturbed beam velocity and density as:
![]() (38)
(38)
![]() (39)
(39)
where, ![]() , and the equation controlling the perturbed electric field is given by:
, and the equation controlling the perturbed electric field is given by:
![]() ,
,![]() (40)
(40)
Using mathematical tools used in previous sections, we obtain, ![]() , hence the energy absorbed in this case:
, hence the energy absorbed in this case:
![]() (41)
(41)
Figure 8 shows that the sharp increase in the generated electric field due to![]() ―after a critical distance in the plasma―compared to the case
―after a critical distance in the plasma―compared to the case![]() . This positively affects the plasma heating, and creates a type of plasma acceleration.
. This positively affects the plasma heating, and creates a type of plasma acceleration.
7. Conclusions and Final Remarks
The Electron Beam Heating of Magneto-Active Motional Dusty Plasma is investigated.
Generally speaking, nonlinear process, dust, plasma motion, and beam velocity inhomogeneity, are found to play a crucial role via power absorbed by the beam and the generated electric field in the system.
It is shown that strong magnetic field generates an intense electric field compared to zero, and weak magnetic fields (Figure 1). In turn, an applied external static magnetic field leads to enhanced power absorption from the electron beam, and accordingly to plasma heating in beam-plasma system.
The energy absorbed from the beam in clean (S) and dusty (Sd) plasma (Figure 2), shows that dust causes a loss in the power energy absorbed in the plasma.
Considering nonlinear interaction, ratio (30) shows that dust leads to less energy absorption by the plasma as in the linear regime.
Figure 3 and Figure 4, shows the generated electric field under the effect of dusty and non-dusty plasmas in linear and nonlinear stages. In this regime amplification of electric field in dusty plasma is less compared to clean plasma. However, in clean plasms, the nonlinear effects associated with the generation of second harmonics, plays an important role in the process of energy transfer from the beam to the plasma as
![]()
Figure 1. Generated electric field under the effect of zero, weak and strong magnetic fields.
![]()
Figure 2. Energy absorbed from the beam in clean (S) and dusty (Sd) plasmas.
![]()
Figure 3. Generated electric field under the effect of dusty and clean linear plasma.
![]()
Figure 4. Generated electric field under the effect of dusty and clean nonlinear plasma.
compared with linear stage. This is due to the fact that the electric field intensity at double harmonics is stronger than that of the basic frequency (Figure 5 shows electric field amplification in nonlinear regime).
As application, the generation of second harmonics through a nonlinear mechanism driven by bunching at the fundamental has sparked interest as a path toward enhancing and extending the usefulness of an x-ray free-electron laser (FEL) facility [14] . Currently, high-order harmonic generation (HHG) is considered as one of the more efficient technique for producing coherent short-wavelength radiation in a broad spectral range [16] [24] [25] .
In the motional plasma, the interaction between the electron beam and plasma will occur and induce electrons to exchange energy with plasma waves. The self-magnetic field of the motional electrons is a key parameter of this interaction.
Ratio (37) shows that, the existence of plasma motion leads to less energy absorption of the beam, as indicated in Figure 6. The reduction of the generated electric field under the effect of motional plasma compared to non-motional plasma, is shown in Figure 7.
An interesting result is shown in Figure 8, the sharp increase in the generated electric field due to beam velocity inhomogeneity![]() ―after a critical distance in the plasm compared to the case
―after a critical distance in the plasm compared to the case![]() . This enhanced power absorption of the electron
. This enhanced power absorption of the electron
![]()
Figure 5. Electric field amplification in the nonlinear regime.
![]()
Figure 6. Energy absorbed from the beam in non-motional (S) and motional (Smot.) plasmas.
![]()
Figure 7. Generated electric field under the effect of motional and nonmotional plasma.
![]()
Figure 8. Generated electric field under the effect of inhomogeneous and homogeneous beam velocity.
beam, and positively affects the plasma heating, and may create a type of plasma acceleration.
In due course, we are going to investigate the effects of an inhomogeneous relativistic electron beam (REB) interaction with dusty, motional inhomogeneous plasma placed in an oscillating magnetic field.