Evaluation of the Minimum Size of a Window for Harmonics Signals ()
1. Introduction
One of the most important tools in signal processing is the Nyquist theorem. Many of the processing tools are meaningless if the theorem is not satisfied. To date, the Nyquist theorem is often used in such a way that the acquisition of a signal is made with an excessive sampling frequency.
Sometimes, an overly large amount of samples is chosen. One of the most used tools to remedy the effect of oversampling is the use of windows that reduce noise and spectral leakage. Windows are used in non-parametric estimators and even in spectrograms. In 1978 Fredric J. Harris published his article “On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform” [1] . In this paper a comprehensive study of the properties and characteristics of the different types of windows in the time and frequency domains is conducted. The spectra of the windows are studied in detail, and an exhaustive analysis of the width of lateral and central lobes of a variety of windows is conducted. This analysis shows the effects or consequences of the lobes produced by the spectra of the windows. An example developed by Harris shows the hiding of information from a signal due to the lobes, and invites to select the type of window according to its spectral behavior. The results presented by Harris have not been questioned to date, and it is an important reference for many papers, including articles and books.
For over 30 years, research on the characteristics of the windows that appear in the article by Harris has not changed significantly. Many authors present new algorithms that allow for improvements in the lobes, both lateral and central, in the same direction as Harris [2] - [7] .
As a complement to all previous work, the authors of this paper use the frequency resolution
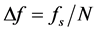 (1)
(1)
to determine the minimum number of samples required in a window.
Due importance has not been given to (1) even though it is fundamental in the analysis as well as in the acquisition of a signal. Without the adequate resolution, the frequency information, important to a particular phenomenon, might be hidden. The evaluation of the frequency resolution, before acquiring a signal or in the process of analyzing it, allows the making of decisions about the use of certain tools, such as the minimum size of a window.
The main contribution of this paper is the possibility of making a precise choice on the number of data that ensures the resolution between two very close frequencies, and diminishes the processing time by reducing the number of data required if the analysis is made before acquisition.
2. The Resolution ∆f
To date, little is known about what the minimum size of a window should be. Usually, the ad-hoc choice depends on the flair and experience of the user.
Harris mentions in his article: “The two operations to which we subject the data are sampling and windowing. These operations can be performed in either order. Sampling is well understood, windowing is less so, and sampled Windows for DFT’s significantly less so!” [1] . In the same article he mentions “Windows are weighting functions applied to data to reduce the spectral leakage associated with finite observation intervals” [1] . Harris makes a detailed analysis of the time and frequency characteristics of the different types of windows. Currently the window type is selected according to its spectrum, but little is known of the minimum size of the window, so it continues to be evaluated subjectively.
Several processing tools like periodograms, spectrograms [8] - [11] , are based on the use of windows. However, the main question of the minimum size of a window remains unanswered.
Examples with experimental and simulated signals, that show the importance of considering , and for which it is possible to evaluate the minimum size of a window are presented.
, and for which it is possible to evaluate the minimum size of a window are presented.
A monochromatic signal with a frequency  is acquired in two different ways. First, the sample rate
is acquired in two different ways. First, the sample rate 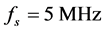 is kept constant and the number of samples N is varied. In the second,
is kept constant and the number of samples N is varied. In the second, 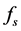 varies and
varies and 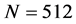 is constant. With these conditions the spectra of Figure 1(a) and Figure 2(a) are obtained.
is constant. With these conditions the spectra of Figure 1(a) and Figure 2(a) are obtained.
In both Figure 1(a) and Figure 2(a), it is possible to notice changes in the amount of spectral leakage. However, the variation of the width of the peaks, which is only noticeable in a zoom-in, can be observed in Figure 1(b) and Figure 2(b). It is interesting to analyze the widest peaks in both figures. In Figure 1(b) the widest peak belongs to the spectral graph with the least number of samples, while the widest peak in Figure 2(b) belongs to the spectral graph with the highest sampling frequency.
![]()
Figure 1. Signal with , constant
, constant 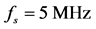 and variable N. (a) The circle shows the variation of the peak amplitudes for each case; (b) Shows the variation of the width of these peaks when zooming-in.
and variable N. (a) The circle shows the variation of the peak amplitudes for each case; (b) Shows the variation of the width of these peaks when zooming-in.
To emphasize the importance of the width of the peaks, a signal was acquired with four frequency components: 1 MHz, 1.01 MHz, 1.05 MHz and 1.1 MHz. The following parameters were used: sampling frequency 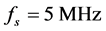 and
and 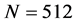 samples. The highest frequency of this signal is 1.1 MHz, thus a sampling frequency of
samples. The highest frequency of this signal is 1.1 MHz, thus a sampling frequency of 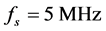 perfectly fulfills the Nyquist theorem. However, the spectrum of the signal is not the one expected, since the original signal had four frequency components, and not only three as may be observed in Figure 3.
perfectly fulfills the Nyquist theorem. However, the spectrum of the signal is not the one expected, since the original signal had four frequency components, and not only three as may be observed in Figure 3.
The resolution in the frequency domain is given by . With
. With 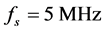
![]()
Figure 2. Signal with , constant N = 512 and variable
, constant N = 512 and variable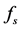 . (a) The circle shows the variation of the peak amplitudes for each case; (b) Shows the variation of the width of these peaks when zooming-in.
. (a) The circle shows the variation of the peak amplitudes for each case; (b) Shows the variation of the width of these peaks when zooming-in.
![]()
Figure 3. Spectrum of a four frequency signal. Perpendicular lines are shown in order to view how with![]() , it is not possible to distinguish one of the components involved in the signal.
, it is not possible to distinguish one of the components involved in the signal.
and![]() , a frequency resolution of
, a frequency resolution of ![]() is obtained. The frequencies which are most closely spaced are 1 MHz and 1.01 MHz. In other words, the separation between them is 10 kHz, and with a frequency resolution of
is obtained. The frequencies which are most closely spaced are 1 MHz and 1.01 MHz. In other words, the separation between them is 10 kHz, and with a frequency resolution of![]() , it is not possible to distinguish the missing component, although the Nyquist theorem requirements have been applied correctly. Besides, there is no information on how many samples are needed; we can see that it is not possible to display the missing component. Sometimes ad-hoc or “subjective” techniques―such as increasing the number of samples or the sampling frequency―are employed until the desired solution is obtained.
, it is not possible to distinguish the missing component, although the Nyquist theorem requirements have been applied correctly. Besides, there is no information on how many samples are needed; we can see that it is not possible to display the missing component. Sometimes ad-hoc or “subjective” techniques―such as increasing the number of samples or the sampling frequency―are employed until the desired solution is obtained.
Even though ![]() is well known, it is not taken into account when the signal is acquired in the time domain, and the Nyquist theorem is applied. It is necessary to use the adequate
is well known, it is not taken into account when the signal is acquired in the time domain, and the Nyquist theorem is applied. It is necessary to use the adequate ![]() and N in the acquisition process, in order to have the desired resolution
and N in the acquisition process, in order to have the desired resolution ![]() in the frequency domain. Figure 4 shows the same experimental composite signal with four frequency components, acquired at two different sampling frequencies with the same number of samples used in Figure 3.
in the frequency domain. Figure 4 shows the same experimental composite signal with four frequency components, acquired at two different sampling frequencies with the same number of samples used in Figure 3.
Figure 4 shows that, for a sampling frequency two and a half times larger than the frequency involved in the signal (a frequency near the Nyquist frequency), it is possible to solve the four frequency components without increasing the number of samples. This result was obtained taking into account ![]() in the acquisition process, which allowed to make a decision in an objective way, by evaluating the convenience of increasing any of the two parameters
in the acquisition process, which allowed to make a decision in an objective way, by evaluating the convenience of increasing any of the two parameters![]() , or N.
, or N.
Based on![]() , it is clear that by increasing
, it is clear that by increasing![]() , while keeping N constant, the outcome would only worsen. It may be inferred that a better frequency resolution is obtained by simply increasing the number of samples. For a signal with
, while keeping N constant, the outcome would only worsen. It may be inferred that a better frequency resolution is obtained by simply increasing the number of samples. For a signal with![]() ,
, ![]() is obtained. This value of
is obtained. This value of ![]() is enough to distinguish the frequency components involved in the signal, Figure 5.
is enough to distinguish the frequency components involved in the signal, Figure 5.
![]()
Figure 5. An increase in the number of samples N = 8192, and not in the sampling frequency 5 MHz, made it possible to distinguish the missing component.
There is a great variety of factors due to which the information in a given signal cannot be clearly observed, such as the noise of the devices used in an experiment, the experiment itself and even the software used to analyze the acquired signal. The instruments with which signals are acquired usually do so at high sampling rates with a small number of samples, regardless of the type of signal. In general, instruments only allow the manipulation of the sampling frequency in within a set of choices provided by the manufacturer. As a result, once the signal is acquired, nothing can be done about the resolution attained. Sometimes, processing techniques are used as remedial tools, but they cannot extract information that does not exist in the acquired signal.
This work focuses on clarifying that the hiding of information in a signal depends, not only on the lobes of the spectra produced by the windows, but also on the fact that the frequency resolution![]() , is an important factor to consider when choosing the size of a window.
, is an important factor to consider when choosing the size of a window.
3. Minimum Size of a Window
To understand the importance of the frequency resolution![]() , we shall retake Figure 4, but this time showing the discrete intervals of
, we shall retake Figure 4, but this time showing the discrete intervals of ![]() in the graphs, Figure 6.
in the graphs, Figure 6.
An important feature to be noted in Figure 6 is the size of ![]() in the different graphs. The dotted graph has smaller
in the different graphs. The dotted graph has smaller ![]() than the one with the solid line. It is clear that large sampling frequencies do not imply small
than the one with the solid line. It is clear that large sampling frequencies do not imply small![]() .
.
In the analysis of different graphs, it was observed that the minimum size of a window was controlled by the size of![]() . In order to distinguish between two closely spaced components, it was necessary that, there is at least one
. In order to distinguish between two closely spaced components, it was necessary that, there is at least one ![]() between them, i.e.:
between them, i.e.:
![]() (2)
(2)
where ![]() are two closely spaced frequency components. With Equation (1) and Equation (2), the minimum number of a window samples, or the minimum size of a window can be determined in terms of
are two closely spaced frequency components. With Equation (1) and Equation (2), the minimum number of a window samples, or the minimum size of a window can be determined in terms of ![]()
![]() (3)
(3)
where ![]() represents the number of samples of the window.
represents the number of samples of the window.
In the example we have ![]() and
and![]() , which implies that
, which implies that
![]() . Applying (3) we get that the minimum size of a window is:
. Applying (3) we get that the minimum size of a window is:
![]() (4)
(4)
![]() (5)
(5)
By applying this result the graphs shown in Figure 7 are obtained. For ![]() less than 1000 samples, it is impossible to observe all the components of the signal under study.
less than 1000 samples, it is impossible to observe all the components of the signal under study.
Inequality (3) allows the objective evaluation of the minimum size of a window.
Equation (2) and Equation (3) provide the minimum size of a window very accurately when components we want to differentiate have very similar amplitudes.
4. Effect of Size vs Type
In this section the effect of the size of a window versus the use of the type of window is analyzed.
Different windows are used on a signal with two frequency components ![]() and
and![]() , both with the same amplitude of one volt,
, both with the same amplitude of one volt, ![]() , and
, and
![]() . The spectrum is shown in Figure 8.
. The spectrum is shown in Figure 8.
![]()
Figure 7. Different window sizes were applied to a four frequency signal with 16,384 samples. For a window of 512 samples, it was not possible to distinguish the four components.
![]()
Figure 8. Spectrum of a signal with two frequency components ![]() and
and![]() , both with the same amplitude of 1 volt.
, both with the same amplitude of 1 volt.
With the above parameters, the minimum size of a window is calculated using Equation (2) and Equation (3),
![]() (6)
(6)
Hence
![]() (7)
(7)
Figure 9 shows the graphs for a window with 64 samples.
As can be seen in Figure 10, an increase on the size of the window provides better resolution and it is therefore possible to better distinguish the signal components involved.
![]()
Figure 9. ![]() in all cases. (a) Rectangular window; (b) Hanning window; (c) Hamming window; (d) Bartlett window; (e) Blackman window; (f) Chebwin window; (g) Triangular window; (h) Henning-Poisson window with α = 0.5. In almost every window it is possible to distinguish the two components, except for the (f) Chebwin and (e) Blackman windows.
in all cases. (a) Rectangular window; (b) Hanning window; (c) Hamming window; (d) Bartlett window; (e) Blackman window; (f) Chebwin window; (g) Triangular window; (h) Henning-Poisson window with α = 0.5. In almost every window it is possible to distinguish the two components, except for the (f) Chebwin and (e) Blackman windows.
![]()
Figure 10. (a) Rectangular window; (b) Hanning window; (c) Hamming window; (d) Bartlett window; (e) Blackman window; (f) Chebwin window; (g) Triangular window; (h) Henning-Poisson window with α = 0.5. In all windows,![]() ; it is possible to distinguish the two components.
; it is possible to distinguish the two components.
In the following example a signal with two components, but with a difference in amplitude of 40 dBs is considered. Three types of windows are used in particular because they tend to hide information [1] . It will be shown that these windows hide information not only because of the lobes provided by their spectrum, but also because of the size of the window.
Figure 11 shows a signal with two frequency components ![]() and
and![]() ,
,
with amplitudes of 1 and 0.01 volts respectively, ![]() and
and![]() .
.
Figure 12 shows the graphs obtained by applying rectangular, Hanning-Poisson and Poisson windows with![]() . It is possible to notice the slightly smaller amplitude component in the different graphs. Previous knowledge of the signal is important in order to determine that the deformation in the figures corresponds to the expected frequencies.
. It is possible to notice the slightly smaller amplitude component in the different graphs. Previous knowledge of the signal is important in order to determine that the deformation in the figures corresponds to the expected frequencies.
With the same sampling parameters, but slightly changing one of the frequencies (as
in [1] );![]() , Figure 13, is obtained.
, Figure 13, is obtained.
![]()
Figure 12. Windows with ![]() applied to the signal of Figure 11. The arrows indicate the location of
applied to the signal of Figure 11. The arrows indicate the location of![]() , which is scarcely visible.
, which is scarcely visible.
However, an increase in the size of the window allows us to see the component with the smaller amplitude; Figure 14.
So far it has been observed that with a frequency resolution of
![]() , two adjacent components can be resolved―re- gardless of the type of window―by increasing the number of samples in the window
, two adjacent components can be resolved―re- gardless of the type of window―by increasing the number of samples in the window![]() , Figure 14.
, Figure 14.
The importance of relative amplitudes of the components can be further analyzed. Analogous to Harris, three windows, rectangular, Poisson and Hanning-Poisson will be
![]()
Figure 13.![]() . The arrows indicate where the smallest amplitude component
. The arrows indicate where the smallest amplitude component ![]() should appear. For this type of windows it is not possible to distinguish the component of smaller amplitude [1] .
should appear. For this type of windows it is not possible to distinguish the component of smaller amplitude [1] .
![]()
Figure 14.![]() , with this size window, it is possible to resolve between two nearby components with a difference in amplitudes of 40 dBs.
, with this size window, it is possible to resolve between two nearby components with a difference in amplitudes of 40 dBs.
applied to a signal with two frequency components, ![]() and
and![]() ;
;
![]() and
and![]() . Three cases will be considered: 1) with a difference in
. Three cases will be considered: 1) with a difference in
amplitudes of 0 dBs, 2) with a difference in amplitudes of 20 dBs, and 3) with a difference in amplitudes of 40 dBs. The results are shown in Figures 15-17.
Figures 15-17 show that the spectral behavior of the windows has little influence on the observation of the frequency components, whether closely spaced components or with a large difference of amplitude.
![]()
Figure 15. Rectangular window applied to a signal with two frequency components. The amplitude difference between the components determines whether the lobes, central or lateral, of a window affects the observation of the component of smaller amplitude.
![]()
Figure 16. Poisson window applied to a signal with two frequency components. The amplitude difference between components determines whether the lobes, central or lateral of a window, affect the observation of the component of smaller amplitude.
5. Applications
The results shown so far allow for a more objective use of nonparametric periodograms. These are processing tools used to reduce significantly the signal leakage by applying spectral windowing, [9] - [12] . Using Equation (2) and Equation (3), Welch’s parametric periodogram was applied to the compound signal with four frequency components that is analyzed in Figure 4 and Figure 5. Figure 18 shows the results.
The Welch parametric periodogram was applied to the same signal considered in Figure 18. Figure 19 shows the periodogram using rectangular windows with 512 samples. Equation (2) and Equation (3) yield Figure 20, which shows a Welch periodogram
![]()
Figure 17. Hanning-Poisson window applied to a signal with two frequency components. The amplitude difference between the components determines whether the lobes, central or lateral, of a window affect the observation of the component of smaller amplitude.
![]()
Figure 18. FFT of a four component signal. N = 16,834 and![]() ;
;![]() .
.
![]()
Figure 19. Welch’s periodogram with rectangular windows of 512 samples.
![]()
Figure 20. Welch’s periodogram with rectangular windows of 1024 samples.
with rectangular windows of 1024 samples.
The decrease in spectral leakage is remarkable in the previous figures, just as the theory predicts. It is clear that, the lower the number of samples in the spectral window used, the more the leakage decreases. However, by choosing a window with few samples, wrong results could be obtained, as can be seen in Figure 19. Assessing the minimum size of a window by using Equation (2) and Equation (3), gives us a greater assurance that the results obtained will be correct. The closely spaced component may be vaguely apparent in Figure 20. It was not possible to observe this component with a window size with less than 1000 samples.
It is clear that increasing the number of samples in the window will bring us closer to the original signal, but since one of the objectives is to decrease nonparametric periodogram spectral leakage of a signal, it is desirable to have a window with the fewest possible samples but that provides relevant information about the original signal.
Figure 21 shows higher resolution by increasing the number of samples of the windows used in the Welch periodogram. In the aforementioned figure, the effects of the overlap recommended when using the Welch periodogram are presented. The results are as predicted by the theory, there is a decrease in the magnitude of the leakage―though with little significance for this example―when using an overlap of 75% in the rectangular windows employed.
Prabhu [12] suggests: “The resolution can be defined as the 3 dB bandwidth of the data window…”.
Even though there are no clear methods to determine the minimum size of a window, the 2013 version of Matlab in the path Signal Processing Toolbox/User Guide/ Statistical Signal Processing/Spectral Analysis/Nonparametric Methods states that
Resolution refers to the ability to discriminate spectral features, and is a key concept on the analysis of spectral estimator performance.
In order to resolve two sinusoids that are relatively close together in frequency, it is necessary for the difference between the two frequencies to be greater than the width of the mainlobe of the leaked spectra for either one of these sinusoids. The mainlobe width is defined to be the width of the mainlobe at the point where the power is half the peak mainlobe power (i.e., the 3 dB width). This width is approximately equal to![]() .
.
In other words, for two sinusoids of frequencies ![]() and
and![]() , the resolvability condition requires that
, the resolvability condition requires that
![]() (8)
(8)
![]()
Figure 21. Nonparametric Welch periodogram, window with 2048 samples, applied with different overlap percentages.
If the Matlab suggestion is applied to the example of two sinusoids separated by 10 KHz, the value obtained for L is
![]() (9)
(9)
However, as Figure 19 shows, L = 512 cannot resolve the two nearby frequencies.
6. Conclusions
In this paper, an inequality is proposed to determine objectively the minimum size of a window, instead of the trial and error technique commonly used. The results can be applied in particular to certain spectral estimators, better known as nonparametric periodograms.
It is also shown that the minimum size of a window is required to observe all the frequency components of a given signal; it is necessary that the frequency resolution should be considered when a signal is acquired and not only the Nyquist theorem.
Once the minimum size of a window has been evaluated, the relative amplitude of the frequency components and window type would be factors to be considered depending on the leakage they produce.
This work leaves behind the subjectivity to determine the minimum size of a window, merely by considering the desired resolution, which is now possible to assess objectively by controlling the number of samples and the sampling frequency.
The resolution ![]() is a parameter that, when considered before acquiring, optimizes the software or the hardware being used.
is a parameter that, when considered before acquiring, optimizes the software or the hardware being used.
The consideration and evaluation of ![]() will end to the ambiguity of ad-hoc “methods” employed in various signal processing tools to determine the minimum size of a given window, by using Equation (2) and Equation (3).
will end to the ambiguity of ad-hoc “methods” employed in various signal processing tools to determine the minimum size of a given window, by using Equation (2) and Equation (3).
Harris [1] concludes “We have demonstrated the optimal windows (Kaiser-Bessel, Dolph-Chebyshev, and Barcilon-Temes) and the Blackman-Hams windows perform best in detection of nearby tones of significantly different amplitudes”. This paper shows that, in addition to the type of window used, there are factors―as important as this one―that thwart the visualization of adjacent components, such as the difference in amplitude among components and the minimum size of a window.
Acknowledgements
This work was supported by DGAPA; PAPIME PE110216 Project “Propagación de ondas en medios sólidos, fluidos y gases”.