Estimating Crash Rate of Freeway Segments Using Simultaneous Equation Model ()
1. Introduction
Geometric conditions on freeways influence the occurrence of crashes. For instance, ramp spacing could be too short to provide sufficient space for drivers to negotiate with other competing drivers for maneuvers such as lane changes. Shoulders and median could have different impacts on driver behavior. When they are too wide, drivers may be encouraged to drive faster than expected which would cause speeding and the related crash. When they are too narrow, drivers may not have sufficient space to accommodate some sudden and magnificent movements, which would cause crashes.
It also has been observed that crashes generated on adjacent freeway segments exhibit spatial correlation. Either a small number of crashes in one segment corresponds to a big number of crashes in an adjacent segment or vice versus. It might be observed that crashes occurred on one segment cause congestion that migrates to the segments upstream which then cause secondary crashes. The migration to upstream segments depends on the severity of crashes downstream and the length of segment downstream. If the segments downstream are short and the crashes that happen there are severe, it would be expected to see the migration of congestion to upstream. In the other case, the congestion caused by crashes would remain local. This migration is also dependent upon whether or not there are traffic controls at the on-ramp entering the segment downstream. If there is ramp metering, traffic entering the segment containing a crash can be controlled. If traffic information is disseminated faster and taken by travelers, traffic may divert to other routes instead of passing the segment containing the crash.
Currently the models that estimate and forecast the number of crashes consider the conditions at one segment only; not including the nearby segments and their corresponding crashes. The correlation of crash frequency in space will likely invalidate the underlying assumption in current modeling, i.e., observed crash frequency is assumed independent across freeway segments. It can be imagined that the crash frequency forecast using these models will be biased and inefficient. Thus, due to the spatial adjacency nature of crash frequency observed, it is imperative that new models are developed that can consider the correlation between crashes in adjacent freeway segments.
In this study, simultaneous equations models were adopted to integrate the correlation of crashes on contiguous freeway segments. In one approach, two simultaneous equations were considered, one equation for one segment and the other for the upstream segment. In the second approach, three simultaneous equations were developed where the segments downstream and upstream of one freeway segment were considered. Three stage estimation methods are adopted to calibrate the models. The results from these models were interpreted and compared with the models where no simultaneous equation model was adopted, allowing conclusions to be made on the simultaneous equation modeling approach.
It should be noted that some studies have already developed models to address the spatial correlation of crashes on adjacent freeway segments. However, this study is the first where simultaneous equation models are employed to capture this spatial correlation. This approach is more straightforward than previous models because it does not require measures that represent the spatial proximity of the segments.
The following sections are organized as follows. The first section provides a literature review on crash frequency modeling. In the second section, the simultaneous equation modeling approach is introduced. The third section describes the data collection for model development and presents modeling results. In the last section, conclusions are made.
2. Literature Review
Researchers investigating the occurrence of crashes on freeway facilities usually use statistical models to quantify the relationship between crashes and influencing factors. Influencing factors in these studies mostly include geometric variables, traffic characteristics, as well as human factors.
The study in [1] defined freeway section by curve radius and classified the section by presence of ramps. Variables included number of lanes and median type, which were related to crash frequency. Their results indicated that geometric features had a significant impact on the crash frequency. The study in [2] examined crashes observed on three types of weaving sections categorized on the basis of the number of lane changes used by merging and diverging vehicles. Their results indicated that vehicle conflicts during off-peak periods and on wet roads, and the disparity between the speed of the movement requiring lane changes and that of the through and non-lane change merge raised safety issues on these sections. They also found that vehicle conflicts that tend to occur in the left lane during weekday rush hours were attributed to the safety performance of sections in which weaving movement can be made without any lane change.
The study in [3] showed a reduction in high severity crashes on freeway segments with an increase of barrier presences portioned to either side of a freeway segment. Median barrier and shoulder barrier lengths are measured and divided by twice the length of freeway segments. Freeway segments with both median and shoulder barriers running alongside the entire segment would result in a ratio of 1.0. If a segment has median barriers along the entire length but no shoulder barrier, a ratio of 0.5 results. Ratios from 0.5 to 1.0 in turn correspond to a reduction of fatality crashes from 6.5% to 5.7%, respectively. The study in [4] proved a two feet increase of shoulder width reduces fatal and injury crashes by 10%. However, this reduction was only for ramp influence areas of 0.3 miles upstream and downstream from painted gores.
The study in [5] related shoulder width to crash frequency. The effects of narrow shoulder width had shown to increase crash frequency on Las Vegas freeways. Their crash prediction model also included the minimum number of weaving lanes. The presence of auxiliary lanes insures at least two lanes are used in weaving movements. Weaving movements have long been a source of accidents due to the nature of competing lane changing. Results from [6] prove that designing a two lane off-ramp without the lane change option can reduce fatal crashes by 0.2% (all other crashes by 3.6%) when compared to traditional parallel off-ramp design. By eliminating the option to exit at the painted gore, a two-lane off-ramp decreases the need for weaving movements just before the off-ramp.
The study in [1] related safety and geometric design that includes ramp density and horizontal curves. The freeway sections with horizontal curves were recorded with many attributes such as number of lanes and median type. The results clarified the risk associated with the presences of exit and entrance ramps. The study in [7] pointed out that lane width, median width and shoulder width influence driver comfort, which has been known to affect crash rate. Grade changes on freeway segments at 4% increased crash rate by 20% when compared to lower gradients. The study in [8] investigated the impact on safety of freeway characteristics such as interchange spacing, shoulder widths and number of lanes. Their models show a large sensitivity to freeway and ramp Annual Average Daily Traffic (AADT) when predicting fatal and injury crashes.
2.1. Simultaneous Equation Model
The simultaneous equation model (SEM) is a structural model in which the interrelationship of variables forms a system of equations. For crash rate prediction, a system of equations can be written as follows:
(1)
where y is the vector of endogenous crash rates, Y is the vector of fitted endogenous crash rates with α estimated using instrumental variables, X is a matrix of exogenous geometric characteristics and traffic volumes with coefficients, β, and u is the error term assumed to be uncorrelated across observed values. The contemporaneous correlation across equations for the combined observations is used to obtain the covariance matrix of contemporaneous correlation error terms used in SEM estimation techniques. The covariance matrix is given as follows:
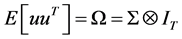(2)
where ∑ is the covariance matrix with I, the identity matrix for the T number of observations in each equation.
If least squares estimators are adopted, they do not converge on the probability of being an unbiased estimator as the number of observations increases [9] , and thus they are not consistent. In this case, instrumental variables are adopted which allows for improvement of regression estimates as long as the assumptions are met: they must be correlated with the included exogenous variables and have no correlation with the error term. The system of equations must be identified according to Equations (3), (4) [10] .
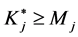(3)
(4)
where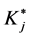 
= number of equation exogenous variables excluded, Mj = number of equation endogenous variables, K = total number of system exogenous variables, Kj = number of equation exogenous variables, M = total number of system endogenous variables = total number of equations, 
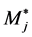= number of equation endogenous variables excluded.
In this study, three-stage least squares method [11] was adopted. In the first stage, instrumental variables Yi, the crash rate from each segment type (i.e., endogenous variables) is to regress all exogenous variables using OLS. The exogenous variables, Xi, are the geometric characteristics and traffic volume. The instrumental variables are used in the opposing equation for residual analysis. The residuals must be contemporaneously correlated. The second stage is calculating the covariance matrix using the residuals from the included instruments. In the third stage, the covariance matrix is used to estimate parameters using generalized least squares for the equation system in Equations (5), (6).
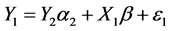(5)
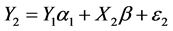(6)
The results from 3SLS, as long as the disturbances are contemporaneously correlated, are consistent estimators which are asymptotically more efficient [12] [13] .
2.2. Data Collection
The data set used for modeling was collected from the freeway system in the Las Vegas area in Nevada. It includes number of lanes, shoulder width, median shoulder width, average grade change, curve radius, and segment lengths. Table 1 includes the variable designations along with their units. The crash data were obtained from Nevada Department of Transportation and the crash rate was calculated according to Equation (7) and treated as an endogenous variable:
(7)
where N = number of crashes, V = AADT, and L = segment length in miles.
All measurements were taken using Google Earth imagery 2010. Freeway segmentations for EX-EN and EN-EX were made following the guidance in AASHTO 2001. The
![]()
Table 1. Description of variables used in modeling.
length of a segment was considered from the painted gore of the first ramp terminal to the painted gore of the next ramp and treated as base length according to HCM (2010). Freeway segments with ramp pair combinations of EX-EX and EN-EN as well as any work zone construction observed for 2010 was excluded. To relax accuracy issues when taking measurements, multiple measurements were taken and an average was recorded.
To simplify measurement, each horizontal curve observed was treated as a simple curve. Arc and chord length were recorded in Google Earth. The use of ArcGIS Curve Calculator under the COGO toolbar provided curve radii. When the same freeway segment encountered multiple curves, the shorter radius was recorded due to the stronger effect on driver comfort. This reasoning was considered for segments containing both curve radius and tangent sections. Some freeway segments shared curve radius. In this case, every segment was designated with the same curve radius measurement.
Average annual daily traffic (AADT) data was taken from the Nevada Department of Transportation. When spot volumes were not included in their traffic report, a balance approach was considered so that all freeway segments in the study had AADT values in the data set. The ramp AADT along with traffic volumes on contiguous segments were used in the balance calculations.
Freeway segments were paired initially by EX-EN segment and the following (or downstream) EN-EX (see Figure 1). The correlation of crash frequencies between these two segment types was observed.
Three segment clusters were formed by adding the upstream EN-EX to the paired segments (see Figure 1). The three segments together form a heterogeneous semi-cor- ridor in which explanatory variables differ across segments. The effects of the interchange are better understood with the upstream and downstream basic/weaving freeway segments (EN-EX) included in modeling. Each connected segment was modeled as one equation in the SEM. The descriptive statistics for that equation are listed in Table 2.
It can be seen from Table 2 that the crash rate of the EX-EN segments is higher than that of the EN-EX segment. It should be noted that the EX-EN segment length is shorter
![]()
Figure 1. Demonstration of combining successive freeway segments.
![]()
Table 2. Descriptive statistics for connecting segment types.
than that of EN-EX segments. These two segments have similar number of lanes, should width, median width, AADT. Their grades and radii are quite different.
3. Results and Discussion
3.1. The SEM Models for Paired Segments
The model was estimated adopting three-stage least squares method using R software and the results for the paired segments is indicated in Table 3.
It is obvious from Table 3 that the factors influencing the segments at interchanges (EX-EN) and those between interchanges (EN-EX) are different. It is because these two types of freeway segments are fundamentally different in geometry and traffic, one with reducing traffic, and the other with merging traffic on auxiliary lane. The variable Crash rate represents the correlation between these two types of segments when they are contiguous. Its coefficient is negative, implying that higher crash rate downstream would cause lower crash rate upstream. It might be due to the case that drivers upstream tends to slow down when they perceive a higher likelihood of crash downstream. AADT is another variable that can present the correlation between these two types of freeway segments. The coefficient for AADT on the interchange segment is positive while that for the between-interchange segment is negative. The positive coefficient implies that the increase of AADT has long been accredited to increases in crash rate. The more volume experienced in the same freeway facility increases the chance for vehicle crashes to occur. The small coefficient indicates that for every increase of AADT by 100,000 vpd, while holding all other variables in the EN-EX equation constant, would increase crash rate by 0.1 mvmt. On the between-interchange segments, the negative AADT coefficient might be due to the EN-EX segment already experiencing high volumes compared to EX-EN. An increase of AADT in an already high volume situation would increase to near jam capacity, which may in turn reduce crashes by impeding all vehicle maneuvers. The shockwave effects are felt upstream in the EX-EN segment that increases crash rate.
In the paired segment model, shoulder width, median shoulder width, AADT and curve radius were found significant in the estimated EX-EN model equation. Any increase in shoulder width and median width would decrease crash rate, which is reasonable. Widening these areas of the freeway would decrease the chance of vehicle collision when drivers make abnormal driving actions. Table 3 also shows that crash rate decreases with curve radius increasing, which is consistent with intuition. Larger radius makes the curves smoother, which would make driving easier on the curve.
In the EN-EX model equation, the shoulder width and curve radius have the same impact on crash rate as on the EX-EN equation. However, the median shoulder width was not found significant at the 95% level.
3.2. The SEM for Three Segments
The SEM model for three sequential freeway segments, up-stream EN-EX, EX-EN and down-stream EN-EX are indicated in Table 4. The number of segments decreased to 58 due to the limiting possibility of the three segments not being interrupted by an EN-EN or EX-EX segment. Shoulder width and median shoulder width are the only variables significant for each estimated segment equation. Increases in these variables decrease crash rate for all equations, which is the same for the paired segment SEM model.
From Table 4 it is clear that more factors influence the crash rate on the interchange segments than those on the between-interchange segments, which clearly indicates that it is important to develop different models for different types of freeway segment. AADT and radius are very significant for the interchange segments because these segments are relatively short. Any vertical and horizontal geometric changes would have more significant impact on these segments than on the relatively long between-inter- change segments. The endogenous parameter is significant which still shows that these contiguous segments are correlated. Only the EN-EX upstream model equation has segment length as a variable. The negative coefficient indicates that if segment length is decreased by 100 feet, then annual crash rate would increase by 0.008 mvmt if all other
variables are held. This result is reasonable and very important because the distance between interchanges should not be continuously decreasing. In Las Vegas, many interchanges have been built in recent years by adding interchanges between two existing interchanges, shortening the distance between interchanges. This result on segment length provides a way to quantify the impact of interchange space on traffic safety. This result cannot be obtained from other models.
The EX-EN estimated model equation exhibited an additional variable of average percent grade change compared to the previous paired segment model. The positive coefficient indicates that if average grade is increased by 1% then crash rate is increased by 0.127 when holding all other variables including those in the other equations. This observation is very revealing because it is clearly indicated that an interchange should be built on flater ground. Usually freeways are underpass. With high grade on interchange, the driving condition would not be favorable.
3.3. Model Comparison
Table 5 shows the comparison of SEM paired model to multiple linear regressions (MLR) of individual crash rate prediction models: One MLR equation for EX-EN and a separate model for the connecting downstream EN-EX. The estimates for the paired model have slightly more standard error when predicting their respective crash rate compared to MLR. However, more consistent estimators are seen with the addition of variable parameters when using SEM. For example, the variable Shoulder has a positive coefficient in the MLR model, implying that more crashes would occur when shoulders are widened, which contradicts common sense. Modeling crash rate simultaneously
with the use of instrumental variables has provided more information for freeway segments. SEM usage for this study proves the interrelatedness of connecting EX-EN and EN-EX segments.
4. Conclusion and Future Study Needs
4.1. Conclusions
The freeway segment at an interchange and those between interchanges are different, one with traffic exiting off the ramp, and the other with traffic entering from the ramp. They are correlated when they are contiguous which implies that some traffic would be continuous through both of them. When a crash happens downstream on the between- interchange segment, congestion would be formed and move upstream, which would influence the traffic conditions on the interchange segment. These observations make it imperative to look at the occurrence of crashes on these two contiguous segments simultaneously, which calls for employing simultaneous equation models estimating crash or crash rate on these freeway segments.
In this study, SEM models for paired freeway interchange segment EX-EN and downstream between-interchange segment EN-EX and those with combined three segment upstream EN-EX, EX-EN and downstream EN-EX have been developed. The endogenous variables have significant coefficients which indicate that unobserved variables exist on these contiguous segments, resulting in different crash rate. AADT is a variable that can show the interaction between the traffic and crashes on these segments. The results clearly present such an interaction. By comparing the SEM model and the MLR model, it is shown that more model parameters in the SEM models are significant than those from MLR. This further demonstrates the existence of the correlation between the interchange and between-interchange segments. It is important that some variables like segment length can be identified as significant in the SEM model, providing a way to quantify the safety impact of freeway development.
4.2. Future Study Needs
The Highway Safety Manual in [14] suggests using more than three years of safety data in order to notice the up- and-down trends of crash frequency not related to the changes in physical freeway characteristics. Once the average trend is observed, the corresponding crash frequency can be taken as the predictor variable. This suggests that more extensive study can be conducted by using more than one year of safety data.
The impact of using simultaneous equation model in forecasting crashes should also be investigated. Current crash forecast models do not consider the correlation of the crashes on contiguous freeway segments. This practice would cause crashes to be predicted unreliably. This unreliability should be quantified by comparing the SEM and non-SEM models.
Some factors like segment length are shown to be statistically significant, which actually cannot be identified using other models. The impact of these factors on safety should be further investigated to determine the linearity of this impact. Real cases in Las Vegas, Nevada can be used in quantifying the impact of intensifying freeway network on safety. Other variables such as shoulder width, AADT and crash rate on other contiguous segments can also be further investigated.