1. Introduction
Bio-excitations interaction with living organization of our body appears many non- linear effects, which is a significant issue studied in biophysics, bio-photonics, or even life sciences [1] . In early 1973, Davydov has proposed protein molecules excited “solitary” model of the energy transport [2] - [4] . According to his theory, three spiral micro- vibration and lattice distortion of amide-I exciton in a protein molecule produce collective excitations to form a soliton, along the helix propagation, so that the adenosine triphosphate (ATP) molecules are hydrolyzed to produce energy from one place to another place. This can be found in the experiment that soliton resonance light decomposes into excitons and local deformation, corresponding to a new band in 1650 cm−1, with amide-I exciton infrared absorption spectra observed on the 1666 cm−1 line, which demonstrates that there is a red shift of 16 cm−1 corresponding to the formation of just soliton bound energy. However, Davydov soliton seems to appear that short time span is serious obstacle to explain why it is a basic unit of energy and information transmission in bio-systems. For improving this weakness of the model, many scholars proposed modified models [5] . After that, Pang Xiaofeng improved and developed the Davydov soliton model with longer life span and established a sort of biological soliton transmission theory based on his nonlinear quantum theory [6] , by which Pang Xiaofeng showed that the revised Davydov solitons could play a basic metabolism role in energy and information transmission of bio-systems including human body.
In this work, we propose a model of oscillation of the Davydov solitons, via an acupuncture system (so called medial vein), in three wells of potentials to simulate the Davydov solitons condensation in three areas of living system. The author hopes this studying is constructive to allow us understand that there may exist three condensations of solitons restricted in three areas in human body, which may provide a possible mechanism to explain working nature of three acupuncture points, i.e. upper, middle and lower Dantian as described by Chinese medicine and acupuncture theory [7] .
2. Model of Oscillation
Let us consider a Davydov bio-vibration system in our body which is described by a nonlinear Schrödinger equation [8]
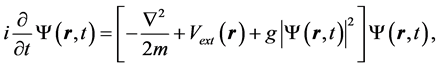 (1)
(1)
where g is a coupling number, the wave function 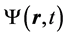 is supposed to be divided into three parts to oscillate (via a so called medial vein) among three potential wells. Here, the medial vein is one of parts of the acupuncture system, which passes through three acupuncture points described by the upper, middle and lower Dantian [7] . Then,
is supposed to be divided into three parts to oscillate (via a so called medial vein) among three potential wells. Here, the medial vein is one of parts of the acupuncture system, which passes through three acupuncture points described by the upper, middle and lower Dantian [7] . Then, 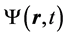 is expanded as
is expanded as
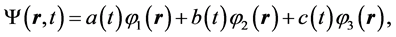 (2)
(2)
where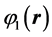 ,
, 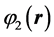 and
and 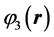 is a basic wave function in three wells, respectively, while
is a basic wave function in three wells, respectively, while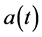 ,
, 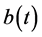 and
and 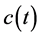 are correspondingly probability amplitude, with
are correspondingly probability amplitude, with
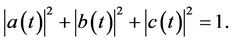 (3)
(3)
By instead Equation (2) into Equation (1), we obtain
 (4)
(4)
which can describe oscillation of soliton in three wells, where the relevant parameters are defined by
 (5)
(5)
 (6)
(6)
and
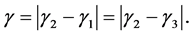 (7)
(7)
3. Solution of the Equation
Then through observation, the solution for Equation (4) can be approximately constructed by
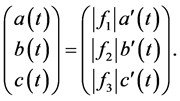 (8)
(8)
Then replacing Equation (8) into Equation (4), we can get
 (9)
(9)
This gives
 (10)
(10)
and
![]() (11)
(11)
The first Equation (10) can be simplified as
![]() (12)
(12)
where the physical meaning of ![]() and
and ![]() are approximately proportional to the rate of average occupational number of quasi-particles in the wells,
are approximately proportional to the rate of average occupational number of quasi-particles in the wells,
![]() (13)
(13)
here![]() ,
, ![]() ,
, ![]() is the average occupying quasi-particle number in three potential wells, respectively. Thus, the solution of Equation (12) is approximately gotten by
is the average occupying quasi-particle number in three potential wells, respectively. Thus, the solution of Equation (12) is approximately gotten by
![]() (14)
(14)
where![]() ,
, ![]() , and
, and ![]() are three integral constants which can be determined by the initial conditions
are three integral constants which can be determined by the initial conditions![]() ,
, ![]() , and
, and![]() . For instance, if the average occupational number is equal with each other in three wells then
. For instance, if the average occupational number is equal with each other in three wells then![]() ,
, ![]() and
and ![]() are determined by
are determined by
![]() (15)
(15)
here the conditions ![]() and
and ![]() have to be considered for the above Equation (15) to have mathematical meaning.
have to be considered for the above Equation (15) to have mathematical meaning.
On the other hand, for solving the second Equation (11) it is obviously to have
![]() (16)
(16)
![]() (17)
(17)
and
![]() (18)
(18)
Therefore, we eventually obtain the solution ![]() and
and ![]() by combining Equations (16)-(18) with Equation (14), namely
by combining Equations (16)-(18) with Equation (14), namely
![]() (19)
(19)
This shows that the oscillation posesses complicated frequency distributions and therefore it is not a Josephson oscillation as![]() ,
, ![]() , and
, and ![]() with the period
with the period
![]() , for
, for ![]() [8] - [10] . Secondly, the initial distribution of the average oc-
[8] - [10] . Secondly, the initial distribution of the average oc-
pying quasi-particle numbers for the oscillation ![]() in three potential wells should be not equal to 0, for instance, if they are equal with each other in three wells, i.e.
in three potential wells should be not equal to 0, for instance, if they are equal with each other in three wells, i.e.
![]() (20)
(20)
then the total oscillation will take part in three big solitons confined in three wells, respectively, which are described by Equation (19).
4. Conclusion and Remarks
In conclusions, the above model can be used in simulation of circle of some nonlinear excitations moving in the acupuncture system in advanced level, such as meaning of qi (here can be understood that the Davydov solitons is a kind of qi) moving in the medial vein and oscillation in three Dantians. The calculation shows that this sort of oscillation is possible if the initial rate of average occupational number of the quasi-particles in the wells is not equal to zero. One of simple oscillations arising relies on the initial rate of average occupational number of quasi-particles to be equal with each other within three wells, then the oscillation is not a kind of Josephson oscillation and has complicated frequency distributions, however the total behavior of oscillation played is similar to three big solitons concentrated in three wells. In the same way, the model of oscillation can be extended to oscillation over three wells system, such as oscillation in seven wells, to mimic working function of complicated medial vein + circle system which is also described by the theory of ancient Indian Yoga. In this sense, this model generally reveals a sort of oscillation mechanism of acupuncture system to working in our body, and explains clearly what means oscillation of qi, i.e. oscillation of Davydov solitons. This allows us to propose an assumption: there is no clear bio-structure (in the level of anthropotomy) and only has functional structure for acupuncture system. The oscillation of various excitatoins [11] falls into the acupuncture system, by which the information and energy can be transmitted to many places of the body and returning message is also the feedback for regulating the body. This is an oscillation which may be one of fundamental natures of our acupuncture system. We hope this studying could expose certain physical essences of the circle of qi in three Dantian via the medial vein for helping practitioners to increase their level.