Computer Simulation of Transition Regimes of Solitons in Four-Photon Resonant Parametric Processes in Case of Two-Photon Resonance

Vladimir Feshchenko¹, Galina Feshchenko²

¹Dawson College, Montreal, Canada.
²Vanier College, Montreal, Canada.

DOI: 10.4236/ajcm.2016.63028                

Abstract

The transition regimes of solitons in four-photon resonant processes in the case of two-photon absorption of the fundamental radiation are numerically investigated. The standard system of equations for the amplitudes of probability of finding the system in state with certain energy is used to derive the expression for the induced polarization in the nonlinear medium. As for the equations for the amplitudes of the optical pulses, the general case is considered in which both the amplitudes and phases are space-time dependent. We focus on the finite difference methods and the case of simultaneously propagating solitons at all frequencies of the interacting waves (simultons). The obtained results indicate that upon certain threshold conditions all interacting pulses become the solitons of Lorentzian shape. The numerical analysis has also shown that the soliton amplitudes significantly depend on the ratio between the nonlinear polarizability at the fundamental frequency ω₀ and that of combination of ω₀ and the trigger-field frequency ω₁(2ω₀ + ω₁). In the second part of the paper, we apply the method of phase planes to show that at typical values of parameters, the solitons are stable.

Keywords

Solitons, Transition Regime, Stability

Received 30 July 2016; accepted 20 September 2016; published 23 September 2016

1. Introduction

Solitons or self-reinforcing solitary waves can emerge spontaneously in a physical system in which some energy is fed in, for instance as thermal energy or by an excitation with an electromagnetic wave, even if the excitation does not match exactly the soliton solution. Therefore, if a system possesses the necessary properties to allow the existence of solitons, it is highly likely that any large excitation will indeed lead to their formation [1] - [3] . The field of solitons and related nonlinear phenomena has been substantially advanced and enriched by research and discoveries in nonlinear optics [4] - [7] .

In our previous research [8] , we established the possibility of the existence of simultons (simultaneously propagating solitons at different frequencies) in the case of nonstationary Raman scattering with excitation of polar optical phonons under the conditions of the interaction of ultrashort pulses of exciting and Stokes radiation in nonlinear crystals. The relevance of this study is connected both with the fact that one can extract additional information on the optical characteristics of matter, and with the possibility of obtaining of ultrashort pulses.

The second topical problem in modern nonlinear optics is the production of coherent and frequency-tunable radiation in the far ultraviolet (UV) and infrared (IR). In these spectral areas, solid materials have broad absorption bands and this narrows down the application of nonlinear crystals for the generation of electromagnetic radiation. Possible ways of overcoming those difficulties are related with the utilization of nonlinear phenomena in gases and metal vapors. The resonant four-photon interaction (RFPI) in the case of two-photon resonance is one of them. Among the advantages of gases are the presence of narrow resonances and possibility of continuous variation of density, width of spectral line, length of the medium, etc. [9] - [11] . Ultrashort pulse propagation in the case of two-photon resonance was first examined in [12] where the two-photon self-induced transparency effect was predicted. This prediction was subsequently confirmed experimentally [13] and by numerical studies [14] . Third-harmonic generation (THG) in media exhibiting resonance behaviour has also attracted considerable attention [15] - [21] . However, RFPIs that are not frequency degenerate are of no less interest; they can be used to transfer the tuning of radiation from one range to another [22] [23] .

The present paper is devoted to the computer simulation of transition regimes of RFPI solitons in the case of two-photon resonance. The basic equations describing this process are given in Section 2 [12] [24] . The results of computer simulation are shown in Section 3. The stability of solitons is considered in Section 4.

2. Fundamental Principle

Let us assume that two optical pulses with frequencies propagate in the nonlinear medium at the angles 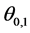with respect to the z-axis. The value of 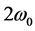is close to the frequency of resonant transition between levels 2 and 1 in the medium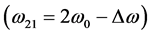. The nonlinear interaction between 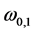and the medium results in parametric generation of 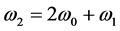and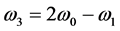. The values of are considered to be in the transparent range of frequencies. We also assume that all electromagnetic waves have the same polarizations.

To find the system of equations that governs the processes of propagation of optical pulses with frequencies in the medium we take the standard system of equations for the amplitudes of probability of finding the system in state with energy [25]

(1)

where (2)

is the dipole moment of the transition; are the frequencies, wave vectors, real “slowly-varying amplitudes”, and phases of the interacting waves, respectively.

We next use (1) and the theory of perturbations [26] to find (the perturbation coefficient is of

order)

(3)

To obtain the system of equations for we introduce the expression (3) into the Equation (1), which becomes

(4)

(5)

where

.

The expression for the polarization induced by the superposition of nonlinear waves is defined by

. (6)

We introduce (3) into (7) and find that the expression for the induced polarization becomes

(7)

where , ,

The system of Equations (4) and (5) can now be rewritten in terms of and n as follows

(8)

(9)

(10)

where , , is the maximum pulse amplitude; is the pulse width.

To make the system (8) - (10) complete we add Maxwell’s equations for the all real “slowly-varying amplitudes” and their phases. We obtain

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

where

, N is the number of molecules in cm³,.

3. Transition Regime

We carried out the computer simulation of the system (8) - (10) and (11) - (18) for the following parameters of electromagnetic radiation and medium (gases): and [27] - [29] . The optical pulses on the pump and trigger frequencies were chosen to be of Gaussian shape. The accuracy of numerical results was based upon monitoring the conservation of energy of the system at every cross-sectional area in the medium. We considered the following trends: the phase locking and confinement; the length of medium needed for soliton formation; the distribution of energy during the transition regime; the energy limitations on solitons formation; the effect of slowing down of solitons in resonant systems; the relationship between the soliton speed and characteristics of incoming electromagnetic waves and nonlinear medium; the conditions leading to formation solitary wave at one frequency (instead of generation of sequence of them); the connection between the amplitude of soliton and parameters upon consideration. The space-time evolution of the normalized intensities (, , , and) is shown in Figures 1-4.

4. Stability

To investigate the stability of solitons we perform the summation of the Equations (12) (14) (16) and (18) for phases and transform them to the equations for. We assume that both processes occur at the conditions of synchronism, so that and. This condition is usually satisfied in gases [29] . Moreover, we also suggest that the phase differences are locked to or due to the nonlinear effects [30] . In this case (). Let be or, where are some small phase fluctuations. Finally, the modified system of (12) (14) (16) and (18) can be written in terms of as follows

(19)

(20)

Figure 1. The formation of the soliton at frequency.

Figure 2. The formation of the soliton at frequency.

where ,

is the simulation velocity,

The behaviour of the latter system is analyzed in terms of phase planes. As an example, Figure 5 shows the phase plane of the following system

(21)

Figure 3. The generation of the soliton at frequency.

Figure 4. The generation of the soliton at frequency.

(22)

at 11 different initial conditions for.

5. Conclusion

The space-time evolution of the optical pulses by using the computer simulation of transition regimes of four- photon resonant parametric processes in case of two-photon resonance is investigated. The computer simulation was based on application of the finite difference methods to the system of nonlinear equations modeling the foregoing interactions. It is shown that at certain boundary conditions (those result from the “area theorem” (see, e.g. [30] )) the incoming laser pulses at frequencies first generate new waves at, and then all become simultons of Lorentzian shape. It has also been shown that upon the conditions of phase locking (

Figure 5. The phase plane of the system (21) and (22) (and) for 11 consecutive initial conditions for: = 2.0, 2.0; 1.9, 1.9; 1.8, 1.8; 1.0, 1.0.

or) and synchronism (and) in wide range of typical values of polarizabilities, the simultons are stable. These results could be useful for the applications related with designing the lossless communication systems using the tunable frequencies ranging from IR () to UV ().

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Dauxois, T. and Peyrard, M. (2010) Physics of Solitons. Cambridge University Press, Cambridge.
[2]	Williams, M.C. (2013) Solitons: Interactions, Theoretical, and Experimental Challenges and Perspectives. Nova Science Publishers Inc., New York.
[3]	Manevich, L.I. and Simmons, V.V. (2008) Solitons in Micromolecular Systems. Nova Science Publishers Inc., New York.
[4]	Dzedolik, I.V. (2016) Solitons and Nonlinear Waves of Photon-Polaritons and Plasmon-Polaritons. Nova Science Publishers, New York.
[5]	Boyd, R. (2008) Nonlinear Optics. 3rd Edition, Academic Press, Waltham.
[6]	Kivshar, Y. and Agrawal, G. (2003) Optical Solitons: From Fiber to Photonic Crystals. Academic Press, Waltham.
[7]	Abdullaev, F., Darmanyan, S. and Khabibullaev, P. (2013) Optical Solitons. Springer Publishing, New York.
[8]	Feshchenko, G. and Feshchenko, V. (2015) Computer Simulation of Transition Regimes of Solitons in Stimulated Raman Scattering with Excitation of Polar Optical Phonons. American Journal of Computational Mathematics, 5, 336-344. http://dx.doi.org/10.4236/ajcm.2015.53031
[9]	De Melo, N.R. and Vianna, S.S. (2014) Two-Photon Resonant Forward Four-Wave Mixing in Rubidium Vapor Involving Rydberg States. Journal of the Optical Society of America B, 31, 1735-1740. http://dx.doi.org/10.1364/JOSAB.31.001735
[10]	Namboodiri, V., Namboodiri, M., Flachenecker, G. and Materny, A. (2010) Two-Photon Resonances in Femtosecond Time-Resolved Four-Wave Mixing Spectroscopy: Beta-Carotene. The Journal of Chemical Physics, 133, Article ID: 054503. http://dx.doi.org/10.1063/1.3466750
[11]	Smith, A.V., Alford, W.J. and Madley, G.R. (1988) Optimization of Two-Photon Resonant Four-Wave Mixing: Application to 130.2-nm Generation in Mercury Vapor. Journal of the Optical Society of America B, 5, 1503-1519. http://dx.doi.org/10.1364/JOSAB.5.001503
[12]	Belenov, E.M. and Poluektov, I.A. (1969) Coherence Effects in the Propagation of an Ultrashort Light Pulse in a Medium with Two-Photon Resonance Absorption. Soviet Physics—JETP, 29, 754-756.
[13]	Tan-no, N., Yokoto, K. and Inaba, H. (1972) Two-Photon Self-Induced Transparency of Different Frequency Optical Short Pulses in Potassium. Physical Review Letters, 29, 1211-1213. http://dx.doi.org/10.1103/PhysRevLett.29.1211
[14]	Tan-no, N., Yokoto, K. and Inaba, H. (1975) Two-Photon Self-Induced Transparency in a Resonant Medium. II Transient Pulse Behaviour. Journal of Physics B: Atomic and Molecular Physics, 8, 349-357. http://dx.doi.org/10.1088/0022-3700/8/3/005
[15]	Wang, C.C. and Davis Jr., L.I. (1975) Saturation of Two-Photon Transitions in Thallium Vapor. Physical Review Letters, 35, 650-652. http://dx.doi.org/10.1103/PhysRevLett.35.650
[16]	Ward, J.F. and Smith, A.V. (1975) Saturation of Two-Photon Optical Processes in Cesium Vapor. Physical Review Letters, 35, 653-655. http://dx.doi.org/10.1103/PhysRevLett.35.653
[17]	Leung, K.M., Ward, J.F. and Orr, B.J. (1974) Two-Photon Resonant Optical Third-Harmonic Generation in Cesium Vapor. Physical Review A, 9, 2440. http://dx.doi.org/10.1103/PhysRevA.9.2440
[18]	Poluéktov, I.A. (1977) Third Harmonic Generation by Two-Photon Interaction of High-Power Coherent Light Pulses with Resonant Media. Soviet Journal of Quantum Electronics, 7, 364-365.
[19]	Anikin, V.I., Drabovich, K.N. and Dubovick, A.N. (1977) Coherence Effects in Optical-Frequency Summation under Two-Photon Resonance Conditions. Journal of Experimental and Theoretical Physics, 45, 906-911.
[20]	Maimistov, A.I., Manykin, E.A. and Khodulev, L.B. (1979) Propagation of Short Optical Pulses during Third-Harmonic Generation in the Case of Two-Photon Resonance. Journal of Experimental and Theoretical Physics, 49, 431-435.
[21]	Elgin, J.N. and New, G.H.C. (1978) Theory of Two-Photon Resonant Up-Conversion with Ultrashort Pulses. I. Third Harmonic Generation. Journal of Physics B: Atomic and Molecular Physics, 11, 3439-3451. http://dx.doi.org/10.1088/0022-3700/11/19/019
[22]	Matsuoka, M., Nakatsuka, H. and Okada, J. (1975) Free-Precision Decay of Two-Photon-Induced Coherence in Ca Vapor. Physical Review A, 12, 1062-1065. http://dx.doi.org/10.1103/PhysRevA.12.1062
[23]	Butylkin, V.S., Grigor’yan, V.S. and Zhabotinskii, M.E. (1980) Four-Wave Interaction of Ultrashort Light Pulses Propagating Successively in a Medium. Journal of Experimental and Theoretical Physics, 51, 832-838.
[24]	Takatsuji, M. (1975) Theory of Coherent Two-Photon Resonance. Physical Review A, 11, 619-624. http://dx.doi.org/10.1103/PhysRevA.11.619
[25]	Sakurai, J.J. and Napolitano, J. (2013) Modern Quantum Mechanics. 2nd Edition, Pearson, New York.
[26]	Davydov, A.S. and Haar, D. (2016) Quantum Mechanics. 2nd Edition, Science Direct, Amsterdam.
[27]	Butylkin, V.S., Kaplan, A.E., Khronopulo, Y.G. and Yakubovitch, E.I. (2012) Resonant Nonlinear Interactions of Light with Matter. Springer Science & Business Media, New York.
[28]	Makhviladze, T.M. and Sarychev, M.E. (1976) Soliton Regimes of Stimulated Raman Scattering. Journal of Experimental and Theoretical Physics, 44, 471-477.
[29]	Barantzov, V.I., Popov, A.K. and Tartakovskii, G.Kh. (1974) Possibility of Four-Photon Parametric Generation of Light in Gases. Journal of Experimental and Theoretical Physics, 40, 449-456.
[30]	Marchevskii, F.N., Strizhevskii, V.L. and Feshchenko, V.P. (1985) Solitons Formation in Resonant Parametric Processes in Gases. Bulletin of the Russian Academy of Sciences: Physics, 49, 606-610.