Knowledge Discovery in Learning Management System Using Piecewise Linear Regression ()
1. Introduction
Knowledge Discovery in Databases (KDD) is defined as the nontrivial process of identifying valid, novel, potentially useful, and ultimately understandable patterns in data [1] . It has become a very important process to all the businesses and organization since it provides useful information that is most important to the business and future business decisions. In order to discover the knowledge from large volumes of data, undoubtedly the term data mining pops up, since data mining is the field which can handle large volumes of data and can derive useful knowledge from it [2] - [4] .
As we live in a digital world, there is a steady increase in accumulation of structured and unstructured data from various sources such as transactions, social media, sensors, digital images, videos, audios and click streams for domains including healthcare, retail, energy and utilities. For instance observation [5] reveals that 3 billion contents are being shared on Facebook every month; the photos viewed every 16 seconds in Picasa could cover a football field. Such a massive volume of data storage is generally termed as “Big Data”. Turning big data into knowledge becomes a challenging task. However standard statistical methods cannot be made applicable directly to represent such huge data. Therefore the open challenge in big data is big data analysis which concerns in organizing and analyzing large sets of data to discover patterns and knowledge.
To incorporate new concepts in knowledge representation, Diday [6] has introduced a phrase called Symbolic Data Analysis (SDA). SDA refers to summarizing a large dataset in such a way that the resulting summary dataset is of a manageable size and yet retains as much of the knowledge in the original dataset as possible. These summarized data are termed as symbolic data [7] [8] . In general, it is contrasted with classical data in which each data point consists of a single (categorical or quantitative) value, where symbolic data can contain internal variation (list, ranges, etc.) and can be structured. In that very important sense, SDA can be considered a method for Big Data [9] .
Our objectives in this paper are to propose a new idea of histogram based piecewise linear regression method, to summarize very large datasets, to produce smaller datasets in order to enhance the data mining technique to mine knowledge pattern in big data. Section 2 presents a brief literature review about symbolic data analysis and provides reasons for selection of PLR. Sections 3 describes histograms based piecewise linear regression lines. Also we propose the distance measure between two piecewise linear regression features. Section 4 furnishes the case studies on online education system to evaluate and discover the knowledge. Section 5 provides conclusion.
2. Literature Review on Symbolic Data Analysis
As in [11] , interval data, multi-valued data and histogram data are described as major types of symbolic data. Histogram has been projected as a feature type, possessing the generality to characterize all other feature types like single valued, multi-valued, interval valued [10] . It has received significant attention as summarization/representative object. Moreover, interval data and multi-valued data [11] [12] are impossible to adapt all classical arithmetic formulations that apply to the single-valued data to interval-data without making the appropriate amendments. Hence we use histogram as the symbolic data to represent the concept descriptions. Subsequently, distance between the histograms has been proposed [13] - [15] in order to cluster a set of data described by distribution.
Also in the case of histogram there are some disadvantages. It is observed that algorithms for producing histograms are required to have the same number of bins and same bin width for all datasets for the effective characterization of data into histograms [16] . So storage of histograms requires memory for number of bins, bin width and memory for the details of each bin. Moreover by making a series of arithmetic operations on a number of histograms, the resulting histogram is expected to have a high number of intervals [17] .
To overcome the disadvantages, an idea has been proposed [10] [16] [17] to model the histogram through a suitable basis function. Therefore parameters for histograms such as bin width, number of bins etc will not be of concern. Simona Signorillo [16] [18] approximated histogram using a B-spline. The challenge in that is to choose the number of optimal knots. The other basis function used is linear regression line to model the histogram. This model drastically reduces the computational complexity which holds more details about the data in a compressed form which requires only two parameters-slope and intercept. Also it reduces the memory requirement. It is further shown that regression line is a powerful knowledge representative [17] [19] .
Analysis on regression model shows that, single linear regression line is not always “best fit” for the histogram model because it suffers from appropriateness by maximizing the sum of the squared residuals. To be precise, a single linear regression model could not provide an adequate description for generic databases and nonlinear model could not be appropriate either. Besides, its corresponding regression based distance measure would produce factual error. To overcome this problem, we propose a model using PLR [20] [21] to represent the shape of the distribution purified from the error.
3. Piecewise Linear Regression (PLR)
A problem which recurs occasionally is the estimation of regression parameters when the data sample is hypothesized to have been generated by more than a single regression model. This has been referred to as “piecewise linear regression” [22] .
To state our problem, consider Y as the response variable, and X as the explanatory variables. Assume that there is a sample of n observations. These observations are governed by a model of histograms. Our objective is to represent histogram by monotonic increasing piecewise linear regression with k segments separated by a breakpoint BP. The simplest piecewise-regression model joins two straight lines sharply at the breakpoint as follows:
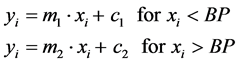(1)
where yi is the value for the ith bin, xi is the corresponding value for the independent variable, m1 and m2 are the slope of the line segments, c1 and c2 are the intercept at the y-axis. The present paper recommends the following procedure when fitting piecewise regression line.
3.1. Estimate Breakpoint
The major problem is to determine the number and location of the “break points” of the underlying regression systems. The procedure we employ is the examination of the first order derivative in histogram, similar to proposed by Howard Wainer [23] . Fundamentally, the strength of the response of a derivative operator is proportional to the degree of dependent variable discontinuity at that point at which the operator is applied [24] . Therefore the histogram differentiation enhances local slope where there is a lot of discontinuity information in the source and deemphasizes areas where there is little information in the source. It can be found between each successive bins i and i + 1 using 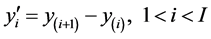(2).
(2)
where I is the number of bins. Hence the places where the first order derivatives 
are large are identified as breakpoints. Through empirical analysis on data points we can decide the number of breakpoints in accordance with the number of histogram bins.
3.2. Access Breakpoint
The next problem was to determine which of these points are break points and which are simply bad data point which caused a spuriously high first derivative. Let us say that breakpoint occurs at point j: we wish to determine if the parameters of the regression system determined by points 1 − j are significantly different from those of points j − n, where n is the total number of points. To do this we shall construct a confidence interval around m1 and b1, where m1 and b1 are the slope and the y-intercept respectively of the best fitting (in a least-squares sense) straight line for the points 1 − j. We then inspect our estimates of m2 and b2 (the same parameters, for points j − n) to see if they lie in the confidence interval. The uncertainty about the distribution of regression parameters indicates that the jackknife [25] - [27] would be useful to compute confidence intervals for the estimation of the parameter. The appendix contains a brief description of jackknifing.
It is clear that if a break point exists at all it is most likely that the first derivative is largest at that place. If, in fact, the regression systems about point j are different, one can continue the same process by examining the second largest first derivative and if it is below point j, say at point k, repeat the above procedure for points 1 − k and k − j. This can be continued until no further significant differences are obtained.
3.3. Fit PLR
In order to fit PLR, the histogram is converted to normalized cumulative histogram. Since the shape of the histogram is not monotonically increasing where cumulative histogram always has positive slope. The estimated break points are mapped at the respective position. Then, we shall connect each pair of adjacent points by a straight line, whose are represented by set of slopes and intercepts.
4. Piecewise Linear Regression Line Distance Measure
After having built the piecewise regression line, now this section proposes an approach to find distance measure between two piecewise regressions lines indeed distance between two symbolic objects. The key idea is to find the area between consecutive breakpoints.
4.1. Area Subdivision
Consider parallel lines from every break point to other end piece regression line, about the x axis. This is done to split the area into subareas.
4.2. Subarea Measure
Now each subarea has one pair of parallel sides about to x axis and a pair of linear regression lines about to y axis, hence each subarea can be considered as trapezium [16] . So area of trapezium characterizes the distance between two simple regression lines. For a pair of samples, two different cases are possible and are summarized below:
Case 1: When pair of lines are not intersected shown in Figure 1, area of trapezium A is given by the following formula where a and b are the lengths of the parallel sides and h is the perpendicular distance between the parallel sides.
(3)
![]()
where c1, m1 are the intercept and slope of simple linear regression line 1 and c2, m2 are the intercept and slope of simple linear regression line 2.
Case 2: When pair of lines are intersected shown in Figure 2, area of trapezium A is considered as two triangles where their heights are computed based on the intersection point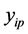 
between two lines
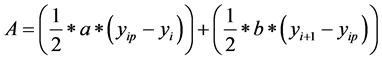(4)
![]()
where 
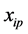and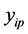 
are intersection points between pair of samples.
![]()
Figure 1. Pair of lines are not intersected.
4.3. Summation of Distance Measure
Distance computed from all sub region is summed up. A distance measure (also called a metric) is a dissimilarity Measure. The distance measure values closer to zero reveals that two symbolic objects have high similarity and vice versa.
5. A Case Study on Real Data
In this section, we propose a case study on real dataset. The case study refers to the quiz data pooled by a Learning Management Systems (LMS) called EkLuv-Ya [Ekl0] is used. EkLuv-Ya is the product created by Amphisoft Technologies for revolutionizing engineering education through Automated Evaluation Systems in different branches of engineering.
From the standpoint of the big data, the main objective of this case study is to show how the PLR summarizes the datasets in a meaningful and intelligent fashion, to its important and relevant features. Also how it enhances the data mining technique to mine knowledge pattern in big data. Hence we need to use a clustering technique in integration with SDA. Clustering is an unsupervised learning problem that group objects based upon distance or similarity. Each group is known as a cluster [28] .
5.1. Knowledge Pattern Discovery in LMS
A typical web based LMS such as moodle [29] [30] in its simplest form provides a platform for online learning where educators can post their learning materials, assignments, tests etc and monitor progress of their students who in turn have to log in to learn from the posted material. An LMS [31] can keep record of all the student activities through their log files which pave way to gather large amount of data on a day to day basis. The amount of data which is gathered is proportional to the number of students registered for each course, number of times each student logs in for each of the registered courses and number of courses that are handled by an LMS. We can find streams of log records getting generated every moment, which makes the real time knowledge extraction almost impossible.
The datasets under investigation is the quiz data. It contains the marks scored in different quizzes by the 52 students of sixth semester of Bachelor of Engineering from Aditya Institute of Technology, Coimbatore (Tamil Nadu), India. The subjects of study in the order of appearance are: Computer Graphics, Mobile Computing, Numerical Methods, Object Oriented System Design and Open Source Software. For the sake of experimentation, minimum marks for each quiz is 2 and maximum marks for each quiz is 10. Marks of students who could not take up the quiz in a particular subject have been marked as “1”. The total number of bin taken is ten which is proportional to the number of quizzes. For bin size 10, the number of break point fixed is 1.
Results and Discussion
The histogram matrix computed by summarizing the distribution of marks of ten quizzes under each of five subjects for every student is illustrated in Figure 3. Thereby providing users with the ability to visually analyze and explore large, complex datasets. The first derivatives were approximated and the largest derivative value location is determined.
Tukey’s “jackknife” is used to test the meaningfulness of that breakpoint. For illustration, the data are shown in Figure 4. The first derivatives were approximated and the largest derivative was at point 7; we therefore examined the regression line of points 1 - 6 and concluded, through jackknifing, that the parameters of the regression system were
![]()
Figure 3. Summarization of very large data sets into symbolic histogram feature.
![]()
Figure 4. Number of quizzes versus mark frequency.
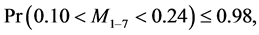
The points 8 - 10 were also jackknifed and yielded the following parameter estimates:
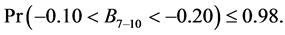
where M and B are the slope and the y-intercept of the regression line indicated. These two pairs of intervals do not even overlap and hence we concluded that point 7 was a break point.
Then histogram is converted to cumulative histogram Figure 5 and the breakpoint is mapped.
Piecewise regression line Figure 6 is fitted to the cumulative histogram according to the algorithm illustrated in the Section 3, which characterize the relationships and dependencies that exist within the histogram. Using AB distance measure dissimilarities between individual objects are calculated and the size of the matrix is 52 * 52 * 5.
The obtained distance matrix is given as input to cluster analysis [32] to classify them into groups. The strength of the distance measure is portrayed by the dendrogram (Figure 7) of the obtained data set. The dendrogram [14] shows the merging of samples into clusters at various stages of the analysis and the similarities at which the clusters merge, with the clustering displayed hierarchically. There are 2 major classes obtained in the structure (Figure 7). The students grouped in cluster 1 (blue) have secured mark
![]()
Figure 5. Cumulative histograms with breakpoints.
![]()
Figure 6. PLR features representing students performance.
![]()
Figure 7. Dendrogram obtained through complete linkage clustering using AB distance measure.
above 70% which indicates good knowledge in subjects. Cluster 2 (red) students below 70% who have poor knowledge in subjects. In order to validate, obtained results when compared with teachers handling the subjects match exactly with the expected results. This experimentation will help the teacher in finding out the students of a particular group and counsel them as the information about serial number of students is retained as knowledge. Also it promises to enhance academic planner’s sense of decision making which specific subject should be improved to achieve student learning effectiveness and progress [16] .
6. Conclusion
Big data are a new phenomenon. Also a characteristic of modern large-scale data sets is that they often have a nontraditional form. New statistical methodologies with radically new ways of thinking about data are required. In that very important sense, PLR can be considered a method for Big Data which holds more details about the data in a compressed form which requires only two parameters sets―slope and intercept. Also PLR a powerful knowledge representative, instead of a histogram reduces the memory requirement and the computational complexity of this symbolic histogram. We employed Tukey’s “jackknife” to test the meaningfulness of any suggested subdivision of the regression curve into pieces. To support our proposed theory we have done a case study in educational environment. It is expected that this work can be successfully used in different areas including financial, banking.