Alternative Fourier Series Expansions with Accelerated Convergence ()
1. Introduction
There is perhaps no better way starting the discussion than quoting directly from Iserles and Nørsett [1] : “By any yardstick, Fourier series are one of the greatest and most influential concepts of contemporary mathematics. … It is thus with a measure of trepidation and humility that we wish to pursue a variation upon the Fourier theme in this paper.” Since trigonometric series was first used by d’Alembert in 1747, the full formation of Fourier theories surprisingly took more than a century of endeavors highlighted by the famous d’Alembert-Euler-Bernoulli controversy and many important and/or pioneering contributions from Euler, Dirichlet, Lagrange, Lebesgue and other leading mathematicians of the time. Nevertheless, it was not long before mathematicians and scientists came to appreciate the power and far-reaching implications of Fourier’s claim that any function could be expanded into a trigonometric series. Fourier’s discovery is easily ranked in the “top ten” mathematical advances of all time.
Despite what has been said, the Fourier series will lose much of its luster when used to expand a sufficiently smooth nonperiodic function defined on a compact interval. It is well known that a continuous function can always be expanded into a Fourier series inside the interval (the word “inside” is highlighted to emphasize the fact that the two end points shall not be automatically included). This is actually the primary reason for the inefficiency of the Fourier series in approximating a nonperiodic function, and, understandably, in solving various boundary value problems. This work is aimed at overcoming the said difficulties associated with the conventional Fourier series.
It is known that a continuous function f(x) defined on the interval [−π, π] can always be expanded into a Fourier series
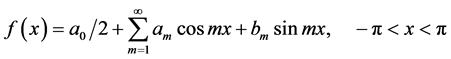 , (1.1)
, (1.1)
where the expansion coefficients are calculated from
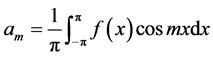 , (1.2)
, (1.2)
and
 . (1.3)
. (1.3)
The Fourier series, (1.1), reduces to
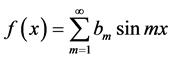 (1.4)
(1.4)
if f(x) is an odd function;
and to
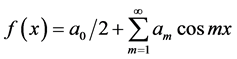 (1.5)
(1.5)
if f(x) is an even function.
The convergence of the Fourier series, (1.1), is well understood through the following theorems.
THEOREM 1. If 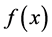 is an absolutely integrable piecewise smooth function of period of 2π, then the Fourier series of
is an absolutely integrable piecewise smooth function of period of 2π, then the Fourier series of  converges to
converges to 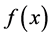 at points of continui-
at points of continui-
ty and to 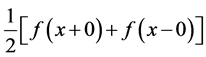 at points of discontinuity. If
at points of discontinuity. If 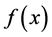 is continuous everywhere, then the series converges absolutely and uniformly.
is continuous everywhere, then the series converges absolutely and uniformly.
Proof. Pages 75-78 of Ref. [2] .
THEOREM 2. For any absolutely integrable function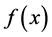 , its Fourier coefficients satisfy
, its Fourier coefficients satisfy
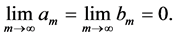 (1.6)
(1.6)
Proof. Pages 70-71 of Ref. [2] .
THEOREM 3. Let 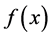 be a continuous function of period 2π, which has n derivatives, where n − 1 derivatives are continuous and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Then, the Fourier series of all n derivatives can be obtained by term-by-term differentiation of the Fourier series of
be a continuous function of period 2π, which has n derivatives, where n − 1 derivatives are continuous and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Then, the Fourier series of all n derivatives can be obtained by term-by-term differentiation of the Fourier series of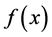 , where all the series, except possibly the last, converge uniformly to the corresponding derivatives. Moreover, the Fourier coefficients of the function
, where all the series, except possibly the last, converge uniformly to the corresponding derivatives. Moreover, the Fourier coefficients of the function  satisfy the relations
satisfy the relations
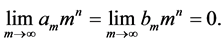 (1.7)
(1.7)
Proof. Pages 84, 130, and 131 of Ref. [2] .
As a matter of fact, (1.7) can be replaced by more explicit expressions [3] [4]
 (1.8)
(1.8)
and
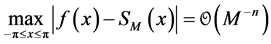 (1.9)
(1.9)
where ![]() is the partial sum of the Fourier series defined as
is the partial sum of the Fourier series defined as
![]() (1.10)
(1.10)
The aforementioned convergence theorems are established based on the condition that f(x) is a periodic function of period 2π. It is known that the Fourier series of an analytic 2π-periodic function can actually converge at an exponential rate [5] . However, once the periodicity condition is removed, the convergence of a series expansion can be seriously deteriorated or even there is no convergence in the maximum norm. When f(x) is defined only on a compact interval [−π, π], it can be viewed as the part of the 2π-periodic function which is the periodic extension of f(x) onto the whole x-axis. Thus, even f(x) is sufficiently smooth on [−π, π], the extended periodic function may only be piece-wise smooth due to the potential discontinuities at ![]() (
(![]() ). As a consequence, the series expansion of f(x) converges to f(x) for every x Î (−π, π), and to
). As a consequence, the series expansion of f(x) converges to f(x) for every x Î (−π, π), and to ![]() at x = ±π. Understandably, such a Fourier expansion converges very slowly.
at x = ±π. Understandably, such a Fourier expansion converges very slowly.
Assume, for example, that ![]() is continuous on [−π, π] with an absolutely integrable derivative (which may not exist at certain points). Then we have
is continuous on [−π, π] with an absolutely integrable derivative (which may not exist at certain points). Then we have
![]() (1.11)
(1.11)
where am and bm are the Fourier coefficients of ![]() and
and![]() . Since
. Since
the Fourier coefficients of an absolutely integrable function tend to zero as ![]() (Theorem 2), it is obvious that
(Theorem 2), it is obvious that
![]() , (1.12)
, (1.12)
and
![]() . (1.13)
. (1.13)
If![]() , then we have
, then we have
![]() (1.14)
(1.14)
which recovers the convergence rate for a continuous 2π-periodic function. Unfortunately, the condition, ![]() , is generally not true for an arbitrary function.
, is generally not true for an arbitrary function.
In recognizing this slow convergence problem, the subtraction of polynomials has been developed to remove the Gibbs phenomenon with ![]() (or its related derivatives) and to thus accelerate the convergence of resulting Fourier expansions [6] - [12] . In polynomial subtraction schemes, a new (or corrected) function
(or its related derivatives) and to thus accelerate the convergence of resulting Fourier expansions [6] - [12] . In polynomial subtraction schemes, a new (or corrected) function ![]() will be created with a desired smoothness through removing the potential jumps, such as, at the end points
will be created with a desired smoothness through removing the potential jumps, such as, at the end points
![]() (1.15)
(1.15)
where ![]() is a polynomial of degree 2K + 1, satisfying
is a polynomial of degree 2K + 1, satisfying
![]() (1.16)
(1.16)
The polynomials can be easily constructed, for example, using the Lanczos’s system of polynomials:
![]() , (1.17)
, (1.17)
![]() (1.18)
(1.18)
and
![]() (1.19)
(1.19)
Lanczos polynomials of even (odd) degrees are obviously even (odd) functions. It should be noted that Lanczos polynomials are closely related to Bernoulli polynomials which are also widely used in the methods of polynomial subtraction.
The first few Lanczos polynomials can be explicitly expressed as
![]() (1.20)
(1.20)
![]() (1.21)
(1.21)
![]() (1.22)
(1.22)
![]() . (1.23)
. (1.23)
For complete Fourier expansion of![]() ,
,
![]() . (1.24)
. (1.24)
For the sine expansion of![]() ,
,
![]() . (1.25)
. (1.25)
For the cosine expansion of![]() :
:
![]() . (1.26)
. (1.26)
Assume that ![]() is Cn−1 continuous on [−π, π] and its n-th derivative is absolutely integrable. Then the corrected function
is Cn−1 continuous on [−π, π] and its n-th derivative is absolutely integrable. Then the corrected function ![]() can be periodically extended into a 2π-periodic function of: a) CK continuity for K ≤ n − 1 in (1.12); b) C2K+1 continuity for 2K + 1 < n in (1.13) and c) C2K+2 continuity for 2K + 2 < n in (1.14).
can be periodically extended into a 2π-periodic function of: a) CK continuity for K ≤ n − 1 in (1.12); b) C2K+1 continuity for 2K + 1 < n in (1.13) and c) C2K+2 continuity for 2K + 2 < n in (1.14).
By recognizing the slower convergence of sine series than its cosine counterpart, a modified Fourier series was proposed as [1]
![]() (1.27)
(1.27)
If ![]() is differentiable and its derivative has bounded variation, the expansion coefficients, am and bm, in (1.15) will both decay like
is differentiable and its derivative has bounded variation, the expansion coefficients, am and bm, in (1.15) will both decay like ![]() [13] [14] , which is still considered relatively slow in many cases.
[13] [14] , which is still considered relatively slow in many cases.
2. An Alternative Form of Fourier Cosine Series
For a sufficiently smooth function ![]() defined on a compact interval [0, p], it can always be expanded into
defined on a compact interval [0, p], it can always be expanded into
![]() (2.1)
(2.1)
where
![]() . (2.2)
. (2.2)
It is known that expansion coefficients am decay like![]() .
.
To accelerate the convergence and maintain a close similarity to classical Fourier series, an alternative trigonometric expansion of ![]() is here sought in the form of
is here sought in the form of
![]() (2.3)
(2.3)
where
![]() (2.4)
(2.4)
and coefficients bp are to be determined as described below.
THEOREM 4. Let ![]() have Cn−1continuity on the interval [0, π] and its n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). If n ³ 2, then the Fourier coefficient am, as defined in (2.4), decays at a polynomial rate as
have Cn−1continuity on the interval [0, π] and its n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). If n ³ 2, then the Fourier coefficient am, as defined in (2.4), decays at a polynomial rate as
![]() (2.5)
(2.5)
provided that
![]() (2.6)
(2.6)
and
![]() (2.7)
(2.7)
Proof. By integrating by part, we have
![]() (2.8)
(2.8)
Denote![]() , then
, then
![]() (2.9)
(2.9)
for sufficiently large m.
Substracting (2.9) from (2.8) leads to
![]() (2.10)
(2.10)
The first two terms in (2.10) vanish if
![]() (2.11)
(2.11)
and
![]() (2.12)
(2.12)
In order to have a unique and smallest set of coefficients, bp, we set Q = P in (2.11) and (2.12), or equivalently, in (2.6) and (2.7). The convergence estimate, (2.5), becomes evident from (2.10) according to Theorem 2. W
Remark. If![]() , the relationship, (2.5), in Theorem 4 can be modified to
, the relationship, (2.5), in Theorem 4 can be modified to
![]() (2.13)
(2.13)
or, more explicitly,
![]() (2.14)
(2.14)
Alternatively, (2.4) can be expressed as
![]() (2.15)
(2.15)
where
![]() (2.16)
(2.16)
Equations (2.6) and (2.7) can be rewritten in matrix form as
![]() (2.17)
(2.17)
where
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
![]() (2.21)
(2.21)
![]() (2.22)
(2.22)
and
![]() (2.23)
(2.23)
in which
![]() (2.24)
(2.24)
and
![]() . (2.25)
. (2.25)
Determination of the coefficients, B1 and B2, involves the inversion of a Vandermonde-like matrix
![]() (2.26)
(2.26)
which is always invertable if xk ¹ xj for j ¹ k.
Consider a polynomial of degree 2P − 1
![]() . (2.27)
. (2.27)
Then it is obvious that
![]() (2.28)
(2.28)
where δij is Kronecker’s symbol.
According to (2.28), matrix C = [cik] is actually the inverse of matrix X.
To find an explicit expression for matrix C, let
![]() (2.29)
(2.29)
where
![]() (2.30)
(2.30)
and
![]() . (2.31)
. (2.31)
Thus, we have
![]() . (2.32)
. (2.32)
Comparing (2.32) with (2.27) leads to
![]() (2.33)
(2.33)
or
![]() . (2.34)
. (2.34)
In light of (2.34), the coefficients bp (![]() ) can be obtained as
) can be obtained as
![]()
![]() . (2.35)
. (2.35)
By making use of (2.21), the first few coefficients, for example, are readily found as:
![]() (2.36)
(2.36)
and
![]() (2.37)
(2.37)
for P=1;
![]() (2.38)
(2.38)
![]() (2.39)
(2.39)
![]() (2.40)
(2.40)
and
![]() (2.41)
(2.41)
for P = 2;
![]() (2.42)
(2.42)
![]() (2.43)
(2.43)
![]() (2.44)
(2.44)
![]() (2.45)
(2.45)
![]() (2.46)
(2.46)
and
![]() (2.47)
(2.47)
for P = 3.
EXAMPLE 1. Consider function![]() . Its conventional Fourier expansions are easily obtained as
. Its conventional Fourier expansions are easily obtained as
![]() (2.48)
(2.48)
or
![]() (2.49)
(2.49)
where
![]() (2.50)
(2.50)
Under the current framework, this function can be expanded as:
![]() (2.51)
(2.51)
where
![]() (2.52)
(2.52)
for P = 1;
![]() (2.53)
(2.53)
where
![]() (2.54)
(2.54)
for P = 2;
![]() (2.55)
(2.55)
where
![]() (2.56)
(2.56)
for P = 3.
A graphic display of the results, (2.48), (2.49), (2.51), (2.53) and (2.55), is given in Figure 1 for A = 4, B = 2, and C = 1. The corresponding truncation errors are plotted in Figure 2 and Figure 3.
![]()
Figure 1. Decays of expansion coefficients: bm in (2.48), am in (2.49), am in (2.51), am in (2.53), and am in (2.55).
3. An Alternative Form of Fourier Sine Series
Similarly, ![]() can also be expanded into sine series:
can also be expanded into sine series:
![]() (3.1)
(3.1)
where bp are the expansion coefficients to be determined, and
![]() . (3.2)
. (3.2)
THEOREM 5. Let ![]() have Cn−1 continuity on the interval [0, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Then for
have Cn−1 continuity on the interval [0, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Then for ![]() the Fourier coefficients of
the Fourier coefficients of ![]() defined in (3.1) decay at a polynomial rate as
defined in (3.1) decay at a polynomial rate as
![]() (3.3)
(3.3)
provided that
![]() (3.4)
(3.4)
and
![]() . (3.5)
. (3.5)
Proof. By integrating by part, we have
![]() (3.6)
(3.6)
The first two terms in (3.6) will both vanish if
![]() (3.7)
(3.7)
and
![]()
Figure 2. Truncation errors, ![]() , for the series expansions: (2.48), (2.49), (2.51), (2.53), and (2.55). M = 20.
, for the series expansions: (2.48), (2.49), (2.51), (2.53), and (2.55). M = 20.
![]()
Figure 3. Errors, ![]() , for series expansion (2.51): M = 10, M = 20 and M = 40.
, for series expansion (2.51): M = 10, M = 20 and M = 40.
![]() (3.8)
(3.8)
In order to have a unique and smallest set of coefficients, bp, we set Q = P in (3.7) and (3.8), or equivalently, in (3.4) and (3.5). The convergence estimate, (3.3), then becomes evident according to Theorem 2. W
Remark. If![]() , the relationship (3.3) can be modified to
, the relationship (3.3) can be modified to
![]() (3.9)
(3.9)
which can be further written in a shaper form as
![]() (3.10)
(3.10)
The expansion coefficients, am, can be alternatively expressed as
![]() (3.11)
(3.11)
where
![]() (3.12)
(3.12)
Actually,
![]() (see (2.16)). (3.13)
(see (2.16)). (3.13)
We can rewrite (3.4) and (3.5) in matrix form as
![]() (3.14)
(3.14)
where
![]() (3.15)
(3.15)
![]() (3.16)
(3.16)
![]() (3.17)
(3.17)
and
![]() . (3.18)
. (3.18)
Following the same procedures as described earlier, coefficients bp can be obtained from
![]() ,
,
![]() (3.19)
(3.19)
Using this formula, the first several coefficients are easily determined as:
![]() (3.20)
(3.20)
and
![]() (3.21)
(3.21)
for P = 1;
![]() (3.22)
(3.22)
![]() (3.23)
(3.23)
![]() (3.24)
(3.24)
and
![]() (3.25)
(3.25)
for P = 2;
![]() (3.26)
(3.26)
![]() (3.27)
(3.27)
![]() (3.28)
(3.28)
![]() (3.29)
(3.29)
![]() (3.30)
(3.30)
and
![]() (3.31)
(3.31)
for P = 3.
EXAMPLE 2. Consider function![]() . The classical sine series expansion of this function is easily found as
. The classical sine series expansion of this function is easily found as
![]() (3.32)
(3.32)
where
![]() (3.33)
(3.33)
In the context of the current framework, this function can be expressed as
![]() (3.34)
(3.34)
where
![]() (3.35)
(3.35)
for P = 1;
![]() (3.36)
(3.36)
where
![]() (3.37)
(3.37)
for P = 2.
4. An Alternative Form of Fourier Series Expansion
Let ![]() be defined on the interval [−π, π]. It can also be expanded into a complete trigonometric series as
be defined on the interval [−π, π]. It can also be expanded into a complete trigonometric series as
![]() (4.1)
(4.1)
where am and bm are the expansion coefficients to be calculated from
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
and ![]() and
and ![]() are to be determined as follows.
are to be determined as follows.
THEOREM 6. Let ![]() have Cn−1 continuity on the interval [−π, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Then the Fourier coefficients of
have Cn−1 continuity on the interval [−π, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Then the Fourier coefficients of![]() , as defined in (4.2)and (4.3), decay at a polynomial rate as
, as defined in (4.2)and (4.3), decay at a polynomial rate as
![]() (4.4)
(4.4)
and
![]() (4.5)
(4.5)
provided that
![]() (4.6)
(4.6)
![]() (4.7)
(4.7)
![]() (4.8)
(4.8)
and
![]() . (4.9)
. (4.9)
Proof. Function ![]() can be considered as the superposition of an even function
can be considered as the superposition of an even function![]() and an odd function
and an odd function![]() . Theorems 4 is then directly applicable to g(x) on [0, π]. Thus, (4.4) holds if
. Theorems 4 is then directly applicable to g(x) on [0, π]. Thus, (4.4) holds if
![]() (4.10)
(4.10)
and
![]() . (4.11)
. (4.11)
Since
![]() (4.12)
(4.12)
and
![]() , (4.13)
, (4.13)
(4.10) and (4.11) can be rewritten as (4.6) and (4.7), respectively.
Similarly, relationship (4.5) is readily obtained from applying Theorem 5 to the odd function h(x) on interval [0, π] by recognizing that
![]() (4.14)
(4.14)
and
![]() . (4.15)
. (4.15)
The expansion coefficients of g(x) are determined from
![]() (4.16)
(4.16)
Similarly, the expansion coefficients of h(x) are determined from
![]() (4.17)
(4.17)
The even (odd) extension of ![]() (
(![]() ) onto [−π, 0) will lead to an even (odd) function
) onto [−π, 0) will lead to an even (odd) function ![]()
(![]() )on [−π, π]. Expression (4.1) will then become evident. W
)on [−π, π]. Expression (4.1) will then become evident. W
Alternatively, (4.2) and (4.3) can be expressed as
![]() (4.18)
(4.18)
and
![]() (4.19)
(4.19)
where ![]() is given in (2.16).
is given in (2.16).
The coefficients ![]() and
and ![]() are readily calculated from (2.35) and (3.19), respectively, by letting
are readily calculated from (2.35) and (3.19), respectively, by letting
![]() (4.20)
(4.20)
and
![]() (4.21)
(4.21)
EXAMPLE 3. Consider function![]() . Its classical Fourier expansion is easily found as
. Its classical Fourier expansion is easily found as
![]() . (4.22)
. (4.22)
By setting P = 0 and Q = 1 in (4.1), we have
![]() (4.23)
(4.23)
and
![]() (4.24)
(4.24)
where
![]() (4.25)
(4.25)
It is seen from (4.25) that the sine series now converges at a rate of m−3 which is faster than m2 for its cosine counterpart. If desired, the convergence of the series expansion in the form of (4.1) can be further accelerated by setting P = Q = 1. Accordingly, in addition to (4.23), we have
![]() (4.26)
(4.26)
and
![]() (4.27)
(4.27)
where
![]() (4.28)
(4.28)
The series expansion given in (4.27) will converge at a rate of m−3 in comparison with m−2 for that in (4.24).
5. Corollaries
COROLLARY 1. Let ![]() have Cn−1continuity on the interval [0, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Assume n ³ 2. Then
have Cn−1continuity on the interval [0, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Assume n ³ 2. Then ![]() can be expanded as
can be expanded as
![]() (5.1)
(5.1)
and
![]() (5.2)
(5.2)
Provided that
![]() (5.3)
(5.3)
and
![]() (5.4)
(5.4)
where ![]() and
and ![]() are calculated from(2.4) and (2.35), respectively.
are calculated from(2.4) and (2.35), respectively.
Proof. For![]() , denote
, denote
![]() (5.5)
(5.5)
and
![]() (5.6)
(5.6)
or, alternatively, (5.3) and (5.4).
Then expansion (5.1) follows immediately from (2.3) in view that
![]()
Since ![]() for
for![]() , (5.2) is evident from (2.5). W
, (5.2) is evident from (2.5). W
COROLLARY 2. Let ![]() have Cn−1 continuity on the interval [0, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Then for
have Cn−1 continuity on the interval [0, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points). Then for![]() ,
, ![]() can be expanded as
can be expanded as
![]() (5.7)
(5.7)
and
![]() (5.8)
(5.8)
provided that Am and ![]() satisfy (5.3) and (5.4), and
satisfy (5.3) and (5.4), and ![]() and
and ![]() are calculated from (3.2) and (3.19), respectively.
are calculated from (3.2) and (3.19), respectively.
Proof. By (5.5) and (5.6), we have
![]() (5.9)
(5.9)
Thus, (5.7) and (5.8) become obvious from (3.1) and (3.3), respectively. W
COROLLARY 3. Let ![]() have Cn−1 continuity on the interval [−π, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points. Then for
have Cn−1 continuity on the interval [−π, π] and the n-th derivative is absolutely integrable (the n-th derivative may not exist at certain points. Then for ![]() and
and![]() ,
, ![]() can be expanded as
can be expanded as
![]() (5.10)
(5.10)
and
![]() (5.11)
(5.11)
and
![]() (5.12)
(5.12)
provided that
![]() (5.13)
(5.13)
![]() (5.14)
(5.14)
![]() (5.15)
(5.15)
and
![]() (5.16)
(5.16)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are defined in the same way as those in (4.1).
are defined in the same way as those in (4.1).
Since Corollary 3 is obvious from Theorem 6 and Corollaries 1 and 2, its proof will not be given here.
Notice that in (5.1)
![]() (5.17)
(5.17)
where
![]() (5.18)
(5.18)
and ![]() (superposed * indicates taking complex conjugate).
(superposed * indicates taking complex conjugate).
Remark. In Corollary 1, (5.1) can be alternatively written as
![]() (5.19)
(5.19)
where
![]() (5.20)
(5.20)
and![]() .
.
Similarly, (5.7) in Corollary 2 can be written as
![]() (5.21)
(5.21)
where
![]() (5.22)
(5.22)
and![]() .
.
And (5.9) in Corollary 3 as
![]() (5.24)
(5.24)
where
![]() (5.25)
(5.25)
and![]() .
.
6. Conclusion
Alternative Fourier series expansions have been presented in an effort of better representing a sufficiently smooth function in a compact interval. The series expansions can take various forms, resulting in different rates of convergence. When one of the series expansions, for example, is used to solve a boundary value problem, its convergence rate needs to be compatible with the smoothness of the solution “physically” dictated by the problem. Thus, there may exist the best form for any given problem. Among other important applications, the new Fourier series will potentially lead to a new path for solving differential equations and boundary value problems.