1. Introduction
Two millenaries ago, Thales discovered the electrical properties of amber (
, elektron) and the magnetic properties of magnetite (from mount Magnetos) quantified by Coulomb [1] and Poisson [2] . In 1924, Bieler [3] made an unsuccessful attempt to explain with an attractive magnetic inverse fourth-power term in the law of force, unfortunately with the wrong sign. Indeed, it needs only to reuse the Rutherford formula where −2 electric is replaced by −6 magnetic [4] .
The neutron, discovered in 1931 by Chadwick, seeming to be uncharged, the electromagnetic hypothesis of the nuclear interaction was abandoned. The magnetic moments of the proton and of the deuteron were discovered in 1932 by Stern [5] and the magnetic moment of the neutron in 1938 by Bloch [6] . Assuming the additivity of the magnetic moments, he found that, in the deuteron, the magnetic moment of the neutron was opposite to that of the proton. The existence of a magnetic moment in the neutron proved the existence of electric charges and currents in the neutron, indicating that it is not an elementary particle, as it carries no net charge but still interacts with a magnetic field [6] .
In nuclear physics, electric (except so-called Coulomb force) and magnetic interactions between nucleons are still considered to be negligible, although: “The positive charge attracts negative charges to the side closer to itself and leaves positive charges on the surface of the far side. The attraction by the negative charges exceeds the repulsion from the positive charges, there is a net attraction” [7] . Indeed, a proton attracts a neutron as a rubbed plastic pen attracts small pieces of paper.
The electrostatic attraction in the deuteron between a proton and a not so neutral neutron is equilibrated statically by the repulsion between the opposite magnetic moments of the proton and of the neutron. The magnetic interaction between nucleons is attractive or repulsive depending on the position and orientation of their magnetic moments. First theoretical results have been obtained for hydrogen and helium isotopes [8] [9] . The results shown in this paper are for the deuteron and the α particle.
2. Electromagnetic Potential Energy
The sum of the electric and magnetic potential energies between electromagnetic particles is the fundamental combination of Coulomb electric and Poisson magnetic potentials [10] - [12] :
(1)
The first term is the sum of the electrostatic interaction potential energy between electric charges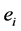 
and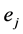 
separated by
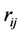. The second term is the magnetic interaction potential energy between magnetic moments 
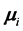and
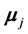, separated by
.
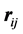3. Deuteron Electromagnetic Potential Energy
3.1. Deuteron Electrostatic Potential Energy per Nucleon (Coulomb)
The electrostatic potential energy per nucleon 
of this system of the three point charges of the deuteron is, from formula (1), where A is the atomic number:
(2)
, 
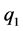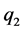and 
are the three electrostatic charges.
, 
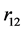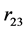and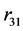 
are their separation distances along their common axis. The total electrostatic potential energy between the 3 electric charges of the deuteron (Equation (2)) becomes fundamental, except for a, adjusted to obtain a horizontal inflection point, replacing a real minimum (
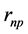and a are defined on Figure 1). The electric potential, being negative, is attractive:
![]()
(3)
3.2. Deuteron Magnetic Potential Energy per Nucleon (Poisson)
According to the general formula (1) the total magnetic potential energy of the deuteron is:
![]()
(4)
The magnetic moments of the proton and of the neutron in the deuteron are known to be collinear and opposite, (![]()
and![]()
), as shown on Figure 1. The coefficient in the brackets above being equal to![]()
, the magnetic potential is positive, repulsive:
![]()
(5)
3.3. Deuteron Electromagnetic Potential Energy per Nucleon
Adding the attractive electrostatic Equation (3) and the repulsive magnetic Equation (5), the electromagnetic potential formula (1) becomes, per nucleon, with A = 2 of the deuteron 2H:
![]()
(6)
or, numerically (see Appendix):
![]()
(7)
There is one variable ![]()
and one parameter a in formula (7). In order to find the binding energy it is necessary to adjust the parameter a of the curve to obtain a potential minimum (in fact, a local minimum, a horizontal inflection point) for both ![]()
and a. This is not to be confused with fitting to adjust the binding energy. A real minimum [13] would be better, of course, but, needing an empirical parameter, would break the fundamental nature of the theory. The horizontal inflection part of the curve corresponds to the deuteron binding energy. The result, obtained by applying electrostatic Coulomb’s law and magnetic Poisson’s law with the corresponding fundamental constants, is in compliance with the experimental value of the deuteron binding energy per nucleon −1.11 MeV (Figure 1). There is only one horizontal inflection point per nucleus, adjusted manually by trial and error (Figure 2). It coincides, as by chance, with the binding energy of the nucleus.
4. Alpha Particle Electromagnetic Energy per Nucleon
4.1. Interactions between Neutrons and between Protons
The single neutron-neutron and proton-proton bonds, being small in comparison with the 4 neutron-proton bonds, have been neglected provisionally. The electric interactions between protons are surely repulsive. The electric interaction between neutrons is probably weak. The magnetic interactions between neutrons and between protons are assumed to be repulsive. The structure of 4He is shown on Figure 3. The graphical solution (Figure 2) gives, for the α particle, a binding energy per nucleon of −7.6 MeV, stronger than the experimental value, −7.07 MeV, by 10 per cent, due probably to the neglect, in a first approximation of the magnetic repulsion between neutrons and between protons. More precise results should be obtained by taking into account these interactions.
4.2. Proton-Neutron Interactions Only, Provisionally
We shall calculate the 4He binding energy per nucleon from the deuteron 2H potential energy, which is, as seen before (Equation (6)):
![]()
(8)
A neutron-proton 4He bond is one total attractive 2H deuteron bond, thus −2.2 MeV equilibrated by the product of 2 magnetic interactions, inclined by 60˚, thus dividing the repulsive magnetic potential binding energy twice by 2 thus by 4. The magnetic moments of the proton and the neutron, being perpendicular (Figure 3), according to formula (1), the Poisson formula has a coefficient of 3 instead of 2 for the deuteron. The potential energy per nucleon is thus:
![]()
(9)
or, numerically (see Appendix):
![]()
Figure 2. The binding energies per nucleon of 2H and 4He are calculated with Coulomb, electric, and Poisson, magnetic, fundamental laws, without phenomenological parameters. It can be seen that the so-called Coulomb singularity is not a real problem: it just need to replace the minimum by a horizontal inflection point, the radius of the elementary electric charges being unknown, assumed to be point-like. The binding energy is calculated graphically as −1.2 for an experimental value of −1.1 for 2H and −7.6 MeV for an experimental value of −7.1 MeV for 4He.
![]()
Figure 3. The deuteron 2H has one neutron-proton bond, as shown on Figure 1, thus a total binding energy of −2.2 MeV. 4He has 4 deuteron bonds, inclined at 60˚, thus multiplying twice by 4 the total 2H binding energy, giving an approximate total binding energy of ![]()
somewhat larger than the experimental value, −28 MeV. The difference is probably due to the repulsive neutron-neutron and proton-proton potentials, not taken into account.
![]()
(10)
The graphical solution (Figure 2) gives, for the α particle, a binding energy of −7.6 MeV, stronger than the experimental value, −7.07 MeV, too large by 10 per cent, due probably to the magnetic repulsion between neutrons and between protons, neglected in a first approximation. More precise results should be obtained by taking into account these interactions.
5. Conclusions
The binding energies of the deuteron and of the α particle have been calculated by applying only fundamental electromagnetic laws and constants with the experimentally proved properties of the nucleons and the nuclei. The binding energy error is about a few percent for the deuteron and almost 10 percent for the α particle, due to the neglect of the neutron-neutron and proton-proton interactions. The only adjusted parameter a is used to obtain the single horizontal inflection point characterizing the binding energy of a nucleus. Not to be confused with fits.
The agreement between experimental results and the electromagnetically calculated Rutherford nuclear scattering (normal and not so “anomalous”) and nuclear binding energy proves the electromagnetic nature of the nuclear interaction. No need of hypothetical strong force and quarks.
Acknowledgements
Thanks to persons at Dubna for their interest to my electromagnetic theory of the nuclear energy. The first question was about scattering. I said I don’t know. Now I know: The anomalous Rutherford scattering is magnetic. The second question was: “The strong force doesn’t exist?” and a third one about orbiting nucleons [14] .
Appendix: Fundamental Constants Used (CODATA)
・ Light velocity:
![]()
・ Fundamental Electric charge
![]()
(11)
・ Electric constant
![]()
(12)
・ Magnetic constant
![]()
(13)
・ Proton mass:
![]()
(14)
・ Proton magnetic moment
![]()
(15)
・ Neutron magnetic moment
![]()
(16)
・ Proton-neutron magnetic moments combined
![]()
(17)