Stability Analysis of Bubonic Plague Model with the Causing Pathogen Yersinia pestis in the Environment ()
Received 23 June 2016; accepted 13 September 2016; published 16 September 2016

1. Introduction
Bubonic plague is the bacterial infection caused by Yersinia pestis when the bacteria infect lymphatic system [1] . It is characterised by geographical foci and extraordinarily adaptation capability which gives it ability to re- emerge even after decades of silence. Thus even though the disease is historic it still infect and kill thousands of people around the world [2] .
The disease mainly affects wild rodents, it can also be transmitted to human and other domestic animals through flea bites. Bubonic plague causes fever and very throbbing swelling of the lymph glands also called buboes, which is the reason why the disease is called bubonic plague.
When the flea is infested with pathogens causing bubonic plague the bacteria multiply in the proventriculus (foregut) of the flea [3] . The bacteria have the tendency of blocking the flea’s bloodsucking apparatus which consequently lead to inability of flea to pump blood into the midgut for digestion. This makes the flea to become ravenous as a result flea bites the host repetitively while vomiting the bacteria causing disease into the host. When a host dies, fleas move off the body to seek another live warm-blooded host [4] .
Although it is not yet clearly known how, but Yersinia pestis may survive in the soil and remain viable and fully virulent for 40 weeks in soil and can cause the infection upon the adequate interaction with the susceptible individual. This is believed to be the reason for possible mechanism of interepizootic persistence, epizootic spread, and as a factor defining plague foci [5] .
In this paper, we discuss the stability analysis of the bubonic plague epidemic model in human, rodent and flea population. The model includes the transmission from the environment to the susceptible human or rodent. We also discuss the disease-free equilibrium point, endemic equilibrium point of the model and analyze the local and global stability of these steady states. We finally use the numerical simulation to support our analytical results.
2. Model Formulation
This paper presents the stability analysis of the bubonic plague epidemic model developed by [6] . The model includes four interacting population which are: human population, Flea population, Rodent population and pathogens in the environment is developed. We use ,
, 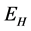 ,
, 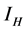 and
and 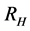 to represent Susceptible human beings, Exposed human beings, Infected human beings and Recovered human beings respectively;
to represent Susceptible human beings, Exposed human beings, Infected human beings and Recovered human beings respectively;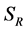 ,
, 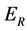 and
and 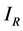 for Susceptible rodents, Exposed rodents and Infected rodents respectively. The Susceptible and the Infectious flea are denoted by
for Susceptible rodents, Exposed rodents and Infected rodents respectively. The Susceptible and the Infectious flea are denoted by 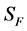 and
and 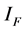 respectively. The pathogens in the environment are denoted by A. The total population for human being, rodent and flea population is by
respectively. The pathogens in the environment are denoted by A. The total population for human being, rodent and flea population is by
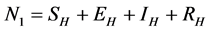 (1a)
(1a)
 (1b)
(1b)
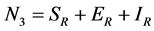 (1c)
(1c)
The parameters used in the model are described in Table 1.
Model Equations for Bubonic Plague
Since we allow the population in and out of the compartments, the rate at which new infections occur in a population will depend on the fraction of the population that is infected (disease prevalence). The infection rate in human depends on the probability that a contact between infectious flea and susceptible human and between infectious environment and susceptible human leads to infection. For the rodent the infection depends on the probability that a contact between infectious flea and susceptible rodent and between infectious environment and susceptible rodent leads to infection. For the flea the infection depends on the probability that a contact between infectious human and susceptible flea and between infectious rodent and susceptible flea leads to infection. Therefore the infection rates of susceptible humans, rodent population and flea population are as given in (2a), (2b) and (2c) respectively.
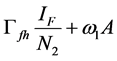 (2a)
(2a)
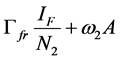 (2b)
(2b)
![]()
Table 1. Parameters and their description.
![]() (2c)
(2c)
Pathogens in the environment are recruited at a constant rate ![]() and they are removed through natural death
and they are removed through natural death ![]() or removed when they contact with susceptible human and rodent at the rates
or removed when they contact with susceptible human and rodent at the rates ![]() and
and ![]() respectively.
respectively.
Using the definition of variables and parameters stated in Table 1, we drive model for the dynamics of bubonic plague disease in human, rodent, flea and pathogens in the environment as given in (3), (4), (5) and (6) respectively.
Human
![]() (3a)
(3a)
![]() (3b)
(3b)
![]() (3c)
(3c)
![]() (3d)
(3d)
Rodent
![]() (4a)
(4a)
![]() (4b)
(4b)
![]() (4c)
(4c)
Flea
![]() (5a)
(5a)
![]() (5b)
(5b)
where ![]()
Pathogens
![]() (6)
(6)
3. Steady State and Local Stability of the Critical Points
In this section we consider existence of equilibrium states and stability of the equilibrium states of the system (3)-(6).
3.1. Disease Free Equilibrium
The model has disease free equilibrium which is obtained by setting![]() ,
, ![]() ,
, ![]() and
and ![]() and the derivatives equal to zero into the system (3)-(6).
and the derivatives equal to zero into the system (3)-(6).
Then we have the disease free-equilibrium point given as![]() ,
, ![]() ,
, ![]() and
and ![]() for Human, Rodent, Flea and Pathogen respectively.
for Human, Rodent, Flea and Pathogen respectively.
Then the disease free equilibrium of the entire system is
![]()
3.2. Local Stability of the Disease-Free Equilibrium Point
In this section we consider the local stability analysis of the disease free equilibrium point of the bubonic plague disease system (3)-(6). We analyze the local stability of the disease free equilibrium point using the Jacobian method in which all equations in system (3)-(6) are considered and analyzed at the disease free equilibrium![]() . In this method we compute and examine the eigenvalues of Jacobian matrix of the system (3)-(6) to prove that the DFE is locally and asymptotically stable. We are required to show that all real parts of the eigenvalues at
. In this method we compute and examine the eigenvalues of Jacobian matrix of the system (3)-(6) to prove that the DFE is locally and asymptotically stable. We are required to show that all real parts of the eigenvalues at ![]() are negative. Now in order to attest that the eigenvalues are negative we need to prove the general condition that the determinant and the trace of the Jacobian matrix are positive and negative respectively [7] .
are negative. Now in order to attest that the eigenvalues are negative we need to prove the general condition that the determinant and the trace of the Jacobian matrix are positive and negative respectively [7] .
Now the Jacobian matrix of the system (3)-(6) at ![]() is given by:
is given by:
![]() (7)
(7)
where
![]()
We now use Trace and determinant method to check the stability of the disease free equilibrium point ![]() in which we need to prove that the trace and the determinant of matrix (7) are negative and positive respectively
in which we need to prove that the trace and the determinant of matrix (7) are negative and positive respectively
Then using mathematica software we prove that trace of the matrix (7) given by
![]()
where
![]()
It is clear that the trace of the matrix (7) in negative. Then using the same software (mathematica) we are able to prove that the determinant of the matrix (7) is positive provided:
![]()
where
![]() (8)
(8)
is the basic reproduction number,![]() .
.
![]() measures the average number of secondary infection produced when a typical infectious individual enters an entirely susceptible population. In our case, due to presence of multiple transmission cycle the basic reproductive number do not give the number of cases infected by a single individual but rather the geometric mean of the number of infections per generation [8] .
measures the average number of secondary infection produced when a typical infectious individual enters an entirely susceptible population. In our case, due to presence of multiple transmission cycle the basic reproductive number do not give the number of cases infected by a single individual but rather the geometric mean of the number of infections per generation [8] .
Referring to (8), the geometric mean of the number of infections per generation depends on: rodent’s infective
period![]() , the probability that flea gets the disease from the rodent or human which are
, the probability that flea gets the disease from the rodent or human which are ![]() or
or ![]() respectively The human infective period
respectively The human infective period![]() , probability that human survive the infected class
, probability that human survive the infected class![]() , the rate at which fleas gets infected
, the rate at which fleas gets infected![]() , flea’s infective period
, flea’s infective period![]() , probability that rodent survive the infected class
, probability that rodent survive the infected class![]() , the adequate contact rate flea to human
, the adequate contact rate flea to human![]() , the adequate contact rate flea to
, the adequate contact rate flea to
rodent ![]() and the rate at which human and rodent become exposed to the the disease which are
and the rate at which human and rodent become exposed to the the disease which are ![]() and
and ![]() respectively.
respectively.
Thus disease free equilibrium point ![]() is therefore locally asymptotically stable and leads to the following theorem:
is therefore locally asymptotically stable and leads to the following theorem:
Theorem 1. The Disease Free Equilibrium ![]() of bubonic plague is locally asymptotically stable if
of bubonic plague is locally asymptotically stable if ![]() and unstable if
and unstable if![]() .
.
3.3. Global Stability of the Disease-Free Equilibrium Point
In this section we analyze the global stability of the disease free equilibrium point using Metzler matrix method as stated by [9] . To do this we first sub-divide the general system (3)-(6) of bubonic plague disease into transmitting and non-transmitting component.
Now let ![]() be the vector for non-transmitting compartment,
be the vector for non-transmitting compartment, ![]() be the vector for transmitting compartment and
be the vector for transmitting compartment and ![]() be the vector of disease free point. Then
be the vector of disease free point. Then
![]() (9)
(9)
We then have
![]()
![]()
Now to prove the global stability of the DFE we need to show that Matrix ![]() has real negative eigenvalues and
has real negative eigenvalues and ![]() is a Metzler matrix in which all off diagonal element must be non-negative. Referring to (9) we write the general model as given below
is a Metzler matrix in which all off diagonal element must be non-negative. Referring to (9) we write the general model as given below
![]()
and
![]()
For
![]()
Now using the transmitting and non-transmitting element on the general system we will have the matrices below:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
where![]() ,
, ![]() and
and ![]()
Now when we consider matrix![]() , the computation shows that the eigenvalues are real and negative, which now confirms that the system
, the computation shows that the eigenvalues are real and negative, which now confirms that the system
![]()
is globally and asymptotically stable at![]() . And for matrix
. And for matrix ![]() we find that all its off-diagonal elements are non-negative and thus
we find that all its off-diagonal elements are non-negative and thus ![]() is a Metzler stable matrix.Therefore Disease Free Equilibrium point for the general bubonic plague system is globally asymptotically stable as a result we have the following theorem:
is a Metzler stable matrix.Therefore Disease Free Equilibrium point for the general bubonic plague system is globally asymptotically stable as a result we have the following theorem:
Theorem 2. The disease-free equilibrium point is globally asymptotically stable in ![]() if
if ![]() and un- stable if
and un- stable if![]() .
.
3.4. Existence of Endemic Equilibrium
Here we consider the situation in which the disease persist in a population. We investigate conditions for existence of the endemic equilibrium point of the system (3)-(6). The endemic equilibrium point ![]() is obtained by solving the equations obtained by setting the derivatives of (3)-(6) equal to zero as in (13)-(16) which exist for
is obtained by solving the equations obtained by setting the derivatives of (3)-(6) equal to zero as in (13)-(16) which exist for![]() .
.
Human
![]() (13a)
(13a)
![]() (13b)
(13b)
![]() (13c)
(13c)
![]() (13d)
(13d)
Rodent
![]() (14a)
(14a)
![]() (14b)
(14b)
![]() (14c)
(14c)
Flea
![]() (15a)
(15a)
![]() (15b)
(15b)
where ![]()
Pathogens
![]() (16)
(16)
Since it is difficult to obtain explicitly the endemic equilibrium points of the model we will prove its existence using the study by [10] [11] . For the endemic equilibrium to exist it must satisfy the condition ![]() or
or ![]() or
or ![]() or
or ![]() or
or ![]() or
or ![]() that is
that is ![]() or
or ![]() or
or ![]() or
or ![]() or
or ![]() or
or ![]() or
or ![]() or
or ![]() or
or ![]() must be satisfied. Now adding system (13)-(16) we have
must be satisfied. Now adding system (13)-(16) we have
![]() (17)
(17)
Substituting![]() ,
, ![]() and
and ![]() in (17) we have
in (17) we have
![]() (18)
(18)
But from Equation (16), we have ![]()
It follows that
![]()
Since![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() we can discern that
we can discern that![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() implying that
implying that![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Hence endemic equilibrium point of the bubonic plague disease model in human, rodent, flea and pathogens in the environment exists.
Since the endemic equilibrium points exist, we now determine the conditions under which they are stable or unstable. We prove whether the solution starting sufficiently close to the equilibrium remains close to the equilibrium and approaches the equilibrium as![]() , or if there are solutions starting arbitrary close to the equilibrium which do not approach it respectively.
, or if there are solutions starting arbitrary close to the equilibrium which do not approach it respectively.
3.5. Global Stability of Endemic Equilibrium Point
Using the idea from the study by [12] we say that the local stability of the Disease Free Equilibrium advocates for local stability of the Endemic Equilibrium for the reverse condition. We then work to find the global stability of Endemic equilibrium using a Korobeinikov approach as stipulated in [12] - [14] by forming a suitable Lyapunov function for our general model as given below:
We construct the Lyapunov function as given in the form:
![]()
where ![]() is defined as a properly selected positive constant,
is defined as a properly selected positive constant, ![]() defines the population of the
defines the population of the ![]() compartment, and
compartment, and ![]() is the equilibrium point.
is the equilibrium point.
We will have the following Lyapunov function,
![]()
The constants ![]() are non negative in
are non negative in ![]() such that
such that ![]() for
for![]() . The Lyapunov function V together with its constants
. The Lyapunov function V together with its constants ![]() chosen in such way that V is continuous and differentiable in a space
chosen in such way that V is continuous and differentiable in a space
We then compute the time derivative of V from it we get;
![]()
Now using the general system (3)-(6) we will have
![]()
At endemic equilibrium point we have
Human
![]() (19a)
(19a)
![]() (19b)
(19b)
![]() (19c)
(19c)
![]() (19d)
(19d)
Rodent
![]() (20a)
(20a)
![]() (20b)
(20b)
![]() (20c)
(20c)
Flea
![]() (21a)
(21a)
![]() (21b)
(21b)
where ![]()
Pathogens
![]() (22)
(22)
We can then rewrite ![]() using (19), (20), (21) and (22) as:
using (19), (20), (21) and (22) as:
![]()
After simplification the above equation becomes:
![]()
where the function ![]() is non positive, Now following the procedures by [15] [16] . We have
is non positive, Now following the procedures by [15] [16] . We have ![]() for all
for all![]() ,
,
Then ![]() for all
for all ![]() and it is zero when
and it is zero when![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() Hence the largest compact invariant set
Hence the largest compact invariant set
in ![]() such that
such that ![]() is the singleton
is the singleton ![]() which is Endemic Equilibrium
which is Endemic Equilibrium
point of the model system (3)-(6).
LaSalles’s invariant principle by [17] then implies that ![]() is globally asymptotically stable in the interior of the region of
is globally asymptotically stable in the interior of the region of ![]() and thus leads to the Theorem 3.
and thus leads to the Theorem 3.
Theorem 3. If ![]() then the bubonic plague disease model system (3)-(6) has a unique endemic equili- brium point
then the bubonic plague disease model system (3)-(6) has a unique endemic equili- brium point ![]() which is globally asymptotically stable in
which is globally asymptotically stable in ![]()
4. Numerical Simulation
Numerical simulation is carried out in order to observe and understand the kinetics of bubonic plague disease and demonstrate analytical results. In particular we illustrate through numerical simulation the stability of the endemic equilibrium states in human, rodent, flea and pathogens in the environment.
Parameter Values
The values of the parameters used in bubonic plague disease model are shown in Table 2. The parameters are taken from the previous studies that relate to this study, existing information and through estimation.
In the simulation we assume different cases where each sub-population starts at different initial values (six different initial values) ultimately returns to its endemic point. We thus justify that a solution that starts sufficiently close to the equilibrium remains close to it and it eventually approaches the equilibrium as![]() .
.
Figure 1 shows the dynamical behavior of the human population. The sub-Figure 1(a) shows a marginal increase in number of susceptible human as people moves in through migration. When the disease becomes endemic, the number of susceptible human decreases as they becomes exposed to the disease due to the increase of force of infection which resembles to the general scenario of vector borne infection as depicted in [23] . Given that the model assumes no treatment nor vaccination is applied, it thus justifies the behavior illustrated in sub-Figure 1(b). The figure shows the very slight increase of a exposed human beings before it drops to its endemic level as the large number of exposed human progresses and become infected human. The increase of number of infected human beings from the exposed class is depicted in sub-Figure 1(c). We can see that in the first five years the number infected human subgroup experience a substantial increase before it decreases to its endemic level. The decrease in number of infected human is mainly through natural death and disease induced death whereas very few will recover and join a recovery class. The system considers only natural recovery (recovery due to individual’s strong body immunity), thus the number of recovery human will slightly increase before it decreases and reaches its endemic level as illustrated in sub-Figure 1(d) [24] [25] .
![]()
Table 2. Parameters values for Bubonic Plague disease model.
Figure 2 shows the dynamics in rodent population. The results seen in this figure also settles with the findings by [26] [27] . We can see from sub-Figure 2(a) that the susceptible rodent population drops very fast within the first year, before it slightly rise due to migration at the rate![]() , to its endemic equilibrium level. The quick drop of susceptible rodent may be due to the fact that rodents are the primary victim of bubonic plague so that when the disease is endemic most of them are infected and become exposed to the disease [28] . The increase of the rate of infection in susceptible rodent population proportionally increase the number of exposed rodent [29] . After the significant increase of the exposed rodent population within the first five years it then drops to its endemic level. It takes only 2 to 6 days for an exposed rodent to become infectious [30] which is the reason for a quick decrease of exposed rodent as seen in sub-Figure 2(b). The infectious rodent population increases as the number of rodent progressing from exposed class to infectious increase.
, to its endemic equilibrium level. The quick drop of susceptible rodent may be due to the fact that rodents are the primary victim of bubonic plague so that when the disease is endemic most of them are infected and become exposed to the disease [28] . The increase of the rate of infection in susceptible rodent population proportionally increase the number of exposed rodent [29] . After the significant increase of the exposed rodent population within the first five years it then drops to its endemic level. It takes only 2 to 6 days for an exposed rodent to become infectious [30] which is the reason for a quick decrease of exposed rodent as seen in sub-Figure 2(b). The infectious rodent population increases as the number of rodent progressing from exposed class to infectious increase. ![]() then drops to its endemic level as it experience both natural and disease induced death as in sub-Figure 2(c).
then drops to its endemic level as it experience both natural and disease induced death as in sub-Figure 2(c).
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 2. Simulation of the model’s solution trajectories to show stability of the endemic point in subsystem (4).
The dynamics in the flea population are as seen in Figure 3, we can see that the number of susceptible flea decreases exponentially as they die naturally or acquire infection from the infected rodent or human at the rate ![]() or
or ![]() respectively see sub-Figure 3(a). The increased death of rodent due to the endemicity of the disease, will as a result lead to scarcity of hosts for flea to feed on and thus die [26] . The addition of natural and disease induced death in infected flea population will lead to a quick drops to its endemic level as illustrated in sub-Figure 3(b) (this corresponds well with the findings in the study by [20] [31] ). The pathogens in the environment are removed when they come to contact with the susceptible human and rodent at the rate
respectively see sub-Figure 3(a). The increased death of rodent due to the endemicity of the disease, will as a result lead to scarcity of hosts for flea to feed on and thus die [26] . The addition of natural and disease induced death in infected flea population will lead to a quick drops to its endemic level as illustrated in sub-Figure 3(b) (this corresponds well with the findings in the study by [20] [31] ). The pathogens in the environment are removed when they come to contact with the susceptible human and rodent at the rate ![]() and
and ![]() respectively and due to natural death at the rate
respectively and due to natural death at the rate![]() . Since we assume that human and rodent infectious classes have a negligible contribution in increasing the number of pathogens in the environment (see Equation (6)). Now as the disease become endemic the rates
. Since we assume that human and rodent infectious classes have a negligible contribution in increasing the number of pathogens in the environment (see Equation (6)). Now as the disease become endemic the rates ![]() and
and ![]() increase which in turn decrease the number of pathogens in the environment. Pathogens are also highly affected by the condition in the environment (temperature, humidity and precipitation). Most of the time this lead to a massive decay of the pathogens population in the environment as the environment is not favorable for their survival and growth [32] Then the number of pathogens in the environment will gradually decrease to its endemic level as in Figure 4.
increase which in turn decrease the number of pathogens in the environment. Pathogens are also highly affected by the condition in the environment (temperature, humidity and precipitation). Most of the time this lead to a massive decay of the pathogens population in the environment as the environment is not favorable for their survival and growth [32] Then the number of pathogens in the environment will gradually decrease to its endemic level as in Figure 4.
![]() (a)
(a)![]() (b)
(b)
Figure 3. Simulation of the model’s solution trajectories to show stability of the endemic point of subsystem (5).
![]()
Figure 4. Simulation of the model’s solution trajectories to show stability of the endemic point in (6).
5. Conclusion
In this paper, we have considered a bubonic plague in human, rodent and flea with Yersinia pestis in the environment. We have carried out the stability analysis of the equilibrium states in which the analytical results show that the disease free equilibrium point is locally and globally asymptotically stable when ![]() and unstable when
and unstable when![]() . This result necessitates that the basic reproduction number, which is the expected number of secondary cases produced by a single infected individual during the entire infectious period of that particular individual in a completely susceptible population is a key non-dimension parameter that dictates whether the disease will spread or die out. When
. This result necessitates that the basic reproduction number, which is the expected number of secondary cases produced by a single infected individual during the entire infectious period of that particular individual in a completely susceptible population is a key non-dimension parameter that dictates whether the disease will spread or die out. When ![]() is increased or decreased above or below unity compels to the persistence or eradication of bubonic plague disease respectively. The decrease or increase of the basic reproduction number
is increased or decreased above or below unity compels to the persistence or eradication of bubonic plague disease respectively. The decrease or increase of the basic reproduction number
will as a result affects negatively or positively the flea’s infective period![]() , probability that rodent survive the infected class
, probability that rodent survive the infected class![]() , the adequate contact rate flea to human
, the adequate contact rate flea to human![]() , rodent’s infective period
, rodent’s infective period![]() , the probability that flea gets the disease from the rodent or human which are
, the probability that flea gets the disease from the rodent or human which are ![]() or
or ![]() respectively. The human infective period
respectively. The human infective period![]() , probability that human survive the infected class
, probability that human survive the infected class![]() , the rate at which fleas gets infected
, the rate at which fleas gets infected![]() , the adequate contact rate flea to rodent
, the adequate contact rate flea to rodent ![]() and the rate at
and the rate at
which human and rodent become exposed to the the disease which are ![]() and
and ![]() respectively. The endemic equilibrium point is also found to be locally and globally asymptotically stable whenever they exist. Using the model’s parameters values from literature reviewed in this paper and some estimated, we use the simulation to show the endemic equilibrium for Human, Rodent, Flea and pathogens in the environment are stable thus supports the analytical results. We observe that without intervention that controls the value of
respectively. The endemic equilibrium point is also found to be locally and globally asymptotically stable whenever they exist. Using the model’s parameters values from literature reviewed in this paper and some estimated, we use the simulation to show the endemic equilibrium for Human, Rodent, Flea and pathogens in the environment are stable thus supports the analytical results. We observe that without intervention that controls the value of ![]() to less than a unity bubonic plague may be very fatal and a life threatening disease whenever it occurs.
to less than a unity bubonic plague may be very fatal and a life threatening disease whenever it occurs.
Acknowledgements
We thank the Editor and the referee for their comments. Research of R. C. Ngeleja is funded by The Government of Tanzania through Nelson Mandela African Institution of Science and Technology (NM-AIST). This support is greatly appreciated.
NOTES
![]()
*Corresponding author.