1. Introduction
In the past decades, research on two-dimensional (2-D) discrete systems has rapidly increased due to their extensive practical applications in circuits analysis [1] , digital image processing [2] , signal filtering [3] and thermal power engineering [4] , etc. Thus, the study of 2-D systems is an attractive problem and a number of results have been presented in the literature. Among these results the stability analysis of 2-D discrete systems has been given in [5] - [15] . In [5] , the problem of robust stability analysis and stabilization for 2-D discrete uncertain systems described by the Fornasini-Marchesini (FM) second model has been studied and the sufficient conditions for 2-D discrete uncertain systems to be robustly stable have been given in terms of linear matrix inequalities (LMIs). A necessary and sufficient condition for the stability of 2-D discrete systems described by the FM first model has been derived in [13] . The problem of stability for linear discrete 2-D singular general model (GM) has been discussed in [14] and a sufficient condition for the internal stability of the 2-D singular GM has been derived in terms of LMIs. In [15] , the robust stability analysis problem for a class of uncertain 2-D discrete systems described by the FM second model has been studied and sufficient conditions in terms of LMIs have been derived to ensure the robust stability of the uncertain 2-D discrete systems. Lately, the solution to the guaranteed cost control problem for 2-D discrete uncertain systems has been presented by many authors [16] - [22] .
In recent years, the H¥ control problem for 2-D discrete systems has gained a great deal of interest and many important results have been obtained [23] - [26] . A major advantage of H¥ control is that its performance specification takes account of the worst- case performance for system in terms of the system energy gain. This is appropriate for system robustness analysis and robust control with modeling uncertainties and disturbances than other performance specifications, such as the LQ-optimal control specification [23] . In [24] , the solutions for the H¥ control and robust stabilization problems for 2-D systems described by the Roesser model using the 2-D system bounded realness property have been presented. The problem of H¥ static output feedback control for 2-D discrete systems described by the Roesser model and the FM second model has been addressed in [25] . In [26] , the problem of robust H¥ control for uncertain 2-D discrete systems described by the GM via output feedback controllers has been investigated.
Since, delay is encountered in many dynamic systems and is often a source of instability, much attention has been focused on the problem of stability analysis and controller design for 2-D discrete state-delayed systems in the last decades. Presently, the stability results for 2-D discrete state-delayed systems fall in two groups: delay-inde- pendent stability conditions [27] - [35] and delay-dependent ones [36] - [45] . The former refers to the stability conditions which do not depend on delay; the latter contains information on the size of delay. Generally speaking, the delay-dependent stability condition is less conservative especially when the sizes of the delays are small [45] . The problem of stability analysis for 2-D discrete state-delayed systems in the GM has been considered in [33] and sufficient condition for the stability has been derived via Lyapunov approach. In [27] , a solution to the problem of delay-independent H¥ control for 2-D state-delayed systems described by the FM second model has been presented. The problem of robust reliable control for a class of uncertain 2-D discrete switched systems with state delays and actuator faults represented by a model of Roesser type has been studied by [28] . In [35] , the problem of robust guaranteed cost control via memoryless state feedback for uncertain 2-D discrete state-delayed systems described by the FM second model has been considered. Several technical errors that have occurred in the main results of [35] were corrected in [30] . A solution to the guaranteed cost control problem via memory state feedback control laws for a class of uncertain 2-D discrete state-delayed systems described by the FM second model has been presented in [31] . The problem of delay?dependent guaranteed cost control via memoryless state feedback for uncertain 2-D discrete state-delayed systems described by the FM second model has been studied in [43] . In [41] , a delay-range dependent H¥ control and stabilization problem for a class of uncertain 2-D state-delayed systems described by the Roesser model has been proposed. The delay-dependent H¥ control problem via a delay-dependent bounded real lemma for a class of 2-D state-delayed systems described by the FM second model has been addressed in [40] . Recently, the problems of delay- dependent H¥ control for 2-D discrete state-delayed systems described by the FM second model and Roesser model have been considered in [42] [44] , respectively and a delay-dependent optimal state feedback H¥ controller has been obtained for both the models. It may be mentioned here that the criteria presented in [42] [44] do not consider the uncertainty in system parameters. In real-time applications, the parametric uncertainties cannot be ignored as they are the main source of instability and poor system performance. Hence, the delay-dependent robust optimal H¥ control for uncertain 2-D discrete state delay systems is an important and challenging problem. However to the best of authors’ knowledge, the delay-dependent robust optimal H¥ control problem for uncertain 2-D discrete state delay systems represented by the GM which is structurally distinct from FM second model and Roesser model has not been addressed so far in the literature.
This paper, therefore, investigates the problem of delay-dependent robust optimal H¥ control for a class of uncertain 2-D discrete state delay systems described by the GM. The approach adopted in this paper is as follows: We first derive an LMI-based sufficient condition for the existence of delay-dependent g-suboptimal state feedback robust H¥ controllers in terms of feasible solution to a certain LMI. Further, a convex optimization problem with LMI constraints is formulated to design a delay-dependent robust optimal H¥ controller which minimizes the H¥ noise attenuation g of the closed-loop system. The paper is organized as follows. Section 2 formulates the problem of delay- dependent robust H¥ control for a class of uncertain 2-D discrete state delay systems described by the GM and recalls some useful results. In Section 3, a solution to the problem of delay-dependent robust optimal H¥ control is presented. An example illustrating the potential of the proposed technique is given in Section 4.
Notations:
Throughout the paper, the following notations are used: Rn denotes real vector space of dimension n; 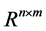 is the set of n ´ m real matrices; the superscript T stands for matrix transposition; 0 denotes null matrix or null vector of appropriate dimension; I is the identity matrix of appropriate dimension; G < 0 stands for the matrix G which is symmetric and negative definite; diag{….} stands for a block diagonal matrix;
is the set of n ´ m real matrices; the superscript T stands for matrix transposition; 0 denotes null matrix or null vector of appropriate dimension; I is the identity matrix of appropriate dimension; G < 0 stands for the matrix G which is symmetric and negative definite; diag{….} stands for a block diagonal matrix;  denotes the Euclidean vector norm. The
denotes the Euclidean vector norm. The  norm of a 2-D signal
norm of a 2-D signal 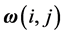 is given by
is given by
 , where
, where  is said to be in
is said to be in  if
if .
.
2. Problem Formulation and Preliminaries
Consider an uncertain 2-D discrete state delay system described by the GM [46] .
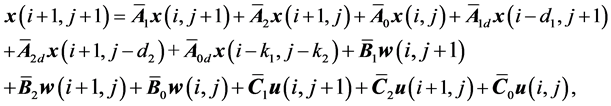 (1a)
(1a)
 (1b)
(1b)
where
 (1c)
(1c)
and  are horizontal and vertical coordinates, respectively,
are horizontal and vertical coordinates, respectively, 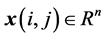 ,
,  are state and control input, respectively,
are state and control input, respectively, 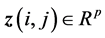 is the controlled output,
is the controlled output,  is the noise input with bounded energy i.e., it belongs to
is the noise input with bounded energy i.e., it belongs to . The matrices
. The matrices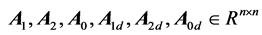 ,
, ![]() ,
,![]() ,
, ![]() and
and ![]() are known constant matrices represent- ing the nominal plant;
are known constant matrices represent- ing the nominal plant;![]() ,
, ![]() ,
, ![]() and
and ![]() are unknown constant positive integers representing delays. The matrices
are unknown constant positive integers representing delays. The matrices![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() represent parameter uncertainties in the system matrices which are assumed to be of the form
represent parameter uncertainties in the system matrices which are assumed to be of the form
![]() (1d)
(1d)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are known structural matrices of uncertainty and
are known structural matrices of uncertainty and ![]() is an unknown matrix representing parameter uncertainty which satisfies
is an unknown matrix representing parameter uncertainty which satisfies
![]() (or equivalently,
(or equivalently,![]() ). (1e)
). (1e)
For system (1), suppose a finite set of initial conditions [33] , i.e., there exist positive integers ![]() and
and![]() , such that
, such that
![]() (2)
(2)
Denote ![]() we first present the definition of asymptotic stability for the system (1).
we first present the definition of asymptotic stability for the system (1).
Definition 1. [42] The system (1) is asymptotically stable if ![]() with
with
![]() ,
, ![]() and the initial condition (2).
and the initial condition (2).
Introduce the following state feedback controller
![]() (3)
(3)
Applying the controller (3) to system (1) will result in the closed-loop system:
![]() (4)
(4)
where
![]() ,
, ![]() ,
,![]() .
.
T o investigate the delay-dependent ![]() control problem, we first define the vectors
control problem, we first define the vectors ![]() such that
such that
![]() (5)
(5)
The following well known lemmas are needed in the proof of our main result.
Lemma 1. [42] [44] For any matrices ![]() and
and![]() , and any integer
, and any integer![]() , the following summation inequality holds
, the following summation inequality holds
![]() (6)
(6)
where
![]()
Lemma 2. [5] Let![]() ,
, ![]() ,
, ![]() and
and ![]() be real matrices of appropriate dimension with
be real matrices of appropriate dimension with ![]() satisfying
satisfying ![]() then
then
![]() , (7a)
, (7a)
holds for all ![]() satisfying
satisfying![]() , if and only if there exist
, if and only if there exist ![]() such that
such that
![]() . (7b)
. (7b)
The ![]() performance measure for system (1) with the initial condition (2) is defined as follows:
performance measure for system (1) with the initial condition (2) is defined as follows:
Definition 2. [42] Given a scalar![]() , integers
, integers![]() ,
, ![]() ,
, ![]() ,
, ![]() and symmetric positive definite weighting matrices
and symmetric positive definite weighting matrices![]() . The closed-loop system (4), formed by system (1) with the initial condition (2) and state- feedback controller (3), is said to have an
. The closed-loop system (4), formed by system (1) with the initial condition (2) and state- feedback controller (3), is said to have an ![]() noise attenuation g for any delays
noise attenuation g for any delays![]() ,
, ![]() ,
, ![]() ,
, ![]() satisfying
satisfying![]() ,
, ![]() ,
, ![]() and
and ![]() if it is robustly stable and satisfies
if it is robustly stable and satisfies
![]() (8)
(8)
where
![]()
![]()
![]()
![]()
and![]() ,
, ![]() ,
, ![]() ,
, ![]() are upper bounds of delays in states.
are upper bounds of delays in states.
In the case when the initial condition is known to be zero, then the ![]() performance measure (8) reduces to
performance measure (8) reduces to
![]() . (9)
. (9)
Using the 2-D Parseval’s theorem [3] , (9) is equivalent to
![]() (10)
(10)
where ![]() denotes the maximum singular value of the corresponding matrix and
denotes the maximum singular value of the corresponding matrix and
![]() (11)
(11)
is the transfer function from the disturbance input ![]() to the controlled output
to the controlled output ![]() for the system (4).
for the system (4).
The objective of this paper is to design a controller of the form (3) such that the closed-loop system (4) is asymptotically stable and the ![]() norm of the transfer function (11) from the noise input
norm of the transfer function (11) from the noise input ![]() to the controlled output
to the controlled output ![]() for the closed-loop system (4) is smaller than g. Such controller is said to be a g-suboptimal state feedback robust
for the closed-loop system (4) is smaller than g. Such controller is said to be a g-suboptimal state feedback robust ![]() controller for the uncertain 2-D discrete state delay system (1) with any state delays
controller for the uncertain 2-D discrete state delay system (1) with any state delays![]() ,
, ![]() ,
, ![]() ,
, ![]() satisfying
satisfying![]() ,
, ![]() ,
, ![]() and
and![]() .
.
3. Main Results
In this section, we first present a delay-dependent approach to solve the ![]() control problem for the uncertain 2-D discrete state delay system (1) with any state delays
control problem for the uncertain 2-D discrete state delay system (1) with any state delays![]() ,
, ![]() ,
, ![]() ,
, ![]() satisfying
satisfying![]() ,
, ![]() ,
, ![]() and
and![]() . Based on Lemma 1, a sufficient condition for the existence of g-suboptimal state feedback robust
. Based on Lemma 1, a sufficient condition for the existence of g-suboptimal state feedback robust ![]() controllers is obtained in terms of an LMI. Further, a delay-dependent state feedback robust optimal
controllers is obtained in terms of an LMI. Further, a delay-dependent state feedback robust optimal ![]() controller is obtained by solving a convex optimization problem which minimizes the
controller is obtained by solving a convex optimization problem which minimizes the ![]() noise attenuation g of the closed-loop system (4).
noise attenuation g of the closed-loop system (4).
Theorem 1. The closed-loop system (4), formed by system (1) with the initial condition (2) and state-feedback controller (3), is robustly stable and has a specified ![]() noise attenuation g, if there exist matrices
noise attenuation g, if there exist matrices ![]() and symmetric positive definite matrices
and symmetric positive definite matrices ![]() satisfying
satisfying![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() such that
such that
![]() (12)
(12)
where
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Proof. To prove that the closed-loop system (4) with ![]() is asymptotically stable, we define a Lyapunov-Krasovskii function
is asymptotically stable, we define a Lyapunov-Krasovskii function
![]() (13)
(13)
where
![]()
![]()
![]()
and![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . Thus, it is explicit that
. Thus, it is explicit that![]() .
.
Along any trajectory of the system (1) with![]() , the increment
, the increment ![]() is given by
is given by
![]() (14)
(14)
Applying (5), we get
![]() (15)
(15)
Now applying Lemma 1, we get the following summation inequalities
![]() (16)
(16)
![]() (17)
(17)
and
![]() (18)
(18)
where ![]()
Now, substituting (15)-(18) in (14) yields
![]() (19a)
(19a)
![]() (19a)
(19a)
Applying Schur complement, it follows from matrix inequality (12) that
![]() (19b)
(19b)
Thus, from (19b), it implies that
![]() , (20)
, (20)
holds for any delays![]() ,
, ![]() ,
, ![]() and
and ![]() satisfying
satisfying![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Hence, the closed-loop system (4) with ![]() is asymptotically stable.
is asymptotically stable.
Next, we establish the ![]() performance measure of the closed-loop system (4) for
performance measure of the closed-loop system (4) for ![]()
We consider
![]() (21)
(21)
where
![]()
![]()
![]()
It follows from inequality (12) that
![]() (22)
(22)
Summing the inequality (22) over ![]() gives
gives
![]() . (23)
. (23)
Now,
![]() (24)
(24)
![]() (25)
(25)
Thus, by using (25) in (23), we get
![]() (26)
(26)
Since, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , therefore, it follows from Definition 2 that the closed-loop system (4) guarantees the
, therefore, it follows from Definition 2 that the closed-loop system (4) guarantees the ![]() noise attenuation
noise attenuation![]() . This completes the proof of Theorem 1.
. This completes the proof of Theorem 1.
In the following, we will show that the above derived sufficient condition for existence of delay-dependent robust ![]() controllers can be transformed to the solvability of an LMI.
controllers can be transformed to the solvability of an LMI.
Theorem 2. Consider the closed-loop system (4) with the initial condition (2). Given scalars![]() ,
, ![]() and integers
and integers![]() ,
, ![]() ,
, ![]() and
and![]() , if there exist matrices
, if there exist matrices![]() ,
, ![]() and symmetric positive definite matrices
and symmetric positive definite matrices ![]() such that
such that
![]() (27)
(27)
where
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
then the closed-loop system (4) with![]() ,
, ![]() ,
, ![]() and
and ![]() has a specified
has a specified ![]() noise attenuation g and the controller (3) with
noise attenuation g and the controller (3) with ![]() is a g-suboptimal state feedback robust
is a g-suboptimal state feedback robust ![]() controller for the uncertain 2-D discrete state delay system (1).
controller for the uncertain 2-D discrete state delay system (1).
Proof. It follows from matrix inequality (12) that![]() ,
, ![]() and
and ![]() are reversible. So, let us assume that
are reversible. So, let us assume that
![]() (28a)
(28a)
![]() (28b)
(28b)
![]() (28c)
(28c)
Pre-multiplying and post-multiplying both sides of matrix inequality (12) by
![]()
and its transpose, respectively, we get
![]()
![]()
![]()
![]() (29)
(29)
Denoting![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , we can re-write (29) as
, we can re-write (29) as
![]() , (30)
, (30)
where
![]()
![]()
![]()
![]()
Using (1d) and (1e), (30) can be expressed as
![]() , (31)
, (31)
where
![]() ,
,
![]() ,
,
![]()
Therefore, using Lemma 2, (31) can be rearranged as
![]() (32)
(32)
The equivalence of (32) and (27) follows trivially from Schur complements. This completes the proof of Theorem 2.
Theorem 2 provides a parameterized representation of a set of g-suboptimal robust ![]() state feedback controllers (if they exist) in terms of feasible solutions to the LMI (27). Based on Theorem 2, the design problem of a delay-dependent robust optimal
state feedback controllers (if they exist) in terms of feasible solutions to the LMI (27). Based on Theorem 2, the design problem of a delay-dependent robust optimal ![]() controller can be formulated as
controller can be formulated as
![]() (33)
(33)
which ensures the minimization of ![]() noise attenuation
noise attenuation ![]() of the closed-loop system (4).
of the closed-loop system (4).
4. An Illustrative Example
In this section, we present an application example to demonstrate the effectiveness of our proposed result.
Example 1. In this example, we shall illustrate the applicability of Theorem 2 to the control of thermal process in heat exchanger [4] [47] which can be expressed by the partial differential equation with time and space delays:
![]() (34)
(34)
where ![]() is the temperature at space
is the temperature at space ![]() and time
and time![]() ,
, ![]() is input function,
is input function, ![]() and
and ![]() are the time delays,
are the time delays, ![]() and
and ![]() are the space delays, and
are the space delays, and![]() ,
, ![]() ,
, ![]() ,
, ![]() , b are the real coefficients. Taking
, b are the real coefficients. Taking
![]() (35a)
(35a)
![]() (35b)
(35b)
(34) can be expressed in the following form:
![]() (36)
(36)
where![]() ,
, ![]() ,
, ![]() and,
and, ![]() ,
, ![]() is the integer function.
is the integer function.
It is assumed that the surface of the heat exchanger is insulated and the heat flow through it is in steady state condition, then we could take the boundary conditions as
![]() and
and![]() , respectively.
, respectively.
Denote![]() , it is easy to verify that (36) can be converted into the following discrete form:
, it is easy to verify that (36) can be converted into the following discrete form:
![]() (37)
(37)
Next, consider the problem of delay-dependent ![]() control for uncertain two- dimensional (2-D) discrete state-delayed systems characterized by (37). Let
control for uncertain two- dimensional (2-D) discrete state-delayed systems characterized by (37). Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and the initial state satisfies the condition (2) with
and the initial state satisfies the condition (2) with![]() ,
,![]() .
.
To consider the problem of ![]() disturbance attenuation, the thermal process is modeled in the form (1) with
disturbance attenuation, the thermal process is modeled in the form (1) with
![]() (38)
(38)
It is also assumed that the above system is subjected to the parameter uncertainties of the form (1c) and (1d) with
![]() (39)
(39)
Using the MATLAB LMI toolbox [48] [49] , it is found that the optimization problem (33) is feasible for the present example and the optimal solution is given by
![]() (40)
(40)
and a delay-dependent optimal ![]() state feedback controller
state feedback controller
![]() (41)
(41)
When![]() ,
, ![]() ,
, ![]() ,
, ![]() , the frequency response
, the frequency response ![]() from the disturbance input
from the disturbance input ![]() to the controlled output
to the controlled output ![]() for the system (4) is shown in Figure 1. It is apparent from Figure 1 that the maximum value of
for the system (4) is shown in Figure 1. It is apparent from Figure 1 that the maximum value of ![]() is 0.5081, which is below the specified level of attenuation
is 0.5081, which is below the specified level of attenuation![]() .
.
5. Conclusion
A solution to delay-dependent robust optimal ![]() control problem for a class of uncertain 2-D discrete state delay systems described by the GM with norm-bounded uncertainties has been presented. A sufficient condition for the existence of delay-de- pendent g-suboptimal state feedback robust
control problem for a class of uncertain 2-D discrete state delay systems described by the GM with norm-bounded uncertainties has been presented. A sufficient condition for the existence of delay-de- pendent g-suboptimal state feedback robust ![]() controllers has been established under the LMI framework. A delay-dependent state feedback robust optimal
controllers has been established under the LMI framework. A delay-dependent state feedback robust optimal ![]() controller is obtained through a convex optimization problem which can be solved by using MATLAB LMI toolbox [48] [49] . Finally, an application example has been provided to illustrate the effectiveness of the proposed technique.
controller is obtained through a convex optimization problem which can be solved by using MATLAB LMI toolbox [48] [49] . Finally, an application example has been provided to illustrate the effectiveness of the proposed technique.
Acknowledgements
The Authors would like to thank the editor and the reviewers for their constructive comments and suggestions.