1. Introduction
Shock wave appears in the form of a steep pressure gradient. When a supersonic flow is deflected by an object, e.g., a spacecraft, the airflow disturbances cannot get away from the object. These disturbances coalesce into a shock wave to introduce a discontinuity in the flow properties at the shock front location, where is the reachable edge of deflected flow disturbances from the object. Shock wave increases the pressure in front of the object, causing significant enhancement of the flow drag and friction on the object. Moreover, unsteady shock wave in supersonic flight produces notorious sonic boom on the ground. A physical spike [1] is currently used in a supersonic spacecraft to move original bow shock upstream from the blunt-body nose location to its tip location in the new form of a conical oblique shock to mitigate shock effects on the flight.
Thermal energy deposition in front of a flying body to perturb the incoming flow and shock wave formation has been studied [2] - [4] . The heating of the supersonic incoming flow results in a local reduction of the Mach number, which weakens shock wave and increases the shock angle. It is an effective approach to reduce the wave drag and shock noise in supersonic and hypersonic flows, however, the energy gain from drag reduction is much less than the injected heating energy. Nevertheless, this is a feasible approach for sonic boom attenuation.
Plasmas modification of the shock structure has been evidenced in a number of shock-tube experiments. Plasma can effectively convert electric energy to thermal energy for gas heating. Moreover, it has the potential to possibly offer a non-thermal modification effect on the structure of shock waves. The results exhibited an increased velocity and dispersion on shock waves propagating in the glow discharge region [5] . However, the main inspiration for the study of plasma effects on shock waves is attributed to the observation of a wind tunnel experiment conducted by Gordeev et al. [6] . High-pressure metal vapor (high Z) plasma, produced inside the chamber of a cone-cylinder model by exploding wire off electrical short circuit, was injected into the supersonic flow through a nozzle. A significant drag reduction was measured, which was too large to be accounted for by the thermal effect alone. In a subsequent wind tunnel experiments [7] [8] , the shock front increased dispersion in its structure in a decaying electric discharge plasma was observed. Implement a plasma torch module [9] in a cone-shape wind tunnel model for on-board periodic electric discharges, the results of a series of wind tunnel experiments [10] - [12] showed that the shock front increased dispersion in its structure and/or standoff distance from the model when plasma was generated ahead of a model. The detached curve shock increased shock angle and faded away as the discharge was intensified [10] . This cone model was truncated to represent a blunt body. The experiment showed that on-board pulsed electric discharges transformed the baseline bow shock to an attached oblique shock [13] . Computational and experimental studies [14] indicate that an added magnetic field can strengthen the arc plasma to further weaken the shock wave. On the other hand, microwave plasma projected on-board was shown still too weak to introduce any visible effect on the shock wave in a hypersonic flow [15] .
Shock wave angle b and structure depend on the Mach number M and the deflection angle q of the flow [16] , which can be modified via plasma deflection [17] to cause the modification of the shock structure observed in experiments [10] - [13] . Charged particles in plasma, accelerated by the applied electric field, deflect the flow through collisions. Electrons deflect the neutral flow through elastic collisions. The deflection is particularly effective when plasma is produced directly within the neutral flow. Ions moving through their own gas are subject to charge transfer between the ion and the neutral gas, a type of inelastic collision whose probability predominates over those of other interactions in the low ion energy regime [18] . Moreover, in air the charge transfer cross-section between 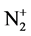 and N2 in the relevant energy regime is larger than 3 ´ 10−19 m2 [18] . An ion that has traveled a single charge-transfer free path becomes a neutral particle but retains its velocity, which is usually low. Most of the converted neutrals move at subsonic speed; these particles do not contribute to the shock wave formation. Some of them may move at supersonic speed; however, they do not drift together, and thus the produced disturbances off the model are expected to spread out in the form of expansion waves, rather than coalesce into shocks. The ions converted from neutrals through charge-transfer are collected by the cathode and do not contribute to the shock wave generation either.
and N2 in the relevant energy regime is larger than 3 ´ 10−19 m2 [18] . An ion that has traveled a single charge-transfer free path becomes a neutral particle but retains its velocity, which is usually low. Most of the converted neutrals move at subsonic speed; these particles do not contribute to the shock wave formation. Some of them may move at supersonic speed; however, they do not drift together, and thus the produced disturbances off the model are expected to spread out in the form of expansion waves, rather than coalesce into shocks. The ions converted from neutrals through charge-transfer are collected by the cathode and do not contribute to the shock wave generation either.
In the present work, new data demonstrating the plasma mitigation of shock wave are presented. A plasma deflector was generated by electric discharge on-board of a wind tunnel model. The attenuation or ideal elimination of shock wave formation around the periodic discharge model was observed. The anticipated results of reduced fuel consumption and having smaller propulsion system requirements, for the same cruise speed, will lead to the obvious commercial gains that include larger payloads at smaller take-off gross weights and broadband shock noise suppression during supersonic flight. These gains can make commercial supersonic flight a reality for the average traveler. In Section 2, experimental setup and operation are described. The experimental results are presented in Section 3. Physical mechanism of air plasma mitigation of shock wave is discussed in Section 4. Conclusion is drawn in Section 5.
2. Experimental Setup
Experiments were conducted in the test section, with a 0.38 m ´ 0.38 m cross section, of a supersonic blow-down wind tunnel, shown in Figure 1(a). The upstream airflow had a flow speed v = 570 m/s, temperature T1 = 135 K, and a pressure P1 = 0.175 atm.
2.1. Wind Tunnel Model
The wind tunnel model has a truncated-cone body connected to a cylindrical body
![]()
Figure 1. (a) Mach 2.5 wind tunnel for performing the experiment, (b) schematic of the wind tunnel model implemented with electric discharge electrodes for plasma generation and (c) a photo of the arc discharge in a supersonic flow.
attached to a holder. It also consists of a sharpened solid tungsten rod of a diameter d = 2.4 mm, held by a ceramic insulator, in place concentrically with the truncated-cone body to form the electrodes for the discharge. The cone-shaped ceramic insulator together with the tungsten rod set as a short protruding spike replaces the truncated part of the cone. The schematic of the model is presented in Figure 1(b). The truncated 600 cone has a frontal diameter D = 11.1 mm and a height L = 12.7 mm. The cylindrical base of the cone has a diameter Db = 25.4 mm. The distance from the tip to the edge of the truncated-cone surface is about 5 mm.
2.2. Periodic Discharge
A half-wave rectified 60 Hz power supply was used for periodic discharge. The wind tunnel model is grounded and the spike is connected to the negative output voltage of the power supply. The discharge initiates in the region near the tip of the spike, where concentrated electric field pushes generated electrons to the upstream region. The produced spray-like plasma shown in Figure 1(c) acted as a spatially distributed deflector, which deflected the incoming flow.
The breakdown voltage in the absence of the flow is about 4.5 kV (for 5-mm gap). During the run, the background pressure dropped; it reduced the gas breakdown voltage to about 3.3 kV. In the run, the electric field intensity near the tip exceeds 1 MV/m before breakdown occurs and drops quickly to a level less than 50 kV/m as the discharge current reaches the peak. The peak and average power of the discharge are about 1.2 kW and 100 W, respectively. The peak electron density is estimated to exceed 1019 electrons/m3 [9] .
2.3. Optical Diagnostics
Shadowgraph method was used to optically diagnose the flowfield around the spike and nose of the cone. A black and white (BW) charge coupled device (CCD) camera, with a frame rate of 30 frames per second and exposure time of 1/60 s (which is slightly less than four times of each discharge period), was used to record directly the shadowgraph images of the flow dynamics. A video (color CCD) camera as the corresponding one to the BW CCD camera was used to record the spatial distribution and temporal evolution of the plasma glow with the same frame rate and exposure time. The video graph recorded in each frame is an integrated result over the exposure time, and thus the temporal variation of the shock wave structure and plasma glow during a single discharge period cannot be recorded directly.
Continuous video graph of the flow can still reveal important information regarding the dynamic behavior of the flow field when two consecutive frames can be extracted because the discharge does not have a constant period. Moreover, the results extracted from videotapes recording the shadowgraph images of the flow and plume images of plasma can provide the correlation between the plasma distribution and the modification of the shock structure. It helps to deduce required plasma conditions to achieve significant plasma effect on the shock wave.
2.3.1. The Shadow Imaging System
A schematic of the optical setup for simultaneous Shadow and Plasma Glow/Afterglow video imaging is shown in Figure 2. An incandescent lamp with beam-forming optics and filters was used for the present reported observations. A parabolic mirror, of diameter 0.3 m and focal length of 3.7 m, collimated the divergent beam from the (point) light source before it passed through the wind tunnel test section windows. On the other side of the wind tunnel, an image forming optics, consisting of a lens and a B&W high resolution CCD camera, was used to obtain the Shadow images. The Shadow images were projected directly on the CCD area, avoiding the use of projection screens, and recorded at a rate of 30 frames/sec with an exposure time of 1/60 sec. The image magnification could be modified in the range 0.1 - 0.5 mm/pixel by camera positioning along the optical axis. Neutral density filters were used to cut down light intensity coming from the flow itself, instigated by the discharge.
2.3.2. The Plasma Glow/Afterglow Imaging System
For plasma visualization, we used a color CCD camera positioned on either side of the wind tunnel, at a small angle with respect to the optical axis of the system. This video camera recorded at a rate of 30 frames/sec with selectable exposure time from 1/60 to 1/4000 sec. A neutral density filter was applied to the CCD camera for reducing the airglow intensity of the discharge entering the camera. The synchronization between Shadow and plasma glow recorded images was realized by post-processing of the corresponding images (based on the discharge glow that has temporal resolution of less than 100 msec). Tracking of video frames showed that the frame synchronization error between cameras during one-run duration (100 - 300 frames) was less than half frame that was less than 1/60 sec.
![]()
Figure 2. Schematic of an optical setup.
3. Experimental Results
The modification effect depended on the density and volume of the plasma deflector produced by each discharge, which is in short pulse. This time varying deflector caused the shock structure and its front position to vary in time. Although the temporal variation of the shock wave structure during a single discharge period could not be recorded directly, the desired information regarding the transient behavior of the flow field was revealed in each pair of consecutive frames extracted from the continuous shadow graphy of the flow. This is demonstrated in Figure 3, which includes a sequence of four pairs of shadowgraphs showing the repeating response of the shock wave to the plasma deflector. In this and other shadowgraphs and plasma plume images presented later, the flow is from left to right. In Figure 3, the shadowgraphs in the left panel show a
![]()
Figure 3. A sequence of four shadowgraphs (in the left panel) show a steady state baseline shock generated in front of the wind tunnel model during a wind tunnel run at Mach 2.5. The subsequent video frame of each shadowgraph is presented on its right hand side to show the flow response to the plasma deflector generated by an electric discharge.
steady state baseline shock generated in front of the wind tunnel model. The plasma effect on the baseline shock is then shown by the shadowgraphs in the right panel, in which each one is a consecutive video frame to the one on the left. Because of the variation of the starting time of each discharge, the different modifications of the shock structure shown in the right panel shadowgraphs manifest the dependency of the shock wave mitigation on the intensity of the plasma deflector. As seen, the baseline shock is split into two, with a new one moved upstream; the original baseline shock becomes very weak and the new one is a curved one with larger shock angle. As the curved shock front moves upstream, it becomes diffusive with increasing shock angle. It is eventually eliminated and the original baseline shock spreads out becoming expansion waves.
The growth of the plasma deflector may be manifested by the increase of the background brightness in the shadowgraphs. Based on this, a time sequence of four shadowgraphs (a) to (d) is assembled to imitate the flow response to the intensifying plasma deflector (e) to (h) during one discharge period in the middle of a wind tunnel run at Mach 2.5. First, the shadowgraph shown in Figure 4(a) is in the situation that the discharge is in the early stage. The shadowgraph still records the baseline shock. The next
![]()
Figure 4. An assembled time sequence of four shadowgraphs (a)-(d) to represent the flow response to the plasma deflector (e)-(h) during one discharge period in the middle of a wind tunnel run at Mach 2.5.
two presented in Figure 4(b) and Figure 4(c) correspond to the situation that the discharge is intensifying before reaching the peak. The baseline shock front is first split into two (Figure 4(b)), with a new one located upstream; the curved new one becomes weaker and more diffusive as the plasma deflector is further intensified (Figure 4(c)). As the plasma deflector is intensified to reach the peak, its modification effect on the shock structure also reaches the maximum. As shown in Figure 4(d), the curved new one disappears and the remaining structure becomes diffusive in the form of expansion waves.
In sum, the discharge transforms the shock from a well-defined attached shock into a diffused and highly curved shock structure, which moves upstream with increasing shock angle and fades away. This observed process suggests that the flow deflection by symmetrically distributed plasma (Figure 4(e) to Figure 4(h)) upstream of the shock is likely the main attribution to the plasma mitigation of the shock wave.
4. Discussion
The plasma deflector is introduced at a location in front of the model by an on-board electrical discharge, which is triggered by a negative voltage applied between the grounded body of the cone and the tip of the cone which is insulated from the body. The sharp tip helps to enhance the electric field intensity in the region in front of the tip. Take the planar projection of the wind-tunnel model as a two-dimensional model, the equipotential lines between the two electrodes, with the central electrode biased negatively, are evaluated numerically by using a Poisson solver. The result is presented in Figure 5(a), in which the distribution of the electric field that is perpendicular to the equipotential line is also indicated. As shown, the applied electric field can extend to a relatively large region upstream of the baseline shock front, regardless the electric field intensity decreases with distance from the tip. This local field continuously accelerates electrons in the upstream region to deflect the incoming flow via elastic collisions. Cartoon figures to illustrate the flow deflection are presented in Figure 5(b) and Figure 5(c). The deflection is most effective when plasma has a symmetric distribution around the tip. This is because the net change of the transverse momentum of the flow is zero; it makes easy to satisfy momentum conservation in large deflection situation. The charge transfer cross-section between  and N2 in the relevant energy regime is larger than 3 ´ 10−19 m2. Thus, ion plasma also contributes significantly to deflect the incoming flow. Through charge transfer process, molecular nitrogen ions (
and N2 in the relevant energy regime is larger than 3 ´ 10−19 m2. Thus, ion plasma also contributes significantly to deflect the incoming flow. Through charge transfer process, molecular nitrogen ions (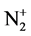 ) are converted to randomly distributed neutrals (N2). On the other hand, those converted ions in the supersonic flow will be held in the discharge region by the applied electric field and then collected by the spike-cathode; thus the converted ion flow does not contribute to the shock wave generation. The charge transfer process increases the entropy of the flow, decreases the equivalent Mach value of the flow, and enhances flow deflection.
) are converted to randomly distributed neutrals (N2). On the other hand, those converted ions in the supersonic flow will be held in the discharge region by the applied electric field and then collected by the spike-cathode; thus the converted ion flow does not contribute to the shock wave generation. The charge transfer process increases the entropy of the flow, decreases the equivalent Mach value of the flow, and enhances flow deflection.
We now apply Taylor-Maccoll’s theory to explain the effect of flow deflection on the shock structure. The solution of the Taylor-Maccoll equation represents an attached shock generated by a cone in a supersonic flow. When the cone angle exceeds a maximum value, i.e., qc > qcmax, attached shock solution does not exist and the shock becomes detached [16] . Because qcmax decreases with the decrease of the Mach value of the flow and the equivalent cone angle qc increases with the increase of flow deflection, qc > qcmax situation can occur when plasma deflector is introduced. This theory facilitates the understanding of the experimental observations that the on-board generated plasma deflector causes the shock to move upstream to become detached curve shock, which increases standoff distance from the model and becomes more and more diffusive as the plasma deflector is intensified. A shock-free state is then reached. These observations are summarized in a superimposed shadowgraph presents in Figure 6(a), which shows an attached baseline shock front, and three modified by the plasma with increasing discharge intensity: an attached shock front having larger shock angle and two detached shock fronts. The evaluated Mach number distributions corresponding to the three modified shock fronts are presented in Figure 6(b). As shown, the effective Mach number of the flow decreases significantly as the discharge is intensified.
![]()
Figure 5. (a) Distributions of the equipotential line and electric field between two electrodes of a two-dimensional model and (b) & (c) cartoons showing the envisioned electric discharges and the deflection of the incoming flow by the discharge-produced plasma, causing the disappearance of the shock wave.
![]()
Figure 6. (a) A superimposed shadowgraph showing the (attached) baseline shock front, and three plasma mitigated shock front: one attached shock front with larger shock angle and two detached shock fronts, corresponding to increasing discharge intensity and (b) M1(x), the Mach number, of an incoming flow after being scattered by a plasma deflector; decreasing M1 corresponding to increasing discharge intensity.
5. Conclusions
The wave drag of the shock on the cone depends on the strength of the shock, which in turn depends on the Mach number of the flow. It is found that the effective Mach number M1(x) of the deflected flow in the tip region of the wind tunnel model is smaller than M10 = 2.5. A decrease in the effective Mach number of the incoming flow in the tip region verifies that this air plasma deflector can indeed reduce the wave drag of the shock on the cone. Moreover, the modified shock structure moves upstream away from the cone; it also results to the reduction of the wave drag on the cone.
The experimental results conclude that it is feasible to apply a non-thermal air plasma deflector for the attenuation or ideal elimination of shock wave formation around a supersonic vehicle. The anticipated results of reduced fuel consumption and having smaller propulsion system requirements, for the same cruise speed, will lead to the obvious commercial gains that include larger payloads at smaller take-off gross weights and broadband shock noise suppression during supersonic flight. These gains can make commercial supersonic flight a reality for the average traveler.
Acknowledgements
The author is grateful to Dr. D. Bivolaru for collaborative work. This work was supported in part by the Air Force Office of Scientific Research Grant AFOSR-FA9550- 04-1-0352.