Optimum Simultaneous Allocation of Renewable Energy DG and Capacitor Banks in Radial Distribution Network ()
1. Introduction
There is an increase in world economy with the increase in load demand which demands the high quality uninterrupted power supply. Due to the ruination of monopoly system and technology advancements, the small scale power generation owners have been able to enter the competitive electricity market with the on-site renewable energy based DG systems [1] . The distributed generation technologies generally include solar photo voltaic, fuel cells, diesel engines and gas turbines (bio mass). The integration of capacitor banks with DG provides the necessary reactive power compensation to the network thereby reducing the line losses in the network. The simultaneous allocation of DG and capacitor banks can lead to an upturn of feeder capacity, reduction in real and reactive power losses, and the voltage profile improvement in radial distribution networks. The optimal simultaneous placement of DG and capacitor is a non-convex problem and thus the attainment of the global optimum solution may be reduced by the local optimum solutions. Due to the discrete nature of the problem, a large number of alternate solutions may be attained which will claim more high computational time. To achieve the optimum allocation of DG for real power loss reduction with multiple constraints the SADE algorithm is applied by VL Huang et al. without presenting any additional parameters [2] . Manafi et al. applied the modified PSO and dynamic PSO as well as improved differential evolution algorithm for optimal allocation of DG in RDN [3] . The objective considered by them was the real power loss minimization with the minimum installed real power DG in RDN. In literature [4] , the results of optimal allocation of DG using PSO with the genetic algorithm were compared. The PSO gave the better characteristic results in terms of solution quality, iteration and time for computation. The PSO for line loss reduction in power system subjected to voltage constraints for optimum placement of DG was performed by Wong et al. [5] . Jagadeesh Gunda et al. (2011) had applied the differential evaluation algorithm (DEA) to determine the optimal location and size of shunt capacitors and DGs in RDN for minimum real power loss on Indian Electricity Board benchmark 25 bus distribution systems [6] . The distributed generations are mainly classified according to the main fuel used. According to the fuel used, it is categorized as renewable energy DG and non-renewable energy DG. The non-renewable DG includes diesel generator, micro turbine, gas turbine etc. The renewable energy DG consists of wind farm, solar photovoltaic system, biomass plants etc. In this paper, for real power loss minimization the solar photovoltaic (SPV) and wind energy based renewable DGs are considered for integration with capacitor banks in RDN. Based on their real and reactive power generation capacity they are modeled as follows [7] - [9] (Table 1).
In this paper two types i.e. (SPV and wind) of renewable energy DG systems are considered for optimal allocation of DG. A two-stage methodology based on distributed
![]()
Table 1. Types of DG and their modeling.
generation sitting index (DGSI) ranking is used for simultaneous allocation of DG and capacitor banks. Initially the DGSI is determined for finding the optimal location of DG. To determine the optimal sizing in the preferred location the WIPSO and SADE algorithms are applied and the obtained results are compared.
2. Problem Formulation
The objective of the optimization problem is considered as
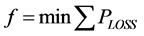. (1)
PLOSS is known as
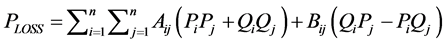. (2)
In Equation (2)
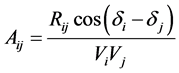(3)
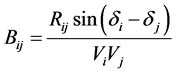(4)
Pi and Pj are the real power injection in bus i and bus j, respectively.
Qi and Qj are the reactive power injection in bus i and j, respectively.
Rij is the resistance between with ith and jth bus.
Vi and Vj are the voltage profile at ith bus and jth bus, respectively.
δi and δj are the angle of voltage of ith bus and jth bus, correspondingly.
For DG insertion
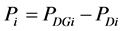(5)
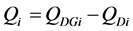(6)
The equality and inequality constraints are as follows.
Equality Constraints
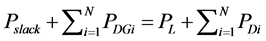(7)
Inequality constraints
where
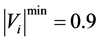and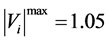 
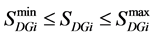
where
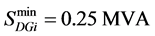and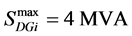 
Bus 2 ≤ position of DG ≤ bus n
P1 ≠ P2
where P1 and P2 are the bus location of DG and capacitor banks at position 1 and position 2 respectively.
3. Methodology
3.1. DGSI Ranking Method
In developing countries like India, the voltages at the remote end of the distribution feeders are greatly low with decreased voltage regulation since the rural distribution feeders are too long. Therefore, the bus voltage sensitivity of the node is to be considered for the DG placement in addition to the loss reduction, to produce the optimum result with reduced DG size and increased voltage profile. The DGSI is described in [10] .
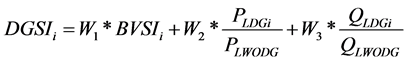(8)
where
. (9)
The value of BVSI from the literature [11] is as follows
(10)
By introducing DG size of 25% of feeder capacity in a bus other than the reference bus DGSI is found out using Equation (8). Thus DGSI is determined at all locations. Then the bus with least DGSI value is selected as the location for the insertion of DG. Then the size of DG is varied such that it produces minimum real power loss. This procedure is applied to both the type of DGs to determine the optimum size and location for real power loss minimization and the results are recorded. By implementing the DGSI ranking method, the determined optimum allocation is such that it reduces the real power loss with simultaneous improvement of voltage sensitivity of the radial distribution network.
This DGSI based approach determines the optimal location of DG unit primarily then the optimum size that should be placed in that location such that the minimum real power loss occurs. If only DG placement is essential this procedure is stopped here itself. This method is repeated for allocation of capacitor banks by considering the capacitor banks as a pure reactive power generator. (i.e. PDG = 0 & QDG = QDGi.)
Then the location is determined by altering the base system by introducing a DG with optimum DG size into the radial distribution system. After determining the location, the optimum size of capacitor bank is found out. Since the DG and capacitor banks are incorporated to the RDN one by one, the sizes found using this analytical approach are local optima not global optimum solution. Hence to determine the global optimal solution the WIPSO and SADE algorithms are used.
3.2. SADE Algorithm
The Differential Evolution (DE) is an evolutionary computational algorithm that applies comparatively pronounced selection and less stochastic approach to solve the optimization problems [12] . The significant characters of DE are its simplicity in structure, fast convergence, robustness and solution quality. The DE algorithm consists of three basic genetic operations; mutation, cross over and selection. After the initialization of population, the next generation population (G + 1) is created by this three basic operations using the current generation G.
Even the differential evolution is considered as accurate, reliable and fast convergence optimisation technique, the operator is required to set the values of control parameters of DE for each problem. Such parameter tuning is a time consuming process [13] . Using the self-adaptive differential evolution algorithm the time complexity does not increase since the user does not need to adjust the mutation parameter, cross over parameter and number of population. Hence self adaptive differential evolution algorithm can be implemented where the parameter tuning is not required [14] .
3.3. WIPSO Algorithm
The velocity equation of standard PSO is represented as the sum of three terms. The first term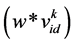 
characterizes the current velocity of the particle and can be considered as a momentum term. The second term is connected with a local search and indicates the particles best position from its current position. The third term is related with global search and indicates the global best position. The whole standard PSO process is the searching process that particle depends on its memory capability and share the information to trace the best solution. In early stage of PSO, the Pbest and Gbest vary frequently; the algorithm has the well-built global search capacity and the fast convergence characteristics. But at the end stage the Pbest and Gbest values get stabilisation and the first term nearly drops to zero value. At this instant, the updating of position goes to stagnation and the algorithm provides the local optima. It is the main disadvantage of the standard PSO.
To improve this shortcoming of PSO and produce better results, the weight improved PSO is proposed. This algorithm alters the inertia weight w value to improve the global search ability in the early stage and local search ability in the end stage.
![]()
(11)
![]()
(12)
Here k represents the current iteration and kmax is the maximum of iteration.
The velocity update equation is as follows
![]()
(13)
![]()
(14)
In this paper for simultaneous optimal allocation DG and capacitor banks , the SADE and WIPSO algorithms are applied.
4. Results and Discussion
A two-stage methodology is followed for the simultaneous allocation of DG and capacitor banks in the RDNs. Initially the locations of DG and capacitor bank are found out using DGSI ranking method. Here the location of capacitor bank is identified after changing the base case data of RDN with the insertion of DG of optimum size at optimum location. After determining the location of DG and capacitor banks, the SADE and WIPSO algorithms are applied for the simultaneous allocation of DG and capacitor bank in RDN and the results are compared. Table 2 and Table 3 show the results for standalone placement of DG and capacitor bank in the IEEE 33 bus and IEEE 69 bus RDN. From Table 2, it is understood that the SPV based DG improves the percentage of real power loss and reactive power loss reduction compared to wind based DG in both the test networks. From Table 3, it is understood that the standalone placement of capacitor bank in both the test works minimizes the real and reactive power loss occurred in the network by providing the reactive power support. Hence in this paper, it is decided to combine both DG and capacitor in RDN thereby to get the additional benefits in system loss reduction. For the combined allocation of DG and capacitor bank simultaneously the SADE and WIPSO algorithms are used and the results are recorded in Table 4.
Figure 1 shows that the both the real and reactive power losses occurred in the RDN gets minimized with the insertion of both renewable energy DG i.e. SPV and wind
![]()
Table 2. Optimum allocation results of DG alone in RDNs using DGSI ranking method.
![]()
Table 3. Optimum allocation results of Capacitor in RDNs using DGSI ranking method.
![]()
Table 4. Simultaneous allocation of DG and capacitor in RDN.
![]()
Figure 1. Real and Reactive power loss with the standalone placement of DG and capacitor bank.
DG. The capacitor banks introduced in the RDN also minimize the real and reactive power losses in the system. The SPV based DG minimizes the real and reactive power losses efficiently in the system than the wind based DG since it supplies only real power to the system. The wind based DG supplies real power to the RDN and absorbs the reactive power from the network. Hence its performance in real and reactive power loss reduction is not efficient. But the capacitor banks which supply only reactive power to the RDN reduces both the real and reactive power losses to some extent. The performance of wind DG in system loss reduction can be improved by its combined placement with capacitor banks.
It is evident from Table 4, that the simultaneous allocation of DG and capacitor bank in the RDN improves both the real and reactive power loss minimization occurred in the network. The performance of wind based DG in loss reduction improves more with the combined placement of capacitor bank. In IEEE 33 bus RDN, the percentage of real power loss reduction is 24.95% with the standalone placement of wind DG which gets improved to a value of 60.36% and 60.46% with the combined placement of capacitor bank using SADE and WIPSO algorithms. Similarly in IEEE 69 bus system it is improved from 31.85% to 89.13% and 89.16% using SADE and WIPSO algorithms.
In this work, the SADE and WIPSO algorithms obtain the locations of distributed generation identified by DGSI ranking method. For the simultaneous allocation of DG and capacitor bank, these algorithms get the locations of DGs as input to find the optimum sizes of DGs such that the minimum real power losses occurred in the RDNs. The benefits of relieving the SADE and WIPSO algorithm from the calculation of position of DGs are the less computational time and the enhanced convergence characteristics. Compared to SADE algorithm, the WIPSO algorithm has the fast convergence characteristics and less computational time (22.1 seconds). Whereas the computational time of SADE algorithm is 26 seconds. But, due to the good convergence character of the SADE algorithm, it produces the better optimal solutions than the WIPSO algorithm. The above said properties of SADE algorithm and WIPSO algorithm opens the door for researchers to develop a new hybrid algorithm by using the combinations of both these algorithms.
5. Conclusion
This paper is essentially concerned with the optimal allocations of DG and capacitor banks simultaneously in RDN using the SADE and WIPSO algorithms. Both the SADE and WIPSO algorithms produce the good results for real power loss minimization in the test networks. The SADE algorithm produces the good optimum solution than the WIPSO algorithm and the WIPSO algorithm has the fast convergence characteristics which makes it suitable for online applications. The results prove that the simultaneous allocation of DG and capacitor bank improves the real and reactive power loss reduction more effectively than their standalone placement. The performance of wind based DG in system loss reduction is ineffective with its standalone placement but its combined placement with capacitor banks enhances the system loss reduction. The installation of the renewable energy DG and capacitor bank at the potential locations reduces the system losses effectively. The results support the penetration of renewable energy in RDN and thereby make the power system as environmental friendly. The addition of practical constraints such as the load variation with the time period and distinct sizes of DG ratings into the proposed problem is the future work of this research.
Acknowledgements
The authors would like to express their sincere and the heartfelt thanks to the Principal and Management of
AAA
College of Engineering and Technology and Thiagarajar College of Engineering and Technology for their Constant support and encouragement towards the success of this research work.