R & D-Based Growth Model with Nominal Wage Stickiness

Shunsuke Shinagawa¹, Tomohiro Inoue²

¹Faculty of Economics, Kanagawa University, Yokohama, Japan.
²Faculty of Economics, Komazawa University, Tokyo, Japan.

DOI: 10.4236/tel.[phone]                

Abstract

In this study, we introduce nominal wage stickiness into an endogenous growth model based on R & D. This study examines how money growth affects long-run economic growth. We find that there exists a unique balanced growth path for sufficiently high rates of money growth, and that the economy exhibits sustained growth based on sustained R & D. Faster money growth results in greater employment and faster economic growth along such a balanced growth path. Furthermore, under some parameter restrictions, no balanced growth path exists for low rates of money growth; the economy is trapped in a steady state without long-run growth. These results suggest that money growth may be an important factor for long-run economic growth.

Keywords

Endogenous Growth, New Keynesian Phillips Curve, Nominal Rigidities, Monetary Growth Theory

1. Introduction

This study proposes a new monetary growth model involving price stickiness and endogenous R & D. Short-run macroeconomic models usually consider price stickiness, as in new Keynesian models. In this study, we introduce nominal wage stickiness into a long-run growth model based on R & D and investigate how money growth affects long-run output, employment, and economic growth.

We base the dynamics of our model on the new Keynesian Phillips curve (NKPC), under which money is not super neutral, even in the long run¹. [2] [3] proposed the Dynamic General Equilibrium (DGE) model with the NKPC and technological change, in which money is not super neutral in the long run and the long-run output gap exists when the monetary growth rate is below that of technological change. However, their analyses assumed exogenous technological change. This study proposes a DGE model based on the work of [2] with endogenous technological change rather than exogenous growth by introducing explicit R & D activities.

We focus on the steady-state economic growth and employment. For sufficiently high money growth rates, there is a unique balanced growth path, and the economy exhibits sustained growth based on sustained R & D. Faster money growth causes greater employment and faster economic growth along the balanced growth path. Furthermore, under some parameter restrictions, there is no balanced growth path for low money growth rates, and the economy is trapped in a steady state without long-run growth. These results suggest that money growth may be an important factor for long- run economic growth. That is, financial authorities are required to maintain high money growth rates to achieve sustained and faster economic growth.

Most of the preceding theoretical studies on money and endogenous growth have concluded that a higher money growth is associated with a lower rate of long-run growth, which is contrary to the conclusion of this study. See for example [4] - [8] . In contrast, [9] [10] have demonstrated the positive relationship between a monetary expan- sion and long-run growth using the infinitely lived overlapping-generation models. Some studies such as [11] - [13] proposed endogenous growth models that introduced nominal rigidities. [11] investigated how the volatility of monetary policy affects output growth under price and wage stickiness. [12] studied optimal monetary policy by using an endogenous growth model with a sticky price due to Calvo pricing, and showed that the optimal steady-state inflation rate is zero. [13] proposed an endo- genous growth model with sticky wage due to staggered Taylor wage contracts, and found a nonlinear relationship between money growth and long-run economic growth. In these studies, sustained growth becomes endogenous through learning-by-doing or simple externality, which differ from our study focusing on R & D as the engine of economic growth². This study proposes a new channel attributed to nominal rigidities and endogenous R & D through which money growth influences the long-run economic growth.

Some empirical studies argued that inflation has a negative impact on economic growth ( [15] - [17] ). However, [18] [19] pointed out that the negative correlation between inflation and growth is not robust. [20] concluded that growth and inflation are negatively related only in the extremely high inflationary economy. Furthermore, a number of empirical studies showed positive relationships between inflation (or money growth) and economic growth for advanced countries. See for example [21] - [26] ³. Our study provides a theoretical explanation for these empirical results.

The remainder of this paper is organized as follows. Section 2 sets up the model used in our theoretical investigation. Section 3 derives the law of motion and the steady state, which characterize the equilibrium path of the economy. It also investigates the existence and the uniqueness of the steady state. Section 4 concludes the paper.

2. Model

We consider the continuous-time version of the dynamic model based on [2] [27] . Let us assume an economy populated by many infinitely-lived households under monopolistic competition in the labor market, and there are rigidities of nominal wage. There is a single final good, which is produced using intermediate goods and supplied competitively. A new variety of intermediate goods is invented by allocating labor for R & D activities, and inventors enjoy infinitely-lived monopoly power. The available inter-mediate goods are produced by multiple intermediate firms using labor. Finally, we use the simple monetary policy rule under which financial authorities expand money supply at a constant rate.

2.1. Employment Agency

The manufacturing and R & D sectors regard each household's labor as an imperfect substitute for any other household's labor. To simplify the analysis, we assume that an employment agency combines differentiated labor forces into a composite labor force

according to the Dixit-Stiglitz function, , and supplies com-

posite labor to the intermediate goods and the R & D sectors. 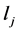denotes differentiated labor supplied by household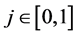, and l is the composite labor force. The number of households is normalized to 1. 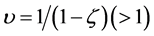is the elasticity of substitution between each pair of differentiated labor inputs.

Cost minimization of the employment agency yields the demand functions for dif- ferentiated labor j, 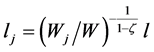, where 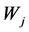denotes the nominal wage rate of labor force j, and W denotes the nominal wage rate of the composite labor force, which is given by.

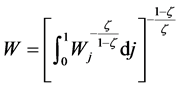2.2. Final Goods Sector

We assume that perfect competition prevails in the final goods market. The final goods firm produces the quantity y according to the Dixit-Stiglitz function,

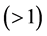where is the quantity of intermediate goods indexed by, and represents the elasticity of substitution between every pair of intermediate goods. N is the number of available intermediate goods and represents the technology level of the economy. The final goods firm faces diminishing returns with each intermediate good; therefore, greater values of N imply higher productivity.

Cost minimization by the final-goods producing firm yields the following demand functions for intermediate goods:

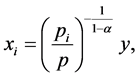(1)

where 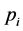is the price of intermediate goods i, and p is the price of the final good or the price level, which is given by.

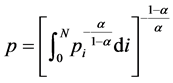2.3. Intermediate Goods Sector

Each intermediate good is produced using one unit of composite labor; thus, marginal cost is equal to the nominal wage level, W. Because patents have an infinite life, all intermediate goods are supplied monopolistically. Maximization of the monopoly pro- fit, , subject to the demand function (1) yields

(2)

where represents the amount of composite labor allocated to the production of the intermediate goods. All intermediate goods enter symmetrically into production of the final good. Moreover, the maximized monopoly profit is

(3)

From (2), the market equilibrium levels of output, y, and the price of the final good, p, are obtained as

(4)

(5)

We can rewrite (5) as

2.4. R & D Sector

The number of intermediate goods, N, expands according to the following equation:

(6)

where is the parameter that reflects the productivity of R & D. represents the amount of composite labor allocated to R & D, and clearing the labor market requires.

In equilibrium, the following free-entry condition must be satisfied:

(7)

The right-hand side is the nominal unit cost of R & D. V represents the value of the patent, which is given by the discounted stream of the monopoly profit:

where R is the nominal interest rate. Differentiating both sides with respect to time, t, yields the following no-arbitrage condition:

(8)

2.5. Households

Household j possesses nominal money balances, , and share of the monopoly firms,. The share yields returns at rate R. Thus, the budget constraint of household is given by

where is the nominal assets of household j, is labor supplied elastically by household j, and is consumption of household j. is nominal transfer income from the financial authorities in a lump-sum fashion. The final goods market clears

when. We can rewrite the budget constraint in real terms as

where is the real interest rate, is the inflation rate, is real money balances, and is the stock of assets in real terms.

Household j obtains utility from consumption, , and real money balances, , and it encounters disutility from the labor supply, , and wage negotiations. Thus, the instantaneous utility function of household j is

where is the elasticity of the marginal disutility of the labor supply. denotes the scale of the nominal wage adjustment cost from wage negotiations and ⁴. If, the nominal wage is flexible; however, if, the nominal wage is sticky. and denote the utility weights on real money balances and labor supply, respectively.

Summarizing the above, household j faces the following dynamical optimization problem:

where is the subjective discount rate. Since all households behave symme- trically according to the same equations, , , , , and hold. When, the solution to the optimization problem above is cha- racterized by the Euler equation and the wage version of the NKPC, as follows:

(9)

where is real money balances for the entire economy. The transversality condition for the households is given by.

On the other hand, when the following equation holds instead of the NKPC (9):

(10)

2.6. Money Growth

Financial authorities are assumed to change money supply, M, at a constant rate. That is, the financial policy rule is given by. Therefore, holds. All seignorage is transfered to households; that is,.

3. Steady State

When the nominal wage is sticky (), and the positive composite labor is allocated to R & D at any time () the equilibrium path is characterized by the transversality condition and the following differential equations:

(11)

(12)

(13)

where and

(14)

When R, , and are given, we obtain the, , and as follows:

(15)

(16)

(17)

and were defined as and.

3.1. Balanced Growth Path

If the law of motion (11) through (13) has fixed points, they are derived as follows:

where is the increasing function of defined as. is determined by the following wage version of the long-run Phillips curve:

(18)

The steady-state values of and are

(19)

However, to guarantee that is positive, must be greater than.

If it is the case that, at this fixed point y and N grow at constant rates. That is, the economy achieves balanced growth. We shall define this steady state as the balanced growth path (BGP). From (4) and (6), the balanced-growth rate of output is derived as

. From (17), the inflation rate along the BGP is given by the difference between the money growth rate and the long-run growth rate; that is,.

3.2. Natural Employment Level

We refer to the output and employment level in the flexible-price economy (i.e., when) as the natural output level and the natural employment level. The employment gap is the difference between the actual and natural employment levels. In the flexible-price economy, the employment level, l, is characterized by (10) instead of

NKPC (9). Then, substituting (4), (19), and into (10), we obtain the natural employment level along the BGP, , as the root of the following implicit function:

3.3. Existence and Uniqueness of the Balanced Growth Path

3.3.1. Case of Non-Negative Money Growth

When () belongs to, the long-run Phillips curve (18) is upward sloping on a -plane as shown in Figure 1. Note that the horizontal axis measures the employment level instead of the unemployment rate or the employment gap since we focus on the employment level rather than the unemployment rate in this study. Therefore, the usual Phillips curve is flipped backward in Figure 1.

Figure 1. The long-run Phillips curve at the BGP (for).

When is given, the BGP level of employment, , is uniquely determined according to the long-run Phillips curve. However, for a small value of, the root of the equation, , is smaller than; it is inappropriate for the BGP value. This threshold is given by

These results may be summarized as follows:

Proposition 1. Let. If and only if, a unique BGP, , exists. On the other hand, if, there is no BGP.

When the R & D sector is sufficiently productive and the parameters satisfy

holds; thus, always holds. In this case, when the financial authorities apply a monetary policy with, holds and the employment gap caused by nominal wage stickiness is eliminated.

If, the existence of the BGP requires that the money growth rate, , is sufficiently high. When is small and the BGP does not exist, there is only the no- growth steady state mentioned below.

3.3.2. Case Allowing Money Contraction

Some algebra shows that, and. Therefore, when we allow a negative value of, is convex and a unimodal form through the origin as shown in Figure 2. However, is bounded by to guarantee that the BGP value of the nominal interest rate, , is positive.

When the parameters satisfy

(a) (b)(c) (d)

Figure 2. The long-run Phillips curve at the BGP (for). (a); (b); (c) [; (d).

[see Figure 2(a) and Figure 2(b)]. In contrast, for, holds [see Figure 2(c) and Figure 2(d)]. Moreover, if the parameters satisfy

is greater than [see Figure 2(a) and Figure 2(c)]. For, holds [see Figure 2(b) and Figure 2(d)]⁵. To sum up these findings, we can see four cases as shown in Figures 2(a)-(d)⁶.

At first, in the cases of Figure 2(b) and Figure 2(d), has a unique root such that for all. That is, a unique BGP exists for all possible money growth rates.

In the case of Figure 2(a), is again a necessary and sufficient condition for the existence of a unique BGP. That is, sufficiently high rates of money growth are required to achieve sustained economic growth.

The following proposition summarizes the above properties.

Proposition 2.

1. If the parameters satisfy, a unique BGP, , exists for all.

2. Let the parameters satisfy. If and only if, a unique BGP, , exists. In contrast, if, there is no BGP.

On the other hand, in the case of Figure 2(c), it is possible that has dual roots, and, which belong to under a contractionary monetary policy⁷. To put it more precisely, we can state the following proposition.

Proposition 3. Let hold. For, a unique BGP, , exists. For close enough to, dual BGPs, and, exist.

Letting, we obtain. Therefore, when the money growth rate, , is smaller than and belongs to the neighborhood of, BGPs with a high and low growth rate coexist. Our model has no mechanism to choose between them. That is, global indeterminacy arises. The behavior of the economy is determined by agents’ expectations. If the minimum value of is greater than, by de- creasing toward, a saddle-node bifurcation will occur and the BGPs will vanish.

The arguments of Propositions 1 through 3 are summarized in Table 1 for the case of.

3.4. Money Growth, Inflation, and Economic Growth

Let a unique BGP exist. Then, we obtain the following proposition.

Proposition 4. Let hold and a unique BGP exists. In response to a permanent increase in the money growth rate, , the economy experiences greater employment and faster economic growth along the unique BGP.

This proposition can be proved as follows. As shown in Figure 1 and Figure 2, when a unique BGP exists, lies on the upward-slope of the long-run Phillips curve. There-

Table 1. The existence and uniqueness of BGP ().

Note: “―” shows that no such combinations of parameters exist because.

fore, an increase in raises the BGP level of employment,. Since and, an increase in raises labor allocated to each sector⁸. As a result, since, the greater value of raises. That is, economic growth accelerates with money growth⁹.

Furthermore, consider the following two facts. First, the growth acceleration effect of money growth is attributed purely to nominal wage stickiness. A small value of diminishes the impact of money growth on employment and economic growth. In a flexible-price economy, a change in the money growth rate has no effect on employ- ment and economic growth. That is, money is super neutral¹⁰. Second, even if financial authorities add 1% to the money growth rate, the rise in the long-run inflation rate is smaller than 1% because of the rise in the long-run growth rate. That is, the impact of money growth on the long-run inflation rate is weakened by endogenizing growth. Moreover, for high productivity R & D, which is captured by large values of, the inflation rate might even decrease.

As for dual BGPs, we can prove the following proposition in a similar way to that of Proposition 4.

Proposition 5. Let dual BGPs exist. At the BGP with lower employment level, an increase in the money growth rate raises employment and the balanced-growth rate. Whereas, at the BGP with a higher employment level, an increase in the money growth rate depresses employment and the balanced-growth rate.

3.5. No-Growth Steady State

There exists a different steady state from the BGP at which no labor is allocated to R & D and long-run growth never occurs. We refer to such a steady state as the no-growth steady state. At the no-growth steady state, since the free-entry condition (7) does not hold with an equality, (14), (15), and (16) are not fulfilled, and and hold instead of them.

The value of each variable at this steady state is derived as follows:¹¹

If and only if, the no-growth steady state, , exists¹². When and there is no BGP, the no-growth steady state, , is a unique steady state of the economy. If two BGPs exist as shown in Proposition 3, there are three steady states in all, and global indeterminacy arises among them.

4. Conclusions

This study developed a R & D-based endogenous growth model by introducing money growth and a price adjustment process. This study assumed that nominal wage is adjusted stickily because of adjustment cost and derived the new Keynesian Phillips curve, under which money is not super neutral even in the long-run.

When the money growth rate is sufficiently high, the economy has a unique balanced growth path, and can sustain long-run positive growth based on sustained R & D. Fur- thermore, faster money growth brings greater employment and faster economic growth along a unique balanced growth path. In contrast, under some parameter restrictions, when the money growth rate is sufficiently low, there is no balanced growth path, and the economy is trapped in a no-growth steady state. These results suggest that money growth may be an important factor for long-run economic growth.

To highlight the effect of nominal wage stickiness, this study adopted the money-in- utility-function approach, under which money is supernatural in a flexible-price eco- nomy. One interesting extension would be to analyze a model with another specifi- cation for money demand, for example cash-in-advance approach. In such case, the super neutrality of money may not hold even in a flexible-price economy, and the growth acceleration effect which is argued in this study might be weakened or strengthened. Such topic will be the subject of future research.

Acknowledgements

We thank the Editor and the referee for their comments. This paper is a part of the outcome of research performed under a Waseda University Grant for Special Research Projects (Project number: 2015B-014).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kocherlakota, N. (2016) Fragility of Purely Real Macroeconomic Models. NBER Working Paper No. 21866.
[2]	Inoue, T. and Tsuzuki, E. (2011) A New Keynesian Model with Technological Change. Economics Letters, 110, 206-208. http://dx.doi.org/10.1016/j.econlet.2010.11.020
[3]	Tsuzuki, E. and Inoue, T. (2010) Policy Trade-Off in the Long Run: A New Keynesian Model with Technological Change and Money Growth. Economic Modeling, 27, 943-950. http://dx.doi.org/10.1016/j.econmod.2010.05.009
[4]	Marquis, M.H. and Reffett, K.L. (1991) Real Interest Rates and Endogenous Growth in a Monetary Economy. Economics Letters, 37, 105-109. http://dx.doi.org/10.1016/0165-1765(91)90115-2
[5]	Marquis, M.H. and Reffett, K.L. (1995) The Inflation Tax in a Convex Model of Equilibrium Growth. Economica, 62, 109-121. http://dx.doi.org/10.2307/2554778
[6]	Jones, L.E. and Manuelli, R.E. (1995) Growth and the Effects of Inflation. Journal of Economic Dynamics and Control, 19, 1405-1428. http://dx.doi.org/10.1016/0165-1889(94)00835-6
[7]	Pecorino, P. (1995) Inflation, Human Capital Accumulation and Long-Run Growth. Journal of Macroeconomics, 17, 533-542. http://dx.doi.org/10.1016/0164-0704(95)80067-0
[8]	Mino, K. (1997) Long-Run Effects of Monetary Expansion in a Two-Sector Model of Endogenous Growth. Journal of Macroeconomics, 19, 635-655. http://dx.doi.org/10.1016/S0164-0704(97)00034-7
[9]	Mino, K. and Shibata, A. (1995) Monetary Policy, Overlapping Generations, and Patterns of Growth. Economica, 62, 179-194. http://dx.doi.org/10.2307/2554902
[10]	Mino, K. and Shibata, A. (2000) Growth and Welfare Effects of Monetary Expansion in an Overlapping-Generations Economy. Japanese Economic Review, 51, 407-430. http://dx.doi.org/10.1111/1468-5876.00160
[11]	Annicchiarico, B., Pelloni, A. and Rossi, L. (2011) Endogenous Growth, Monetary Shocks and Nominal Rigidities. Economics Letters, 113, 103-107. http://dx.doi.org/10.1016/j.econlet.2011.06.009
[12]	Annicchiarico, B. and Rossi, L. (2013) Optimal Monetary Policy in a New Keynesian Model with Endogenous Growth. Journal of Macroeconomics, 38, 274-285. http://dx.doi.org/10.1016/j.jmacro.2013.10.001
[13]	Vaona, A. (2012) Inflation and Growth in the Long Run: A New Keynesian Theory and Further Semiparametric Evidence. Macroeconomic Dynamics, 16, 94-132. http://dx.doi.org/10.1017/s1365100510000453
[14]	Tsuzuki, E. and Inoue, T. (2011) Technological Change and Monetary Policy in a Sticky-Price Model. Research in Economics, 65, 180-194. http://dx.doi.org/10.1016/j.rie.2010.08.001
[15]	Fischer, S. (1993) The Role of Macroeconomic Factors in Growth. Journal of Monetary Economics, 32, 485-512. http://dx.doi.org/10.1016/0304-3932(93)90027-d
[16]	Barro, R.J. (1995) Inflation and Economic Growth. Annals of Economics and Finance, 14, 121-144.
[17]	Barro, R.J. (1996) Inflation and Growth. Federal Reserve Bank of St Louis Review, 78, 153-169.
[18]	Levine, R. and Zervos, S.J. (1993) What We Have Learned about Policy and Growth from Cross-Country Regressions? The American Economic Review Papers and Proceedings, 83, 426-430.
[19]	Ericsson, N.R., Irons, J.S. and Tryon, R.W. (2001) Output and Inflation in the Long Run. Journal of Applied Econometrics, 16, 241-253. http://dx.doi.org/10.1002/jae.614
[20]	Bruno, M. and Easterly, W. (1998) Inflation Crises and Long-Run Growth. Journal of Monetary Economics, 41, 3-26. http://dx.doi.org/10.1016/S0304-3932(97)00063-9
[21]	McCandless, J.G.T. and Weber, W.E. (1995) Some Monetary Facts. Federal Reserve Bank of Minneapolis Quarterly Review, 19, 2-11.
[22]	Aleskerov, F. and Alper, E.C. (2000) A Clustering Approach to Some Monetary Facts: A Long-Run Analysis of Cross-Country Data. Japanese Economic Review, 51, 555-567. http://dx.doi.org/10.1111/1468-5876.00170
[23]	Pollin, R. and Zhu, A. (2006) Inflation and Economic Growth: A Cross-Country Nonlinear Analysis. Journal of Post Keynesian Economics, 28, 593-614. http://dx.doi.org/10.2753/PKE0160-3477280404
[24]	Remer, S., Bick, A. and Nautz, D. (2013) Inflation and Growth: New Evidence from a Dynamic Panel Threshold Analysis. Empirical Economics, 44, 861-878. http://dx.doi.org/10.1007/s00181-012-0553-9
[25]	Villavicencio, A. and Mignon, V. (2011) On the Impact of Inflation on Output Growth: Does the Level of Inflation Matter? Journal of Macroeconomics, 33, 455-464. http://dx.doi.org/10.1016/j.jmacro.2011.02.003
[26]	Lee, C.-C. and Wong, S.Y. (2005) Inflationary Threshold Effects in the Relationship between Financial Development and Economic Growth: Evidence from Taiwan and Japan. Journal of Economic Development, 30, 49-69.
[27]	Grossman, G.M. and Helpman, E. (1991) Innovation and Growth in the Global Economy. MIT Press, Cambridge.
[28]	Rotemberg, J.J. (1982) Sticky Prices in the United States. Journal of Political Economy, 90, 1187-1211. http://dx.doi.org/10.1086/261117