Frequency Domain Approach for Face Recognition Using Optical Vanderlugt Filters ()


1. Introduction
When we talk to someone, we usually look at his face. Face recognition not only plays an important role in social interactions but also is crucial for security check and human machine interface. In comparison with fingerprint or iris data which need complex devices, face pictures can easily and interactively be gathered by a simple camera. Therefore face recognition has advantages over other biometrics. It has been a challenging subject for over 50 years and yet many researchers are investigating on methods to solve its complicated problems.
Filtering images for image processing purposes involving face recognition has been investigated in two main categories. One is to use optical correlators in which face images are considered as a whole and the other is to use digital methods in which pixel computations under the concept of digital image processing are concerned [1] [2]. Using optical filters to measure similarity between images is being considered for decades [3]. Since optical filtering basically rely on using spatial Fourier transform of images in frequency domain, practically it can be achieved by use of simple optical elements such as converging lenses [4]. Furthermore, regarding to the parallel nature of optical processing; since light waves travel in parallel, all the information of an image can be searched at the speed of light and it can be considered as real-time processing.
A review on optical image processing using Vanderlugt filtering and its calculations which are the basics of our investigation is presented in Section 2. Section 3 will cover a description on the dataset which we used and our investigation on it with the Vanderlugt correlator. Conclusion is presented in Section 4.
2. A Review on Optical Image Processing Using Vanderlugt Filters
Several methods for optical image processing exist which rely on similar concepts. One of the basic methods is to process images by means of Vanderlugt spatial filtering [5]. Based on that, 2-D Fourier transform information of an object can be recorded on a photo-sensitive film. Using Vanderlugt filtering and a correlation setup called 4f or Frequency Plane Optical Correlator; FPC, optical image processing and pattern recognition in images can be accomplished.
2.1. 4f Correlator Setup
A simple and effective setup for optical image processing called 4f setup is illustrated in Figure 1. This system provides the correlation between two images. One image is placed on the input plane and the filtered form of another image is settled in the Fourier plane position. As can be seen, a laser beam passes through the first image and the first optic lens and shapes Fourier transformed form of the first image on the Fourier plane. Vanderlugt filter of the second image which contains its frequency domain information interferes with the Fourier transformed of the first image. As the interference passes through the second optical lens, practically an inverse Fourier transform is applied. Therefore the inverse Fourier transform of the multiplication of Vanderlugt filter and input image in the frequency domain will form on the output plane regarded as the correlation between the two images. By sensing the intensity of the correlation and comparing it to the auto-correlation of images, the similarity between two images can be measured [6].
2.2. Providing Vanderlugt Filter of an Image
Figure 2 shows a schematic setup to synthesize spatial frequency Vanderlugt filter of an image on a film. The L1 lens emit parallel light on P1 plane which has the image on it with the spatial impulse response of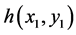 . When the image light passes through L2 lens, in the distance of focal length of L2, spatial Fourier transform of
. When the image light passes through L2 lens, in the distance of focal length of L2, spatial Fourier transform of
the image forms on the P2 plane. Therefore we will have  on the P2 plane. A photo-sensitive
on the P2 plane. A photo-sensitive
plane can be substituted instead of P2. Also, the P prism, directly guides a part of the source light towards the P2 plane, thus this light and the light coming from the L2 lens interfere on the P2 plane. So the interference of source light and the Fourier transform of the image will be recorded on the film placed instead of the P2 plane.
If the tilted plane wave incident from the prism produces a field distribution at the P2 plane as below:
at the P2 plane as below:
![]()
Figure 2. Vanderlugt filter synthesis setup [4].
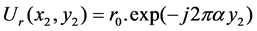 (1)
(1)
where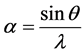 , then the interference model on P2 will be as:
, then the interference model on P2 will be as:
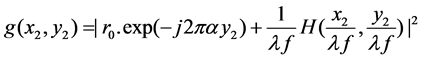 (2)
(2)
Since a photo-sensitive film is only sensitive to the intensity of light, the model is squared in the Equation (2). By manipulating the Equation (2), 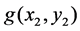 will be as:
will be as:
 (3)
(3)
As the final stage for the synthesis of the image’s spatial frequency Vanderlugt filter, the film would record a transparent picture where its amplitude;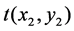 , is related to the intensity of the light coming from both the image and the source.
, is related to the intensity of the light coming from both the image and the source.
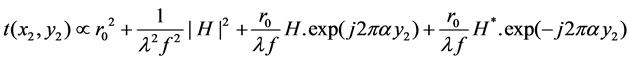 (4)
(4)
The third term in Equation (4) is exactly the Fourier transform of the impulse response of the image and thus can be used for optical processing in spatial frequency domain purposes.
2.3. Image Processing by Means of the Vanderlugt Filter
Synthesized Vanderlugt filter can be replaced by the Fourier plane of Figure 1. If the input image to be filtered is shown by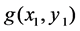 , its spatial frequency distribution will be equal to
, its spatial frequency distribution will be equal to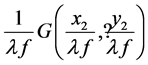 . Regarding to the Equation (4), optical signal received on the Fourier plane of the 4f correlator depicted in Figure 1 will be as:
. Regarding to the Equation (4), optical signal received on the Fourier plane of the 4f correlator depicted in Figure 1 will be as:
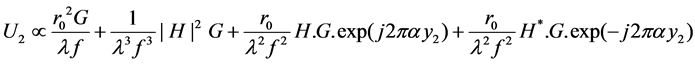 (5)
(5)
 is the multiplication of the Vanderlugt filter and the Fourier transform of the input image in the frequency domain. When this interference passes through the second lens of the 4f correlator, after traveling as far as the focal length of the lens, inverse Fourier transform is applied and
is the multiplication of the Vanderlugt filter and the Fourier transform of the input image in the frequency domain. When this interference passes through the second lens of the 4f correlator, after traveling as far as the focal length of the lens, inverse Fourier transform is applied and ![]() will form on the output plane.
will form on the output plane.
![]() (6)
(6)
The third term of the Equation (6) is the convolution between ![]() and
and ![]() which will occur at an area centered at
which will occur at an area centered at ![]() on the output plane. The fourth term can be written as,
on the output plane. The fourth term can be written as,
![]() (7)
(7)
which is the correlation between ![]() and
and ![]() which will occur at an area centered at
which will occur at an area centered at ![]() on the output plane.
on the output plane.
Thus, if the light source makes the sufficiently large angle with the P2 plane during the Vanderlugt filter synthesis, the convolution and correlation areas would be far from each other enough on the output plane of the 4f correlator. This leads to the possibility of spatial high-pass filtering the output plane in order to achieve to the correlation and convolution between the input image and the Vanderlugt filter separately.
Note that spatial high-pass filtering means to allow passing part of the optical signal which is away from the center of the plane. Also note that the first and the second terms of the Equation (6) which occur around the center of the output plane, have the least effect on the desired output and as they will be spatially filtered by the high-pass filter, they will be neglected for the simulation as well.
In Figure 3, the output plane of the 4f correlator is illustrated. The place of the convolution and the cross correlation can be seen as described.
If the maximum spatial width of ![]() and
and ![]() is regarded as
is regarded as ![]() and
and ![]() respectively, then the possible maximum value of the discussed four terms will be as below:
respectively, then the possible maximum value of the discussed four terms will be as below:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]()
Figure 3. Locations of the correlator output terms [4].
![]() (11)
(11)
So to be able to separate the four terms on the output plane spatially, ![]() and
and ![]() should meet the limitations of Equation (12) and Equation (13).
should meet the limitations of Equation (12) and Equation (13).
![]() (12)
(12)
![]() (13)
(13)
It is of significant importance to consider that since naturally in a 4f setup the spatial impulse response of a desired image will be computed and recorded automatically with the speed of light, there will be no need for complex and time consuming computations as in digital systems is required. More important, the Vanderlugt filter records both the amplitude and the phase of a Fourier transformed image on the same film with high resolution so there will be no need to record the amplitude and the phase information separately.
3. Our Investigation
In year 2002 an investigation was done on English alphabet recognition at our Photonics Research Laboratory; PRL, and the designed system was successfully implemented as a hybrid optical-digital processor with simple optical elements and a personal computer [7]. It motivated us to simulate a similar process for face recognition which demands more precise calculations due to the more complex nature of face images. The investigation is done on the “ORL face database” collected from 40 subjects each with 10 different variations in their pose [8].
An overview of the data set is presented in Figure 4.
The problem was to recognize an input subject among the 400 images of different 40 people using the Vanderlugt filtering and 4f correlator. First a database of Vanderlugt filters of all the images in the dataset had to be created. This has been done by numerically implementing the Equation (2) for the MATLAB software. This implementation may be a little tricky due to the high sensitivity of discrimination between different subjects’ Vanderlugt filters to the accuracy of the implementation. All the parameters and constants should be considered precisely to obtain a resolution near the real optical setup; otherwise the correlation simulation will fail. In Figure 5 two images from ORL data set and their calculated Vanderlugt filters are presented.
The next step is to apply each intended face image to the 4f correlator and correlate it with all the Vanderlugt filters of the images in the data set. For this means, Fourier transform of each of the input images is multiplied by the Vanderlugt filters and the result are inverse Fourier transformed to obtain the optical correlation on the
![]()
Figure 4. Part of the ORL dataset which was used [8].
output plane. Now the maximum value of the output plane is used as a measure of similarity. Thus the more this value is, the more the input image should be similar to that Vanderlugt filter.
First we have simulated this setup for all the 400 pictures and our system recognized the input image nearly errorless and with about 100% accuracy. It means that the input image exactly matches with its Vanderlugt filter as they have the highest optical correlation among all. In Figure 6 bar charts for six subjects are presented which show the normalized optical correlation between the first images of six different subjects from the dataset and all the 400 Vanderlugt filters of the whole dataset. As can be conducted, the correlation of the input image with its respective Vanderlugt filter is the highest among all with a considerable difference to others, leading to a high confidence on the recognition output. Second peak and next high numbers are for the same subject with different positions. Although some of them failed to match better than other subjects with the input image. In Figure 6, each 10 bars relate to different positions of an individual subject.
![]()
Figure 5. Subject 1 and its Vanderlugt in the above row, subject 6 and its Vanderlugt in the bottom row.
![]()
Figure 6. The optical correlation between the first image of six subjects and the Vanderlugt filters for all the 400 ORL face.
4. Conclusion
Face recognition problems are divided in two major subsets as face identification (identifying a person among a set of people) and face verification (verifying that a person is who he claims). In our survey our focus was on face identification. As showed in previous sections, processing images using a real optical setup especially for correlation is faster than the digital processers as processes here take place at the speed of light. This approach can be highly beneficial to use in security check stations, e.g. in airports. A database of suspects Vanderlugt filters can be made and for each in sufficient different positions and the correlation will immediately be ready. Although this approach can fail when the subject’s pose difference increases, varieties of subjects’ poses can be added to the Vanderlugt database without losing the speed due to the real-time nature of this optical setup. Furthermore, as security check usually takes place in controlled situations, worries about the pose difference of the subject and its image in the Vanderlugt data base can be neglected and identification can be achieved with nearly 100% accuracy. To expand the usage of this approach and to add more flexibility to the situations in which it will work accurate, an optical correlator can be combined with a digital processor. The digital processor can help in applying preprocessing on the input image in order to eliminate spatial and illumination noises and occlusions which can affect the optical correlator output quality.