Statistical Transform of Signal Field with ASE Noise through a Fiber Amplifier ()
1. Introduction
The statistical model of phase noise induced by the interplay between amplifier spontaneous emission (ASE) noise and fiber Kerr nonlinearity, is extensively studied during the last decade. The probability density function (p.d.f.) of ASE noise + signal field is necessary to analyze the noise properties and evaluate the system performances.
By converting a Cartesian into a polar description, the nonlinear phase noise (NPN) (the additive component of ASE noise) was identified to be nearly Gaussian [1]. Then in [2], by linearizing the interaction between a signal and noise in the limit of a distributed system, authors evaluated the closed Gaussian form ASE power spectral density. Even if the received ASE was non-stationary in time due to pulse shape and modulation, they showed that it could be approximated by an equivalent stationary process, as if the signal was continuous wave (CW). Such a method avoided the calculation of nonlinear phase statistics. The CW-equivalent ASE model was also used to evaluate bit-error-rate by an extension of the known Karhunen-Loéve method. Additionally, the combined regular-logarithmic perturbation model was used to derive the basic propagation equations of ASE noise in amplified multi-span optical systems [3]. Also, in situations that no analytical theory was available for the dispersion and nonlinearity managed transmissions, the important sample algorithms performed a direct computation of the random optical soliton phase statistical distribution under the action of nonlinear phase noise [4].
But by the experimental observation and performance study of the differential phase-shift-keying transmission systems [5] [6], the results showed that the p.d.f. of nonlinear phase noise deviated from the Gaussian distribution, and this characteristic negated the benefit of a balanced receiver [7]. Thus, the calculation of nonlinear phase noise had to turn back to the original theory [8] and this distributed model was described as the transform of stochastic Wiener process [9]. Firstly, it was given as a summation from the contribution of many fiber spans. If the number of fiber spans was very large, the summation was replaced by an integration. Several years ago, an approximate but analytical treatment of the statistical properties of the NPN of an isolated RZ pulse was presented and it revealed that the variance of NPN in a dispersion-managed fiber-optics link might be reduced by properly decreasing the duty cycle of an RZ pulse [10].
Taking the dispersion effect into account, the p.d.f. of signal pulse with nonlinear phase noise was broadened and the broadening was asymmetrical with respect to the mean nonlinear phase shift [11]. Based on the assumption that phase noise was linearly approximated, T. Pollet considered the BER performance in OFDM system in the presence of phase noise and frequency offset [12]. The nonlinear stochastic differential equation was also developed to approximate phase noise in oscillators. E. Costa and S. Pupolin studied M-QAM-OFDM system performance in the presence of a nonlinear amplifier and phase noise [13]. They approximated the phase noise linearly. A more detailed analysis was still required to study phase noise’s influence. So in [14], a nonlinear approximation about phase noise including the second order term of phase noise was proposed.
In this paper, the probability transform is studied when ASE noise +signal field pass through a span of transmission fiber and a fiber amplifier where ASE noise is generated and described by a delta (δ)-function. The dispersion effect of fiber is taken into account, so the statistical properties of the field are nonstationary. In the amplifier, ASE noise is generated, and thus based on the birth theory of stochastic, the field’s statistical transform is established and the probability distribution through 50 km nonzero-dispersion-shifted fiber (NZDSF), a dispersion compensation grating and an erbium-doped fiber amplifier (EDFA), are obtained.
2. Theory
The optical field envelope in an amplified transmission system is governed by the nonlinear Schrodinger(NLS) equation [15]
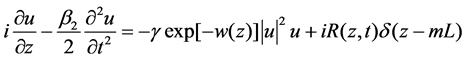(1)
where 
is the dispersion profile, 
is the nonlinear coefficient,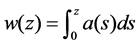 
and 
is the fiber loss profile.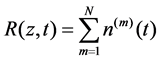 
represents the noise field due to an amplification. 
is the amplifier location.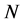 
is the number of amplifiers and 
is the noise field due to the amplifier located at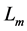
. The mean and autocorrelation functions of the noise field are given by
,
.
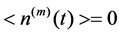where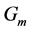 
is the gain of the amplifier, 
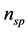is the spontaneous noise factor, 
is the Plank’s constant and 
is the mean optical carrier frequency.
Disregard the stochastic item in (1), we can calculate the optical field without ASE noise item by the split-step method [16]
![]()
(2)
Now, (1) can be written as
![]()
(3)
Assume ![]()
is the arbitrary function of the signal + noise field and ![]()
has a probability density ![]()
[7] [17]
![]()
(4)
where ![]()
refers to the Weiner process.
![]()
(5)
According to the property of ![]()
![]()
(6)
we get the generalized Fokker-Plank equation describing the signal field with ASE noise
![]()
(7)
In particular, the isolated system (![]()
and![]()
) produces a stationary solution in the form [17]
![]()
(8)
We assume the transient solution (only![]()
) is the form
![]()
(9)
![]()
(10)
![]()
(11)
![]()
(12)
![]()
(13)
![]()
is determined by the launched pulse and![]()
, so![]()
.
Taking the ASE noise as a perturbation item, we now try to solve the perturbed Fokker-Planck Equation (8) [8] [18]
![]()
(14)
![]()
(15)
Its eigenvalue and eigenfunction can be expanded as
![]()
(16)
![]()
(17)
Finally, comparing the terms ![]()
in both sides, we get
![]()
(18)
![]()
(19)
(17) and (18) can be written as
![]()
![]()
(20)
![]()
(21)
![]()
(22)
![]()
(23)
The item of p in (23) is definite because of the orthogonality and normalization of (13). Also, the coefficients bp and Yn are determined by the input field of the amplifier. Note that, this model requires that the first order differential of ![]()
is continuity, otherwise, the Green function of Equation (22) has no meaning.
3. Discussion
In this section, we will simulate the p.d.f. of the ASE noise+ signal field after transmitted in NZDSF, grating and an amplifier link such as Figure 1. The measured points a, b and c correspond to the sub-figures a, b and c in Figure 2, respectively.
Fibers parameters are: a = 0.21 (dB/km), γ = 2.2 (/km/W), D = 4.4 (ps/nm/km). The pulse is:
![]()
![]()
mW, ![]()
and ![]()
ps, ![]()
is the half-width at 1/e intensity point.
There are frequency offsets in the p.d.f. when the dispersion and nonlinear effects in transmission fiber are taken into account and they cannot be dissipated by dispersion compensation. Figure 2(a) and Figure 2(b) present these properties. The probability distribution after NZDSF is based on (9) and (10) and that after the amplifier is according to (20) and (21) (with ASE noise item). The probability transform passing through the dispersion compensation grating is from [19] by the matrix
![]()
where D is the compensation dispersion supplied by grating.
The sideband induced by dispersion and nonlinear effects is not transient and it exists at a certain probability. From the mathematical formula, the solution (11) is the Hermite polynomial and it is a series of vibration functions. When they add together several times, the side bands occur but still with a lot of chances, they are located neither in the field nor in the sideband regions. These are determined by the coefficient ![]()
(the ASE noise
![]()
Figure 1. Schematic of the simulation setup.
+ signal field) and similar to the case of [18] by mixing the Gauss p.d.f. The amplifier, amplifying the signal and generating ASE noise, will result in relative decrease of the non-field and non-sideband probability but it can’t change the impact of dispersion and nonlinear effects on field statistical distribution (Figure 1(c)).
Phase shifts caused by the nonlinear effect are also consistent with [20] and as its authors had expected that, if the dispersion effect was taken into account, there were the asymmetric modulation side-bands occurring.
It is most likely that this figure can’t clearly show the impact of local ASE noise (generated in EDFA). So, in Figure 3, we extract the distribution brought by the generated ASE noise.
![]()
![]()
(a) (b)
Figure 3. The probability distribution (a) real value; (b) image value brought by the generated. ASE noise at the wavelength of signal.
4. Conclusion
Therefore, in the fiber + dispersion grating + amplifier transmission systems, the evaluation about the statistical transform of signal + ASE noise field shows that the frequency offset of the field’s probability distribution induced by dispersion and nonlinear effects in transmission fiber cannot be dissipated by dispersion compensation and the ASE noise generated in the amplifier is a perturbation item and has weak impact on the field’s p.d.f., but it accelerates the field’s frequency offset.