Is the Two-Color Method Superior to Empirical Equations in Refractive Index Compensation? ()


1. Introduction
Meter, the unit of length, is defined in vacuum. However, measurements of length are often carried out in air, which presents some problems. Let us assume that we want to compare two geometric distances 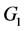 and
and . These two distances are measured in air as
. These two distances are measured in air as 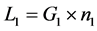 and
and , where
, where 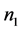 and
and  are the refractive index of air (RIA). In the absence of a relationship between
are the refractive index of air (RIA). In the absence of a relationship between 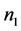 and
and , it is not possible to determine which of
, it is not possible to determine which of 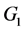 and
and  is greater only by judging the magnitude relationship between
is greater only by judging the magnitude relationship between  and
and . To solve this problem, the influence of RIA must be eliminated.
. To solve this problem, the influence of RIA must be eliminated.
One approach to obtaining the value of RIA is to use empirical equations [1]-[4]. With n obtained, an estimate of the geometric distance 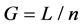 can be calculated. The estimated geometric distance can be used for comparison. The empirical equations are used to compensate for the RIA under two assumptions. First, environmental parameters (namely, temperature, pressure, and humidity) can be measured. Second, a measured environmental parameter is a good reproduction of that parameter along the optical path, meaning that a measured environmental parameter is an average value over time and space. In other words, both the spatial distribution of environmental parameters and the time-delay of measurement equipment can be ignored. These assumptions are valid only if the measurement is performed in a closed environment (e.g., a well-controlled laboratory or underground tunnel with limited variation in environmental parameters).
can be calculated. The estimated geometric distance can be used for comparison. The empirical equations are used to compensate for the RIA under two assumptions. First, environmental parameters (namely, temperature, pressure, and humidity) can be measured. Second, a measured environmental parameter is a good reproduction of that parameter along the optical path, meaning that a measured environmental parameter is an average value over time and space. In other words, both the spatial distribution of environmental parameters and the time-delay of measurement equipment can be ignored. These assumptions are valid only if the measurement is performed in a closed environment (e.g., a well-controlled laboratory or underground tunnel with limited variation in environmental parameters).
Another approach to suppressing the influence of RIA is to apply the two-color method, which was first proposed by Bender and Owens [5] to compensate for the inhomogeneous disturbances of the RIA in an open environment. The core concept of the two-color method is to use a measured length difference between two colors (frequencies) to render length measurements less sensitive to changes in the RIA.
Recently, high-precision length measurements based on fem to second optical frequency comb (FOFC) have been carried out (e.g., [6] [7]). To compensate for the RIA, FOFC-based RIA measurements [8] [9] and FOFC- based two-color method experiments [10]-[12] have also been performed. Minoshima’s group performed a two- color method experiment in a well-controlled environment and found an agreement between RIA compensation based on the empirical equations and that of two-color method with a standard deviation of 3.8 × 10−11 throughout hours [13]. They also suggested that the accuracy provided by the empirical equations may be improved by the two-color method.
One question arises naturally: theoretically, is the two-color method superior to the empirical equations in RIA compensation? We employed a numerical approach to investigate this possibility.
2. Methods
2.1. Refraction Index Compensation by Empirical Equations
The distance between two points measured in air is an optical distance . An estimate of the geometric distance
. An estimate of the geometric distance 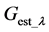 in vacuum and the optical distance has the following relationship.
in vacuum and the optical distance has the following relationship.
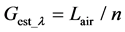 (1)
(1)
where n represents the RIA. By applying the law of propagation of uncertainty [14] [15] to Equation (1), we obtain the uncertainty of length in vacuum.
![]() (2)
(2)
where ![]() denotes the uncertainty of variable x. The first and second terms of the right-hand side of Equation (2) are the uncertainty due to the refractive index and the length measurement, respectively. These two are defined as follows, respectively.
denotes the uncertainty of variable x. The first and second terms of the right-hand side of Equation (2) are the uncertainty due to the refractive index and the length measurement, respectively. These two are defined as follows, respectively.
![]() (3)
(3)
![]() (4)
(4)
The uncertainty of refractive index can be evaluated by the following equation [16] [17].
![]() (5)
(5)
where![]() ,
, ![]() , and
, and ![]() are the uncertainties of the instrument for measuring temperature T, barometric pressure P, and humidity H, respectively.
are the uncertainties of the instrument for measuring temperature T, barometric pressure P, and humidity H, respectively.![]() ,
, ![]() , and
, and ![]() are sensitivity coefficients and defined as follows.
are sensitivity coefficients and defined as follows.
![]() (6)
(6)
where ![]() is the derivative of function
is the derivative of function ![]() at
at![]() . The definitions are similar for
. The definitions are similar for ![]() and
and![]() .
.
2.2. Refraction Index Compensation by Two-Color Method
The distances between two points measured in air by using different wavelengths are optical distances ![]() and
and![]() . An estimate of the geometric distance
. An estimate of the geometric distance ![]() from these two optical distances can be obtained as follows:
from these two optical distances can be obtained as follows:
![]() (7)
(7)
where A is the so-called A-factor defined as
![]() (8)
(8)
Equation (7) can be rewritten as follows.
![]() (9)
(9)
By applying the law of propagation of uncertainty to Equation (9), we have
![]() (10)
(10)
The uncertainties of the first and second terms of the right-hand side of Equation (10) are, respectively,
![]() (11)
(11)
![]() (12)
(12)
Because we have![]() , Equation (12) can be rewritten as follows.
, Equation (12) can be rewritten as follows.
![]() (13)
(13)
By substituting Equations (11) and (13) into Equation (10), we obtain
![]() (14)
(14)
The first and third terms of the right-hand side of Equation (14) are the uncertainty due to the A-factor, and the second and fourth terms are the uncertainty due to the length measurement. These two are defined as follows, respectively.
![]() (15)
(15)
![]() (16)
(16)
The uncertainty of A-factor is as follows.
![]() (17)
(17)
where![]() ,
, ![]() , and
, and ![]() are the sensitivity coefficients of the A-factor and are defined as follows.
are the sensitivity coefficients of the A-factor and are defined as follows.
![]() (18)
(18)
where ![]() is the derivative of function
is the derivative of function ![]() at
at![]() . The definitions are similar for
. The definitions are similar for ![]() and
and![]() .
.
2.3. Comparison of Empirical Equations and Two-Color Method
In Equation (4), the uncertainty due to the length measurement is multiplied by the factor![]() . In Equation (16), the uncertainty due to the length measurement is multiplied by two factors,
. In Equation (16), the uncertainty due to the length measurement is multiplied by two factors, ![]() and
and![]() . Normally, their orders are several tens. If the two wavelengths used in the two-color method are 780 nm and 1560 nm, then
. Normally, their orders are several tens. If the two wavelengths used in the two-color method are 780 nm and 1560 nm, then ![]() and
and![]() . By comparing the magnitudes of Equation (4) and Equation (16), we understand that only when the condition
. By comparing the magnitudes of Equation (4) and Equation (16), we understand that only when the condition
![]() (19)
(19)
is satisfied, the two-color method can be shown to obtain measurements with a smaller error than that of the empirical equations. We performed numerical calculations to check whether Equation (19) is feasible.
3. Numerical Calculations
We used the following parameters for simulation. By referring to Ref. [18], we employed 780.0 nm and 1560.0 nm as the two wavelengths. We used the equations for the phase refractive index given in Ref. [4]. Because of the limit on the length of this paper, we only considered the Edlén empirical equations in this study. In the Edlén empirical equations [2]-[4], the RIA can be derived from the wavelength in vacuum![]() , temperature T, barometric pressure P, and humidity H as
, temperature T, barometric pressure P, and humidity H as![]() . The formula used to perform the calculations can be easily accessed via the internet [4]. In the following, we only consider the phase refractive index. The group refractive index can be treated in the same way.
. The formula used to perform the calculations can be easily accessed via the internet [4]. In the following, we only consider the phase refractive index. The group refractive index can be treated in the same way.
On the basis of Equations (6) and (18), we calculated the change in the sensitivity coefficients when environmental parameters change in a realistic range (T ∊ [10, 30] ˚C, P ∊ [90,115] kPa, H = 0%). The calculations of the derivative of each refractive index have been validated in Ref. [19]. The same procedure was used in this study for calculating the derivative of the A-factor. After obtaining an expression for the sensitivity coefficients by substituting numerical values, the values of sensitivity coefficients were calculated.
As shown in Figure 1, when ![]() = 0%, the sensitivity coefficient of the A-factor is smaller than that of the refractive indices. This result, i.e., the A-factor can be considered as a function of just two wavelengths only when the humidity is 0%, is consistent with the results of previous studies [10] [11] [13] [20]-[24].
= 0%, the sensitivity coefficient of the A-factor is smaller than that of the refractive indices. This result, i.e., the A-factor can be considered as a function of just two wavelengths only when the humidity is 0%, is consistent with the results of previous studies [10] [11] [13] [20]-[24].
On the basis of Equations (3) and (15), we calculated the uncertainties due to the A-factor and refractive indices, respectively. The geometric distance G was set to 1 m. We assumed that ![]() and
and ![]() on the basis of using a thermometer (Testo 735, Testo) and a barometer (VR-18, Sunoh), respectively. These two are commercially available for us.
on the basis of using a thermometer (Testo 735, Testo) and a barometer (VR-18, Sunoh), respectively. These two are commercially available for us.
Figure 2 shows that![]() . This result means that in a 0% humidity environment, the two- color method has potential to provide greater measurement accuracy than the empirical equations. Note that the orders of values shown in Figure 2 were affected by the sensitivity coefficients of environmental parameters and the uncertainties of the instrument for measuring environmental parameters. A detailed uncertainty analysis in an environment where the humidity is not 0% will be reported in another paper.
. This result means that in a 0% humidity environment, the two- color method has potential to provide greater measurement accuracy than the empirical equations. Note that the orders of values shown in Figure 2 were affected by the sensitivity coefficients of environmental parameters and the uncertainties of the instrument for measuring environmental parameters. A detailed uncertainty analysis in an environment where the humidity is not 0% will be reported in another paper.
4. Conclusion
We analyzed the uncertainties of length conversion based on the Edlén empirical equations and the two-color
![]() (a)
(a)![]() (b)
(b)
Figure 1. Change in sensitivity coefficients of A-factor and refractive indices with (a) temperature when P = 101.325 kPa and H = 0% and (b) pressure when T = 20˚C and H = 0%.
![]() (a)
(a)![]() (b)
(b)
Figure 2. Change in uncertainties due toA-factor and refractive indices with (a) temperature when P = 101.325 kPa and H = 0% and (b) pressure when T = 20˚C and H = 0%.
method, in which the uncertainties due to length measurement and refractive index compensation were decomposed. Using numerical calculations of sensitivity coefficients of the A-factor and refractive indices of the environmental parameters, we found for the first time that in a realistic environmental parameter range (T ∊ [10, 30] ˚C, P ∊ [90, 115] kPa, H = 0%), the uncertainty of the two-color method due to the A-factor was smaller than that of the empirical equations due to refractive indices. This result suggests that in a 0% humidity environment, the two-color method has potential to provide greater measurement accuracy than the empirical equations, with the cooperation of suppressing the uncertainties of length measurements (compared with uncertainties of refractive index compensation) to a negligible level. The findings of this study provide a better insight into the two- color method, and will create opportunities for further development of application of this method.
Acknowledgements
This research work was partially financially supported by a grant (R1501) from the Mitutoyo Association for Science and Technology.
NOTES
![]()
*Corresponding author.