The Accurate Mass Formulas of Leptons, Quarks, Gauge Bosons, the Higgs Boson, and Cosmic Rays ()
Received 21 July 2016; accepted 28 August 2016; published 31 August 2016

1. Introduction
According to Johan Hansson, one of the ten biggest unsolved problems in physics [1] is the incalculable particle masses of leptons, quarks, gauge bosons, and the Higgs boson. The Standard Model of particle physics contains the particles masses of leptons, quarks, and gauge bosons which cannot be calculated or predicted theoretically. From a theoretical point of view, the particle mass is a total unsolved problem and they might as well have been random numbers drawn from a hat. The repetition of leptons and quarks with increasing masses has also remained as unsolved problem. Max Jammer [2] concluded that nobody knows what particle masses really are. The mass parameters experimentally measured for elementary particles have no theoretical explanation whatsoever. From the vantage point of theory, the masses could just as well be a set of randomly generated numbers.
This paper provides a solution to the unsolved problem of particle masses. In this paper, all elementary particles and cosmic rays (the knees-ankles-toe) can be calculated accurately and predicted theoretically by the accurate mass formulas of leptons, quarks, gauge bosons, the Higgs boson, and cosmic rays by using only five known constants: the number (seven) of the extra spatial dimensions in the eleven-dimensional membrane, the mass of electron, the masses of Z and W bosons, and the fine structure constant. The calculated masses are in excellent agreements with the observed masses. For examples, the calculated masses of muon, top quark, pion, neutron, and the Higgs boson are 105.55 MeV, 175.4 GeV, 139.54 MeV, 939.43 MeV, and 126 GeV, respectively, in excellent agreements with the observed 105.65 MeV, 173.3 GeV, 139.57 MeV, 939.27 MeV, and 126 GeV, respectively. The theoretical base of the accurate mass formulas is the periodic table of elementary particles [3] - [6] . As the periodic table of elements is derived from atomic orbitals, the periodic table of elementary particles is derived from the seven principal mass dimensional orbitals and seven auxiliary mass dimensional orbitals. All elementary particles including leptons, quarks, gauge bosons, the Higgs boson, and cosmic rays can be placed in the periodic table of elementary particles.
The periodic table of elementary particles is derived from the computer simulation model of physical reality [7] which is the theory of everything [8] . We are living in a computer simulation to simulate physical reality which has the same computer simulation process as virtual reality (computer-simulated reality). The computer simulation process involves the digital representation of data, the mathematical computation of the digitized data in geometric formation and transformation in space-time, and the selective retention of events in a narrative. Conventional physics cannot explain physical reality clearly, while computer-simulated physics can explain physical reality clearly by using the computer simulation process consisting of the digital representation component, the mathematical computation component, and the selective retention component. The computer simulation model of physical reality provides the seven principal mass dimensional orbitals and seven auxiliary mass dimensional orbitals for the periodic table of elementary particles.
In Section 2, the periodic table of elementary particles is derived from the computer simulation of physical reality. Section 3 deals with the gauge boson mass formula and the cosmic ray mass formula. Section 4 explains the lepton mass formula and the quark mass formula. Section 5 describes the Higgs boson mass formula.
2. The Periodic Table of Elementary Particles
The periodic table of elementary particles is derived from the computer simulation model of physical reality consisting of the mathematical computation, digital representation, and selective retention components.
2.1. The Mathematical Computation Component
The geometry in the mathematic computation component for the computer simulation process is oscillating M-theory. M-theory with eleven-dimensional membrane is an extension of string theory with ten-dimensional string, in contrast to the observed 4D. In conventional M-theory, space-time dimensional number (D) is fixed. As a result, the observed 4D results from the compactization of the extra space dimensions in 11D M-theory, However, there is no experimental proof for compactized extra space dimensions, and there are numerous ways for the compactization of the extra space dimensions [9] . As described before [7] , the geometry for the mathematical computation is oscillating M-theory derived from oscillating membrane-string-particle whose space-time dimension number oscillates between 11D and 10D and between 10D and 4D dimension by dimension reversibly. There is no compactization. Matters in oscillating M-theory include 11D membrane (211) as membrane (denoted as 2 for 2 space dimensions) in 11D, 10D string (110) as string (denoted as 1 for 1 space dimension) in 10D, and variable D particle (04 to 11) as particle (denoted as 0 for 0 space dimension) in 4D to 11D.
As described previously [10] , the QVSL (quantum varying speed of light) transformation transforms both space- time dimension number (D) and mass dimension number (d). In the QVSL transformation, the decrease in the speed of light leads to the decrease in space-time dimension number and the increase of mass in terms of increasing mass dimension number from 4 to 10,
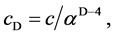 (1a)
(1a)
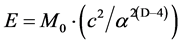 (1b)
(1b)
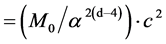 . (1c)
. (1c)
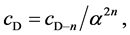 (1d)
(1d)
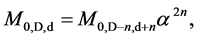 (1e)
(1e)
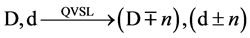 (1f)
(1f)
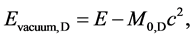 (1g)
(1g)
where cD is the quantized varying speed of light in space-time dimension number, D, from 4 to 10; c is the observed speed of light in the 4D space-time; α is the fine structure constant for electromagnetism, E is energy; M0 is rest mass; D is the space-time dimension number from 4 to 10; d is the mass dimension number from 4 to 10; n is an integer; and Evacuum = vacuum energy. For example, in the QVSL transformation, a particle with 10D4d is transformed to a particle with 4D10d from Equation (1f). Calculated from Equation (1e), the rest mass of 4D10d is 1/α12 ≈ 13712 times of the mass of 10D4d. In terms of rest mass, 10D space-time has 4d with the lowest rest mass, and 4D space-time has 10d with the highest rest mass. Rest mass decreases with increasing space-time dimension number. The decrease in rest mass means the increase in vacuum energy (Evacuum, D), so vacuum energy increases with increasing space-time dimension number. The vacuum energy of 4D particle is zero from Equation (1g). The mass dimension number is limited from 4 to 10, because 4D is the minimum space-time, and 11D membrane and 10D string are equal in the speed of light, rest mass, and vacuum energy. Since the speed of light for >4D particle is greater than the speed of light for 4D particle, the observation of >4D superluminal particles by 4D particles violates casualty. Thus, >4D particles are hidden particles with respect to 4D particles. Particles with different space-time dimensions are transparent and oblivious to one another, and separate from one another if possible.
In the digital representation component for the computer simulation process, data in physical reality are re- presented by digital representations. Both data and digital representations exist. For the digital representation component of physical reality, the three intrinsic data (properties) are rest mass-kinetic energy, electric charge, and spin which are represented by the digital space structure, the digital spin, and the digital electric charge, respectively.
2.2. Digital Space Structure
The digital representations of rest mass and kinetic energy are 1 as attachment space for the space of matter and 0 as detachment space for the zero-space of matter, respectively [7] [11] . In the digital space structure, attachment space attaches to matter permanently or reversibly. Detachment space detaches from the object at the speed of light. Attachment space relates to rest mass and reversible movement, while detachment space relates to irreversible kinetic energy.
As shown previously [8] , our universe is the dual asymmetrical positive-energy-negative-energy universe where the positive-energy universe on attachment space absorbed the interuniversal void on detachment space to result in the combination of attachment space and detachment space. The combination of n units of attachment space as 1 and n units of detachment space as 0 brings about three different digital space structures: binary partition space, miscible space, or binary lattice space as below.
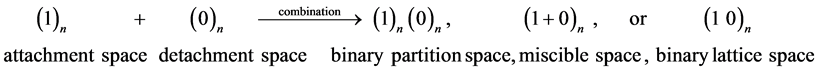 (2)
(2)
Binary partition space, (1)n(0)n, consists of two separated continuous phases of multiple quantized units of attachment space and detachment space. In miscible space, (1 + 0)n, attachment space is miscible to detachment space, and there is no separation of attachment space and detachment space. Binary lattice space, (1 0)n, consists of repetitive units of alternative attachment space and detachment space. Binary partition space, miscible space, and binary lattice space relate to quantum mechanics, special relativity, and force fields, respectively [7] .
Bounias and Krasnoholovets [12] propose that the reduction of dimension can be done by slicing dimension, such as slicing 3 space dimension object (block) into infinite units of 2 space dimension objects (sheets). As shown previously [8] , the positive-energy 10D4d particle universe as our observable universe with high vacuum energy was transformed into the 4D10d universe with zero vacuum energy at once, resulting in the inflation. During the Big Bang following the inflation, the 10d (mass dimension) particle in attachment space denoted as 1 was sliced by detachment space denoted as 0. For example, the slicing of 10d particle into 4d particle is as follows.
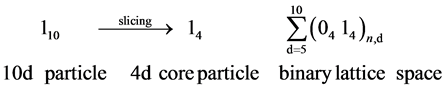 (3)
(3)
where 110 is 10d particle; 14 is 4d particle; d is the mass dimension number of the dimension to be sliced; n as the number of slices for each dimension; and (04 14)n is binary lattice space with repetitive units of alternative 4d attachment space and 4d detachment space. For 4d particle starting from 10d particle, the mass dimension number of the dimension to be sliced is from d = 5 to d = 10. Each mass dimension is sliced into infinite quantized units (n = ∞) of binary lattice space, (04 14)∞. For 4d particle, the 4d core particle is surrounded by 6 types (from d = 5 to d = 10) of infinite quantized units of binary lattice space. Such infinite quantized units of binary lattice space represent the infinite units (n = ∞) of separate virtual orbitals in a gauge force field, while the dimension to be sliced is “mass dimensional orbital” (DO), representing a type of gauge force field. In addition to the six DO’s for gauge force fields from d = 5 to d = 10, gravity appears as the seventh DO at d = 11. As a result, there are seven mass dimensional orbitals as in Figure 1.
2.3. The Digital Spin
The digital representations of the exclusive and the inclusive occupations of positions are 1/2 spin fermion and integer spin boson, respectively [7] . Fermions, such as electrons and protons, follow the Pauli exclusion principle which excludes fermions of the same quantum-mechanical state from being in the same position. Bosons, such as photons or helium atoms, follow the Bose-Einstein statistics which allows bosons of the same quantum-mechanical state being in the same position. As a result, the digital representations of the exclusive and the inclusive occupations of positions are 1/2 spin fermion and integer spin boson, respectively. The symmetry between fermion and boson is supersymmetry. Two supersymmetry transformations from boson to fermion and from fermion to boson yield a spatial translation. In physical reality, supersymmetry is varying supersymmetry [8] . In varying supersymmetry, the repetitive transformation between fermion and boson brings about a spatial translation and the transformation into the adjacent mass dimension number. Varying supersymmetry transformation is one of the two steps in transformation involving the oscillation between 10D particle and 4D particle. The transformation during the oscillation between 10D particle and 4D particle involves the stepwise two-step transformation consisting of the QVSL transformation and the varying supersymmetry transformation. The QVSL
![]()
Figure 1. The seven mass dimensions as mass dimensional orbitals.
transformation involves the transformation of space-time dimension, D whose mass increases with decreasing D for the decrease in vacuum energy. The varying supersymmetry transformation involves the transformation of the mass dimension number, d whose mass decreases with decreasing d for the fractionalization of particle, as follows.
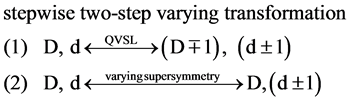 (4)
(4)
The repetitive stepwise two-step transformation between 10D4d and 4D4d as follows.
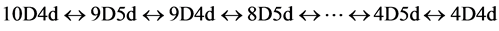 (5)
(5)
In this two-step transformation, the transformation from 10D4d to 9D5d involves the QVSL transformation as in Equation (1d). Calculated from Equation (1e), the mass of 9D5d is 1/α2 ≈ 1372 times of the mass of 10D4d. The transformation of 9D5d to 9D4d involves the varying supersymmetry transformation. In the normal supersymmetry transformation, the repeated application of the fermion-boson supersymmetry transformation carries over a boson (or fermion) from one point to the same boson (or fermion) at another point at the same mass. In the varying supersymmetry transformation, the repeated application of the fermion-boson supersymmetry transformation carries over a boson from one point to the boson at another point at different mass dimension number in the same space-time number. The repeated varying supersymmetry transformation carries over a boson Bd into a fermion Fd and a fermion Fd to a boson Bd−1, which can be expressed as follows
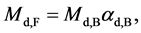 (6a)
(6a)
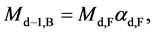 (6b)
(6b)
where Md, B and Md, F are the masses for a boson and a fermion, respectively; d is the mass dimension number; and αd, B or αd, F is the fine structure constant that is the ratio between the masses of a boson and its fermionic partner. Assuming a’s are the same, it can be expressed as
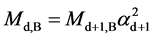 . (6c)
. (6c)
2.4. The Digital Electric Charge
As described before [13] , the digital representations of the allowance and the disallowance of irreversible kinetic energy are integral electric charges and fractional electric charges, respectively. Individual integral charge with irreversible kinetic energy to cause irreversible movement is allowed, while individual fractional charge with irreversible kinetic energy is disallowed. The disallowance of irreversible kinetic energy for individual fractional charge brings about the confinement of individual fractional charges to restrict the irreversible movement resulted from kinetic energy. Collective fractional charges are confined by the short-distance confinement force field where the sum of the collective fractional charges is integer. As a result, fractional charges are confined and collective. The confinement force field includes gluons in QCD (quantum chromodynamics) for collective fractional charge quarks in hadrons and the magnetic flux quanta for collective fractional charge quasiparticles in the fractional quantum Hall effect (FQHE) [14] - [16] .
In the periodic table of elementary particles, fractional charge quarks have their own seven mass dimensional orbitals as the seven auxiliary mass dimensional orbitals in addition to the seven principal mass dimensional orbitals for leptons as in Figure 2.
2.5. The Selective Retention Component
The selective retention component retains selectively events in a narrative. The retained events are unified by the common narrative. The narrative of physical reality is the four-stage evolution of our cyclic dual universe. The four force fields are unified by the four-stage evolution.
Our dual universe is the globally reversible cyclic dual universe as shown in Figure 3 [7] for the evolution of our universe as described previously [7] .
The four reversible stages in the globally reversible cyclic dual universe are: 1) the formation of the 11D
![]()
Figure 2. Leptons and quarks in the seven principal dimensional orbitals (solid lines) denoted by the principal dimensional orbital number d and the seven auxiliary dimensional orbitals (dash-dotted lines) denoted by the auxiliary dimensional number a.
![]()
Figure 3. The globally reversible cyclic dual universe.
membrane dual universe; 2) the formation of the 10D string dual universe; 3) the formation of the 10D particle dual universe; and 4) the formation of the asymmetrical dual universe. The pre-strong force (the prototype of observed strong force) and pre-gravity emerged in the stage 2. The pre-electromagnetism emerged in the stage 3, while the weak force emerged in the stage 4. The selective retention of the four force fields provides the four force fields (gauge bosons) for the four of the seven principal mass dimensional orbitals (Bd) as in Table 1. The other three of the seven principal mass dimensional orbitals are for the CP (right) nonconservation, the CP (left) nonconservation, and the weak (right) force.
The periodic table of elementary particles for leptons, quarks, and gauge boson is in Table 2 with both the principal mass dimensional orbital numbers and the auxiliary mass dimensional orbital numbers.
3. The Gauge Boson Mass Formula and the Cosmic Ray Mass Formula
The gauge boson mass formula is Equation (7) derived from Equation (6c) based on the digital spin structure,
![]() . (7)
. (7)
Each dimension has its own αd, and all αd’s except α7 (αw) of the seventh dimension (weak interaction) are equal to α, the fine structure constant of electromagnetism. The lowest energy boson is the Coulombic field for electromagnetism based on Equation (6b) and the second lowest boson energy is p1/2 (a spin 1 boson as a half of the spin 0 pion) with the mass of 70 MeV for the strong interaction. As described in Section 4, this boson B6 is used to construct gluon.
![]()
Table 1. The masses of the principal mass dimensional orbitals (gauge bosons) α = αe, d = mass dimensional orbital number.
![]()
Table 2. The periodic table of elementary particles d = principal mass dimensional orbital number, a = auxiliary mass dimensional orbital number.
![]() . (8a)
. (8a)
![]() (8b)
(8b)
In Table 1, αw is not same as α because there is a mixing between electromagnetism and the weak interaction in the standard theory of the electroweak interaction, and sinqw is not equal to 1 where qw is the weak mixing angle [17] . As a result, αw instead of a is used to calculate ![]() from
from ![]() based on the gauge boson formula Equation (7).
based on the gauge boson formula Equation (7). ![]() is the mass of weak Z boson MZ which is 91.1876 GeV.
is the mass of weak Z boson MZ which is 91.1876 GeV.
![]() (9)
(9)
The calculated value for αw is 0.02771. As described in the following paragraphs and Table 3, B8, F9 and B9 in Table 2 are observed in cosmic rays as the first knee, the second knee, and the toe, respectively, where the calculated masses are in good agreement with the observed masses [6] . The calculated energy for B11 is 1.13 × 1019 GeV in good agreement with the Planck mass, 1.22 × 1019 GeV for gravity.
High-energy cosmic rays which have much higher energies than the energy of particles accelerated by the Large Hadron Collider provide the study of elementary particles beyond the capacity of particle accelerators. The cosmic ray mass formula is to the energy spectrum for the knees-ankles-toe of cosmic rays [6] . The energy spectrum from 109 eV to 1020 eV appears to follow a single power law except few breaks at the knees-ankles-toe [18] . The power index increases at the first knee and the second knee, and decreases at the ankle. Above 4 × 1019 eV, the power index increases as the “toe”. The fine structure of the cosmic ray spectrum [19] shows that an ankle with decrease in power index is in between the first knee and the second knee, resulting in two knees, two ankles, and one toe. As explained previously [6] , the knees-ankles-toe are explained by the very high-energy fermions and bosons in the periodic table of elementary particles. In the periodic table, some high-energy dimensional fermions (Fd where d = dimen-
![]()
Table 3. The calculated masses for dimensional bosons-fermions and the observed eV for the knees-ankles-toe. Bd = mass dimensional boson, Fd = mass dimensional fermion.
sional orbital number from 5 to 11) and bosons (Bd) are involved in the knees-ankles-toe. At the knees and the toe, some parts of the energies from the energy sources of cosmic rays are spent to generate Fd and Bd, resulting in the increase of power index. The ankles are the the middle points (midpoints) between the adjacent dimensional fermions and bosons. At a midpoint, the energy is too high to keep the thermally unstable high- energy dimensional particle, resulting in the decay and the decrease of power index.
The cosmic ray mass formula is derived from Equations (6a) and (6b)
![]() (10a)
(10a)
![]() (10b)
(10b)
where Md,B and Md,F are the masses for a boson and a fermion, respectively; d is the mass dimension number from 8 to 10; and ad,B or ad,F is the fine structure constant. The midpoint is expressed as follows.
![]() (11)
(11)
The calculated masses of B8, the midpoint, F9, the midpoint, and B9, are 1.7 × 1015, 2 × 1016, 2.4 × 1017, 2.8 × 1018, and 3.2 × 1019 eV, respectively, which are in good agreement with observed 3 × 1015, 2 × 1016, 3 × 1017, 3 × 1018, and 4 × 1019 eV for the first knee, the first ankle, the second knee, the second ankle, and the toe, respectively as in Table 3.
The mass of F10 is 4.4 × 1021 eV beyond the GZK (Greisen-Zatsepin-Kuzmin) limit, which occurs at about 5 × 1019 eV, as the maximum energy of cosmic ray particles that have traveled long distances (about 160 million light years), due to the theoretical energy losses of higher-energy ray particles and to scattering from photons in the cosmic microwave background. Therefore, F10 and above are not observed.
4. The Lepton Mass Formula and the Quark Mass Formula
The lepton mass formula and the quark mass formula are derived from the electric digital charge structure where the digital representations of the allowance and the disallowance of irreversible kinetic energy are integral electric charges and fractional electric charges, respectively [13] . The collectivity of fractional charges requires the attachment of energy as flux quanta to bind fractional charges. As a result, the integer-fraction transformation from integral charges to fractional charges involves the integer-fraction transformation to incorporate flux quanta similar to the composite fermion theory for the FQHE [20] [21] . In the composite fermion model, the formation of composite fermion is through the attachment of an even number of magnetic flux quanta to electron, while the formation of composite boson is through the attachment of an odd number of magnetic flux quanta to electron. In the same way, the integer-fraction transformation from integral charges to fractional charges for quarks consists of the three steps: 1) the attachment of an even number of flux quanta to individual integral charge fermions to form individual integral charge composite fermions (Fc); 2) the attachment of an odd number of flux quanta to individual integral charge composite fermions to form transitional collective integral charge composite bosons (Bc); and 3) the conversion of flux quanta into the confinement force field to confine collective fractional charge composite quarks (Qc) converted from composite bosons as follows.
![]() (12)
(12)
where Fc, Bc, and Qc are the composite fermion the composite boson, and the composite quark, respectively. The first step of the integer-fraction transformation from electron to quark is the attachment of 2 flux quanta to individual integral charge electrons to form individual composite fermions (Fc’s). The flux quanta (70.0252 MeV) are the flux quanta as proposed by Peter Cameron to calculate accurately the masses of pion, muon, and proton [22] . The quantum of 70.0252 MeV is also the bosonic mass quantum proposed by Malcolm H. MacGregor for a basic building block to calculate accurately the masses of hadrons [23] . According the periodic table of elementary particles, the flux quantum is B6 from Table 1. From Equation (6b), the relationship between B6 and electron (F5) is as follows.
![]() (13)
(13)
where α is the fine structure constant for electromagnetism. The Fpc (the principal composite fermion) consists of two B6 as flux quanta.
![]() (14)
(14)
The mass of pion (boson) is the mass of the principal composite fermion (Fpc) minus the mass of electron (fermion) [22] .
![]() (15)
(15)
which is in excellent agreement with the observed 139.5702 MeV.
In the second step for the attachment of odd number of flux quanta, the odd number of flux quanta can be one flux quantum for one principal composite fermion or three flux quanta for three principal composite fermions, resulting in lepton or quark, respectively. For the formation of lepton, the second step is the attachment of one flux quantum to one individual integral charge principal composite fermion to form the transitional integral charge principal composite boson. In the second step, the principal composite boson for composite lepton is B6 + Fpc. In the third step, the principal composite boson is converted into two composite leptons (Lc) with the addition of electrons, resulting in muon as follows.
![]() (16a)
(16a)
![]() (16b)
(16b)
which is in excellent agreement with the observed 105.6584 MeV. The muon mass formula in Equation (16b) is identical to the Barut lepton mass formula for muon [24] . Equation (16b) explains the origin of 3/2 which cannot be explained easily by Cameron, MacGregor, and Barut. Without binding the composite leptons together by the flux quanta, leptons have integral electric charges instead of fractional electric charges.
The Barut lepton mass formula [24] is expressed as follows.
![]() , (17)
, (17)
where n = 0, 1, and 2 are for e, m, and t, respectively. The calculated mass of t is 1786.2 MeV in good agreement with
the observed mass as 1776.82 MeV. According to Barut, the second term, ![]() of the mass formula is for the Bohr-
of the mass formula is for the Bohr-
Sommerfeld quantization for a charge-dipole interaction in a circular orbit. The experimental proof of this dipole-interaction in a circular orbit is shown as the light boson at 17 MeV from the generation of pairs of electrons and positrons by firing protons at thin targets of lithium-7 [25] [26] . The light boson is the orbit ![]() in the circular orbit. The masses of the bosons from orbit
in the circular orbit. The masses of the bosons from orbit ![]() are calculated as follows.
are calculated as follows.
![]() (18)
(18)
where the masses of the bosons for n = 1 and 2 are 2Me for ![]() (electron-positron pair) and 34Me for the light boson, respectively. The calculated mass of the light boson is 17.374 MeV in excellent agreement with the observed mass as 17 MeV [25] . As in Figure 2 and Table 2, nm and nt share the same orbitals with m and t, respectively. All neutrinos (ne, nm and nt) in the periodic table of elementary particles (Table 2) are nearly massless because of chiral symmetry (permanent left-handed).
(electron-positron pair) and 34Me for the light boson, respectively. The calculated mass of the light boson is 17.374 MeV in excellent agreement with the observed mass as 17 MeV [25] . As in Figure 2 and Table 2, nm and nt share the same orbitals with m and t, respectively. All neutrinos (ne, nm and nt) in the periodic table of elementary particles (Table 2) are nearly massless because of chiral symmetry (permanent left-handed).
For the formation of quark, the second step is the attachment of 3 flux quanta (B6’s) to three individual integral charge principal composite fermions (Fpc’s) to form the transitional collective integral charge principal composite bosons (Bpc’s). The transitional principal composite bosons are derived from the combination of the three principal composite fermions (3 Fpc’s) with the three flux quanta (3 B6’s) which are connected and located at the same position in the same 3-Fpc energy level. One 3-Fpc energy level consists of the three connected Fpc sites with the connected three flux quanta (3 B6’s). The mass of the transitional principal composite bosons Bpc is as follows.
![]() (19)
(19)
In the third step, 3 flux quanta (B6’s) are converted to 3-color gluons (red, green, and blue) in QCD. Each of the three Fpc sites in the energy level has ±1/3 charge. The fractional charges of quarks are the integer multiples of ±1/3e. One principal composite boson (Bpc) is converted into two composite quarks (fermions) in the same way as the conversion of one photon (boson) into two fermions (electron-positron). As a result, the principal composite quark (Qpc) has 1/2 mass of the principal composite boson (Bpc) in addition to the mass of 1/3 and 2/3 electrons for the three Fc sites for different electric charges as follows.
![]() (20)
(20)
From Equation (20), the principal composite quark with 1/3 electric charge is the principal composite d quark with 315.28 MeV, and the principal composite quark with 2/3 charge is the principal composite u quark with 315.45 MeV.
According to the periodic table of elementary particles (Table 2), quarks have the auxiliary mass dimensional orbital in addition to the principal mass dimensional orbital as in Figure 2. As a result, there are the auxiliary composite quarks (Qac) in addition to the principal composite quarks (Qpc). The three-step transformation in the integer-fraction transformations from integral charge to fractional charge is applicable to the auxiliary composite quarks. The auxiliary flux quantum is Ba7 which is in between d7 and d8 as shown in Figure 2. As a result, αw instead of α is used for Ba7. Muon, a composite lepton, instead of electron is used for Ba7 as follows.
![]() (21)
(21)
where αw is the fine structure constant for weak force from Equation (9). In the first step, the Fac (the auxiliary composite fermion) consists of two Ba7 as auxiliary flux quanta.
![]() (22)
(22)
The second step is the attachment of 3 auxiliary flux quanta (Ba7’s) to the individual integral charge auxiliary composite fermions (Fac’s) to form the transitional collective integral charge auxiliary composite bosons (Bac’s). The transitional auxiliary composite bosons are derived from the combination of the three auxiliary composite fermions (3 Fac’s) with the three flux quanta (3 Ba7’s) which are connected and located at the same position in the same 3-Fac energy level. One 3-Fac energy level consists of the three connected Fac sites with the connected three auxiliary flux quanta (3 Ba7’s). The mass of the transitional auxiliary composite bosons Bac is as follows.
![]() (23)
(23)
In the third step, 3 auxiliary flux quanta (Ba’s) are converted to 3-color gluons (red, green, and blue) in QCD to confine the collective fractional charge auxiliary composite quarks (Qac’s) conversed from the transitional auxiliary composite bosons (Bac’s). One composite boson (Bac) is converted into two composite quarks (fermions) in the same way as the conversion of one photon (boson) into two fermions (electron-positron). As a result, the auxiliary composite quark (Qac) has 1/2 mass of the auxiliary composite boson (Bac).
![]() (24)
(24)
The composite quark mass formula is the combination of the principal composite quark and the auxiliary composite quark with the Bohr-Sommerfeld quantization for a charge-dipole interaction in a circular orbit as follows.
![]() (25)
(25)
where n = 1, 2, 3, 4, and 5 for u/d, s, c, b, and a part of t, respectively.
At n = 5 for Equation (25), the mass (140.4 GeV) is greater than B7 (91.1876 GeV) as in Table 1, so the last two auxiliary mass dimensional orbitals of the seven auxiliary dimensional orbitals are in between d8 and d9. The formation of the auxiliary mass dimensional orbitals between d8 and d9 requires the extra-principal flux quantum as B7 instead of B6. For the first step in the three-step transformation from integer charge to fractional charge for the extra quarks is to form the extra composite fermion. B7 is Z boson. The Fepc (the extra principal composite fermion) consists of two B7 as flux quanta. The Fepc (the extra principal composite fermion) consists of two B7 as flux quanta.
![]() (26)
(26)
For the second step to form the extra principal composite boson, only one extra-principal flux quantum is added to one extra-principal composite fermion, because the 3-color principal electric and 3-color auxiliary flux quanta already exist, and there is no need for three extra-principal flux quanta.
![]() (27)
(27)
The third step is the conversion of the extra-principal composite boson to two extra-principal quarks (Qepc). Only The neutral Bepc is used for Qepc, so no electron is added.
![]() (28)
(28)
Since Qepc involves only one extra-principal flux quantum, Qepc is identical to the extra-composite lepton Lec which is neutral extra-muon![]() .
.
![]() (29)
(29)
The extra-auxiliary flux quantum is Bea is like Equation (21).
![]() (30)
(30)
where the fine structure constant in between d8 and d9 is α. For the first step in the three-step transformation from integer charge to fractional charge, the extra-auxiliary composite fermion (Feac) is the composite of two B8ea’s.
![]() (31)
(31)
For the second step to form the extra-auxiliary composite boson Beac, only one extra-auxiliary flux quantum is needed in the same way for the formation of the extra-principal composite boson.
![]() (32)
(32)
For the third step to form quark from composite boson Beac, extra-auxiliary composite boson is converted into two extra-auxiliary composite quarks (Qeac).
![]() (33)
(33)
The mass formula for the extra- composite quark (Qec) with the Bohr-Sommerfeld quantization for a charge-di- pole interaction in a circular orbit is as follows.
![]() (34)
(34)
where n' = 1 and 2 for b and t, respectively.
Quark is the combination of the composite quark from Equation (25) and the extra-composite quark from Equation (34). The quark mass formula is as follows.
![]() (35)
(35)
where n =1, 2, 3, 4, and 5 for d/u. s, c, b, and t, respectively; and n' = 1 and 2 for b and t respectively. The calculated masses for d, u, s, c, b, and t are 328.4 MeV, 328.6 MeV, 539 MeV, 1605.3 MeV, 4974.6 MeV, and 175.4 GeV, respectively. In the Standard Model, there are three generations of leptons. Extra-muon ![]() is outside of the three generations of leptons in the Standard Model, so
is outside of the three generations of leptons in the Standard Model, so ![]() is hidden as shown in Table 2. As shown in Table 2, to be symmetrical to the hidden
is hidden as shown in Table 2. As shown in Table 2, to be symmetrical to the hidden![]() , the extra composite quark, (Qepc) and the extra auxiliary composite quark (Qeac) for b quark are also hidden (absent).
, the extra composite quark, (Qepc) and the extra auxiliary composite quark (Qeac) for b quark are also hidden (absent).
The calculated mass of top quark is 175.4 GeV in good agreement with the observed 173.3 GeV. The calculated masses are the constituent masses which include all different types of the flux quanta (B6, B7a, B8, and B8ea). The calculated constituent masses are comparable to the quark masses proposed by De Rujula, Georgi, and Glashow [27] , Griffiths [28] , and El Naschie [29] . The masses of hadrons are the combinations of the constituent quark masses minus the binding energy in the hadronic bond among quarks [30] [31] . The hadronic bond is the overlapping of the auxiliary dimensional orbitals, so it involves the auxiliary composite quarks, consisting of the primary auxiliary composite quark (Qac) from Equation (24), the secondary auxiliary composite quark (![]() ), and the tertiary auxiliary composite quark (
), and the tertiary auxiliary composite quark (![]() ). The secondary auxiliary composite quark (
). The secondary auxiliary composite quark (![]() ) is generated from the primary auxiliary composite quark in the same way as Equation (24).
) is generated from the primary auxiliary composite quark in the same way as Equation (24).
![]() (36)
(36)
The tertiary auxiliary composite quark (![]() ) is generated from the secondary auxiliary composite quark in the same way as Equation (36).
) is generated from the secondary auxiliary composite quark in the same way as Equation (36).
![]() (37)
(37)
For neutron, the binding energy (EQ-Q) in the hadronic bond between quarks involves the primary auxiliary composite quark to become the binding energy and the secondary auxiliary composite quark to become the mass to replace the primary auxiliary composite quark as below.
![]() (38)
(38)
The mass of neutron which has two hadronic bonds is the sum of the constituent masses of u, d, and d quarks minus the binding energy from the two hadronic bonds.
![]() (39)
(39)
The calculated mass of neutron is in good agreement with the observed value 939.57 MeV.
Proton is more stable than neutron, so it involves the additional binding energy from the tertiary auxiliary composite quark as below.
![]() (40)
(40)
The mass of proton which has two hadronic bonds is the sum of the constituent masses of u, u, and d quarks minus the binding energy from the two hadronic bonds.
![]() (41)
(41)
The calculated mass of proton is in good agreement with the observed value 938.21 MeV.
Another way to form hadrons is through the combinations of Me/α (= 70.03 MeV) and 3Me/2α (= 105.04 MeV) as the mass quanta (mass building blocks) by the MacGregor’s constituent quark model [23] [32] . Therefore, the masses of hadrons can be calculated by the combinations of the constituent quark masses from the quark mass formula as Equation (35) and by the combinations of the mass quanta from the MacGregor’s constituent quark model [23] [30] - [32] . Another type of quark mass is the current mass which is much lower than the constituent mass, because it does not include some parts of principal composite quark (Qpc) and auxiliary composite quark (Qac) which become massless gluon [28] [33] .
Another extra-muon is charge extra-muon, ![]() , derived from W± boson. The formation of
, derived from W± boson. The formation of ![]() is same as
is same as ![]() based on Equations (28) and (29). (The observed mass of W boson is 80.385 GeV.)
based on Equations (28) and (29). (The observed mass of W boson is 80.385 GeV.)
![]() (42)
(42)
Extra-muon ![]() includes neutral
includes neutral ![]() and charge
and charge![]() .
.
5. The Higgs Boson Mass Formula
In the conventional model, under spontaneous symmetry breaking, zero-energy ground state space turns into the nonzero-energy scalar Higgs Field which exists permanently in the universe. The problem with such nonzero-energy field is the cosmological constant problem from the huge gravitational effect by the nonzero-energy Higgs field [34] . The coupling of massless particle to the Higgs field produces the transitional nonzero-energy Higgs field-particle composite which under spontaneous symmetry restoring produces the massive particle with the longitudinal component on zero-energy ground state space without the Higgs field as follows.
![]() (43)
(43)
To avoid the cosmological problem from the huge gravitational effect by the nonzero-energy Higgs field is to make the Higgs field a transitional field which exists momentarily and to make zero-energy ground state space a permanent zero-energy ground state space which exists permanently in the universe [8] . For the digital space structure, such zero-energy ground state space is zero-energy attachment space which attaches particles to account for the longitudinal component, mass, and reversible movement. Unlike the conventional model, attachment space actively couples to massless particle. Under spontaneous symmetry breaking, the coupling of massless particle to zero-energy attachment space produces the transitional nonzero-energy Higgs field-particle composite which under spontaneous symmetry restoring produces massive particle on zero-energy attachment space with the longitudinal component without the Higgs field as follows.
![]() (44)
(44)
The opposite of attachment space is zero-energy detachment space which detaches particles to account for irreversible kinetic energy. Unlike the conventional model, detachment space actively couples to massive particle. Under spontaneous symmetry breaking, the coupling of massive particle to zero-energy detachment space produces the transitional nonzero-energy reverse Higgs field-particle composite which under spontaneous symmetry restoring produces massless particle on zero-energy detachment space without the longitudinal component without the reverse Higgs field as follows.
![]() (45)
(45)
For the electroweak interaction in the Standard model where the electromagnetic interaction and the weak interaction are combined into one symmetry group, under spontaneous symmetry breaking, the coupling of the massless weak W, weak Z, and electromagnetic A (photon) bosons to zero-energy attachment space produces the transitional nonzero-energy Higgs fields-bosons composites which under partial spontaneous symmetry restoring produce massive W and Z bosons on zero-energy attachment space with the longitudinal component without the Higgs field, massless A (photon), and massive Higgs boson as follows.
![]() (46)
(46)
Being outside of the three-generation lepton-quark in the Standard Model, the Higgs boson adopts the extra- muon condensate ![]() which is outside of the three-generation lepton-quark. In other words, the extra-muon condensate becomes the Avatar Higgs boson [5] . The extra-muon condensate
which is outside of the three-generation lepton-quark. In other words, the extra-muon condensate becomes the Avatar Higgs boson [5] . The extra-muon condensate ![]() includes
includes ![]() and
and![]() .The extra-muon condensate composite consists of
.The extra-muon condensate composite consists of![]() ,
, ![]() , and
, and![]() . From Equations (29) and (42), the mass of the
. From Equations (29) and (42), the mass of the ![]() condensate composite as the Higgs boson composite is as follows.
condensate composite as the Higgs boson composite is as follows.
![]() (47)
(47)
This extra-muon condensate composite as the Higgs boson composite at 750 GeV is in good agreement with the 756 GeV diphoton excess observed from the Large Hadron Collider (LHC) with zero charge and zero spin [35] [36] . The ![]() condensate composite decays into three
condensate composite decays into three ![]() condensates. Just as the observed top quark is a bare quark with the observed mass of about 173 GeV instead of about 346 GeV (two times 173 GeV) for top quark-antitop quark boson, the observed mass of
condensates. Just as the observed top quark is a bare quark with the observed mass of about 173 GeV instead of about 346 GeV (two times 173 GeV) for top quark-antitop quark boson, the observed mass of ![]() as the Higgs boson is the mass of bare m' as follows.
as the Higgs boson is the mass of bare m' as follows.
![]() (48)
(48)
The calculated mass (126 GeV) is in excellent agreement with the observed 125 GeV [37] or 126 GeV [38] .
6. Conclusions
One of the biggest unsolved problems in physics is the particle masses of all elementary particles which cannot be calculated accurately and predicted theoretically. In this paper, the unsolved problem of the particle masses is solved by the accurate mass formulas which calculate accurately and predict theoretically the particle masses of all leptons, quarks, gauge bosons, the Higgs boson, and cosmic rays (the knees-ankles-toe) by using only five known constants: the number (seven) of the extra spatial dimensions in the eleven-dimensional membrane, the mass of electron, the masses of Z and W bosons, and the fine structure constant. The calculated masses are in excellent agreements with the observed masses. For examples, the calculated masses of muon, top quark, pion, neutron, and the Higgs boson are 105.55 MeV, 175.4 GeV, 139.54 MeV, 939.43 MeV, and 126 GeV, respectively, in excellent agreements with the observed 105.65 MeV, 173.3 GeV, 139.57 MeV, 939.27 MeV, and 126 GeV, respectively. The mass formulas also calculate accurately the masses of the new particle at 750 GeV from the LHC and the new light boson at 17 MeV. The theoretical base of the accurate mass formulas is the periodic table of elementary particles. As the periodic table of elements is derived from atomic orbitals, the periodic table of elementary particles is derived from the seven principal mass dimensional orbitals and seven auxiliary mass dimensional orbitals. All elementary particles including leptons, quarks, gauge bosons, the Higgs boson, and cosmic rays can be placed in the periodic table of elementary particles.
The periodic table of elementary particles is derived from the theory of everything as the computer simulation model of physical reality consisting of the mathematical computation, digital representation and selective retention components. The mathematical computation involves oscillating M-theory as oscillating membrane-string- particle whose space-time dimension (D) oscillates between 11D and 10D and between 10D and 4D. For the digital representation component, the three intrinsic data (properties) are rest mass-kinetic energy, electric charge, and spin which are represented by the digital space structure, the digital spin, and the digital electric charge, respectively. The digital representations of rest mass and kinetic energy are 1 as attachment space for the space of matter and 0 as detachment space for the zero-space of matter. The digital representations of the exclusive and the inclusive occupations of positions are 1/2 spin fermion and integer spin boson, respectively. The digital representations of the allowance and the disallowance of irreversible kinetic energy are integral electric charges and fractional electric charges, respectively. For the selective retention component, gravity, the strong
![]()
Table 4. The mass formulas of gauge bosons, cosmic rays, leptons, quarks, and the Higgs boson.
force, electromagnetism, and the weak force are the retained events during the reversible four-stage evolution of our universe, and are unified by the common narrative of the evolution. The computer simulation model of physical reality provides the seven principal mass dimensional orbitals and seven auxiliary mass dimensional orbitals to place leptons, quarks, gauge bosons, the Higgs boson, and cosmic rays in the periodic table of elementary particles.
The summary of the mass formulas is in Table 4.