Complex Systems Are Not Black Boxes but Solvable Systematical Problems; Proven by Simulation and New Conception ()
Received 9 July 2016; accepted 27 August 2016; published 30 August 2016

1. Introduction
This paper presents an incredible scientific solution for complex systems based on multidisciplinary physics and engineering to scientists engaged in those fields. Complex systems represent unsolvable problems in science, such as black holes, sun magnetism, nuclear fusion, nuclear theory, super conductor, plasma, turbulence, climate change, and the subconscious in human. Many scientists have said that these phenomena are mysterious science that can be solved by God alone and not by humans. Many geniuses in the field of physics have attempted to find answers to these questions over the last century, but nobody has succeeded yet.
In addition, famous research organizations, such as the Santa Fe Institute (SFI) in the United States, have worked to study the complexity originating from complex systems. The SFI was established by Dr. Murray Gell-Mann (1929) and other scientists based on their mission of statement (http://www.santafe.edu/about/mission-and-vision/). However, they have not yet succeeded in spite of the money, time, and effort expended by many scientists. This leaves us to wonder: Does science have a solution to these problems?
The answer is here. If someone discovered a solution for the algorithm of complex systems in other sciences, the other approximately ten million physicists in the world might say that it is an unbelievable miracle in science, or a trick. However, the author would like to present a report on complex systems to these scientists for careful reading. The report was previously published in this journal in October 2015 [1] ; it contains an incredible scientific result, which is as follows. Natural systems, such as the stock market system, ecological systems, or thermodynamic systems, are not black boxes; rather they are solvable systematic problems such as a closed-loop system with a negative feedback property based on energy conservation (https://en.wikipedia.org/wiki/Conservation_of_energy), as shown in Figure 1. This is the basic concept in the solution.
This can analyzed by the feedback systems analysis method (https://en.wikipedia.org/wiki/Control_theory) based on the automatic control theory [2] in engineering. Nevertheless, this is a serious problem for physicists. Most physicists do not use the analysis method in conventional physics, based on reductionism. Accordingly, most physicists cannot read the report written by the method and they cannot accept the research result. Why do not they use the method? There is a hidden serious and important thing in physical science. It is involved with the principal rule of physics (https://en.wikipedia.org/wiki/Physics), according to which, most physical phenomena in nature must be “quantitative and qualitative”, and “measureable and reversible”; physicists deal it with the physical science. (It is a keyword in this paper.) The other hand, the external behavior of complex systems such as the stock market or ecosystems is not measureable and reversible within quantitative and qualitative. Instead, it must be solved by a time series function in real time, similar to the systems analysis method in engineering. Refer to Section 3 for more details. Despite of, no argument to physicists; because most physicists have good mathematical capabilities, they begin to study the principle immediately. This is a good idea for physicists and can be vital for the cooperation between physicists and engineers.
In addition, the author proudly provides a system simulator (shown in Figure 2), designed using an electrotype for scientists to proving the research. It is a novel design, which can simulate the behavior of dynamic systems for any type of system in nature; moreover, it can be demonstrated by anyone, at any time, and anywhere. If anyone has a doubt about this research, the author will support a simulator to him/her freely. Finally, complexity is not a mysterious science; this research provides a revolutionary scientific result in modern science. Therefore, if the solution is sufficient, it represents an incredible scientific success and a great discovery, similar to the Copernican theory. Maybe a human is the winner.
Nevertheless, there is another serious issue to consider. Most scientists will not welcome the new solution presented in this report. The following are the possible reasons for this response. Many scientists have a fixed idea, and so it is possible that they absolutely believe that complexity is an unsolvable problem, and they cannot visualize anything that contradicts this belief and is beyond their assertions. Indeed, the report may be shocking and unbelievable for them. Therefore, they may fall into a dilemma, because they cannot contradict against the experimental results. Apart from these concerns, the author would like to stress that the solution is not dangerous
![]()
Figure 1. Mechanism of a complex system.
![]()
Figure 2. Electrotype complex systems simulator (50% size) and the system simulator prototype (available eBay).
to anyone, and that no damage can occur to anybody in case of failure.
2. Experiment and Result
2.1. Experiment
However, the author would like to explain the experiment again using the complex system simulator developed for this, because, many scientists do not believe this research yet. The author has additionally prepared a video to supplement this report (https://youtu.be/-EnU4L5uH5o), the experiment was performed in a sequence of two steps, as shown below.
In step one, the characteristics of all systems can be tested by their response to a unit step function u(t). We add a constant value as a unit step function u(t) to the simulator using a function generator (https://en.wikipedia.org/wiki/Function_generator), and we can then observe the output y(t) as displayed on an oscilloscope (https://en.wikipedia.org/wiki/Oscilloscope) as shown in Figure 3, where the blue line represents the input U(s) and the yellow curve represents the output Y(s). In addition, the original function y(t) is given by Equation (1)
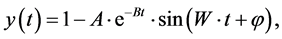 (1)
(1)
where A, B, W, φ are constant, and t is time.
We can find that the output y(t) increases gradually by the input u(t) with a sine wave. This is a well-known characteristic of feedback systems, such as the mechanism as shown in Figure 1, and is similar to a transient phenomenon in electronics. (Further details are provided in [2] .) Nevertheless, we can observe the characteristics of complexity though the yellow curve shown in Figure 3, which is described by Equation (1). For example, the curve displays an initial phenomenon in Figure 3 that is similar to the butterfly effect, whereas the periodic decreasing curve in Figure 3 is similar to the self-organization or fractal. Moreover, the output and input in Figure 3 are not reversible because they have chaotic properties. This is a basic property in complex systems, as shown in Equation (1). For further details about complexity, refer to [4] and other reference books.
In step two, we consider many other cases, where the source of a complex system, such as stock market systems or thermodynamic systems, is not constantly static but is variably dynamic. We add an irregular value as a random function r(t) into U(S). The response to the random function r(t) can be observed in Figure 4; the yellow curve in the figure displays a time-varying output y(t), and we cannot determine anything. Nevertheless, we can make the following observations throughout this simulation, as shown in Figure 3: The four kinds of behavior as mentioned previously overlap as chaotic, fractal, self-organization, butterfly-effect
(https://en.wikipedia.org/wiki/Complex_systems), and other phenomena. Similar to the dynamic daily stock price, dynamic daily climate, or dynamic individuals in ecosystems; in addition, we have found important properties: The input and output are not measurable and reversible, or quantitative and qualitative; and if the input source of a complex system disappears, the output product converges to zero with time. Incidentally, we wonder why
![]()
Figure 3. Response of a unit step function. The lower blue curve shows the unit step function, whereas the upper yellow curve shows the output of the complex system.
![]()
Figure 4. Response of a random function. The blue curve shows the random function, and the yellow curve shows the output of the complex system.
Equation (1) is not reversible between input and output, and further, stock prices cannot be forecast easily and completely.
2.2. Results
We can confirm many characteristics of complex systems through the experiment described above. For instance, complex systems never overflow, never run away to destruction, and are certainly not dangerous, but safe, because once the entropy of the input disappears, the output converges to zero based on the law of conservation of energy. Moreover, complex systems can be externally controlled by humans, but not completely as daily stock prices in the market. Therefore, complex systems are solvable systematic problems and are not black boxes. In people cannot forecast stock prices; if we could, we would be rich. Why cannot we forecast the prices? Because addition, the most important aspects of this study are the dynamic characteristics of the input source and the output products of complex systems. These properties are non-quantitative, non-qualitative, non-measureable, and non-reversible, as illustrated by the many verified complex systems in nature, including economic systems, thermodynamic systems, or ecosystems.
3. Discussion
3.1. Conception
This paper contains a revolutionary solution for complexity in the science of the complex. This solution is not dangerous and no damage to anyone. Moreover, it is easily applicable to science. Therefore, the author would like to share with scientists (including those of the SFI) the origin of the concept. The concept of the solution was discovered in 2008 when the author was cultivating an interest in another science, namely economics, and was surveying complexity in physics. Previously, the author had already studied a course in electrical power and control engineering.
One day, the author discovered strange properties from the stock market while analyzing the pricing of stocks. One of these properties was that the relationship between the transaction volume of a stock and the variations in the stock price are multiplied. Another property is that the equation describing the relationship between a seller
and a buyer,  , [where P(t); stock price in real time, D; time delay, t; time], is
, [where P(t); stock price in real time, D; time delay, t; time], is
based on the law of conservation of energy. Therefore, the relationship between a seller and a buyer in the market is an inverse relationship, and they always counterbalance each other with negative feedback that is related to the “law of supply and demand” in economics. Indirectly, this provided the insight that that the stock market is a feedback system and not a black box, as shown in Figure 1. For more details, refer to [1] .
Furthermore, the author observed a similar phenomenon in other sciences as well. For example, non-linear dynamic systems in a variety of fields exhibit this phenomenon, including representative social economics, nuclear reactor systems in engineering, thermodynamic systems, and ecological systems in nature. Thus, the author discovered that it is possible to solve complex systems using the systems analysis method. Therefore, the author started reporting this discovery to many physical journals. Unfortunately, the author is aware that most scientists in conventional physics do not use or understand systems analysis theory. Consequently, the author decided to design a system simulator that could be used to demonstrate the concept, as shown in Figure 2, based on the basic model system shown in Figure 1. The system simulator can be manufactured at a cost under U.S. $100; further details on this topic are omitted for now.
3.2. Simulator Designing
(Simulator) The design concept for the system simulator is as follows. The basic system feedback model and an equivalent electronic circuit are shown in Figure 5, and are published here for use by scientists. It cleverly comprises an operational amplifier that acts as a comparator, integrator, and differentiator.
The corresponding system transfer function F(s) is
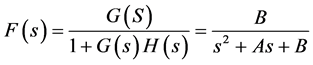 . (2)
. (2)
Next, the electronic circuit transfer function F(s) is
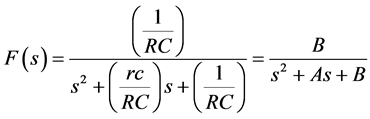 . (3)
. (3)
In Equation (3), the elements [R] and [r] are adjustable via the embedded controller in the simulator. This implies that anyone can experimentally test any system at any time.
![]()
Figure 5. Basic feedback system and the equivalent electronic circuit [3] .
4. Conclusion
Complex systems in nature are not black boxes; rather they are solvable systematic problems. If anyone has a doubt about this research, the author is willing to provide a simulator for him/her. If this paper is acceptable, it provides a revolutionary scientific solution for science, similar to relativity. Furthermore, the scientists (or SFI) can review this report with honor. The author concludes that no more research for complexity and chaos will be disappeared in future.