Received 11 July 2016; accepted 19 August 2016; published 22 August 2016

1. Introduction
Extraction of the state from a dynamic and non-ideal prepared system is of fundamental importance for the quantum computational physics. Contrary to the classical physics, the determination of the quantum state , its diagnostics, requires a large number of N independent measurements [1] [2] . The state of a quantum system in fact is determined by statistical quantities so the probability of the results for any upcoming measurement can be encoded. The entanglement is one of the central mysteries of the quantum mechanics-two or more parties may be committed in some way that is much stronger than the classical way.
, its diagnostics, requires a large number of N independent measurements [1] [2] . The state of a quantum system in fact is determined by statistical quantities so the probability of the results for any upcoming measurement can be encoded. The entanglement is one of the central mysteries of the quantum mechanics-two or more parties may be committed in some way that is much stronger than the classical way.
In this article, we offer a method for measurement of the parameters of a partially unknown or partially coherent superposition of system quantum states. Such a circuit is created, when connecting the magnetic sublevels m = −1, m = 0, and m = 1 of J = 1 level with J = 0 level with laser pulses with linear (π), right circular (σ+), and left circular (σ−) polarizations. There are two ways to select the signal-through optical pumping of the population density of the upper state or through fast pulse excitation. The population density ρee (t) depends from the unknown elements of the superposition, as well as from the laser parameters (intensities and phases). By measuring the signal at different laser parameters, we receive a system of algebraic equations for the unknown elements of the superposition, the latter of which we define. The unknown factor F can be eliminated, taking relations of signals, because it does not depend from the laser parameters. The method of optical pumping has priority over the fast pulse excitation, because it is not compulsory at each new measurement of the signal, the Raby frequencies and the frequency differences to be one and the same.
Upon different laser phases and ellipticities are necessary 16% - 20% more independent measurements of the signal for the determination of the elements of the matrix density, compared to the cases when the unknown state is clear.
By default, the measurement process is assumed to be instantaneous and without defects from the decoherence. In specific experimental situations it is not difficult to be taken into account certain measuring imperfections. As a whole, the obtaining of a probability function in the presence of imperfections and decoherence during the measurement has not been examined sufficiently in depth. This is one of the goals of this document-to determine how the deficiencies and decoherence for quantum filtering affect the measurement
More specifically, the bipartite quantum state рАВ of the systems А and В, is separable, if it can be written as a combination of states of the products рАВ = ∑iрiriA⊗riB as pi ³ 0 and ∑iрi = 1, for certain states riA of the system A and riB of the system В; otherwise рАВ is entangled [3] . But not every entangled state рАВ violates the Bell’s inequalities-some entangled states do not allow hidden variable descriptions [3] .
In practice, an entanglement can be detected by measurement of the “entanglement witnesses”, physical observables with known values, which prove the existence of quantum entanglement in a given state рАВ [4] . But none one of these entanglement witnesses can prove with certainty whether an arbitrary state is entangled or not. On the other hand, the “measurement” of the entanglement plays a similar universal role. According to the generally accepted axioms, the quantum state рАВ is entangled only if there is a non-zero value of any entanglement measurement [5] . Unfortunately, the entanglement measurement is not physically observable.
These widely known limitations on the Bell’s inequalities, the entanglement witnesses and the entanglement measurement raise a fundamental question: How do we universally detect the entanglement by physical observables? The traditional method for solving this problem is to fully characterize the quantum state by diagnostic of the state [6] - [8] , a method that provides full information about the state including, of course, the measurements of the entanglement of the state. But the application of diagnostics of the quantum state requires multiple measurements, а very courageous task for the growing sizes of the system.
A natural solution is to find a way to obtain the value of the entanglement measurement without full diagnostics of the state (FDS). In fact, many efforts were made in this aspect in the last decade [9] - [12] . But the usual techniques to achieve this goal rely mainly on collective measurements of many identical copies of the state рАВ. There is a need of joint measurement of more than one copy of the state (r⊗r for some integer r > 1). This is a bad news for the experimentalists, since the collective measurements are difficult for application rather than the measurement of single-copy observables. Therefore, it is very desirable to be found a method, which detects the entanglement without full diagnostics of the state by measuring only the single-copy observables. The searching of such a method is very active in the recent years with both theoretical simulations and the realization of experiments, leading to positive results in the implementation of such an attractive task [13] [14] .
In this article, we study the possibility for detecting entanglement without full diagnostics of the state by measuring only the single-copy observables. Surprisingly, despite the previous signs, we find that this attractive task, unfortunately is impossible, if only single-copy observables are measured. This means that there is no way to determine with certainty each entanglement measurement or to determine even whether the value is zero or not, without full diagnostics of the state. For greater accuracy, this means that for any set of informationally-in- complete measurements, there are always two different states, an entangled рАВ, and a separable sAB, which give the same results of the study under this measurement. This sounds a bit counter-intuitive at first glance, but as the entanglement is only a single value, while the diagnostics of the quantum state requires measurement of a set of observables, which are informationally-incomplete, there is a need to determine the scale through square of the Hilbert space of the system.
Our observation is that the universal detection of any characteristic without full diagnostics of the state imposes strong geometrical structural conditions for the set of states that have that characteristic. The set of separable states does not fulfill these conditions due to their non-linear nature, and hence the universal detection of entanglement without full diagnostics of the state through the use of single-copy measurements is impossible. There is a good geometric picture of this fact: unless the form of these separable states is not “cylindrical”, it is not possible to find a projection of the space of the state on a lower measurable hyperplane with non-overlap- ping image for the set of separable states or entangled states.
If adaptive measurements are allowed (the observable that must be measured may depend on previous results of measurement), a protocol is applied in [13] , with which it is claimed that was discovered an entanglement of two-qubit state рАВ, through measurements of one copy without full diagnostics of the state. The protocol includes local filters, which require repeated diagnostics on each single qubit, which leads to a bound of the concurrence [15] on the entanglement measurement of рАВ, in case that the single-qubit matrices with reduced density рА and рВ, are not maximally combined.
We design an experiment with which to apply this adaptive protocol as proposed in [13] , and to show that for some рАВ, with the collected experimental data, the state рАВ, is already fully defined. In other words, after the concurrence of рАВ, is defined, the protocol is already leading to full diagnostics of the state of рАВ, i.e. the protocol does not lead to universal entanglement detection without FDS. This complements our constant result with non-adaptive measurements.
In addition, it is worthwhile to underline that to the best of our knowledge that this is the first experimental realization of the quantum filters (or equivalently of the channel for reducing the amplitude) through an auxiliary method. In comparison with the optical platform that does not require additional ancilla qubits for realization of the channel for reduction of the amplitude [13] [16] [17] , our method is more common and may include other systems directly.
We demonstrate also that if joint measurements of r-copies (i.e. rАБ⊗r ) are allowed even for r = 2 can be found protocols that detect the entanglement of рАВ, without FDS. Therefore, our constant result reveals a fundamental limit of the single-copy measurements, and provides a common framework for studying other interesting quantities for a bipartite quantum state, such as the positivity of the partial transposition and k-symmetric- extendibility [18] .
2. Results
We discuss the constant result, claiming that it is impossible to determine universally whether a given state is entangled or not without FDS, with single-copy measurements. We first prove a no-go theorem for the non- adaptive measurements, and then examine protocol with adaptive measurements as proposed in detail in [19] . We develop an experiment in order to apply this adaptive protocol, and we demonstrate that the information collected is really sufficient for reconstruction of the state.
Non-adaptive measurement. For any given bipartite state рАВ, is allowed only measurement of the physical observables of one copy of this given state. I.e. we can only measure the Hilbert’s operators SK, which act on A⊗B. For simplicity, we consider the case in which both А, В, are qubits. Our method naturally includes also the general case of any bipartite system (see “Additional information” for details).
Now we are looking at a two-qubit state рАВ. To obtain information on р, we measure a range of S physical observables . The informationally full range of observables contains k = 15 linearly regardless of S1. A simple selection of S is the set of all two-qubit matrices of Pauli, except identical with i, j = 0, 1, 2, 3, where s0 = I, s1 = X, s2 = Y, s3 = Z and (i, j ≠ (0, 0).
. The informationally full range of observables contains k = 15 linearly regardless of S1. A simple selection of S is the set of all two-qubit matrices of Pauli, except identical with i, j = 0, 1, 2, 3, where s0 = I, s1 = X, s2 = Y, s3 = Z and (i, j ≠ (0, 0).
Let’s suppose that we can solve universally whether a random рАВ is entangled or not, without a measurement of informationally-complete range of observables. I.e. there is a set S of almost к = 14 physical observables such that, as we measure S, we can say whether рАВ is entangled or not. For this purpose, it is sufficient to assume that к = 14.
The set of all two-qubit states рАВ, designated with А, is characterized with 15 real parameters, which form a convex set in R15. The separable two-qubit states S form a convex subset A. It is common knowledge that S has non-vanishing volume [20] [21] . We designate the set of entangled states with Е. i.e. Е = А/S.
The set of measurements S with k = 14 may be rendered as a definition of the projections of A (and hence of S) on a 14-dimensional hyperplane. If the measurement of the observables in S can demonstrate with certainty whether рАВ is entangled or not, the images on the hyperplane of the separable states S and the entangled state Е should not overlap. We illustrate this geometric idea in Figure 1.
In fact, the only possibility to separate any set from the other states without FDS is the set of the intersection of the set of all states (i.e. set A as in Figure 1) with a generalized cylinder (i.e. a set of the form W (-¥, +¥), where W is a convex set of dimension 14). In this sense, we call these sets “cylindrical”, where the relevant states can be separated from the other states from a projection with 14 (or less) dimensions.
So to show that the detection of entanglement without diagnostics is impossible, it is sufficient to prove that S is not “cylindrical” (at R15). To do this, we show that for each projection on the hyperplane with 14 dimensions with normal direction R, there always is a two-qubit state р, which is on the border of the set S, as R + tR is entangled for some t (see “Additional information” for details). i.e. р and р + tR have the same image of the hyperplane with 14 dimensions.
To be useful, the quantum computers ultimately must include a large number of qubits. At the same time the scientists studying mainly the quantum physics aim at examining larger and larger objects. For example, an entanglement of up to fourteen ions or eight photons has been generated and checked. However, strictly analyzing the quantum properties of these entangled states in these expanded systems with instruments, which are available is cumbersome, mostly because of difficulties like time consuming and difficult data processing. To overcome these restrictions, we need innovative techniques for the analysis of the quantum state. A possible approach is the testing of an entanglement in a range of previously unexplored quantum systems.
Because of their non-local structure, the entanglement witnesses may not directly be provided from local measurements, but it is still easy to obtain the expectation value: Several types of correlations between the quantum systems can simply be measured and then by a linear combination are retrieved the mean values for calculating the value of non-local observables. These ratios may take the form of experimental measurements of polarization on spatially separated photons, where the ratios may be such that two photons will always have opposite polarization. Geometrically, the set of all separable states is convex, which means that for any two points in it, the line for connection is also in the set. This means that can be found such entanglement witnesses W for any entangled state, since there is always a possibility for separation of entangled from the separable states.
This geometric picture leads to a common framework for studying the detection of other interesting quantities for the bipartite quantum state with single-copy measurements. Indeed, our proof also showed that the states sets with positive partial transposition (PPT) are not “cylinder-like”, and it follows herefrom that they cannot be
![]()
Figure 1. Geometry of the separable and entangled states. In the upper part of the space of all matrices is the multitude of all quantum states (light blue), the nonentangled states, forming a convex subset (dark blue).
detected by single-copy measurements without full diagnostics of the state. With a similar method, we can show that the states sets allowing k-symmetric-extendibility, are also not “cylinder-like”, even for a two-qubit system. This shows the fundament limit of the single-copy measurements, i.e., a full diagnostics of the state is required in order to universally reveal the non-trivial properties of the quantum states (i.e. separability, PPT, k-symm- etric-extendibility, see “Additional information” for details).
Adaptive measurement. In case of adaptive protocols, the observable, which must be measured at each step may depend on the previous study results. The type of protocol for measurement may be formulated as follows. First, the observable Н1 is selected, and tr(H1p) is measured. Let’s suppose that the result of the study is α1. On the basis of α1, the observable Н2α1 is selected and tr(Н2α1 p) is measured. Let’s assume that the outcome of the survey is α2. On the basis of α1, α2, the observable Н3α1α2, is selected tr( Н3α1α2 р), is measured and so on.
The protocol in [13] , which should determine the concurrence [15] of a two-qubit state without FDS, falls within the category of adaptive measurements. We implement this protocol and show that with the experimental data collected for a given state рАВ, this protocol does not actually lead to FDS of рАВ. i.e., this protocol does not lead to universal entanglement detection without FDS.
Let’s first briefly introduce the idea for distillation of the entanglement by guiding filtering procedure (33). For unknown two-qubit state , we measure the local reduced matrices of the density
, we measure the local reduced matrices of the density 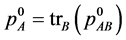 and
and 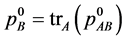 for both qubits. In case that
for both qubits. In case that 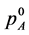 and
and  are not fully mixed, we produce the first filter
are not fully mixed, we produce the first filter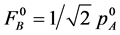 , on the basis of the information for
, on the basis of the information for 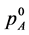 and change
and change  to
to . In a similar way, the same procedure is repeated for qubit В. The iterative applications of the filter continue and at step k, the reduced matrices of the density of the qubits will be
. In a similar way, the same procedure is repeated for qubit В. The iterative applications of the filter continue and at step k, the reduced matrices of the density of the qubits will be 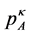 and
and .
.
In case that  and
and ![]() are not identity, the iterative procedure described above leads to a “distillation” of the matrices
are not identity, the iterative procedure described above leads to a “distillation” of the matrices ![]() and
and ![]() and it is ensured that both merge into one identity. All of the reduced matrices of the density
and it is ensured that both merge into one identity. All of the reduced matrices of the density ![]() and
and![]() . (
. (![]() ) are recorded at the time of the iterative procedure. At step k, when
) are recorded at the time of the iterative procedure. At step k, when ![]() and
and ![]() almost reached the identity, they may be used to reconstruct the boundary of the entanglement value in
almost reached the identity, they may be used to reconstruct the boundary of the entanglement value in ![]() through the optimum witness W (
through the optimum witness W (![]() ), which depends only on
), which depends only on ![]() and
and![]() . (
. (![]() ) (up to local uniform transformation), whose value says whether
) (up to local uniform transformation), whose value says whether ![]() is entangled or not [13] .
is entangled or not [13] .
At first glance, the above procedure seems acceptable to determine the entanglement value without FDS because only the single-qubit matrices of the density ![]() and
and![]() . (
. (![]() ) are measured for the second time and only local uniform transformations are used for the construction of the optimal witness. i.e. it appears that the two-qubit correlations of
) are measured for the second time and only local uniform transformations are used for the construction of the optimal witness. i.e. it appears that the two-qubit correlations of ![]() are never measured, which does not lead to FDS. But more detailed examination shows that this is not the case. The key observation is that the “local” filters in fact are “weak” measurements, which record the correlations in
are never measured, which does not lead to FDS. But more detailed examination shows that this is not the case. The key observation is that the “local” filters in fact are “weak” measurements, which record the correlations in![]() . This is because the filters cannot be applied with a probability of one, so that the correlation in
. This is because the filters cannot be applied with a probability of one, so that the correlation in ![]() is “encoded” in the information that all filters are applied successfully. In other words, what the local filters and the local diagnostics make on each qubit, is in fact a FDS of
is “encoded” in the information that all filters are applied successfully. In other words, what the local filters and the local diagnostics make on each qubit, is in fact a FDS of![]() .
.
To demonstrate the relationship between the local filters and FDS, we simulate a procedure with a local filter as we choose another number of applied filters. It appears that in many cases k = 4 (five filter) is sufficient in order to uniquely determine ![]() on the basis of
on the basis of ![]() and
and![]() . (
. (![]() ). So the information of
). So the information of ![]() and
and![]() . leads to FDS of
. leads to FDS of![]() .
.
As an example, we illustrate the simulation of the input state as equation (5) with l = 0.2. Initially, we have 15 real parameters (i.e. degrees of freedom, DOF for short), which to determine ![]() (by ignoring the part of the identity, due to the condition of the normalization). When applying more and more filters, DOF is reduced finally because we obtain more information for the original input state. For example, the initial local reduced matrices of the density
(by ignoring the part of the identity, due to the condition of the normalization). When applying more and more filters, DOF is reduced finally because we obtain more information for the original input state. For example, the initial local reduced matrices of the density ![]() and
and ![]() before the application of any filter can reduce DOF up to 9;
before the application of any filter can reduce DOF up to 9; ![]() after the first filter imposes more restrictions so that DOF reduces to 6, etc. It is proven that with 5 filters the input state
after the first filter imposes more restrictions so that DOF reduces to 6, etc. It is proven that with 5 filters the input state ![]() may be determined uniquely through the information gathered on the reduced matrices of density. And this procedure works in a similar way for many other two-qubit states
may be determined uniquely through the information gathered on the reduced matrices of density. And this procedure works in a similar way for many other two-qubit states![]() , where 5 filters are sufficient to reconstruct
, where 5 filters are sufficient to reconstruct![]() , which we will show later in the results of the experiments.
, which we will show later in the results of the experiments.
Experimental protocol in the setup of nuclear magnetic resonance. In order to apply experimentally the protocol, we first must discuss how to realize the local filters at a NMR system. Without loss of generality, we can look at the local filter FA applied on qubit A for example. For any FA, it may always be decomposed to the form UAΛAVA through decomposition of the only value where UA and VA are inseparable values and ΛA is the diagonal operator of Kraus:
![]() (1)
(1)
![]() relies on FA and indicates the probability that the excited state
relies on FA and indicates the probability that the excited state ![]() to be decomposed to the ground state
to be decomposed to the ground state![]() , when the system undergoes ΛA. Although it is not inseparable, ΛA may be extended up to a two-qubit unitary with the assistance of the ancilla qubit 1. Basically, if a two-qubit unitary can transform
, when the system undergoes ΛA. Although it is not inseparable, ΛA may be extended up to a two-qubit unitary with the assistance of the ancilla qubit 1. Basically, if a two-qubit unitary can transform
![]() (2)
(2)
the quantum channel of the system qubit A, will be ΛA. By selecting later the subspace, where the ancilla qubit ![]() is. One possible unitary transformation, which satisfies the equation (2) is
is. One possible unitary transformation, which satisfies the equation (2) is
![]() (3)
(3)
The operation U1A in this way is a controlled rotation: when the qubit of the system А is![]() , the ancilla remains invariant; when А is
, the ancilla remains invariant; when А is![]() , the ancilla undergoes a rotation Ry (0A) = ei0τy/2, where
, the ancilla undergoes a rotation Ry (0A) = ei0τy/2, where![]() . Therefore, in a system with ancillaries, when initiating the ancilla with
. Therefore, in a system with ancillaries, when initiating the ancilla with![]() , the local filter FA may be implemented through a two-qubit gate (I⊗UA)1A(I⊗VA) followed by post-selection of a subspace, in which the ancilla is
, the local filter FA may be implemented through a two-qubit gate (I⊗UA)1A(I⊗VA) followed by post-selection of a subspace, in which the ancilla is![]() .
.
The schematic circuit for the application of a proposal for a filter-based distillation of the entanglement for an unknown two-qubit state![]() .
. ![]() (i ≥ 0) is i local filter, applied to A and B, where
(i ≥ 0) is i local filter, applied to A and B, where ![]() and
and![]() . A single-qubit diagnostic is applied. A variation is simulated of concurrence and fidelity by increasing the number 1 ≤ m < 6 of the applied filters. The simulated state is selected as equation Λ = 0.2 For any given m, we collected all available reduced matrices of the density at this stage and reconstructed 100 likely input states. When m ≤ 4, the reconstructed state is not unique because of the absence of restrictions, so that both the concurrence and fidelity have known distributions. When m = 5, the input state may be uniquely defined and the concurrence and fidelity merge into one point.
. A single-qubit diagnostic is applied. A variation is simulated of concurrence and fidelity by increasing the number 1 ≤ m < 6 of the applied filters. The simulated state is selected as equation Λ = 0.2 For any given m, we collected all available reduced matrices of the density at this stage and reconstructed 100 likely input states. When m ≤ 4, the reconstructed state is not unique because of the absence of restrictions, so that both the concurrence and fidelity have known distributions. When m = 5, the input state may be uniquely defined and the concurrence and fidelity merge into one point.
Application of NMR. In order to implement the abovementioned protocol based filter of the distillation of the entanglement in NMR, we need a 4-qubit quantum processor, which shall consist of two system qubits A and B and two ancilla qubits 1 and 2. Our 4-qubit sample is 13С with trans-crotonic acid, dissolved in d6-acetone. The Methyl-group М, Н1 and Н2 are distinguished through all experiments. The internal operator of Hamilton of this system may be described as
![]() (4)
(4)
where υj is the chemical change of the j-th rotation and Jjk is the J-th strength of the connection between rotations j and k. We denoted C3 and С2 as the system qubits A and B, and C4 and С1 as ancilla qubits 1 and 2 which can help at in imitating the filters, respectively. All experiments were carried out on a Bruker DRX 700MHz spectrometer at room temperature.
Our target input state was selected as a combined state, including one proportion of the state of the Bell and two proportions of the state of the product, as the state of the Bell can be adjusted. This state is written as:
![]() (5)
(5)
where
![]() (6)
(6)
have matches 1, 0 and 0 respectively. The parameter λ in (0.1) is thus proportional to the entanglement value![]() . In the experiment, we varied with λ from 0.2 to 0.7 with a step with size 0.1 for each point and implement the relevant proposal. As we take into account the two ancilla, the overall input state of our 4-qubit system thus is
. In the experiment, we varied with λ from 0.2 to 0.7 with a step with size 0.1 for each point and implement the relevant proposal. As we take into account the two ancilla, the overall input state of our 4-qubit system thus is![]() . We prepared a pseudo-pure state through average spatial technique, and then we created the three components
. We prepared a pseudo-pure state through average spatial technique, and then we created the three components![]() ,
, ![]() and
and ![]() on the system qubits, respectively. As a result, each component undergoes the whole filtering and the stage of reading of the single qubit, as the final result is obtained by a summary of all three experiments.
on the system qubits, respectively. As a result, each component undergoes the whole filtering and the stage of reading of the single qubit, as the final result is obtained by a summary of all three experiments.
A sequence of NMR, which to realize the proposal based on filter, for the distillation of the entanglement. More precisely, this sequence shows how to realize the first two filters ![]() and
and ![]() regarding the terms of NMR pulse. All other sequences can be obtained in an analogous manner. The first 4-qubit system is prepared for positive partial state (PPS) by the average spatial technique that is applied before the step of starting. Then, the system qubits are started to
regarding the terms of NMR pulse. All other sequences can be obtained in an analogous manner. The first 4-qubit system is prepared for positive partial state (PPS) by the average spatial technique that is applied before the step of starting. Then, the system qubits are started to![]() ,
, ![]() and
and ![]() by three independent experiments. The part after the step of the starting is a sequence for realization of the filters. VA, VB, UA, UB, θ1 and θ2 all depend on the measured results of the reduced matrices of density.
by three independent experiments. The part after the step of the starting is a sequence for realization of the filters. VA, VB, UA, UB, θ1 and θ2 all depend on the measured results of the reduced matrices of density.
The two-qubit diagnostics of the state is applied on the system qubits after the creation of![]() .
. ![]() was reconstructed in the experiment and its fidelity compared to the expected
was reconstructed in the experiment and its fidelity compared to the expected ![]() is above 98% for any λ. This two-qubit diagnostics of the state is not required in the initial proposal in which are necessary measurements with only single qubit. But as we claim that the proposal based on filter already has provided sufficient information to reconstruct the initial two-qubit state
is above 98% for any λ. This two-qubit diagnostics of the state is not required in the initial proposal in which are necessary measurements with only single qubit. But as we claim that the proposal based on filter already has provided sufficient information to reconstruct the initial two-qubit state![]() , we must compare with
, we must compare with![]() , which is reconstructed after the passing of the entire proposal. To prove our point of view, we must show that
, which is reconstructed after the passing of the entire proposal. To prove our point of view, we must show that ![]() and
and ![]() are the same at small errors in the experiments. This comparison is the sole purpose of carrying out the diagnostics of the two- qubit state.
are the same at small errors in the experiments. This comparison is the sole purpose of carrying out the diagnostics of the two- qubit state.
Now we should demonstrate how to realize the local operations for filtering in NMR. By measuring the local reduced matrix of the density ![]() of the input state
of the input state![]() , the first filter is calculated through
, the first filter is calculated through ![]() and is decomposed to
and is decomposed to![]() . Since
. Since ![]() and
and ![]() are simply local unitaries of qubit A, they may be realized through pulsation of a local radio frequency, straightforwardly.
are simply local unitaries of qubit A, they may be realized through pulsation of a local radio frequency, straightforwardly.![]() , which may be extended to a 2-qubit controlled rotation U1A, (see the equation (3)) in a larger space of Hilbert, proceeded by a combination of pulsation of the local radio frequency and evolution of the J-coupling (45).
, which may be extended to a 2-qubit controlled rotation U1A, (see the equation (3)) in a larger space of Hilbert, proceeded by a combination of pulsation of the local radio frequency and evolution of the J-coupling (45).
![]() (7)
(7)
where ![]() is the evolution of the J-coupling e−iθAσz σz/4 between the qubits 1 and A and
is the evolution of the J-coupling e−iθAσz σz/4 between the qubits 1 and A and
![]() , which depends from
, which depends from![]() . After this filter, the system is changed to
. After this filter, the system is changed to![]() , and a diagnostics with single qubit was applied, The same procedure is repeated for a qubit B, in order to realize the second filter
, and a diagnostics with single qubit was applied, The same procedure is repeated for a qubit B, in order to realize the second filter![]() . In the experiment, these two filters
. In the experiment, these two filters ![]() and
and ![]() are applied at the same time by using the technique of partial decoupling, with additional Z rotations to the end in order to be compensated the unwanted phases, caused by the evolution of the chemical changes. The pulses are used for realizing R1 y(qA/2) and R2 y(qB/2), respectively, and the free time of evolution τ1 and τ2 are defined as
are applied at the same time by using the technique of partial decoupling, with additional Z rotations to the end in order to be compensated the unwanted phases, caused by the evolution of the chemical changes. The pulses are used for realizing R1 y(qA/2) and R2 y(qB/2), respectively, and the free time of evolution τ1 and τ2 are defined as
![]() (8)
(8)
Here we have assumed that t2 > 0 (![]() ). When τ2 < 0, the circuit needs to be slightly modified by adjusting the positions of refocusing of the π pulses. All other filters have similar structures and they are always applied on qubit A and B simultaneously from their beginning.
). When τ2 < 0, the circuit needs to be slightly modified by adjusting the positions of refocusing of the π pulses. All other filters have similar structures and they are always applied on qubit A and B simultaneously from their beginning.
Every time after executing one local filter, we implement diagnostics with single qubit on the other qubit, rather than the working qubit at which was applied the filter. The reason is that the working qubit has developed to identity due to the properties of this filter. The tomographic result was used for development of the next filter on the other qubit. In principle, before the application of any filters, it is necessary to be set the two ancilla qubits to![]() . Since it is difficult to be loaded again the rotations in NMR, in our experiments was adopted an alternative way. For example, to realize
. Since it is difficult to be loaded again the rotations in NMR, in our experiments was adopted an alternative way. For example, to realize![]() , we bind it with
, we bind it with![]() , and generate a new operator. It can be seen as 2 in 1 filter and to be applied in the same way. Thus we avoided the resetting of the operations during the experiments and for any separate experiment, we simply start from the original two-qubit state
, and generate a new operator. It can be seen as 2 in 1 filter and to be applied in the same way. Thus we avoided the resetting of the operations during the experiments and for any separate experiment, we simply start from the original two-qubit state![]() . These operations based on the feedback continue to be executed until 5 filters applied and seven 1-qubit tomographies performed.
. These operations based on the feedback continue to be executed until 5 filters applied and seven 1-qubit tomographies performed.
From the above discussions, we showed that the experiments with NMR contain only evolution of free J-couplings and unitaries with single qubit. For the evolutions of the J-couplings, we imposed in the system to be applied free equation of Hamilton (4) for the same time. For local unitaries, we use techniques for Gradient Ascent Pulse Engineering (GRAPE), in order to optimize them (46), (47). The method GRAPE provides 1 ms width of the pulse and above 99.8% fidelity for each local unitary, and furthermore all pulses are corrected by setup of the control of the feedback in NMR spectrometer in order to reduce the contradictions between the ideal and the applied pulses (48)-(50).
Experimental results and analysis of errors. We prepared six input states by varying λ from 0.2 to 0.7 with 0.1 size of the step in the form of equation. After the preparation, we carried out two-qubit full diagnostics of the state for each state, and reconstructed them as![]() , where the exponent means experiment. The fidelity between the theoretical state
, where the exponent means experiment. The fidelity between the theoretical state ![]() and the measured state
and the measured state ![]() is above 99.2% for each of the six input states. The fidelity can be attributed to the deficiencies of PPS, GRAPE pulses and the effect of low decoherence. However this fidelity is only used to assess the accuracy of the preparation of our input state. For the last experiments, we only compared the experimental results with
is above 99.2% for each of the six input states. The fidelity can be attributed to the deficiencies of PPS, GRAPE pulses and the effect of low decoherence. However this fidelity is only used to assess the accuracy of the preparation of our input state. For the last experiments, we only compared the experimental results with![]() , as
, as ![]() was the actual state from which we have started the experiment based on the filter.
was the actual state from which we have started the experiment based on the filter.
After the initial preparation of the state and each filter we received the reduced matrix of the density of qubit A and/or B through diagnostics of single qubit in the subspace, where the ancillary qubits are ![]() (see “Methods”). The average fidelity between the measured state with single qubit and the expected state, calculated with
(see “Methods”). The average fidelity between the measured state with single qubit and the expected state, calculated with ![]() is about 99.6% (“Additional table” S1), which demonstrates that our filtering operations and tomographies with single qubit are accurate.
is about 99.6% (“Additional table” S1), which demonstrates that our filtering operations and tomographies with single qubit are accurate.
The Fidelities between ![]() and
and ![]() for various λ-s.
for various λ-s. ![]() is obtained from the diagnostics of two-qubit state immediately after the creation of the input state
is obtained from the diagnostics of two-qubit state immediately after the creation of the input state![]() , and
, and![]() , of the maximum probability for recreating
, of the maximum probability for recreating![]() , on the basis of the own seven states with single qubit. The bar of the errors comes from the relevant uncertainty when extracting the NMR spectrum in the quantum states. All fidelities are above 93.0%, which means that the initial two-qubit state can be reconstructed only by seven states with single qubit.
, on the basis of the own seven states with single qubit. The bar of the errors comes from the relevant uncertainty when extracting the NMR spectrum in the quantum states. All fidelities are above 93.0%, which means that the initial two-qubit state can be reconstructed only by seven states with single qubit.
With seven states with single qubit, we can recreate the initial two-qubit state![]() . Here was applied the method for maximum probability and we came to the conclusion that
. Here was applied the method for maximum probability and we came to the conclusion that ![]() is the closest to the experimental raw data. Quite surprisingly,
is the closest to the experimental raw data. Quite surprisingly, ![]() is very similar to
is very similar to ![]() and the fidelity between them for each λ is above 92%. The experimental results clearly show that the information of the seven states with single qubit collected at the time of the procedure for the distillation of the entanglement based on filters, facilitates the recreation of the initial two-qubit state. In other words, this proposal based on the filter to universally detect and distill the entanglement is equivalent compared to the conduct of diagnostics with two-qubit state.
and the fidelity between them for each λ is above 92%. The experimental results clearly show that the information of the seven states with single qubit collected at the time of the procedure for the distillation of the entanglement based on filters, facilitates the recreation of the initial two-qubit state. In other words, this proposal based on the filter to universally detect and distill the entanglement is equivalent compared to the conduct of diagnostics with two-qubit state.
Then we calculated the concurrence for each one of the cases with different input two-qubit state. The concurrence is monotone entanglement defined for combined state p of two qubits
![]() (9)
(9)
where l1, l2, l3 и l4 are the own values of
![]() (10)
(10)
in descending order. Obviously, the concurrence is proportional to the λ, as the λ is the weight of the state of the Bell, which is the only thing, which contributes to the entanglement. The blue squares show the concurrence of![]() , the state obtained by the diagnostics of the two-qubit state on the experimentally prepared state. Recall that the preparation of the fidelity is always 98.2% so the blue squares do not deviate much from the brown curve. The red circles show the concurrence of
, the state obtained by the diagnostics of the two-qubit state on the experimentally prepared state. Recall that the preparation of the fidelity is always 98.2% so the blue squares do not deviate much from the brown curve. The red circles show the concurrence of![]() , which in the ideal case must be the same as the blue squares if there are no experimental errors. But in the experiment there are unavoidable errors caused by many factors such as the imprecision of the stage of reading the single qubit, the imperfect application of the filters and the relaxation, and we must take them into account.
, which in the ideal case must be the same as the blue squares if there are no experimental errors. But in the experiment there are unavoidable errors caused by many factors such as the imprecision of the stage of reading the single qubit, the imperfect application of the filters and the relaxation, and we must take them into account.
For convenience, we assume that the errors come from three main aspects and are additive. One error is caused by the inaccuracy of the procedure of the diagnostics with single qubit. As we used the least-square fitting algorithm to analyze the spectrum of the outcome, and we have converted the data into quantum states, the concurrence caused around 3.00% uncertainty of the final result with single qubit. The second is the error from the application of imperfect filters in the experiment. It originates mainly from errors in the accumulation of GRAPE pulses, which is about 1.59% for each operation of the filter. The third error, to a lesser extent, was around 1.20%, caused by decoherence. Therefore, in total we have concluded that at most 5.79% error may appear in the whole process. We identified them as artificial noise and we’ve incorporated them in the theoretical input state![]() . In the simulation, we first discretized λ to 200 values from λ = 0.1 to λ = 0.8. For a given λ 2500 states were randomly calculated as deviation from
. In the simulation, we first discretized λ to 200 values from λ = 0.1 to λ = 0.8. For a given λ 2500 states were randomly calculated as deviation from ![]() within the 5.79% range of the noise. For each specified state the concurrence was calculated and projected onto one point. From here, a color space was generated, taking into account the density of the points. All of our experimental results fall within that space, which is consistent with the simulation of the model.
within the 5.79% range of the noise. For each specified state the concurrence was calculated and projected onto one point. From here, a color space was generated, taking into account the density of the points. All of our experimental results fall within that space, which is consistent with the simulation of the model.
3. Conclusion
We proved the no-go theorem, and that there is no way to detect the entanglement of an arbitrary bipartite state рАВ without FDS if only nonadaptive measurements with one copy are allowed. Our conclusion follows from a good geometric picture: It is not possible to detect a projection of the space of the state on a lower hyperplane of the dimension with non-overlapping image for a set of separable states and entangled states. Our method provides a common framework for studying the detection of other interesting quantities for the bipartite quantum state, such as positive partial transposition and k-symmetric-extendibility. We also have analyzed the case of the adaptive measurements. It is assumed in (33) that the concurrence in the measurement of the entanglement for two-qubit states can be determined without FDS, through measurements with single copy. In order to apply this protocol, we have developed a method with maintaining of ancillaries to finalize the filters. Practically, the technique can be extended to cover other quantum systems, except the optics in order to apply a channel reducing the amplitude that is of enormous importance in the quantum information. Through the application of this protocol, we show that when the experimental data are collected for a given state рАВ, this protocol leads in fact to FDS of рАВ. Therefore, this protocol does not lead to universal detection of рАВ without FDS.
Concurrence of![]() ,
, ![]() and
and ![]() as a function of the weight of the state of Bell λ. The concurrence is calculated for the theoretical state
as a function of the weight of the state of Bell λ. The concurrence is calculated for the theoretical state ![]() and displays the value of the concurrence as a monotonically increasing function of λ. The concurrence of
and displays the value of the concurrence as a monotonically increasing function of λ. The concurrence of![]() , the state is obtained from the diagnostics of the two-qubit state immediately after the preparation of the input state. In total, we roughly can suppose that this state is truly prepared state, and that the following operations of the filters are always applied to this state as long as we do not neglect the measurement of the errors at the reconstruction of
, the state is obtained from the diagnostics of the two-qubit state immediately after the preparation of the input state. In total, we roughly can suppose that this state is truly prepared state, and that the following operations of the filters are always applied to this state as long as we do not neglect the measurement of the errors at the reconstruction of![]() . The concurrence of
. The concurrence of ![]() the state is reproduced with seven states with single qubit. In the ideal case,
the state is reproduced with seven states with single qubit. In the ideal case, ![]() and реf must be one and the same if there are no experimental errors. The artificial noise is with a strength of 5.89%, which is roughly calculated from the coincidence of the errors up to 3%. The GRAPE imperfection error is 1.49 and the error upon decoherence is 1/21%. We have added this noise to the theoretical state
and реf must be one and the same if there are no experimental errors. The artificial noise is with a strength of 5.89%, which is roughly calculated from the coincidence of the errors up to 3%. The GRAPE imperfection error is 1.49 and the error upon decoherence is 1/21%. We have added this noise to the theoretical state
![]() and randomly provided 2400 states within the range of the noise for each λ (200 values in [0.1, 0.9]. The defined places thus are based on the density of the projected points of 2400.
and randomly provided 2400 states within the range of the noise for each λ (200 values in [0.1, 0.9]. The defined places thus are based on the density of the projected points of 2400.
This justifies our unchanging results, which indicates that even when at the adaptive measurements, the universal entanglement detection by measurements with single-copy is impossible without FDS.
It is important to underline that the large identity does not arise at any unitary propagator and it is not observed in NMR. So there is only a need for focusing on the part for the deviation |0000>, as the entire system is functioning exactly as it.
In consequence, each component undergoes the entire procedures for filtering and measuring respectively, as the final result is obtained by summarizing all three experiments.
Diagnosis with single qubit after each filter. The procedure for the distillation of the entanglement described to in Ref. (33), includes local filtering operations, which means that each filter depends on the previous result from the measurement with single qubit. In one experiment, we performed diagnostics with single qubit on the system qubits C2 and С3, respectively. It requires measurement of the expected values of sx, sy and sz, respectively. In our 4-qubit system, this diagnostics with single qubit (as we assume the measurement of is equal to the measurement ![]() ⊗sx, y, z ⊗ I ⊗
⊗sx, y, z ⊗ I ⊗ ![]() , as we must be focusing on the subspace where the ancilla qubits are
, as we must be focusing on the subspace where the ancilla qubits are![]() . In order to obtain the expected values of the observables, a procedure for fitting the spectrum must be applied in order to extract these results from the spectrum of NMR.
. In order to obtain the expected values of the observables, a procedure for fitting the spectrum must be applied in order to extract these results from the spectrum of NMR.
So our survey shows the fundamental ratio between the detection of the entanglement and the diagnostics of the quantum state. Namely that universal entanglement detection without FDS is not possible only with single-copy measurements. Naturally occurs also the question of whether the joint measurements on r copies of the state ![]() (i.e. р ⊗rАВ) for r > 1 are allowed. In this case, indeed the entanglement may be detected universally for any
(i.e. р ⊗rАВ) for r > 1 are allowed. In this case, indeed the entanglement may be detected universally for any ![]() without to reconstruct the state, and one example for defining the concurrence of the two-qubit
without to reconstruct the state, and one example for defining the concurrence of the two-qubit ![]() is given in (22)-(24). But, the Protocol (23) includes joint measurements on 4 copies of
is given in (22)-(24). But, the Protocol (23) includes joint measurements on 4 copies of ![]() (i.e. р ⊗rАВ), which makes it difficult to be implemented in practice. It would be interesting to find a smaller r such that the joint measurements of с are sufficient for the universal detection of the entanglement of рАВ without full diagnostics of the state.
(i.e. р ⊗rАВ), which makes it difficult to be implemented in practice. It would be interesting to find a smaller r such that the joint measurements of с are sufficient for the universal detection of the entanglement of рАВ without full diagnostics of the state.
In fact there are also cases in which this is possible even for r = 2. For example, we found such a scheme, which reveals the entanglement of an arbitrary two-qubit state рАВ without FDS, if we allow joint measurements of two copies. The idea is that рАВ is entangled only and only when (23) Det (![]() ) <0, where
) <0, where ![]() is partial transposition of рАВ of the system A. Thus we must only design a scheme with measurement of р ⊗rАВ, which may give the value of Det (
is partial transposition of рАВ of the system A. Thus we must only design a scheme with measurement of р ⊗rАВ, which may give the value of Det (![]() ). This really can be done without FDS.
). This really can be done without FDS.
Furthermore, if only measurements with single-copy are permitted, the value of Det (![]() ), cannot be determined, even with adaptive measurements. Let’s suppose that similar adaptive measurements exist. Now we assume that the input state is maximal mixed state I/4, after measurement, and thus we can calculate the determinant. Please note that there is at least one traceless R other than zero, which is not measured, which means that these measurements cannot make a distinction between I/4 and I/4 + tr. Therefore, Det (I/4 + tRr) = Det (I/4) for small enough R = 0.
), cannot be determined, even with adaptive measurements. Let’s suppose that similar adaptive measurements exist. Now we assume that the input state is maximal mixed state I/4, after measurement, and thus we can calculate the determinant. Please note that there is at least one traceless R other than zero, which is not measured, which means that these measurements cannot make a distinction between I/4 and I/4 + tr. Therefore, Det (I/4 + tRr) = Det (I/4) for small enough R = 0.