Improved PLL Tuning of Shunt Active Power Filter for Grid Connected Photo Voltaic Energy System ()
Received 20 May 2016; accepted 28 May 2016; published 19 August 2016

1. Introduction
In recent years, power quality at end user’s terminal is affected greatly and it has become a great concern in many industrial applications. Therefore, it is very essential to identify novel and efficient system that would mitigate the disturbances in the electrical systems, improving their power quality [1] . Normal filters such as LC, LCL, etc., are used to eliminate specified frequency range and thus, it can be only used for predetermined loads. Thus, Active Power Filter (APF) has been used for these types of harmonic mitigation concerns in transmission lines [2] .
Shunt active power filter has the growing popularity than series active power filter since most of the industrial applications require the compensation towards current harmonics. It has the ability to keep the current in the source as balanced and sinusoidal after compensation, irrespective of whether the load is nonlinear, balanced or unbalanced [3] - [5] . The utilization of SAPF provides significant advantages to the power system. Thus, developing new methodologies have become an active area of research to improve the performance of these SAPFs [6] .
In recent decades, interconnection of Renewable Energy Sources (RES) with SAPF has become one of the attractive research topics. But, there is a certain level of influence and impact that renewable generation has on power quality on account of its nonlinearity, especially as both solar generation plants as well as wind power generators have to be connected as such with the grid using high power static Pulse Width Modulated (PWM) converters [7] . Power generation in non uniform nature has a direct effect on the voltage that is regulated therein and thus leads to voltage distortion in power systems. This paper focuses on contributing an efficient compensation technique to deal with the problem of power quality disturbances in the power distribution systems due to the RES interconnection.
Many types of active power filter configurations have been proposed in the last two decades to achieve the required harmonic compensation level. The main techniques in the active filter are to generate the reference current and the control method applied to inject the required compensation current into the line, which decides the performance of an active filter. There are several methods for reference current generation for the shunt active power filters. In 1984, H. Akagi stated instantaneous active and reactive power theory control method that was quite efficient method for three phase loads in the balanced system, being later worked by Watanabe and Aredes for three phase four wire systems; later F.Z. Peng proposed zero sequence currents. Synchronous Reference Frame (SRF) concept is simple algorithm having good dynamic responses. The SRF could compensate the harmonics in the current and reactive power component from the distorted load currents.
In 1995, Bhattacharya proposed dq component’s calculations of the instantaneous three phase currents and created synchronous reference frame concept. A dq based current reference generator scheme is used to obtain the reference current signal of the active power filter. This scheme presents a fast and accurate signal tracking capability, which avoids voltage fluctuations that deteriorate the current reference signal affecting compensation performance [8] . So, in this work, dq based current reference generator scheme is preferred.
To implement the dq based current reference generator, some kind of synchronizing system should be used. PLL has been widely used for the synchronization purpose. SRF-PLL has been widely used in power system applications due to its simplicity and considerable performance. But it suffers from double frequency error when the input signal is unbalanced. Moreover, it also has drawbacks due to the presence of DC components. The DC component can be an intrinsic component of a signal (e.g., the DC link voltage in a single phase rectifier that has a DC and a second order harmonic), and can be generated by measurement devices (e.g., due to the saturation phenomenon in a current transformer [9] ), conversion processes (e.g., the A/D conversion for fixed point DSP applications [10] ), or when a fault occurs [11] . Therefore, it is necessary to remove any error that such a component may cause. But, complete removal of DC component in the PLL systems has not been addressed in the literature so far [12] .
In this paper the author proposed a method to address the DC component in the input signal of the PLL and notch filter algorithms for filtering and synchronization applications. This paper takes the motivation of the abovementioned work and focuses on improving the performance of the overall system through the utilization of swarm intelligence optimization algorithm.
Traditional PI controllers are widely used in the control loop of the voltage source converters to produce the switching states of the converters because of its simplicity in control design. Perfect tuning of the controller is needed to have the satisfactory operation of the converters and several traditional tuning rules, such as Ziegler and Nichols, Astrom and Hagglud, Sain and Ozgen cohen and coon etc. are adopted for this purpose. Though they are enough for the first order system, they produce large overshoot and required repeated design process for any variations in the system model. But in general the power system has many disturbances, parameter variations and has many nonlinear loads which lead to the degradation of the quality of the power. Hence the continuous tuning algorithm is needed to have satisfactory operation in its dynamic nature [13] - [16] . Hence this paper brings out the unique optimized self tuning of the controller for the PLL structure in the current control loop of the VSCs, which is obtained by ABC algorithm.
The main contribution of this paper is to tune the PLL block parameters such as proportional gain (Kp), integral gain (Ki) , change in the instantaneous frequency (Ko) and voltage magnitude gain (Kv) . The settling time and the steady state response of the frequency are tuned by Ki and Kp gain values. Similarly, elimination of DC component and identification of the voltage magnitude are tuned through Ko and Kv gain values through the ABC optimization approach. Moreover, the control loop of Voltage Source Inverter (VSI) is proposed with the predictive current control approach. This method predicts the future load current values for the voltage vectors generated by the inverter. The voltage vector which minimizes a cost optimization function is selected. The cost optimization function used in this work evaluates the error current at the next sampling time. In order to select the optimal switching state that must be applied to the power converter, ABC optimization is used in this work which selects the best minimal optimal value “g”.
This paper is organized as follows. Section 2 deals with the proposed methodology. Section 3 discusses about the three leg converter model. Section 4 describes about the proposed ABC based predictive current control model. Section 5 narrates about current reference generation. Section 6 validates the simulation results to proof the performance of the proposed system.
2. Proposed Methodology
Figure 1 shows the proposed SAPF system model with RES interconnection. The electrical energy consumption behaviour is an unpredictable, and random in nature. It may be single or three-phase, balanced or unbalanced, and linear or nonlinear. A shunt active power filter is connected at the point of common coupling in parallel to compensate current harmonics, current unbalance, and reactive power [17] . As shown in Figure 1, it is composed by an electrolytic capacitor, a PWM converter and a first order output ripple filter. This circuit utilizes the power system equivalent impedance Zs, output ripple filter impedance Zf of the converter and the impedance ZL of the load. When RES generates excess power than the load demand, then the excess power is given to the grid to maintain the load voltage of frequency constant.
![]()
Figure 1. Shunt active power filter model.
The main element of this system is a voltage source inverter, as it interfaces the renewable energy source to the grid and delivers the generated power. In this work, grid interfacing inverter can effectively be utilized to perform the following important functions: 1) non linear load current harmonics mitigation; 2) unbalanced current compensation in case of 3 phase 3 wire system; 3) ABC based Predictive control technique for cost optimization 4) ABC based PLL tuning approach under unbalanced load conditions. Moreover, with adequate control of grid interfacing inverter, all the four objectives can be accomplished either individually or simultaneously.
3. Three Leg Converter Model
An illustration of converter’s power circuit employed here is presented in Figure 2. Converter topology has similar features to those of traditionally deployed three phase converter that has a three leg system [18] . The switching states of the converter are decided by the gating signals Su, Sv and Sw , as follows in Equation (1):
 (1)
(1)
and Equation (1) can be expressed in vectorial form as in Equation (2).
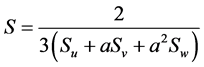 (2)
(2)
where 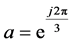 .
.
The output voltage space vectors created by the inverter are defined as in Equation (3)
 (3)
(3)
where  are the phase to neutral (N) voltages of the inverter (Figure 2). Then, the load voltage vector can be related to the switching state vector S as in Equation (4)
are the phase to neutral (N) voltages of the inverter (Figure 2). Then, the load voltage vector can be related to the switching state vector S as in Equation (4)
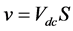 (4)
(4)
where 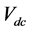 is the DC link voltage.
is the DC link voltage.
Taking in to consideration gating signals combinations of 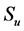 ,
,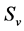 and
and  eight switching states, and as a result, eight voltage vectors are thus obtained. Note that
eight switching states, and as a result, eight voltage vectors are thus obtained. Note that  , which results in only seven different voltage vectors, as shown in Figure 3. Filter’s mathematical model derivation is given in Equation (5).
, which results in only seven different voltage vectors, as shown in Figure 3. Filter’s mathematical model derivation is given in Equation (5).
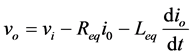 (5)
(5)
where Req and Leq are the 3L-VSI output parameters expressed as Thevenin impedances at the converter output terminals Zeq. Hence, the Thevenin’s equivalent impedance is calculated by a series connection of the ripple filter impedance Zf and the arrangement in parallel between the system equivalent impedance Zs and the load impedance ZL as shown in Equation (6).
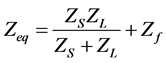 (6)
(6)
For this model, it is assumed that ![]() , and the resistive part of the system’s equivalent impedance is neglected, and the series reactance is considered in the range of 3% - 7% p.u., which is a satisfactory approximation of the real system. Finally, in Equation (5) Req = Rf and Leq = Ls + Lf. For complete understanding the PWM switching time calculation of the inverter switches are given in Table 1.
, and the resistive part of the system’s equivalent impedance is neglected, and the series reactance is considered in the range of 3% - 7% p.u., which is a satisfactory approximation of the real system. Finally, in Equation (5) Req = Rf and Leq = Ls + Lf. For complete understanding the PWM switching time calculation of the inverter switches are given in Table 1.
![]()
Table 1. Switching time calculation of the inverter.
![]()
Figure 3. Voltage vector generated by the inverter.
3.1. Design of DC Link Capacitor
The value of dc link capacitor is chosen from the reference dc voltage, (![]() ) is the maximum voltage level of the dc bus, I is the phase current of VSI,
) is the maximum voltage level of the dc bus, I is the phase current of VSI, ![]() is the angular frequency and (t) time for which dc bus voltage is to be recovered. It is given as in Equation (7).
is the angular frequency and (t) time for which dc bus voltage is to be recovered. It is given as in Equation (7).
![]() (7)
(7)
where ω = 2p ´ 50 = 314.159; Ic(rated) = rated current, ![]()
3.2. Design of Filter Inductance
The amount of filtering inductance to be added to the SAPF is
![]() (8)
(8)
where (![]() ) represents dc link voltage, (
) represents dc link voltage, (![]() ) represents maximum switching frequency, (
) represents maximum switching frequency, (![]() ) represents peak to peak ripple current.
) represents peak to peak ripple current.![]() ,
, ![]() ,
,![]() .
.
4. Predictive Current Control
Figure 4 shows the block diagram of the proposed predictive current control scheme. Predictive control is characterized by its system model usage that helps in predicting variables for future behaviour that necessitates controlling. Controller utilizes the particular information in order to choose the optimum switching state which in turn will be applied to the power converter, as per predefined optimization decisive factors.
4.1. Current Reference Generator
It is derived and designed so that the required current reference may be generated and the same may be utilized for compensating any undesirable load current components. With respect to this one, system voltages, DC link voltage of converter as well as the load currents are measured. During the unbalanced current/voltage conditions, PLL tuning is required. But, in order to improve the conventional PLL tuning, an intelligent ABC optimization algorithm is used in this approach
4.2. Predictive Model Using ABC
Converter model is employed for prediction of output current of the converter. Implying that considering a given sampling time ![]() , identifying converter switching states and control variables at instant
, identifying converter switching states and control variables at instant![]() , prediction of next states is feasible at any instant
, prediction of next states is feasible at any instant![]() . On account of first order nature that is inherent in state Equations (3-6) that entail details of the model, a relatively accurate first order approximation of the derivative has been taken in to consideration here as in Equation (9).
. On account of first order nature that is inherent in state Equations (3-6) that entail details of the model, a relatively accurate first order approximation of the derivative has been taken in to consideration here as in Equation (9).
![]() (9)
(9)
![]()
Figure 4. Proposed ABC based predictive current control scheme.
4.3. Proposed ABC Algorithms for Optimal Switching of the Converter
In [19] the authors proposed the Artificial Bee Colony algorithm wherein each of the colonies comprises of three groups the employed, the onlookers and the scouts. A random switching state ![]() is initialized and each solution vector is generated. Then, each employed bee found new sources whose quantity is equal to half of the total sources. The main purpose for determining the new food source is evaluation of nectar amount and subsequently greedy selection is carried out. In ABC, both employed and onlooker contribute as being part of the operation and scouts carry out exploration. Bees aim at maximizing food quantity brought back into the nest.
is initialized and each solution vector is generated. Then, each employed bee found new sources whose quantity is equal to half of the total sources. The main purpose for determining the new food source is evaluation of nectar amount and subsequently greedy selection is carried out. In ABC, both employed and onlooker contribute as being part of the operation and scouts carry out exploration. Bees aim at maximizing food quantity brought back into the nest.
Step 1: Generate the initial switching state![]() , where
, where ![]()
Step 2: Calculate the voltage for each switching state (particle) to obtain output voltage for each switching state V (Pi), and select the best ![]() as Pi.
as Pi.
Evaluate the fitness (output voltage for each switching state) (fi = Pi) of the switching state
Step 3: Use the iteration formulae of ABC to get a new routing path.
For each employed bee Do
Produce new solution ![]() of switching state of the inverter
of switching state of the inverter
Calculate the value ![]() of switching state of the inverter
of switching state of the inverter
Apply greedy selection process
Calculate the probability values Pi for the solutions ![]()
For each onlooker bee
Select a solution ![]() depending on Pi
depending on Pi
Produce new solution ![]()
Calculate the values ![]() Apply greedy selection process
Apply greedy selection process
If there is a discarded solution for the scout then replace it with a new solution which will be randomly produced.
Memorize the best solution so far.
The algorithm iterates to the preferred cycle number and the sources having the best nectar in mind gives the possible values of the variables. The obtained nectar amount denotes the solution of the objective function. The 8 possible output current predicted values can be obtained as in Equation (10)
![]() (10)
(10)
As shown in Equation (10), in order to predict the output current at the instant![]() , the input voltage value
, the input voltage value ![]() and the converter output voltage
and the converter output voltage ![]() are required. The algorithm calculates all 8 values associated with the possible combinations that the state variables can achieve.
are required. The algorithm calculates all 8 values associated with the possible combinations that the state variables can achieve.
4.4. Cost Function Optimization
Selection of optimal switching state applicable to power converter requires, comparison of 8 predicted values obtained for ![]() with reference by deploying a cost function g, as follows in Equation (11).
with reference by deploying a cost function g, as follows in Equation (11).
![]() (11)
(11)
Here ![]() represents the error difference between the actual filter currents
represents the error difference between the actual filter currents ![]() and the reference filter currents
and the reference filter currents ![]() . The output current
. The output current ![]() is equal to the reference current
is equal to the reference current ![]() when g = 0.
when g = 0.
Therefore, the main goal of the cost optimization is to achieve the g value close to zero. Voltage vector ![]() is selected as it reduces cost function and applicable for subsequent sampling state. Through each sampling state, switching state generating minimum value of g is chosen amongst 8 probable function values. Algorithm chooses that switching state which generates minimal value and then the same is applicable to the converter during the
is selected as it reduces cost function and applicable for subsequent sampling state. Through each sampling state, switching state generating minimum value of g is chosen amongst 8 probable function values. Algorithm chooses that switching state which generates minimal value and then the same is applicable to the converter during the ![]() state. An accurate and fast detection of the theta and frequency is essential to assure the correct generation of the reference signals. So, in this work, ABC optimization is used in PLL to optimize its parameters
state. An accurate and fast detection of the theta and frequency is essential to assure the correct generation of the reference signals. So, in this work, ABC optimization is used in PLL to optimize its parameters ![]() to obtain better steady state response, settling time, voltage magnitude and DC component elimination.
to obtain better steady state response, settling time, voltage magnitude and DC component elimination.
5. Current Reference Generation
DQ based reference current generation scheme has been employed here to attain active power filter current reference signals. The scheme offers quick and precise signal tracking capabilities. This particular feature negates voltage fluctuations deteriorating reference current signal that influence compensation performance [8] . Figure 5 shows how reference current signals are attained through matching load currents. This module calculates the necessary reference current signals for the converter so as to compensate reactive power, current harmonic & current imbalance respectively. The displacement power factor ![]() and the maximum Total Harmonic
and the maximum Total Harmonic
![]()
Figure 5. dq based reference current generator.
Distortion (THD) of the load ![]() defines the relationships between the apparent power needed by the active power filter, with related to the load, as shown in Equation (12)
defines the relationships between the apparent power needed by the active power filter, with related to the load, as shown in Equation (12)
![]() (12)
(12)
where the value of ![]() includes the maximum compensable harmonic current, defined as double the sampling frequency
includes the maximum compensable harmonic current, defined as double the sampling frequency ![]() . The frequency of the maximum current harmonic component to be compensated is equal to one half of the converter switching frequency.
. The frequency of the maximum current harmonic component to be compensated is equal to one half of the converter switching frequency.
DQ based scheme is operational as part of the rotating reference structure, hence measured currents need to be multiplied using ![]() and
and ![]() signals. Deployment of dq transformation, d current component synchronization needs to be done with respect to corresponding phase to neutral system voltage; q current component is phase shifted by 90˚. Obtaining
signals. Deployment of dq transformation, d current component synchronization needs to be done with respect to corresponding phase to neutral system voltage; q current component is phase shifted by 90˚. Obtaining ![]() and
and ![]() synchronized reference signals are done using SRF-PLL [20] . A pure sinusoidal waveform is generated by the SRF-PLL when there is severe distortion in system voltage.
synchronized reference signals are done using SRF-PLL [20] . A pure sinusoidal waveform is generated by the SRF-PLL when there is severe distortion in system voltage.
Eliminating of tracking errors is feasible as SRF-PLLs are designed so that phase voltage unbalancing is evaded, harmonics (i.e., less than 5% and 3% in fifth and seventh, respectively) and resultant offset generated on account of nonlinear load conditions and measurement errors.
Thus, for the complete removal of DC component and sudden response of frequency ABC is used in this work to tune the PLL block![]() . The settling time and the steady state response of the frequency are tuned by
. The settling time and the steady state response of the frequency are tuned by ![]() and
and ![]() gain values. Similarly, elimination of DC component and identifying the voltage magnitude are tuned through
gain values. Similarly, elimination of DC component and identifying the voltage magnitude are tuned through ![]() and
and ![]() gain values through the ABC optimization approach.
gain values through the ABC optimization approach.
Equation (13) shows the relationship between the real currents ![]() where
where ![]() and the associated dq components (
and the associated dq components ( ![]() and
and ![]() ) is
) is
![]() (13)
(13)
The DC component of the phase currents ![]() is extracted by a Low Pass Filter (LPF) to generate the harmonic reference components
is extracted by a Low Pass Filter (LPF) to generate the harmonic reference components ![]() . The corresponding Alternating Current (AC) and DC components of
. The corresponding Alternating Current (AC) and DC components of ![]() are phase shifted by 180˚ to obtain the reference components (reactive) of the phase currents. Maintaining DC voltage constant, the amplitude of the converter reference current should be modified by adding an active power reference signal
are phase shifted by 180˚ to obtain the reference components (reactive) of the phase currents. Maintaining DC voltage constant, the amplitude of the converter reference current should be modified by adding an active power reference signal ![]() with the d component discussed below. The resulting signals
with the d component discussed below. The resulting signals ![]() and
and ![]() are transformed as three phase signals by applying the inverse Park and Clark transformation, as shown in Equation (14). In this paper the cut off frequency of the LPF is used as 20 Hz.
are transformed as three phase signals by applying the inverse Park and Clark transformation, as shown in Equation (14). In this paper the cut off frequency of the LPF is used as 20 Hz.
![]() (14)
(14)
A significant advantages that dq based current reference generator scheme offers is that it facilitates a linear controller implementation in DC voltage control loop. Though, an obvious disadvantage that arises from dq based current reference frame algorithm, deployment for producing reference current generation is of second order harmonic components in ![]() and
and ![]() in an unbalanced operating state. Harmonics amplitude is based on the unbalanced load current percentage expressed as the relationship between the positive sequence current
in an unbalanced operating state. Harmonics amplitude is based on the unbalanced load current percentage expressed as the relationship between the positive sequence current ![]() and the negative sequence current
and the negative sequence current ![]() .
.
Traditionally PI controller is used to control the DC voltage of the converter. This is an important issue in the evaluation, since the cost function according to the Equation (9) is designed using only reference currents, in order to avoid the use of weighting factors. In general, these weighting factors are obtained experimentally, and they are not well defined for different operating conditions. In addition to that, the slow dynamic response of the voltage across the electrolytic capacitor will not affect the current transient response. For this reason, the PI controller represents a simple and successful way for the DC voltage control. The DC voltage remains constant (with a minimum value of ![]() until the active power absorbed by the converter decreases to a level of the inability to compensate it’s losses.
until the active power absorbed by the converter decreases to a level of the inability to compensate it’s losses.
The absorbed active power by the converter is controlled by adjusting the amplitude of the active power reference signal ![]() , which is in phase with each phase voltage. In the block diagram shown in Figure 6, the DC voltage
, which is in phase with each phase voltage. In the block diagram shown in Figure 6, the DC voltage ![]() is measured and then compared with a constant reference value
is measured and then compared with a constant reference value ![]() . The error (e) is processed by a PI controller, with two gains,
. The error (e) is processed by a PI controller, with two gains, ![]() and
and ![]() . Figure 6 shows that the output of the PI controller is given to the DC voltage transfer function
. Figure 6 shows that the output of the PI controller is given to the DC voltage transfer function ![]() , which is represented by a first order system are briefly explained in [21] .
, which is represented by a first order system are briefly explained in [21] .
In the conventional tuning of PLL there is a frequency jump in the grid voltage and a delay in theta tracking. Both will be varies with respect to the type of load used. Moreover the varying nature of RES produces ripples in the output which affects the grid voltage [22] [23] , which is given to PLL as feedback here. This will affect the injection time of the compensating current into the grid. To avoid these demerits in this paper the conventional method of tuning is replaced by ABC based tuning to enhance the performance of the overall system.
5.1. Modified Three-Phase PLL to Avoid DC Error
For a three phase balanced set of input signals is as shown in the Equation (15)
![]() (15)
(15)
and the d component is given as in the Equation (16)
![]() (16)
(16)
The loop regulates this quantity to zero and, thus, regulates φ to θ. Assume that the input signal has a DC component of ![]() ; then, a term as shown in Equation (17) will superimpose on
; then, a term as shown in Equation (17) will superimpose on ![]() . If the DC offset is unbalanced (i.e., has unequal values on three phases), this causes an error whose frequency is the same as
. If the DC offset is unbalanced (i.e., has unequal values on three phases), this causes an error whose frequency is the same as
![]() (17)
(17)
fundamental frequency. The proposed ABC based modified three phase PLL is shown in Figure 7. Here the block denoted by “dot” makes the dot product of its inputs: ![]() It is to be observed that the output of this block
It is to be observed that the output of this block
is equal to ![]() . Thus, the factor 2/3 is placed to make it equal to
. Thus, the factor 2/3 is placed to make it equal to ![]() .
.
5.2. Objective Function for Tuning PLL Using ABC Algorithm
This section discusses about the tuning of gain values to attain the optimal performance of PLL. ![]() value depends on the frequency factor ω ,
value depends on the frequency factor ω , ![]() gain value depends on the angle ∅ . The voltage magnitude is based on the
gain value depends on the angle ∅ . The voltage magnitude is based on the ![]() gain value where as the
gain value where as the ![]() gain value depends on the DC component. The objective function of this approach would be to minimize the THD and Settling Time ‘ST’ of the proposed model in Figure 8 as follows.
gain value depends on the DC component. The objective function of this approach would be to minimize the THD and Settling Time ‘ST’ of the proposed model in Figure 8 as follows.
![]()
Figure 6. DC voltage control block diagram.
![]()
Figure 7. ABC based modified three-phase PLL to avoid DC error.
![]()
Figure 8. Minimum cost function evaluation.
![]() (18)
(18)
where ![]() and
and ![]() are the parameters for calibration. The parameters subjected to limit, considered in this research work are
are the parameters for calibration. The parameters subjected to limit, considered in this research work are
![]() (19)
(19)
Manual tuning of the controller parameters in removing the performance becomes more difficult and consumes more time. To overcome this major drawback, ABC based optimization approach is proposed here to auto tune the controller parameters and also to improve the efficiency of the control strategy in extracting reference currents for SAPF under non linear load conditions also.
5.3. Working of the Proposed ABC based PI Self Tuning
1) Initialize the population (![]() ) of solutions
) of solutions
2) Initially, the controller parameter are generated which is of size N
3) Produce new solutions of DC components through employed bees and then apply greedy selection process
4) Probability values are calculated for the above solution
5) Produces new set of population for the parameters of the controller
6) Update the best values achieved so far, and sort the obtained values
7) Based on probability values again the new solutions are obtained through onlooker bees and then apply greedy selection process
8) Determine the left out solution for the scout, if exists, and replace it with a new randomly produced solution
9) Update the best value achieved so far
The proposed structure of Figure 7 the DC component in the input signal is detected by the branch comprises three integrators with equal gains ![]() to estimate the DC components on three phases. Since the DC components are estimated by this branch and added to the output, the signal e will have no DC. Thus the error in the whole loop is eliminated by removing the DC component, which assures the PLL operation no longer suffers from such components. The modified PLL equations are given in Equation (20).
to estimate the DC components on three phases. Since the DC components are estimated by this branch and added to the output, the signal e will have no DC. Thus the error in the whole loop is eliminated by removing the DC component, which assures the PLL operation no longer suffers from such components. The modified PLL equations are given in Equation (20).
![]() (20)
(20)
where ![]()
The variables V, ω and ![]() estimate voltage magnitude, frequency and angle of the input signal with nominal fundamental frequency of
estimate voltage magnitude, frequency and angle of the input signal with nominal fundamental frequency of ![]() . Thus it is observed that, besides THD and Settling Time of the DC link voltage
. Thus it is observed that, besides THD and Settling Time of the DC link voltage ![]() , the work also concentrates on choosing the optimal filter current with a minimum cost function.
, the work also concentrates on choosing the optimal filter current with a minimum cost function.
6. Simulation Results and Evaluation
This work has been simulated in MATLAB SIMULINK r2011a. This section clearly discusses about the performance evaluation of the proposed model in which the voltage source converter is controlled to achieve minimized current harmonics under non linear load conditions at unity power factor. Moreover, this proposed model is verified for the RES interconnection with inverter to attain balanced sinusoidal grid currents under unbalanced load conditions through ABC optimization technique. The other simulation scenario wherein the PLL is tuned to eliminate DC component, minimizing the peak overshoot and improving the settling time of frequency and theta is considered. In this simulation, the ![]() represents grid voltage,
represents grid voltage, ![]() represents grid current,
represents grid current, ![]() represents the load current,
represents the load current, ![]() represents the inverter current and
represents the inverter current and ![]() represents DC link voltage.
represents DC link voltage.
6.1. System Behavior with SAPF for Nonlinear Load under Balanced Condition
The nonlinear behavior of the three phase grid system with nonlinear balanced load condition and how the compensation is done with the help of the voltage source converter acting as SAPF for the grid connected PV system is clearly depicted in Figure 9. Figure 9(a) shows the grid voltage profile with the magnitude of 325 V, taken between line to ground for all the three phases. Here for the analysis a three phase diode bridge rectifier feeding resistive load is considered as nonlinear load throughout the simulation discussion. Due to this nonlinear load, the sinusoidal nature of the grid current is affected as shown in Figure 9(b) up to 0.22 seconds.
The nonlinear diode bridge rectifier will draw a nonlinear load current as shown in Figure 9(c). The effect of the SAPF on the grid current, load current and the DC link voltage is recognized from 0.22 seconds, since the converter starts to inject the compensating current, acting as SAPF from that moment as shown in Figure 9(d).
Now the compensating performance of the SAPF could be clearly understood from Figure 9(e) and Figure 9(f). For the clarity of understanding the current waveform is shown for phase “A” alone in Figure 9(e). The source current compensation could also be seen in Figure 9(b) after 0.22 seconds. The DC link grid voltage has rising nature up to 0.22 seconds and after the injection of compensating current, it is quickly forced to be maintained at 680 V as per the system design and the steady state nature could also be realized from Figure 9(f).
6.2. System Behavior with SAPF for Nonlinear Load under Unbalanced Condition
The performance of the ABC tuned SAPF for both nonlinear and unbalanced load conditions could be appreciated by analysing the waveforms shown in Figure 10.
Here the unbalanced condition is considered from 0.2 seconds onwards and up to that the system operates the nonlinear load under balanced condition only. Load unbalancing is created at 0.2 seconds, only on two phases i.e., phase A and phase B having 20A as unbalanced load currents. Phase C is kept in balanced nonlinear condition with the current magnitude of 14 A. This is shown in Figure 10(a). Figure 10(b) illustrates the compensating current generated by the SAPF which is to be injected into the grid for reducing harmonics and maintaining the balanced condition of the system.
Till 0.2 seconds the system has nonlinearity alone as shown in Figure 10(a). This nonlinear nature of the grid current for balanced condition is compensated by the proposed SAPF model to reduce the harmonic currents. After 0.2 seconds the SAPF is producing the compensating current to compensate the harmonic current as well as to make the system as balanced one.
The performance of the proposed model for the unbalanced nonlinear system is evaluated by investigating the waveform shown in Figure 10(c). Till 0.2 seconds the proposed model injects the compensating current waveform and thus making the grid current as sinusoidal one for the balanced system. The unbalanced system which is created at 0.2 seconds has become as a balanced linear system by drawing the current as 18 A in each phase approximately due to the optimal reference current generator.
6.3. Performance Evaluation of Proposed ABC Tuned and Conventional PLL
The main objective of this paper which is known as ABC tuned PLL with predictive current control method of SAPF is for optimizing the control parameters of the PLL can be evaluated by comparing it with the conventional PLL model, based on the factors frequency response, theta tracking, elimination of DC component and maintain the voltage magnitude of the system. Figure 11 shows the evidence for the better performance of the proposed PLL model compared to the conventional model.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 10. (a) Unbalanced nonlinear load current; (b) Inverter current for unbalanced load; (c). Grid current for unbalanced load.
Figure 11(a) compares the frequency response of the proposed model with the conventional model in tuning the PLL. It is clearly shown that the proposed model results in lesser peak overshoot and quicker settling time of the system frequency at 50 Hz. Moreover it holds good even under unbalanced load conditions. It could also be realized from the same figure at 0.2 seconds, at which the unbalancing is created in the system. Improving the frequency response is taken care by the proper tuning of the PLL parameter![]() .
.
Figure 11(b) compares the theta tracking response of the proposed model with the conventional model. It is clearly understood that the proposed ABC tuned PLL tracks the theta quickly even from 0.01 seconds where as it is higher for the conventional model of the PLL. The quicker theta tracking influences the generation of reference current, selecting the optimal switching of the converter and thus improving the harmonic compensation. By the proper tuning of ![]() gain value, good response in tracking the theta value could be done.
gain value, good response in tracking the theta value could be done.
Figure 11(c) shows the voltage DC component response of proposed ABC tuned PLL and the conventional SRF-PLL. The DC component may be naturally present in the input signal or may be generated due to nonlinear/unbalanced load conditions. This DC component creates low frequency oscillations that cannot be removed using conventional filtering techniques as it may degrade the overall performance of the system and thus an efficient PLL structure is essential. Now, in order to attain almost zero DC components, an efficient ABC optimization loop is integrated inside the PLL structure which results in effective elimination of the DC component by tuning the ![]() gain value. The optimal voltage magnitude response is attained by tuning the
gain value. The optimal voltage magnitude response is attained by tuning the ![]() gain value as shown in Figure 11(d).
gain value as shown in Figure 11(d).
With optimal tuning of ![]() gain value, lesser peak overshoot response is achieved in the proposed model and hence the quick settling and the improved magnitude response of the three phase system voltage with the fundamental frequency is as shown in Figure 11(e) in per unit value. Obtaining zero error in the comparison of
gain value, lesser peak overshoot response is achieved in the proposed model and hence the quick settling and the improved magnitude response of the three phase system voltage with the fundamental frequency is as shown in Figure 11(e) in per unit value. Obtaining zero error in the comparison of ![]() and
and ![]() as shown in Figure 11(f) increases the overall performance of the PLL and thus improving the performance of the proposed SAPF model for the interconnected PV system to the grid. The power factor of the grid system is nearest to unity as shown in Figure 11(g).
as shown in Figure 11(f) increases the overall performance of the PLL and thus improving the performance of the proposed SAPF model for the interconnected PV system to the grid. The power factor of the grid system is nearest to unity as shown in Figure 11(g).
6.4. THD Analysis of the System
Table 2 shows the harmonic analysis of the waveforms for the system without SAPF, with conventional SAPF and with the modified SAPF. It gives the THD value of the harmonic current of the system for the each case in balanced and unbalanced load conditions. It gives the THD comparison for the system under various harmonic orders.
7. Conclusion
The design of ABC based PLL tuned SAPF has been proposed in this paper for a grid connected solar PV system. The dynamic performance of the proposed model in compensating current harmonics and reactive power consumption is evaluated through the Matlab simulation. In this research, ABC optimization is proposed to select the optimal switching states that must be applied to the power converter, by selecting the best minimal optimal
![]()
Table 2. Analysis of % THD for the nonlinear load under balanced and unbalanced condition.
value “g”. Simulated results have proved that the proposed predictive control algorithm is a good choice to classical linear control methods and the compensation effectiveness of the proposed shunt active power filter with ABC based PLL tuning. The performance of the proposed approach has been evaluated under unbalanced load conditions and it is observed that the proposed modified PLL approach attains fast theta tracking as 0.15 seconds, quick settlement of frequency compared with ±0.2 Hz jumping of conventional model, maintaining of the DC voltage magnitude in 700 V within 0.4 seconds, zero error for the presence of DC component, improved settling time and minimal attainment of THD as 1.2% for balanced load and 3.79% for unbalanced load. In the future the work can be extended to improve the voltage quality of the system and the converter operation can be analyzed as a simple inverter for injecting the power derived from solar PV and as SAPF for current harmonic compensation. Instead of VSI, multilevel inverters may be used for harmonic reduction.