Hybrid Control Strategy for Matrix Converter Fed Wind Energy Conversion System ()
Received 20 April 2016; accepted 6 May 2016; published 18 August 2016

1. Introduction
Wind being one of the most clean and abundantly available sources of energy, significant effort is put to harness energy from wind. Since the available energy from the wind varies depending on a number of parameters such as environmental conditions, the amount of wind available, direction, and its speed; vigorous research is going on to extract this energy with minimal cost [1] [2] . Wind energy system consists of turbine, gearbox, generator and power conditioner. Various stages of harnessing this energy involve the conversion of kinetic energy to mechanical energy and then to electrical energy. The power conditioning circuit normally consists of power electronic converters.
Wind systems are mainly classified as constant/fixed speed systems and variable speed systems. The design of a fixed speed system is such that, it can provide maximum output power only at one speed. This limitation can be overcome by employing a variable speed system, in which the power can be extracted even if wind speed varies and hence the energy capture increases [3] [4] .
In wind energy conversion system, power electronics plays a vital role, in improving the quality of the electrical energy produced at the generator terminals [5] - [7] . Recently, many power electronics converters have been designed to get a constant output from the windmill, in which the two stage back-back converter is more popular, which consists of an inverter and a rectifier stage [8] [9] . The issues associated with these two stage converter are that, the conversion happens in two stages. Also, large DC link is required, whose designing is complicated. In these converters, large harmonics are produced due to the high frequency switching and hence large filters are essential to subdue them. Hence, it is essential to choose a converter which gives the finest performance [10] . The design and control method of the multifunctional capacitive coupling VSI is presented in [11] . Wind energy conversion system without a DC link including a boost converter is presented in [12] .
Matrix Converters (MC) are direct AC-AC converters that use bidirectional switches. In 1976, Gyugyi and Pelly introduced the concept of this converter [13] . The MC is capable of controlling the amplitude and the frequency of an input AC voltage. Venturini and Alesina termed the matrix converter as a generalized transformer [14] . Due to the simplicity of its construction, a single stage voltage and frequency conversion, high efficiency, reliability and absence of any DC link makes this converter a better choice over two-stage converters [15] . The control structure of a converter, which did not require DC link, was described by Zanchetta [16] . With a proper switching strategy the matrix converter can act as an inverter, rectifier, and frequency converter. The matrix converter can be labelled as a universal power converter as it offers multiple types of conversions [17] . The basic working principle and modelling of three-phase matrix converter is explained in literature [18] - [20] .
Applications of matrix converters include wind energy conversion system, speed control of motor, mobile utility power unit, induction heating and aircraft power supply.
In this work, hybrid control strategy for wind energy conversion system employing a matrix converter for the power conditioning is developed. An efficient modulation technique is developed to obtain desired output frequency and voltage. In order to extract maximum power from the wind turbine, a maximum power tracker is proposed. Also, an over current protection circuit is introduced to protect the converter from over current at the load circuit. Clamp circuit is provided between the input and output of the converter to remove DC component or spikes and protect the converter.
With the capricious wind speed, the output voltage, current and power from a wind generator may not be constant and it is still a challenge to get a constant output from the WECS. Wind energy is captured using a turbine and is converted to electric power using a generator. Currently, doubly fed induction generators and permanent magnet synchronous generators are more popular [21] - [24] . The main challenge in wind energy system is the storage of power in batteries due to the poor life time and long charging hours. Hence, grid connected system is preferred. A grid connected wind system is presented in [25]
The matrix converter can be employed as a powerful and efficient power converter in wind energy systems, to obtain a steady and constant output. Figure 1 shows the basic block diagram of a matrix converter fed wind energy conversion system.
![]()
Figure 1. (a) Block diagram of a matrix converter fed wind energy conversion system; (b) SVM Rectifier; (c) SVM Inverter.
At a particular velocity of wind, mechanical power obtainable from a wind turbine depends on shaft speed. If the turbine output power is large and sufficient, the generator is connected to the load through the power switch. But if mechanical power developed at the turbine is not sufficiently large, the generator will be disconnected from the load through the power switch. In that case, the generator will be connected through a matrix converter. Power tracker compares the actual speed of the rotor and the reference speed and an error signal is produced. This error signal is transmitted as feedback signal to the pulse generating and control unit of the matrix converter. The control unit calculates and produces switching pulses and applies to the matrix converter. MC adjusts the terminal frequency at the generator terminal, and thereby the speed of the turbine shaft. The matrix converter furthermore regulates the reactive power transfer at the load side transformer to voltage regulation and frequency.
Section 2 covers the modelling of wind turbine. Mathematical modelling of a matrix converter is dealt in section 3. The MATLAB simulation results of the MC suitable for WECS are presented in section 4. Details of the laboratory prototype and the hardware results are also dealt in section 4.
2. Modelling of Wind Turbine
In the wind energy conversion system, the conversion of wind energy is first transformed in to mechanical energy in the turbine, and then it is transformed in to electrical energy in the generator. But, the output electrical energy is purely based on the wind speed striking the blade of the turbine. Also, the steadiness of the output depends on the tip speed ratio (λ), pitch angle (β) and the wind speed (V) The available power from the wind can be expressed as,
 (1)
(1)
 (2)
(2)
where,
Pout is available wind power (Watt).
ρw is the moving air density (Kg/m3).
AS is the Swept area by the blade (m2).
V is the wind velocity (m/s).
C is the power coefficient, which depend on the tip speed ratio and pitch angle.
The torque developed in the turbine can be stated as,
 (3)
(3)
where,
Tw = Torque developed.
ωrotor = Rotor speed (rad/sec).
The power coefficient is given by,
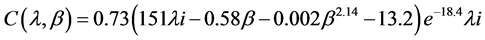 (4)
(4)
where,
 (5)
(5)
λ is given by,
 (6)
(6)
Variation of lambda with power coefficient and power with wind speed are plotted using MATLAB and are as shown in Figure 2 and Figure 3.
![]()
Figure 2. Coefficient of power with tip speed ratio.
![]()
Figure 3. Output power from turbine with wind speed.
3. Modelling of Matrix Converter
Figure 4 displays a 3 × 3 Matrix Converter (MC), which comprises of 9 bidirectional switches. These switches are connected in such a manner that, any of the three inputs can be connected to any of the three output phases. With these switches, MC can have 29 switching states, provided no short circuiting in the input and no open circuit at the output.
Matrix converter is analogous to the combination of an inverter and a rectifier with a virtual DC link as shown in the Figure 1. Switches S1-S6 serves for the rectification stage(R) and the switches S7-S12 serves for the inversion stage (I). Vector modulation control for these two stages is developed and then, combined vector modulation is applied to the matrix converter for obtaining the preferred output.
Hence, Transfer function (TF) of MC can be given as,
 (7)
(7)
For the vector modulation scheme, the space transformation method is used. In space transformation method, any function of the form Va(t) + Vb(t) + Vc(t) = 0, can be transformed to 2-dimensional space coordinates. The co-ordinate transformation from the a-b-c axis of voltage vectors to α-β axis is given by,
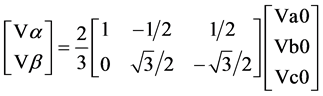 (8)
(8)
Only eight acceptable combinations of switching are possible in the operation of inverter without having any short circuit. At a time at least three switches conduct. The output equation of the inverter can be written as,
 (9)
(9)
In the vector modulation scheme, eight switching combinations form 6 active vectors (non-zero output voltage) and 2 zero vector (zero output voltage). Space vectors representing output voltage and current can be written as,
 (10)
(10)
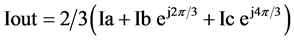 (11)
(11)
In the rectifier stage, at a time two switches conduct simultaneously (one from the upper leg and one from the
![]()
Figure 4. Schematic diagram of a 3 × 3 matrix converter.
lower leg). There are four switching states for the rectifier. Switch state “+1” indicates that the top switch in the converter leg “A” is switched ON and the lower is OFF. The switch state “−1” indicates that the top switch is OFF and the lower switch is ON. Switching state “0” indicates both the devices in the same leg are OFF and the switching state “2” indicates that both the switches in the same leg are turned ON. During the switching state “1”, the converter current is equal to Id, during the state “−1” converter current is equal to ?Id, and during the switching state “0” and “2” the converter current will be zero. For conduction of current through the rectifier, two switches must be conducting at any given time. For the space vector modulation for rectifier, we need to consider nine switching states, in which 6 are active states and 3 are zero states. Vector modulation switching states of the inverter and the rectifier is given in the Table 1.
Current modulation is used in the rectifier stage. Let us consider the rectifier with three-phase balanced system. The input current of the rectifier can be written as,
![]() (12)
(12)
where irA, irB, and irC are the rectifier input currents.
These three-phase current in the a-b-c frame can be transformed to two phase α-β frame using the equation,
![]() (13)
(13)
Space vector equation of three-phase current can be written in terms of two-phase current as,
![]() (14)
(14)
Combining Equations ((13) and (14)), we get,
![]() (15)
(15)
In a complex plane, these space vectors can be shaped as a regular hexagon. The space vector diagram for the inverter and rectifier stages is shown in Figure 5.
The required reference output voltage “Vref” of the inverter is obtained using two adjacent vectors Vα, Vβ, and zero vectors V7 and V8. Assuming t1, t2, t7 and t8 are the dwell time durations along these four vectors, the sampling time of inverter, Tsi, can be written as,
![]() (16)
(16)
Resulting space vector can be expressed as sum of vectors (t1/Tsi)*Vα and (t1/Tsi)*Vβ
Ampere second balancing equations are used for calculating dwell times for vector modulation of rectifier. The reference current vector can be synthesized with the two adjacent current vectors (two active vectors and zero vectors) i.e. in the first sector, reference current iref is synthesized using the three vectors I1, I2 and I0. Consider the dwell time duration for these three current vectors are T1 + T2 + T0. The sampling period of rectifier can be written as,
![]()
Table 1. Switching states of rectifier and inverter stage.
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
where mi is the modulation index and is given by,
![]() (21)
(21)
Output voltage of the MC is given by,
![]() (22)
(22)
The transfer function of the matrix converter is obtained as,
![]() (23)
(23)
Substituting the Equation (23) in Equation (22) through Equation (7), we get
![]() (24)
(24)
From the Equation (24), the matrix converter can be formed as shown in Figure 6.
4. Results and Discussions
4.1. Simulation Results
Modelling of the matrix converter system and the simulation has been carried out using MATLAB. Since the frequency of the generator output varies with wind speed, simulation is performed to obtain a constant frequency output voltage from a variable frequency input.
MATLAB simulation circuit of a matrix converter fed wind energy conversion system is shown in Figure 7. It consists of wind turbine block, generator block, matrix converter block, pulse generating circuit, and load circuit. Output of the wind turbine is applied to permanent magnet asynchronous generator. The generator converts the mechanical energy into electrical energy if the wind speed is in the range of 5 m/s to 15 m/s. Since the output voltage and frequency of the generator output varies with wind speed, to obtain a constant output voltage and frequency, a matrix converter is employed. Depending on the output requirement, the switching circuit generates the pulses to be applied to the switches. Vector modulation technique is used for generating the switching pattern.
Figure 8 explains selection of switches of the matrix converter using combined vector modulation of the inverter and the rectifier stage.
![]()
Figure 6. Equivalent diagram of matrix converter.
![]()
Figure 7. Simulation circuit of the matrix converter.
![]()
Figure 8. Selection of switches for the matrix converter.
![]()
Table 2. Output voltage and current with harmonic distortion values.
Mechanical energy is proportional to the wind speed. Wind speed is considered to be varying between 5 m/s to 15 m/s. The rotor turns at sub-synchronous speed, when the speed of the wind is lesser than 10 m/s, and above which it is at hyper-synchronous speed. When the wind speed is less than 5 m/s or above 15 m/s, the generator will be shut down and there won’t be any output across the load.
The output voltage and current along with the harmonic distortion values of voltage and current at 50 Hz are tabulated in Table 2.
The output voltage and current waveform for an output frequency of 50 Hz are shown in Figure 9. Also the harmonic spectrum of the phase current and voltage for the corresponding frequencies are also shown.
Various modulation strategies for a matrix converter has been studied and simulated. It has been noted that the vector modulation scheme gives the best performance with respect to Venturini’s method and modified Venturini’s method. A comparison of various modulation strategies are tabulated in the Table 3(a) and Table 3(b).
A comparison of various modulation strategies are illustrated in Figure 10. It has been found that the rms voltage and current for a particular value of modulation index is better with vector modulation technique, compared to direct modulation method (Venturini method) and modified Venturini method. Also, the voltage and current harmonics profile is improved in the vector modulation technique.
The phase voltage and phase current along with the harmonic spectrum at 50 Hz for various modulation strategies has been given in the Table 4. It has been noted that the vector modulation scheme gives the maximum phase voltage and current. Also, total harmonic distortion is reduced compared to other technique.
4.2. Experimental Evaluation
Laboratory prototype of the proposed matrix converter suitable for wind energy conversion systems to drive an induction motor has been built and is shown in Figure 11. The prototype is tested to obtain the desired performance. An rms voltage of 75 V is applied through an input filter, which is connected between the input and the converter. Figure 12 shows the hardware block diagram.
The power circuit consists of 6 IGBT’s per phase, which makes a total number of 18 switches for the func-
![]()
Figure 9. (a) Output voltage at 50 Hz. (b) Output current at 50Hz. (c) Voltage spectrum at 50 Hz. (b) Current spectrum at 50 Hz.
(a) ![]() (b)
(b) ![]()
Table 3. (a) Output voltage at 50 Hz with harmonic values―comparison of modulation strategies; (b) Output Current at 50 Hz with harmonic values― comparison of modulation strategies.
![]()
Figure 10. A Comparison of modulation strategies. (a) rms output voltage at 50 Hz. (b) rms output current at 50 Hz. (c) Harmonic spectrum of output voltage. (d) Harmonic spectrum of output current.
![]()
Table 4. A comparison of the various modulation techniques.
tioning of the converter along with PWM isolators and driver circuit. The converter is designed for an input of three phases, 0 - 100 V, 5A AC. An FPGA controller, which can be used to generate SPWM signals for the 9 switches of the MC, depends on the output requirement, is used for the real time control of the converter. Xilinx Spartan 3, XC3S400PQ208 with an on board 8 MHz crystal has been used for the hardware implementation. The PWM frequency is 10 kHz.
An input filter with inductor value of 3 mH/6.7A and capacitor value of 3 µF has been used in the input filter. A diode clamp circuit protection and an over current protection is introduced, for the common protection of the converter. Surges might be produced either in the input or output of the converter or due to the sudden shut down of the Matrix converter. Diode clamp protection circuit reduces spikes or surges and protects the converter switches. An over current protection circuit is designed to protect the system from over currents due to the imbalance in load circuit. If there are any discrepancies, the over current protection circuit protects the system, by automatically disabling the pulses, and hence switching off the converter. Hall Effect sensors are used for the measurement of current in the input and output of converter.
The control algorithm allows the converter to operate at a fixed frequency of 50 Hz, even if there is change in frequency in the input. The converter is designed to obtain an output frequency range of 10 - 60 Hz. The spectral analysis is also done and compared with earlier modulation techniques. The hardware output parameters match with the simulation results. Hardware Specifications are given below.
Power circuit input: Three-phase 0 - 100 V AC,
Output: Three phase output,
Power device: IGBT-CT60AM,
Maximum number of PWM inputs: 18,
Maximum PWM voltage: 5 V,
Switching frequency: 10 KHz,
Filter Inductor: 3 mH/6.7A,
Filter capacitor: 3 µF.
The hardware results in Figure 13 show that the Matrix converter is capable of operating at variable frequency, and is suitable for wind energy conversion systems. Switching pulses are generated and applied to the switches of the MC so that the required output frequency is obtained.
5. Conclusions
In this paper, a hybrid control strategy for a matrix converter fed wind energy conversion system is presented. Various modulation techniques for the control of the matrix converter have been simulated, and a refined control structure, using a vector modulation scheme, has been developed. From the simulation results it has been noted that the voltage transfer ratio is improved compared to the older control methods. Also the current and voltage harmonics are reduced in the proposed system. A control strategy to control the wind power at the input is also proposed. A power tracker is included in the system to extract maximum power from wind.
The developed hybrid control strategy produces better performance indices than other schemes. The system is simulated using MATLAB simulation software and a laboratory prototype is developed using an FPGA controller. An over current and clamp circuit protection is introduced in the hardware circuit. It protects the system from the over current and also reduces the spikes generated at the output of the converter. The hardware results are found to be matching with the simulation results.
In this proposed method, the maximum voltage transfer ratio is limited to 86% due to the switching losses. In the future, a cascaded matrix converter can be designed and included to improve the voltage transfer ratio and thereby obtain maximum output power.
Acknowledgements
This research work is funded by All India Council for Technical Education (AICTE), India. We would like to thank AICTE for the financial support provided for the research work.