Labor-Leisure Choice: Is Everything as Straightforward as One Might Have Thought? ()
Received 3 July 2016; accepted 8 August 2016; published 11 August 2016

1. Introduction
The benchmark neoclassical life-cycle model of labor supply and consumption/saving was developed by [1] , and later revisited by [2] . Yet the authors and many subsequent studies focused only on an interior solution for the optimal labor/leisure choice. In this paper, we focus on some fundamental issues that have been overlooked when focusing on such solutions.
First, in reality the time constraint on leisure does bind (i.e., individuals do quit the labor force). Thus the model is yet to answer what rational labor supply behavior should be in theory when the constraint is active, which is likely to become relevant once a full spectrum of the model’s parameters is considered. It might be that what contemporary studies find confusing in labor market behavior is actually perfectly natural, and hence various criticisms of intertemporal labor supply frameworks might have been overstated.1 Second, quantitative- theoretical models typically consider parameterization under which a representative agent in a frictionless environment always works non-stop right after he enters the model, before permanently retiring at a reasonably senior age. For the sake of convenience, we call that type of behavior “standard”. Yet so far, to our knowledge, neither [1] nor closely-related studies have systematically analyzed such a standard behavior via conventional mathematical techniques. We believe that this was done to simplify the mathematics involved. Indeed, researchers who work closely on optimal control problems know that inequality constraints in even relatively simple settings make the analytical solution to these problems very difficult, sometimes even impossible, to obtain (see, e.g., [6] ). However, we wondered whether simplifying the solutions of the model threw the baby out with the bathwater.
Hence, it is also unclear how easy it is to obtain the standard behavior in a typical labor-leisure choice frame- work. In addition and importantly, it is not at all clear whether very “non-standard” labor supply patterns can arise even in a totally frictionless economic setting when the time constraint on leisure binds, urging, for instance, the agent to quit and re-enter the labor force multiple times.
In this study, we use optimal control theory to explicitly provide a complete analytic solution to the benchmark model, which gives rise to the standard labor supply behavior. We use the benchmark model à la [1] and [2] as the foundation of our analysis because the model straightforwardly and elegantly describes the intertemporal choice in a high-frequency setting. The model is also convenient to use because it can be naturally framed within continuous time optimal control theory. The latter is a well-developed, carefully researched, and leading branch of mathematics,2 so we rely on it during our solution exercise.
Upon solving the model, we find that the standard labor supply behavior holds for a very limited range of the model parameters. For other parameters, we observe that either the agent never retires (time endowment constraint never binds), or retires unrealistically late in life. One can certainly think of various extensions of the model and additional assumptions (e.g., rapidly declining health status with age) that might cause the agent to retire much earlier in life. However, to what extent such assumptions are both helpful and realistic is a question future research should shed some light on.
Even more alarming, we find that under many sensible parameters, the labor supply behavior is not standard and cannot be straightforwardly determined from the analytic standpoint. We thus proceed by applying numerical software to the model. Doing so confirms our analytic suspicion that for those alternative parameters, the labor supply choice gets very confusing, and very hard to interpret intuitively a priori. For example, despite the absence of any friction or behavioral defects, rational agents often decide to frequently enter/exit the labor market, while frequently displaying prolonged voluntary absenteeism from work (sometimes spanning for a few decades), thus being completely at odds with intuition. In fact, non-standard labor supply behavior often arises for our model’s preference parameters identified as realistic in various micro studies. There is an enormous amount of literature on consumption smoothing and related topics, and perhaps it is time to investigate how smooth and predictable labor supply behavior can be.
We would like to emphasize that not knowing the root causes of remaining out of a job may bias policy analysis. Let us consider maternity-related career breaks as an example. Can we argue that historically, many females have exited the labor force because of a genuine maternal reason or because having a child is a legitimate and financially more attractive option to retain the job and the benefits while being away from work, with the latter being the main driving force? For the sake of an argument, let us suppose that childbearing motives are rather weak to start with and that a person is not really inclined to interrupt her employment at a young age. In this example, many typical proposals encouraging maternity leave would be inefficient. Alternatively, can we say that many people who remain unemployed for years are as such primarily because of existing structural problems in the economy (e.g., poor public education that makes young people unproductive, artificial scarcity created by non-competitive economic sectors) or primarily because such a behavior naturally follows from people’s intertemporal optimization exercise? Thus, a complete understanding of a rational, intertemporal labor supply choice even in a seemingly straightforward, totally friction-free environment requires further in-depth analysis.
We would like to acknowledge that, based on Heckman’s benchmark model, most contemporary quantitative-theoretical studies introduce sophisticated and realistic assumptions. Such models are plentiful in the areas of real-business-cycle fluctuations, public pensions, and so on. However, our point in this study is not to argue against the augmentation of Heckman’s framework (or to downgrade the importance of new assumptions and features found in the more recent literature) but to show that very puzzling and unexpected labor supply patterns are likely to arise even in a model that is totally straightforward and friction-free. We thus have plausible reasons to suspect that many existing labor/leisure models in quantitative-theoretical studies, however sophisticated, have yet to answer the same questions that confront the stylized benchmark model à la [1] [2] when a full spectrum of parameters is considered in those studies. In other words, predicting how the labor supply of various individuals will react to policy changes and modeling assumptions may not be as straightforward and easy as one might have assumed. We thus hope to stimulate future research to deeply investigate intertemporal labor supply behavior.
In what follows, Section 2 provides brief literature review. Section 3 presents a basic traditional model, while Sections 3.1 and 3.2 present analytic solutions. Section 4 presents numerical results based on the analytic derivations, while Section 5 briefly summarizes the results generated by the numerical software. The last section presents the conclusion.
2. Literature Review
Many other studies apply a variant of the benchmark life-cycle labor/leisure choice model to examine a wide range of policy-relevant questions. To our knowledge, however, none of these studies identify a nonstandard labor supply path as a potential issue. For instance, [18] models a standard labor supply structure and investigates different labor types in production and how their elasticity of substitution affects the outcome of social security and tax reforms. The study of [19] analyzes the macroeconomic and welfare effects of ending mandatory retirement within a life-cycle environment where lifetime is divided between working and retirement periods. In general, studies that use a similar labor supply structure in analyzing important issues, such as pension reforms, taxation, aging, and fertility, or studies that assume a clear career interruption channel are not scant (see, e.g., [20] - [22] ).
3. Model: Basic Setup
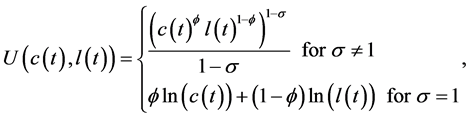 (1)
(1)
where 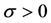 is the parameter of the inverse elasticity of intertemporal substitution, and
is the parameter of the inverse elasticity of intertemporal substitution, and 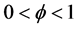 captures the trade-off between leisure and consumption. Time endowment is normalized to unity.
captures the trade-off between leisure and consumption. Time endowment is normalized to unity.
3.1. Our Solution: The Constrained Control Problem
Let the rate of time preference be denoted by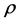 . The agent’s problem is to
. The agent’s problem is to
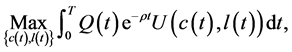 (2)
(2)
subject to the budget equation, control region, and the end-point conditions, given in (3)-(6):
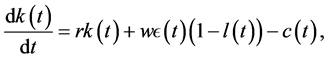 (3)
(3)
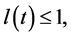 (4)
(4)
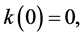 (5)
(5)
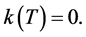 (6)
(6)
Remark 1. [1] , [2] and closely-related studies ignored constraint (4).
We thus define the Hamiltonian function
![]() (7)
(7)
where ![]() is a time-varying multiplier.
is a time-varying multiplier.
Optimal controls must be chosen so the following conditions are satisfied:3
![]() (8)
(8)
![]() (9)
(9)
and
![]() (10)
(10)
A necessary condition is that there exists a time-dependent multiplier![]() , so that if the Lagrangian of the Hamiltonian
, so that if the Lagrangian of the Hamiltonian
![]() (11)
(11)
then the following conditions are satisfied:
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Let us make a hypothesis that the structure of the solution is consistent with the standard behavior. Let there be some internal point in time (switching time) ![]() (to be determined) on and after which the agent completely stops working, and hence optimal leisure is
(to be determined) on and after which the agent completely stops working, and hence optimal leisure is![]() . Thus,
. Thus,
![]() (16)
(16)
![]() (17)
(17)
A complementarity condition implies that if![]() , then
, then![]() , and we have the system of equations
, and we have the system of equations
![]() (18)
(18)
Similarly, if![]() , then
, then![]() , and we have the system of differential equations
, and we have the system of differential equations
![]() (19)
(19)
Hence, the solution to the problem can be found by piecing together the solution of (18) and (19). In doing so, we first note the multiplier function ![]() is defined over the entire region
is defined over the entire region![]() , and from (18) and (19) it clearly obeys the same law of motion on each subarc. Since the function is required to be continuous, we get
, and from (18) and (19) it clearly obeys the same law of motion on each subarc. Since the function is required to be continuous, we get
![]() (20)
(20)
where a is a constant to be determined.
From (12) we deduce that
![]() (21)
(21)
Now, note that if![]() , then
, then![]() , meaning that (21), being substituted into (13), would result in
, meaning that (21), being substituted into (13), would result in
![]() (22)
(22)
Recall that![]() . Using this in (22), we can express the constant a in terms of
. Using this in (22), we can express the constant a in terms of ![]() as follows
as follows
![]() (23)
(23)
Thus,
![]() (24)
(24)
Substituting (24) into (21) and recalling that ![]() if
if![]() , we deduce from (19) that
, we deduce from (19) that
![]() (25)
(25)
for![]() .
.
Using the boundary condition (6), we find the solution to (25) as
![]() (26)
(26)
for![]() .
.
Evaluating (26) at![]() , we obtain
, we obtain
![]() (27)
(27)
Next, substituting (24) into (12) and (13) and considering the ![]() case, we solve for the time-dependent consumption and leisure paths as functions of
case, we solve for the time-dependent consumption and leisure paths as functions of ![]() as follows
as follows
![]() (28)
(28)
![]() (29)
(29)
for![]() . Here
. Here
![]() (30)
(30)
![]() (31)
(31)
Substituting (28) and (29) into (18), we obtain
![]() (32)
(32)
for![]() .
.
Using (5), we solve (32) as
![]() (33)
(33)
for![]() .
.
Because of the required continuity of![]() , we obtain from (33)
, we obtain from (33)
![]() (34)
(34)
Hence, ![]() is the solution to the following equation
is the solution to the following equation
![]() (35)
(35)
Let “RHS” stand for “the right-hand-side” expression. We then summarize the solution to problem (2)-(6) for this section as
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
where ![]() solves (35), the costate variable is determined from (24), and
solves (35), the costate variable is determined from (24), and ![]() is found from (13).
is found from (13).
3.2. A Typical, Heckman/Bütler-Type Solution: An Unconstrained Control Problem
Let us consider the Heckman/Bütler-type solution where the constraint on leisure is inactive. This would lead to the following optimal solutions for the consumption, leisure, and capital account paths, given respectively by (39)-(41).
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
for![]() , where the subscript “un” stands for “unconstrained” optimization,
, where the subscript “un” stands for “unconstrained” optimization, ![]() ,
, ![]() are defined earlier, and4
are defined earlier, and4
![]() (42)
(42)
4. Numerical Results Based on Analytic Derivations
We assume the maximum life length is 100 years as mortality data based on the U.S. life tables were top cut at age 100 [23] . We set our survival probability ![]() to [23] ’s sextic polynomial, and set efficiency profile
to [23] ’s sextic polynomial, and set efficiency profile ![]() to the author’s quartic polynomial, yet forcing the latter to keep steadily decaying (since [23] ’s polynomial picks up in old ages). As we model agents from age 25 onward, we set
to the author’s quartic polynomial, yet forcing the latter to keep steadily decaying (since [23] ’s polynomial picks up in old ages). As we model agents from age 25 onward, we set![]() . Various quantitative-theoretical life-cycle studies (e.g., [24] - [26] ), replicating some key steady-state targets in the U.S. economy, often compute the equilibrium wage rate to be in the vicinity of 1, so we set
. Various quantitative-theoretical life-cycle studies (e.g., [24] - [26] ), replicating some key steady-state targets in the U.S. economy, often compute the equilibrium wage rate to be in the vicinity of 1, so we set![]() . We set
. We set![]() , which is a reasonable rate for a yearly risk-free return. Since calibrated macroeconomic models justify the discount rate of about 3% per annum, or sometimes even slightly negative (see, e.g., [20] ; [23] ; [24] ), we vary
, which is a reasonable rate for a yearly risk-free return. Since calibrated macroeconomic models justify the discount rate of about 3% per annum, or sometimes even slightly negative (see, e.g., [20] ; [23] ; [24] ), we vary ![]() from 1 to percent per annum. The literature typically considers a much wider range for the elasticity parameter
from 1 to percent per annum. The literature typically considers a much wider range for the elasticity parameter ![]() (see, e.g., [27] ; [28] ) so we vary that parameter from 0.5 to 10.
(see, e.g., [27] ; [28] ) so we vary that parameter from 0.5 to 10.
Our numerical experiments are presented in Tables 1-3. The numerical entries (retirement ages under standard behavior) in the tables are rounded up to the nearest integer for the ease of illustration. “nb” means the time constraint never binds, i.e., the agent never retires. “?” means the labor supply behavior is yet to be determined and is likely to feature multiple switching points, and/or some pronounced absenteeism from the job market.
Remark 2. Many parameters result in the agent working non-stop all his life (solutions (39)-(41) i.e., “nb”). For other parameters, the agent manages to retire but extremely late in life. And only a couple of realistic retirement
![]()
Table 1. Labor supply choice (ρ = 1%).
![]()
Table 2. Labor supply choice (ρ = 2%).
![]()
Table 3. Labor supply choice (ρ= 3%).
ages are seen from Table 1 (for ![]() being in the vicinity of 3 to 4, and for low
being in the vicinity of 3 to 4, and for low ![]() values). Importantly, unknown labor supply behavior arises for the preference parameters often identified as realistic (see entries with ?s).
values). Importantly, unknown labor supply behavior arises for the preference parameters often identified as realistic (see entries with ?s).
Recall various retirement confidence surveys of American households reveal the majority of the population often prefer to retire around 65 - 70 years of age, and we see that very few parameters lead to such incentive. What is more troubling is that it is not clear what the labor supply would be when ![]() is in the vicinity of 1, and when
is in the vicinity of 1, and when ![]() is in the vicinity of 0.3 (Table 1). Based on the large body of evidence from the micro studies, [29] claims that
is in the vicinity of 0.3 (Table 1). Based on the large body of evidence from the micro studies, [29] claims that ![]() is close to unity. Macroeconomic studies often assume a very low degree of impatience, therefore it is not unreasonable to assume that an average discount rate might be close to 1% as in Table 1.
is close to unity. Macroeconomic studies often assume a very low degree of impatience, therefore it is not unreasonable to assume that an average discount rate might be close to 1% as in Table 1.
5. Numerical Results Based on an Optimization Software
We have shown that optimal intertemporal labor supply behavior is yet to be determined for a non-trivial number of conventional parameters. We tried to make our conclusions via explicit, mathematical derivations, but one can easily see that even for the basic, totally friction-free model, it is too challenging to generate all the possible solutions via a “pen-and-a-paper” method. Thus, in this section, we resort to a numerical optimization software to shed further light on the optimal decisions of the agent under the full spectrum of the model’s parameters.
In particular, we use the GPOPS-II (a MATLAB) software package developed for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming as described in [30] . We do not intend to bore the reader with the technicalities behind the software as the authors themselves have described them excellently and in detail.
For the sake of brevity, we do not show here the computational codes or all the results we have generated (though they are readily available upon request). Instead, we briefly summarize the generated results in the following remark.
Remark 4. First, GPOPS-II software confirms all our results presented in Tables 1-3. Second, for those parameters where analytically it was not possible to show the pattern of the labor supply behavior (see ?s in the above tables), we obtained the following results: The labor supply path either displays a few entries and exits to the labor market, or shows prolonged absenteeism from work (sometimes spanning decades) for no apparent reason. In most cases, the corresponding consumption path remains “deceivingly” quite smooth. It is extremely difficult to intuitively link the full spectrum of highly unusual labor supply patterns given the values of corresponding model parameters.
6. Conclusions
We revisit a seminal life-cycle rational model of intertemporal labor/leisure, consumption/saving choice. To our knowledge, previous studies have not systematically analyzed labor supply behavior via conventional mathematical techniques, and considered rather narrow space of preference parameters in simulation exercises. We believe that this was done to simplify the mathematics and computations involved, yet we show aforementioned simplification might leave us with many questions to answer.
We find that the above friction-free model either fits the real facts very poorly, or results in a very non- conventional labor supply choice over time which is very hard to predict a priori or intuitively interpret. Yet optimal consumptions paths nearly always remain quite smooth, almost deceiving the researcher that there should not be any “anomaly” in the labor supply path. Despite the absence of any friction or behavioral defects, rational agents often decide to frequently enter/exit the labor market, while frequently displaying prolonged voluntary absenteeism from work (sometimes spanning for a few decades), thus being completely at odds with intuition. In fact, non-standard labor supply behavior often arises for our model’s preference parameters identified as realistic in various micro studies. There is an enormous amount of literature on consumption smoothing and related topics, and perhaps it is time to investigate how smooth and predictable labor supply behavior can be.
Thus, as a simple rational choice model delivers surprising labor supply decisions, we wonder whether we fully understood rational labor choice behavior to begin with, and whether more sophisticated models would be immune to the above problems once a researcher considers a full spectrum of the model parameters. Apparently, confusing labor supply patterns are a natural feature of the mathematical solution to a completely standard, intertemporal neoclassical consumption-saving/labour-leisure model that is often used in one form or another, as a foundational block behind many applied studies. A complete intuitive understanding of a rational, intertemporal labor supply choice even in a totally friction-free environment requires further analysis.
Acknowledgements
We are grateful to Frank Caliendo, James Feigenbaum, and the seminar participants at Deakin University and American University of Sharjah for many helpful comments and suggestions. Special thanks go to the editor and two anonymous referees, whose thoughtful suggestions have considerably strengthened the paper. All errors are our own.
NOTES
![]()
1Some of the so-called paradoxes identified in the literature include the tendency of many workers to stop working until an overtime premium begins [3] , the tendency of taxi drivers not to work more hours when customers are plentiful [4] , a negative effect of a decrease in wealthy husbands’ incomes on some women’s labor force participation [5] , etc.
2Further to this, ( [7] , p. 65]) and ( [8] , p. 411]) provide examples of the importance of continuous time models in various economic applications involving intertemporal consumption/savings choice.
![]()
3A reader may refer, for instance, to [6] , or any standard book on deterministic optimal control.
![]()
4The proof of these results is quite tedious, yet straightforward, and thus we omit them here for the sake of brevity. They can be found in a technical appendix available upon request.