Chaos Anti-Synchronization between Chen System and Genesio System ()

Subject Areas: Chaotic System, Anti-Synchronization, Adaptive Control

1. Introduction
Since the pioneering work by Pecora and Carroll [1] , chaos synchronization, a very active topic in nonlinear science, has received increasing attention. The concept of synchronization has been extended in scope, for example to generalized synchronization [2] - [4] , phase synchronization [5] , lag synchronization [6] , and even anti-phase synchronization (APS) [7] - [9] . APS can also be interpreted as anti-synchronization (AS), which is a phenomenon in which the state variables of the synchronized systems have the same amplitude as but opposite signs to those of the driving system. Therefore, the sums of two signals are expected to converge to zero when AS appears. Recently, Singh and Roy generalized active control to AS for two systems [10] . However, it seems that there are fewer previous results on AS between two different systems with unknown parameters using adaptive control. In this paper, we will focus on the AS of two different systems. Adaptive control methods will be employed; a sufficient condition for anti-synchronization is derived rigorously. Numerical simulations on Chen system and Genesio system are performed, which demonstrate the effectiveness and feasibility of the proposed control technique.
The layout of the rest of the paper is as follows. Section 2 describes the systems and their mathematical models; in Section 3, adaptive anti-synchronization between Chen and Genesio systems is presented; numerical simulation results are given for illustration and verification. Finally, conclusions are drawn in Section 4.
2. Systems Description and Mathematical Models
Consider nonlinear chaotic system as follows.
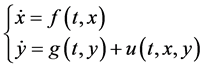 (1)
(1)
where 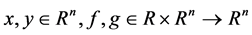 are differentiable functions, the first equation in (1) is the drive system, and the second one is the response system,
are differentiable functions, the first equation in (1) is the drive system, and the second one is the response system, 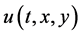 is the control input. Let
is the control input. Let 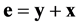 be the anti-synchro- nization error, our goal is to design controllers
be the anti-synchro- nization error, our goal is to design controllers  such that the trajectory of the response system with initial conditions
such that the trajectory of the response system with initial conditions 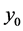 can asymptotically approach the drive system with initial conditions
can asymptotically approach the drive system with initial conditions  reversely and implement anti-synchronization finally, in the sense that
reversely and implement anti-synchronization finally, in the sense that
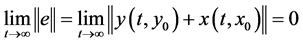
where  is the Euclidean norm.
is the Euclidean norm.
The Genesio system, proposed by Genesio and Tesi [11] , is one of paradigms of chaos since it captures many features of chaotic systems. It includes a simple square part and three simple ordinary differential equations that depend on three negative real parameters. The dynamic equations of the system is given by
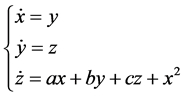 (2)
(2)
where 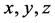 are state variables, when
are state variables, when  system (2) is chaotic.
system (2) is chaotic.
Chen system is described by
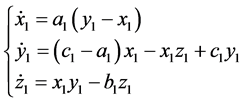 (3)
(3)
When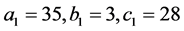 , system (3) is chaotic.
, system (3) is chaotic.
In the next section, we will study chaos anti-synchronization between Chen and Genesio systems with known or unknown parameters using adaptive control.
3. Adaptive Anti-Synchronization between Chen and Genesio System with Unknown Parameters
We assume that Genesio system (2) is the drive system, and the controlled Chen system (4) is the response system.
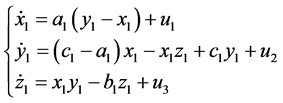 (4)
(4)
We add (2) from Equation (4) and yield
![]() (5)
(5)
Our goal is to find the proper controllers ![]()
![]() and parameter update laws, such that system (4) globally anti-synchronizes system (2) asymptotically. i.e.
and parameter update laws, such that system (4) globally anti-synchronizes system (2) asymptotically. i.e.
![]()
where![]() .
.
Theorem: If the controllers are chosen as
![]() (6)
(6)
and the update laws of parameters are chosen as
![]() (7)
(7)
Then system (4) globally anti-synchronizes system (2) asymptotically, where ![]() are positive constants,
are positive constants, ![]() are estimate values of
are estimate values of![]() , respectively.
, respectively.
Proof: Applying control laws (6) to (5) yields the resulting error dynamics as follows.
![]() (8)
(8)
where ![]()
![]() .
.
Consider the following Lyapunov function
![]()
The time derivative of V along the solution of error dynamical system (8) gives that
![]()
where ![]()
Since ![]() is positive definite and
is positive definite and ![]() is negative semi-definite in the neighborhood of zero solution of system (5), it follows that
is negative semi-definite in the neighborhood of zero solution of system (5), it follows that ![]()
![]() and
and ![]() from (8), we have
from (8), we have ![]() since
since![]() , we obtain
, we obtain
![]()
where ![]() is the minimal eigenvalue of the positive definite matrix P. Thus,
is the minimal eigenvalue of the positive definite matrix P. Thus, ![]() by Barbalat’s lemma, we have
by Barbalat’s lemma, we have ![]() Therefore, response system (4) can globally anti-synchronize drive system (2) asymptotically. This completes the proof.
Therefore, response system (4) can globally anti-synchronize drive system (2) asymptotically. This completes the proof.
In simulation, Fourth order Runge-Kutta integration method is used to solve the systems of differential Equations (2) and (4) with the controllers (6) and the parameter update laws (7). We select the parameters of Genesio system as ![]() and the parameters of Chen system as
and the parameters of Chen system as ![]() respectively, and
respectively, and ![]() The initial values of drive and response systems are
The initial values of drive and response systems are ![]()
![]() and
and ![]() respectively, while the initial errors of system (5) are
respectively, while the initial errors of system (5) are ![]() and the initial values of estimate parameters are
and the initial values of estimate parameters are![]() ,
,
![]() The anti-synchronization errors between Chen system and Genesio system are shown in Figure 1, the estimate values of parameters
The anti-synchronization errors between Chen system and Genesio system are shown in Figure 1, the estimate values of parameters ![]() and
and ![]() are shown in Figure 2 and Figure 3, respectively. Obviously, the anti-synchronization errors converge asymptotically to zero and two different systems are indeed achieved chaos anti-synchronization. Furthermore, the estimates of parameter converge to their true values.
are shown in Figure 2 and Figure 3, respectively. Obviously, the anti-synchronization errors converge asymptotically to zero and two different systems are indeed achieved chaos anti-synchronization. Furthermore, the estimates of parameter converge to their true values.
![]()
Figure 1. Anti-synchronization errors between Chen and Genesio systems via adaptive control.
![]()
Figure 2. Estimate values of parameters a, b, c of drive system.
![]()
Figure 3. Estimate values of parameters a1, b1, c1 of response system.
4. Conclusion
In this paper, chaos anti-synchronization between two different chaotic systems with different structures using adaptive control is presented. Chen system and Genesio system are taken as an illustrative example to verify the effectiveness of the proposed methods.