Received 27 June 2016; accepted 8 July 2016; published 29 July 2016

1. Introduction
In order to help students to be prepared for modern physics, many professors ask students to forget what they learn in classical physics. If a student ask too many questions based on what they learn in classical physics, it will be difficult for any professor to have progress in teaching modern physics. Even though, Einstein already demonstrated that time and space are related from the thought experiment by emitting photons from the middle of a car of the moving train, we still treat them as independent in a 4-d-s-t frames. In 4-d s-t frame, the representation of 3 dimensions of (x, y, and z) and dimension of time (t) are all perpendicular each other. The only way to depict this is to have three separate graphs of x vs. t, y vs. t, and z vs. t with time which can be negative on those graphs. Later, Minkoski added the same constraint for a pair of inertial frames to make time and space related in the following equation.
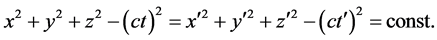 (1)
(1)
We believe that time and spaces are dependent and should be shown in a frame which is applied not only to modern physics but also to classical physics. A 3-d s-t frame serves that purpose. We can draw the time dilation and length contraction between two inertial 3-d s-t frames. We can show that a 4-d s-t frame is the approximation of a 3-d s-t frame, when the velocity of a moving frame is much less than the velocity of the medium. We also show that a 3-d s-t frame is equivalent to a 4-d s-t frame after properly converting coordinates between two frames.
2. Time Dilation Shown in 3-d s-t Frames
There is a pair of inertial frames [1] : The 3-d s-t frame O’ travels at the velocity u with respect to the 3-d s-t frame O. We can assume that the frame O is constructed in the platform and the frame O’ is constructed in the train traveling along the railroad. The radius of the sphere at t is  for the frame O and the radius of the sphere at
for the frame O and the radius of the sphere at 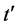 is
is 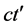 for the frame O' where c is the velocity of the medium. The motion of the train is a vertical line described from the frame O' and is a slanted line described from the frame O in Figure 1(a).
for the frame O' where c is the velocity of the medium. The motion of the train is a vertical line described from the frame O' and is a slanted line described from the frame O in Figure 1(a).
Because of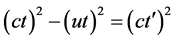 , then we are able to derive
, then we are able to derive
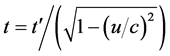 (2)
(2)
which is called time dilation [2] . The time, t', recorded from the event of the train moving along the railroad in the frame O' is called proper(original) time, because the train comes into contact with the track in front at the same location (head of the train) viewed from the frame O'. The time recorded from the event of the train moving along the railroad in the frame O is called special time, because the train comes into contact with the tract in front at different locations (different parts of the tract), as viewed from the frame O.
The special time for measuring an event happened at the different locations in the 3-d s-t frame O is always longer than the proper time for measuring an event that happens at the same location in the 3-d s-t frame O'. In modern physics, it is called time dilation. We are able use the same graph to derive length contraction formula.
Because of 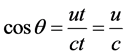 and
and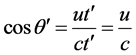 , then
, then
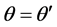 . (3)
. (3)
Because of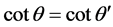 , then
, then 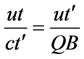 where
where
![]()
![]() (a) (b)
(a) (b)
Figure 1. (a) Red circles represent the polar coordinates on the platform. We are able to construct a new space-time frame by presenting time with polar coordinates on the platform to describe the motion of the train using the line OA. (b) Blue circles represent the polar coordinate on the train. We are able to construct a new space-time frame by presenting time with polar coordinate on the train to describe the motion of the platform using the line O'B.
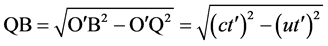 . (4)
. (4)
The motion of the frame O' is described as the slanted line OA from the frame O and the motion of the frame O is described as the slanted line OB from the frame O' in Figure 1(b).
Because of 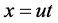 and
and![]() , then the above equation can be expressed as
, then the above equation can be expressed as
![]() (5)
(5)
then it can be expressed as
![]() (6)
(6)
which is called length contraction [2] . If we want to measure the length of any object, we can lay the object along the railroad. Now, let us assume that there is a rod, which can be extended to the length of![]() , is laid alongside the station platform. There is an observer O on the platform and another observer O' on the train and both measure the rod’s length using a sensor attached to the front of the train, i.e. the origin O' of the moving frame S'. The length of the rod as measured by an observer on the stationary frame S with respect to the rod, is defined as proper (original) length, x, while the length of the rod as measured by an observer on the moving frame S' with respect to the rod, is defined as special length,
, is laid alongside the station platform. There is an observer O on the platform and another observer O' on the train and both measure the rod’s length using a sensor attached to the front of the train, i.e. the origin O' of the moving frame S'. The length of the rod as measured by an observer on the stationary frame S with respect to the rod, is defined as proper (original) length, x, while the length of the rod as measured by an observer on the moving frame S' with respect to the rod, is defined as special length,![]() . This equation shows that the special length,
. This equation shows that the special length, ![]() , is always less than the proper length, x. This result states that the length of a rod as measured by an observer in a moving frame is shorter than the one measured by an observer on a stationary frame.
, is always less than the proper length, x. This result states that the length of a rod as measured by an observer in a moving frame is shorter than the one measured by an observer on a stationary frame.
3. Approximately Absolute Time Can Be Shown in 3-d s-t Frames
For a pair of inertial 3-d s-time frames, if the velocity of moving frame is much less than the velocity of medium, then time is approximately same for both frames shown in the following graph Figure 2(a). If![]() , then
, then ![]() and
and ![]() from the formula of time dilation
from the formula of time dilation
![]() . (7)
. (7)
From the figure of Figure 2(a), if![]() , then
, then ![]() where r is the hypotenuse and h is the height of the right triangle. Dived c on both sides, then
where r is the hypotenuse and h is the height of the right triangle. Dived c on both sides, then ![]() where
where![]() ,
, ![]() and
and
![]() . (8)
. (8)
From 3-d s-t frames, we can understand why time can be treated as absolute value regardless frame i in classic physics, where u << c, regardless of the frame of reference.
Figures 2(a)-2(d) show the motion of moving train at different percentage velocity of the medium with wave property.
4. Converting between Coordinates of a 4-d s-t Frame and Coordinates of a 3-d s-t Frame
The coordinates of a particle in the 4-d s-t frame are![]() . The coordinates of a particle in the 3-d s-t frame are
. The coordinates of a particle in the 3-d s-t frame are![]() . Converting between a 4-d s-t frame and a 3-d s-t frame is following:
. Converting between a 4-d s-t frame and a 3-d s-t frame is following:![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() , the velocity of a medium with property of wave (light, sound,…), where T is period
, the velocity of a medium with property of wave (light, sound,…), where T is period
of the wave, ![]() is the wavelength of the wave (see Figure 3).
is the wavelength of the wave (see Figure 3).
If the unit of time is sec, then the unit of radius for polar circle is chosen to be the period of the wave-medium, then the unit of x-axis should be chosen as the wavelength of the wave. We construct this new space-time frame to make space and time dependent by using the period and the wavelength of the wave-medium. Furthermore,
the ratio of wavelength to period is equal to the velocity of the wave-medium,![]() .
.
In order to describe the motion of an object in 3-dimensional space along the locations of x-axis, y-axis, and z-axis, we can construct a new space-time frame. Spheres with different radius representing different outgoing time, polar coordinates will be formed from circles of intersections between spheres and x-y plane, y-z plane, and z-x plane [3] . We are able to use the red polar coordinates of x-y plane, the blue polar coordinates of y-z plane, and the gray polar coordinates of z-x plane to describe the locations of a moving object moving along x-axis, y-axis, and z-axis in Figure 4. This kind of new coordinate frame, which embeds the time axis into space axes is called 3-d s-t frame. This new coordinate frame eliminates one dimension from the 4-d s-t frame and solves the puzzle of visualizing a time axis which perpendicular to 3 already perpendicular spacial dimensions.
5. Equivalence between a 4-d s-t Frame and a 3-d s-t Frame
In the following section, we try to find relations between kinetic terms in a 4-d s-t frame and kinetic terms in a 3-d s-t frame through:![]() ;
;![]() ;
;![]() ;
;![]() ;
; ![]() where T is the period of wave and λ is the wavelength of wave. We also try to find the forms of dynamic formula in a 3-d s-t frame through the same conversion.
where T is the period of wave and λ is the wavelength of wave. We also try to find the forms of dynamic formula in a 3-d s-t frame through the same conversion.
![]() (9)
(9)
![]()
Figure 3. Constructing a new space-time frame by presenting time with unit of T and length with unit of l using polar coordinates.
![]()
Figure 4. Three-dimensional space-time frame formed by three polar planes on three different planes.
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
Distance of a particle with a constant velocity
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
Distance of a particle with a constant acceleration
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() . (38)
. (38)
It shows that all kinetic formulas in a 3-d s-t frame are same as in classical physics.
Newton’s Second Law:
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
and
![]() . (42)
. (42)
Momentum:
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
and
![]() . (46)
. (46)
Kinetic Energy:
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
and
![]() . (50)
. (50)
The other form of Newton’s Second Law:
![]() (51)
(51)
![]() (52)
(52)
![]() . (53)
. (53)
It shows that the all forms of dynamic formula in a 3-d s-t frame are same forms of dynamic formula in classical physics.
a) In Modern Physics:
For time dilation
![]() (54)
(54)
![]() (55)
(55)
![]() . (56)
. (56)
For length contraction
![]() (57)
(57)
![]() (58)
(58)
![]() . (59)
. (59)
It shows that the all forms of kinetic formula in a 3-d s-t frame are same forms of kinetic formula in modern physics.
6. Discussion
This paper expounds that a 4-d s-t frame is the approximation of a 3-d s-t frame, when the velocity of a moving frame is much less than the velocity of the medium. While, showing the equivalence between a 4-d s-t frame and a 3-d s-t frame by proper converting coordinates of two frames. In the “Time Dilation and Length Contraction Shown in Three-Dimensional Space-Time Frames”, demonstrates that we are able to visualize time dilations and length contractions through graphs on Figure 1(a) and Figure 1(b) when 3-d s-t frames are used to describe motions of particles moving at high velocity which is percentage of the velocity of light.
We are able to describe the motion of a particle at very small velocity, relative to the velocity of light in a 3-d s-t frame in classical physics. The following graph (see Figure 5) illustrates how to utilize this new 3-d s-t Frame to describe the motion of particles moving along the x-axis with different velocities [2] . If the velocity of sound, which is the medium of the system, is Vm = 343 m/sec, then the radius of the circle representing 1sec would be
![]() (60)
(60)
the radius of the circle representing 2 secs would be
![]() (61)
(61)
etc. In Figure 5, we use different lines OA, OB, OC, OD, OE, FG to describe the different motions of particles which velocities are much less than Vm = 343 m/sec, the velocity of sound which is the medium of the system.
We also able use the velocity of sound
![]() (62)
(62)
to construct a polar coordinate by letting ![]() and
and ![]() to describe motions of particles of the system.
to describe motions of particles of the system.
P.S.: For all figures except Figure 5 in the paper, there are numbers along x, y, z axes. The purpose of these numbers aids drawing from the MATLAB program of the computer.
![]()
Figure 5. OA represents a particle that remains stationary at O, OB represents a particle moving with a relatively slow constant velocity, OC represents a particle moving with a relatively fast constant velocity, OD represents a particle moving with a constant acceleration, OE represents a particle moving with a constant deceleration, and FG represents a particle that remains stationary at F.
![]()
Figure 6.A single particle moving in a helix in space: A particle moves in circles on the x-y plane while also moving with constant speed along the z-axis.
It might be worth to discuss rewriting textbooks of classical physics and modern physics described in 3-d s-t frames for teaching physics [4] .
We believe that if students study physics using 3-d s-t frames, they will benefit by this approach [5] .
7. Conclusion
A 4-d s-t frame is independent and is only tied together using an equation constraint. A 3-d s-t frame is dependent and the constraint is embedded into the system [6] . A 3-d s-t frame can represent both time dilation and length contraction in graphs. In 3-d s-t frames, one important distinction between space and time is that space is bidirectional and time is unidirectional, i.e. an object can proceed forward and backward in space but can only proceed forward in time. In the proposed 3-d s-t frame, the representation of time as concentric spheres of different radii centered about the origin of the spatial axes inherently restricts time to a single direction, i.e. negative time (circles with negative radii) has no meaning. Essentially, a 4-d s-t frame and a 3-d s-t frame can be considered as equal by proper converting coordinates of two frames, because their forms of laws of physics are equivalent. Thus, a 3-d s-t frame can serve as a bridge connecting classical physics and modern physics.